用似然比法则导出威尔克斯分布
2016-09-15江忠伟
江忠伟
(兰州财经大学,甘肃 兰州 730020)
用似然比法则导出威尔克斯分布
江忠伟
(兰州财经大学,甘肃兰州730020)
在多元统计分析中需要一些性质优良的抽样分布来进行统计推断.本文首先从不同角度研究多元正态分布,在多元统计分析中,我们以多元方差分析为背景,通过对一元方差分析所构建的F统计量进行推广,引出我们想要研究的统计量.
多元正态分布;似然比统计量;多元方差分析;威尔克斯分布
1 背景
多维随机现象是十分复杂的,必须使用科学的方法进行研究.一个很自然的想法是以多元正态分布为基础衍生出类似一元统计分析中的似的三大分布,我们以三大分布为基石进行更加细致的研究,解决现实问题.很多经典多元统计分析的教材中都介绍由多元正态分布衍生出的三大分布,但是介绍得不够详细,没有给出具体的背景,仅仅给出一个定义,这对我们理解它们以及进行更深入的研究是不利的.本文首先从不同角度定义多元正态分布,接着介绍矩阵正态分布,最后由一元方差分析推广到多元方差分析为背景,引出了威尔克斯分布.
2 多元正态分布的三种定义
2.1横向推广法
一元正态分布中,若Y~N(0,1),则X=μ+δY~N*μ,δ2).利用这种思想我们可以定义多元正态分布.
设y=(y1,…yq),y1,…yq独立同分布N(0,1),μ为p维常数向量,A为p行q列的常数矩阵,则称x=μ+A'y的分布为多元正太分布.
2.2特征函数法
上面的定义仅仅描述了多元正态分布,我们需要研究多元正太分布的相关性质.需要像一元正态分布那样给出具体的密度函数.由独立同分布的性质及2.1得:

由y=(A')-1(x-μ)、(1)式、雅可比变换可得:

其中∑=A'A,这里我们要求∑>0.为了把多元正态分布推广到更一般的情形,即推广到协方差矩阵∑是非负定的情形∑≥0,可以用特征函数代替分布函数.
设Y~N(0,1),Y的特征函数g(t)为:

若X=μ+δY~N(μ,δ2),则相应的特征函数为:

同理,多元正态分布的特征函数也可以做类似的推广. 设y=(y1,…,yq),y1,…yq独立并且服从标准正态分布.对任意的向量t=(t1,…,tq),由独立同分布的性质知:

平行推广,若x=μ+A'y,μ为p维常数向量,A为p行q列的常数矩阵.则:

综上,得出了多元正态分布的特征函数,显然(2)式只与μ、A'A有关,可以令A'A=∑,用x~Np(μ,∑)表示满足(2)的x服从多元正态分布.
2.3线性组合法
设x是p维随机向量,若x的任一线性组合a'x(a∈Rp)都是一元正态分布,则我们可以说x服从多元正太分布.下面证明这一结论.
证明a'x(a∈Rp)服从一元正态分布,则它的各阶矩都存在.令μ=ε(x),∑=D(x),于是:E(a'x)=a'μ,V AR(a'x)=a'∑a,
又因为a'x~N(a'μ,a'∑a),a'x的特征函数为:

取θ=1,则

(3)式的右边恰好与上面2.2的(2)的右边一样,所以2.2与2.3可以看成是等价的.即x~Np(μ,∑).
3 多元正态分布似然函数的极值问题
3.1矩阵正态分布
若矩阵的各个元素均服从标准正态分布,称该矩阵为矩阵正态分布.类似的,我们可以采取上面多元正态分布定义2.1将矩阵正态分布推广到一般的情形.
若BB'>0,AA'>0,W=BB',V=AA'则有密度函数:

3.2多元正态分布似然函数的极值问题
若我们从Np(μ,∑)抽取n个独立样本.这n个样本可以组成矩阵X,X服从矩阵正态分布.我们求多元正态分布似然函数的极值问题,转换成求矩阵正态分布密度函数的极大值).由上面的(4)知X的密度函数为,

于是,

当且仅当μ=x,等式成立.所以,

当n>P时,P(A>0)=1,此时有非退化随机阵C,使A=CC'.

最终得出极大值为:
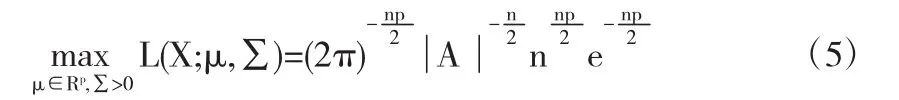
4 威尔克斯分布
若正态总体是多元正态总体,设有k个总体G1,…,Gk,从这k个总体独立抽取样本为:

xjα,α=1,…,k;j=1,…,nα相互对立,要检验:
H0:μ1=…=μk,H1:存在i≠j,使μi≠μj.
多元方差分析需要构建什么样的检验统计量,一个很自然的想法是将一元方差分析中的检验统计量F统计量进行推广.F统计量的组间方差、组内方差推广后成为组间离差阵、组内离差阵.我们需要解决两个问题,第一,怎样导出检验统计量;第二,推广后的统计量服从什么分布.
首先,解决第一个问题.这里采取似然比法则导出统计量.组间离差矩阵、组内离差矩阵、组内离差矩阵分别为:

易见T=B+E.似然比统计量为:

前面介绍过多元正态分布似然函数的极值问题,
类似上式(5),可以求得极大值:

因此似然比统计量:

接下来,回答第二个问题.我们称形如(6)统计量成为威尔克斯统计量.下面给出更一般的定义:设A~Wp(n,∑)和B~Wp(m,∑)相互独立,n>p,m>p则称:服从威尔克斯分布,记作:Λ~Λp,n,m.

5 总结
5.1进行多元方差分析时,需要导出检验统计量,由一元方差分析的检验统计量推广到多元,研究推广后的统计量,得出该统计量服从威尔克斯分布.
5.2威尔克斯分布同F分布一样要求分子分母是独立的,证明方法很多.我们可以构建投影阵,利用推广后的科克朗定理很容易证明E和T是独立的.
5.3从多元正态分布中抽取样本时,要求样本容量n大于p,如果n小于p,我们如何克服这个问题?
〔1〕傅德印,张旭东.EXCFL与多元统计分析[M].北京:中国统计出版社,2007.
〔2〕方开泰.实用多元统计分析[M].上海:华东师范大学出版社,1989.
〔3〕茆诗松,王静龙,濮晓龙.高等数理统计[M].北京:高等教育出版社,2006.
O212.1
A
1673-260X(2016)08-0009-02
2016-04-11
