关于极坐标系下二重积分的计算法的教学设计探讨
2016-09-15杨星星
杨星星,宁 群
(宿州学院 数学与统计学院,安徽 宿州 235000)
关于极坐标系下二重积分的计算法的教学设计探讨
杨星星,宁群
(宿州学院数学与统计学院,安徽宿州235000)
课堂教学设计是提高课堂教学效率的前提和重要保证,是课堂教学成功的关键.数学教学过程是一个传授数学思想和方法的过程,二重积分的计算是多元积分学的核心,这部分内容蕴涵着丰富的数学思想和数学方法,是值得探讨和研究的部分.
二重积分;计算;教学设计
利用极坐标计算二重积分的教学设计面向工科专业学生,他们在部分专业课程的学习中要用到高等数学知识.如材料化学专业学生在学习“材料科学基础”、测绘工程专业学生在学习“流体力学”、计算机科学与技术专业学生在学习“数字信号处理”时都要用到二重积分的知识.
1 教材分析
二重积分既是定积分的推广,又为后面系统地学习三重积分、曲线积分和曲面积分提供研究和学习的方法,是多元积分学的基础.二重积分计算的主要思路是转化为两次定积分即二次积分,当被积函数和积分区域在极坐标系下表示比较方便时利用极坐标计算往往会化繁为易.
2 学情分析
学生已经学习了一元函数的微积分;已经掌握了在直角坐标系下二重积分的计算;但学生情况制约着学习的开展,影响着目标的达成,学习不仅受学生原有知识基础的制约,而且还受学生的认知风格、能力状况和学习兴趣等影响.
3 教学目标
3.1知识目标
(1)掌握二重积分在极坐标系下的表达式;
(2)掌握极坐标系下二重积分化二次积分的方法.
3.2能力目标
(1)理解二重积分从直角坐标到极坐标的换元思想;(2)理解在极坐标系下二重积分化二次积分的思想方法和具体过程,能够熟练应用.
3.3素质目标
(1)通过教师的提示和启发,培养学生深入思考、积极发言的良好习惯,加强语言表达能力;
(2)引导学生注重数学思想方法的学习,树立“学数学是为了用数学”的意识.
4 教学策略与设计思路
4.1教学方法
(1)为突出重点,采取类比分析、实例分析,使学生主动参与提出问题与解决问题的过程,充分发挥学生的主体作用.
(2)为突破难点,采取演示、讲授、启发等方式,充分发挥教师的主导作用.
4.2教学手段
除使用常规的教学手段外,还将使用多媒体投影和计算机来辅助教学,目的是充分发挥其快捷、生动、形象的特点,为学生提供直观感性的材料,有助于学生对问题的理解和认识,在优化组合的基础上,提高教学效率,改善教学效果.
4.3设计思路
对一个计算二重积分的问题,可以考虑应用前面学过的直角坐标系下的求解方法但由于被积函数较复杂,但在极坐标系下表达式简单,转化到极坐标系下求解.由而引发思考:极坐标系下二重积分的表达式?极坐标系下积分变量的取值范围?类比分析,由浅入深,逐步探索,得到确定极坐标变量上下限方法:三线法.应用此方法,很方便就能求出开始给出的二重积分的解,学生自己动手,增加成就感.联系实例,深入探究,解决问题.归纳小结,给出极坐标系下二重积分计算的具体步骤,提高认识,最后适当练习,巩固新课.结构完整,条理清晰.
5 教学过程
5.1引入
前面我们已经学习了二重积分在直角坐标系下的计算,利用直角坐标进行将二重积分转化为二次积分的过程中,关键是选择积分区域的类型X-型或Y-型也即是确定了积分的次序,这个过程中不但要考虑积分区域的形状还有考虑被积函数的特性.下面我们来求这个二重积分

图1
根据直角坐标系下二重积分的计算步骤:首先画出积分区域的图形(PP T显示),积分区域关于x轴、y轴对称且被积函数关于x、y都是偶函数,由对称性,记第一象限的积分区域为
然后选择积分次序,但是无论先积x还是先积y,这个被积函数的原函数都不易求得.由于被积函数和积分区域的边界曲线方程中都含有x2+y2,想到转化为极坐标系下求解.
5.2极坐标系下二重积分的表达式
利用直角坐标和极坐标变量之间的转换关系:x r=c o sθ,y=rs inθ可以将被积函数f(x,y)转化为f(r c onθ,rs inθ),直角坐标系下的面积元素d x d y转化为r d r dθ,积分区域D的边界曲线方程转化为极坐标变量表示.这样我们就得到了极坐标系下二重积分的表达式这样就把积分变量转换成了r和θ,其换元思想类似于定积分的换元法.
5.3极坐标系下二重积分化为二次积分
极坐标系下二重积分的表达式已经知道,怎样确定极坐标变量r和θ的范围就成了将其化为二次积分的关键了.在极坐标系下有界闭区域D如图2:
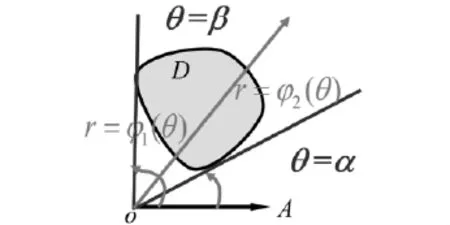
图2
如果积分区域D介于两条射线θ=α,θ=β之间,从极点出发在区间(α,β)上任意作一条极角为θ的射线穿过区域D的内部先交曲线r=φ1(θ)后交r=φ2(θ)即D内任一点(r,θ),其极径总是介于曲线r=φ1(θ),r=φ2(θ)之间.
则区域D的积分限
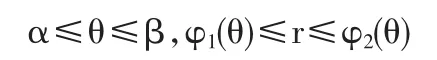
于是

称上述确定r和θ上下限的方法为三线法.
(2)利用这个方法来求先前遇到的思考题,把二重积分转化为极坐标系下
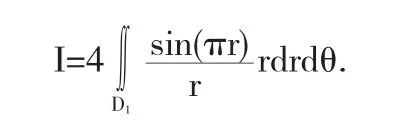
(3)实例分析[1]:求球体 x2+y2+x2≤4a2被圆柱面x2+y2=2a x(a>0)所截得的(含在圆柱面内的部分)立体的体积如图3.
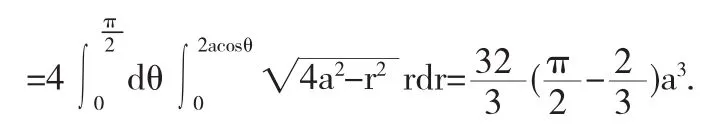

图3

图4
5.4极坐标系下计算二重积分的具体步骤
5.5利用极坐标计算二重积分的范围[2]
如果积分区域是圆、半圆、圆环、扇形区域等情况下且被积函数是)形式,利用极坐标来计算往往会简
便很多.
5.6课后思考,小组协作
6 教学反思
(1)教学大纲要求我们在教学过程中要着重培养学生的探究、发现、创新等方面的能力.学习的全过程需要学生的参与,学生是学习的主体和中心.围绕这个宗旨,我在课堂内容的编排和教学课件的制作上作了一定的思考.在内容编排上,我基本遵循由易到难的过程,从最基本的,学生所熟知的前课知识开始引入,由浅入深的引导学生加以足够地探究,使学生的发现变得自然而水到渠成.同时对于学生可能的探究结果留有足够的空间,充分肯定学生的创新发现,对于学生考虑不到的地方加以补充、引导、完善,并留出一定课后思考得余地.在课件制作方面,考虑到多媒体直观形象的特点,让其承担起引导思考与解释的重任. (2)这节课还有一些不足之处,课堂容量过大,导致了省略定积分具体计算过程的遗憾.课件的制作也达不到特别美观的要求,不能更好的发挥其应有的作用.在今后的教学中我会不断的完善自己的教学技能,提高自己的业务水平,做到能灵活把握教材,详略处理得当.正确处理教与学的关系,努力体现一种流畅的教学风格[4].既充分发挥学生的主观能动性,又不完全以学生为中心,做到教与学的良好互动.
〔1〕同济大学数学系.高等数学[M].北京:高等教育出版社,2007.
〔2〕连坡.高等数学课堂教学的思考与探索[J].高等数学研究,2011,2(14):45-46.
〔3〕贾红艳.大学数学教学方法的几点思考[J].教育与教学研究,2010,2(24):99-100.
〔4〕杨宏林,丁占文,田立新.关于高等数学课程教学改革的几点思考[J].数学教育学报,2004,2(13):74-76.
O172.2
A
1673-260X(2016)08-0004-03
2016-04-26
宿州学院2015质量工程项目(201510379083)
