单电磁悬浮系统的神经网络模糊滑模控制*

刘春芳， 胡雨薇

(沈阳工业大学 电气工程学院， 沈阳 110870)



单电磁悬浮系统的神经网络模糊滑模控制*

刘春芳， 胡雨薇

(沈阳工业大学 电气工程学院， 沈阳 110870)

为实现单电磁悬浮系统悬浮气隙的精确控制，提出一种基于神经网络的模糊滑模控制方案.根据单电磁悬浮系统的动态非线性数学模型，设计使系统状态在有限时间内到达稳定点的滑模面，同时根据滑模切换状态，通过引入神经网络的模糊控制方法对滑模切换控制量的增益进行评估，实时对滑模控制量进行调整，实现切换控制信号的柔化.基于神经网络的模糊滑模控制系统不仅能很好地跟踪给定信号，而且能削弱滑模控制抖振，对外部扰动具有完全的鲁棒性.仿真结果表明，所设计的控制系统零超调，具有速度跟踪性能，对外部扰动具有很强的鲁棒性.

磁悬浮技术； 单电磁悬浮系统； 滑模控制； 模糊推理； 鲁棒性； 零超调； 神经网络； 非线性控制

磁悬浮技术是一个涉及电磁学、控制理论、机械学以及计算机科学等多个学科的高新技术，是利用磁场力的支撑实现悬浮体无机械接触的悬浮，消除机械结构之间的接触[1].由于磁悬浮技术从根本上改变了传统的支撑模式，具有传统技术无法比拟的优越性，所以其研究和开发都处于快速发展之中[2].但磁悬浮系统是开环不稳定且高度非线性的系统，对磁悬浮系统实施有效的控制是磁悬浮技术应用需要解决的关键问题，因此，研究磁悬浮系统的控制算法具有重要意义.大多数关于磁悬浮系统的理论研究都基于线性理论，依据线性化后的数学模型设计磁悬浮控制器[3].但磁悬浮系统是开环不稳定、高度非线性的系统[4]，如何选择有效的控制方案，使受控的磁悬浮系统达到精确的控制要求，抑制ra扰动是研究的重要课题[5-8].本文针对该问题设计了神经网络的模糊滑模控制器.滑模控制是一种非连续控制，由于滑动模态可以进行设计且与对象参数及扰动无关，使其具有良好的鲁棒性，但同时也因为高频率的切换产生了严重的抖振现象[9].针对该问题将模糊控制和滑模控制相结合，既保留了传统滑模控制的优点，又利用了模糊控制改变滑模控制中切换控制量的特点，从而实现了使抖振减小的目的.模糊控制是一种仿人思维的控制技术，需要专家的先验知识进行近似推理，缺乏在线自学习和在线自调整的能力.针对这一问题，本文利用神经网络对环境变化有极强自学能力的特点，从而不断完善模糊控制中的经验和规则库，得到更为精确的切换控制量.

1　单电磁铁悬浮系统数学模型

图1为单电磁铁的悬浮结构.假设忽略漏磁通和铁磁阻以及导轨的磁阻，推导磁悬浮系统的动态数学模型[10-11].

图1　单电磁铁悬浮系统结构

单磁铁的数学模型为

(1)

(2)

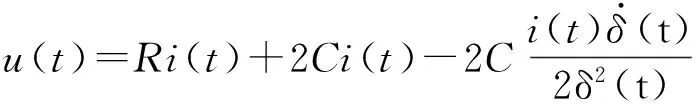
(3)

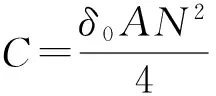
(4)

式中：δ(t)为悬浮间隙；F(i，δ)为电磁吸力；m为悬浮平台的质量；fd(t)为干扰；i(t)为控制线圈电流；u(t)为控制线圈两端电压；R为电阻；A为铁芯面积；N为电磁铁绕组匝数；δ0为平衡点悬浮高度.

2　系统控制器设计

2.1滑模控制器设计

在滑模控制策略中，滑模控制律是由等效控制ueq和切换控制usw构成，等效控制保证系统的状态在滑模面上，切换控制保证系统的状态不离开滑模面.

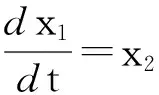
(5)

(6)

(7)

令系统的输出为y=z1=x1-x1d，设计滑模控制器的滑模面为

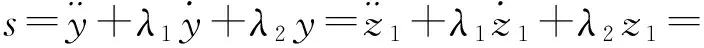
z3+λ1z2+λ2z1

(8)

式中，λ1和λ2为设计滑模面固定公式中的常数项.将z1、z2、z3代入式(8)，滑模面为

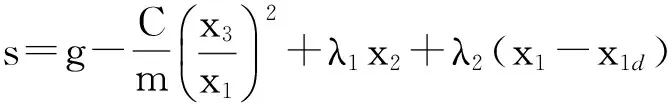
(9)

由式(8)、(9)可以得出，当系统进入滑模面后，所选取的滑模面保证了在t→∞时，y=z1=x1-x1d收敛于0(s=0)，则有

(10)

式中，W为常数增益.

滑模控制器的控制律为

u=ueq+usw=

(11)

2.2神经网络的模糊滑模控制器设计

本文控制方案的出发点是在不破坏滑模成立条件下，尽量减少滑模控制中切换控制的增益W，从而削弱控制系统的平均抖动.综上分析，可得到基于神经网络的模糊滑模控制策略的单电磁悬浮系统框图，如图2所示.

图2　单电磁悬浮系统原理框图

Mamdani型模糊系统采用后件和前件之间通过最小算子或t-范数联接的推理方法，其定义为

(12)

输出的模糊集合B′⊆Y，其定义为

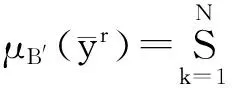
(13)

最后将输出的模糊值采用重心法清晰化，即

(14)

式中，agr()为映射的集合.

2.2.1神经网络权系数的调整

切换控制系统为双输入、单输出的Mamdani型神经网络模糊系统.采用单点模糊化乘积推理和重心法清晰化得到模糊系统的输出，神经网络模糊系统结构如图3所示.

图3　神经网络模糊系统结构

第三层：完成模糊推理过程中规则的后件，最终输出模糊量.

第四层：采用重心法，将得出的模糊量转换成清晰量，最终得到切换控制律usw.

本文采用两种方式来训练.为了加快学习，可先用先验知识对该系统进行离线训练，然后再进行在线学习.

定义训练模糊神经网络的误差函数为

(15)

2.2.2输出层权系数的调整

权系数按J函数梯度变化的反方向调整，使网络逐渐收敛.根据梯度法，可得输出层每个神经元权系数的修正公式为

(16)

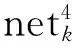
(17)

(18)

隐含层权系数的调整与输出层权系数的调整过程相同，同样采用梯度下降法，整理得出隐含层任意神经元i的加权系数修正公式，即

(19)

3　仿真结果与分析

为了实现数控机床高加工精度的要求，所设计的模糊滑模控制器能够使工作平台稳定地悬浮在2mm处，并在有扰动影响的情况下具有完全的自适应性和强鲁棒性.根据前文所设计的控制器，利用MATLAB/Simulink进行仿真.系统参数见表1.

表1　系统参数

图4为滑模控制系统悬浮气隙输出曲线.当给定信号为幅值为1 mm，周期为2 s的正弦信号时，滑模控制系统能够较好地跟踪给定的正弦信号，但输出曲线出现很大的抖动.

图4　滑模控制系统悬浮气隙输出曲线

图5为神经网络的模糊滑模控制系统.从图5中看出，该控制系统不仅能够较好地跟踪给定信号，并且相对于滑模控制抖动很小.

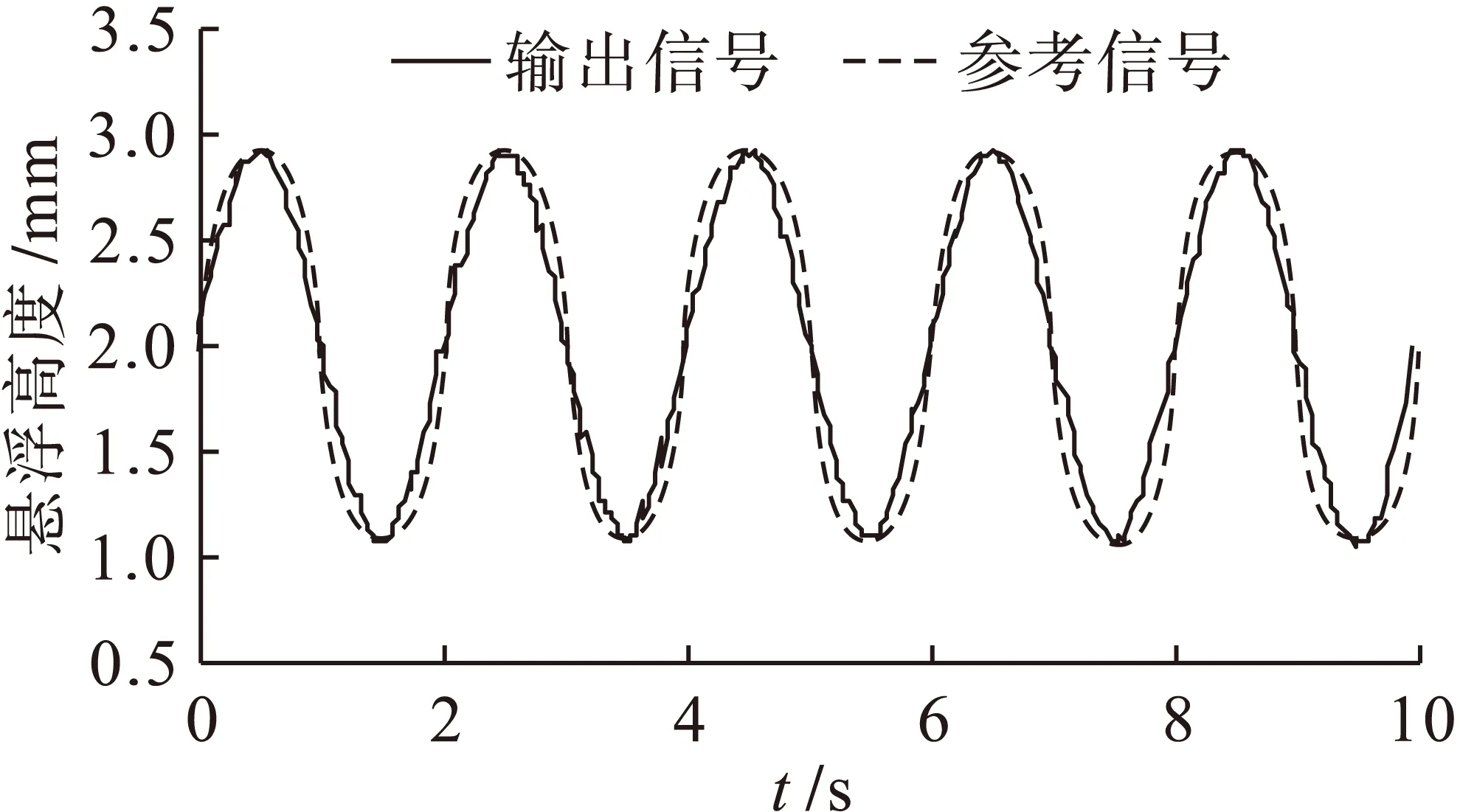
图5　模糊滑模控制系统悬浮气隙输出曲线

图6为滑模控制系统的跟踪误差曲线.滑模控制虽然能较好地跟踪给定正弦信号，但由于滑模控制本身带来抖振的原因，导致在跟踪曲线的过程中出现了很大的跟踪误差.

图6　滑模控制系统跟踪误差曲线

图7为神经网络的模糊滑模控制系统的跟踪误差曲线.与图6相比，相对于滑模控制，神经网络模糊滑模控制系统不仅跟踪效果好，而且跟踪过程中跟踪误差很小.

图7　模糊滑模控制系统跟踪误差曲线

图8为滑模控制系统的控制律的正弦响应输出曲线.由图8可知，当给定信号为正弦信号时，滑模控制系统的控制律输出曲线出现明显的抖动.

图9为神经网络的模糊滑模控制系统控制律的正弦响应输出曲线，与图8相比，当在滑模控制中加入神经网络模糊控制策略后，明显削弱了滑模控制本身所带来的抖动.

图9　模糊滑模控制系统的控制律输出曲线

为了使系统具有良好的性能，要求所设计的系统必须具有快速性、稳定性和无超调量的优点.除此之外，控制系统不仅需要满足磁悬浮系统对快速性和稳定性的静态性能的要求，还要考虑系统的动态性能，即当系统某一时刻受到扰动时，能够快速回调并重新稳定在期望值.

为了得到滑模控制和神经网络模糊滑模控制快速性和稳定性的比较，将给定信号变为阶跃信号，期望悬浮高度为2 mm，并且系统在0.6 s时，受到竖直扰动力2 000 N.图10为加入扰动后，滑模控制系统及神经网络的模糊滑模控制系统悬浮气隙响应曲线.

由图10可以看出，神经网络的模糊滑模控制系统的响应速度及稳定性比滑模控制系统好.在达到平衡位置后，滑模系统的输出曲线仍不稳定，出现抖动的情况.当系统在0.6 s受到扰动后，采用两种控制方法的磁悬浮系统的悬浮气隙均产生偏移和振荡并开始动态回调，滑模控制系统振荡大并且需要0.2 s回调到期望值，而神经网络的模糊滑模控制系统振荡小，只需要0.05 s就可恢复稳定，说明神经网络的模糊滑模控制系统的响应速度快，并且对于不确定性扰动具有鲁棒性.

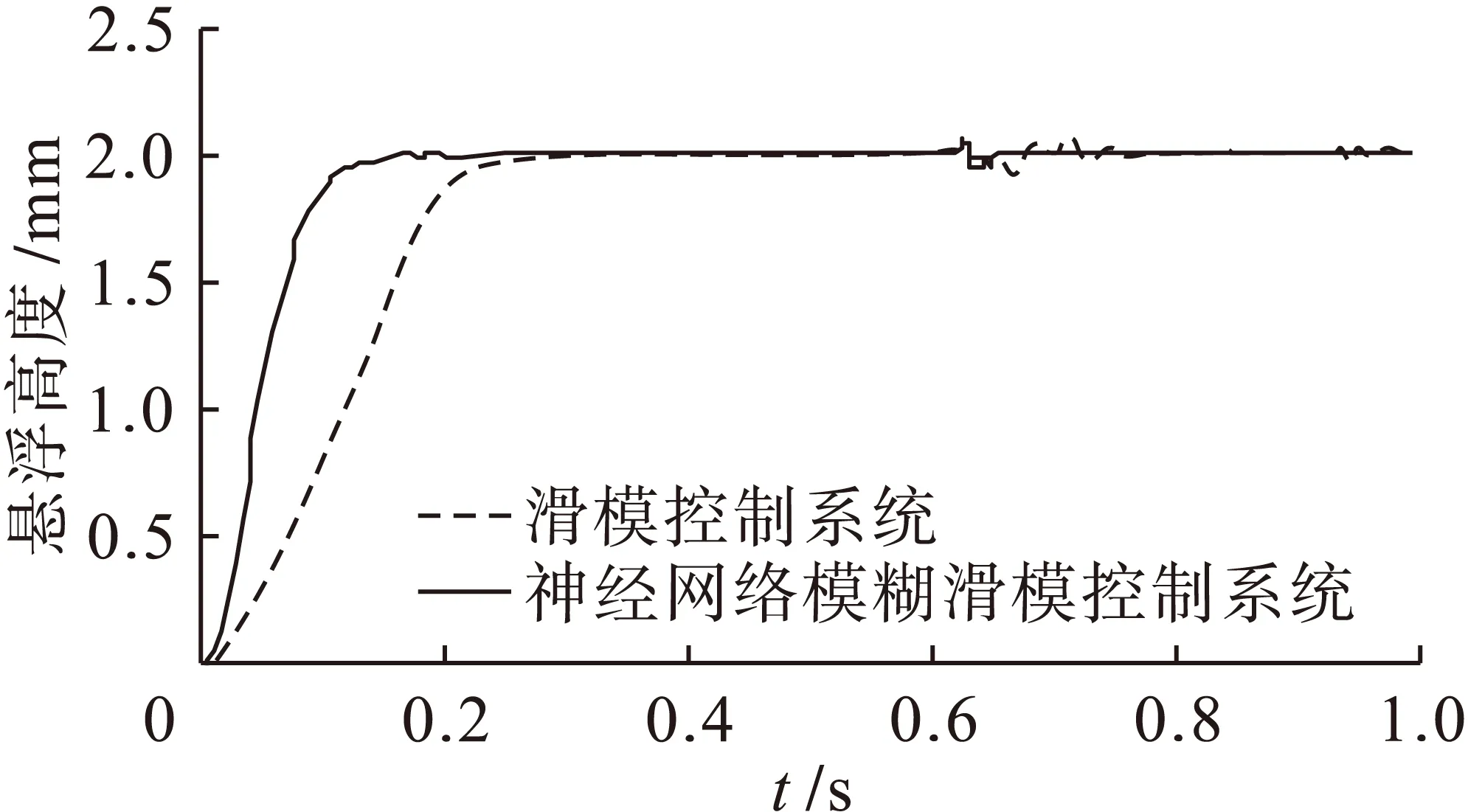
图10　两种控制系统的输出曲线比较

4　结　论

采用基于神经网络的模糊滑模控制方法对单电磁悬浮系统被控对象进行控制.该方法的引入大大加强了控制器的鲁棒性，并且削弱了系统的抖动.同时在建模过程中，由于坐标变换的引入，消除了反馈线性化过程所带来的模型误差，控制精度也得到了提高.仿真结果表明，与传统的滑模控制方案相比较，该控制方法跟踪能力强，跟踪误差小，并且明显地削弱了滑模面抖动对系统的影响，同时具有响应速度快和鲁棒性强的优点.

[1]王晓亮.磁悬浮直线运动平台的结构设计与优化 [D].济南：山东大学，2013.

(WANG Xiao-liang.The structure’s design and optimization of magnetic levitation linear motion platform [D].Jinan：Shandong University，2013.)

[2]张建.数控机床横梁磁悬浮系统的先进滑模控制策略研究 [D].沈阳：沈阳工业大学，2013.

(ZHANG Jian.Study of advanced sliding mode control theory used in magnetic levitation system for NC tool [D].Shenyang：Shenyang University of Techno-logy，2013.)

[3]刘春芳，朱思佳.数控加工中心磁悬浮控制系统混沌预测 [J].沈阳工业大学学报，2014，36(6)：607-612.

(LIU Chun-fang，ZHU Si-jia.Control of electro-magnetic system of CNC machine tools based on T-S fuzzy model reference adaptive [J].Journal of Shen-yang University of Technology，2014，36(6)：607-612.)

[4]Al-Muthairi N F，Zribi M.Sliding mode control of a magnetic levitation system [J].Mathematical Problems in Engineering，2004，2：93-107.

[5]刘春芳，迟青光，郭庆鼎.机床横梁磁悬浮系统的动态积分滑模变结构控制器的设计 [J].制造技术与机床，2011(2)：73-76.

(LIU Chun-fang，CHI Qing-guang，GUO Qing-ding.To design a dynamic integral sliding mode control for the NC tool crossbeam magnetic levitation system [J].Manufacturing Technology & Machine Tool，2011(2)：73-76.)

[6]Phuah J S，Lu J M，Yahagi T.Chattering free sliding mode control in magnetic levitation system [J].IEEE Transactions on Electronics，Information and Systems，2005，125(4)：600-606.

[7]刘春芳，安明伟，王丽梅.移动式数控机床横梁磁悬浮系统的滑模-H∞控制 [J].沈阳工业大学学报，2010，32(4)：443-448.

(LIU Chun-fang，AN Ming-wei，WANG Li-mei.Sli-ding mode-H∞control of crossb earn magnetic levitation system in moving numerical control machining tool [J].Journal of Shenyang University of Techno-logy，2010，32(4)：443-448.)

[8]王通，迟青光.机床横梁悬浮系统的反演自适应动态积分滑模变结构控制研究 [J].机床与液压，2011，39(9)：16-18.

(WANG Tong，CHI Qing-guang.Study on machine tool crossbeam magnetic levitation system based on backstepping self-adaptive dynamic sliding mode control [J].Machine Tool & Hydraulics，2011，39(9)：16-18.)

[9]裴硕，肖平，翟春燕，等.基于模糊神经网络的滑模控制算法 [J].科学技术与工程，2010，10(4)：900-903.

(PEI Shuo，XIAO Ping，ZHAI Chun-yan，et al.Algorithm of sliding mode control based on fuzzy neural network [J].Science Technology and Engineering，2010，10(4)：900-903.)

[10]孙博.基于模糊神经网络的磁悬浮导向系统滑模控制 [D].沈阳：沈阳工业大学，2013.

(SUN Bo.Sliding mode control based on fuzzy neural network on maglev guiding system [D].Shenyang：Shenyang University of Technology，2013.)

[11]胡庆，孙博，于海燕，等.直线电梯单电磁导向装置悬浮气隙高度控制 [J].沈阳工业大学学报，2013，35(3)：251-256.

(HU Qing，SUN Bo，YU Hai-yan，et al.Maglev airgap altitude control of single electromagnetic guiding actuator for linear elevator [J].Journal of Shenyang University of Technology，2013，35(3)：251-256.)

(责任编辑：钟媛英文审校：尹淑英)

Neural network fuzzy sliding mode control for single electromagnetic levitation system

LIU Chun-fang, HU Yu-wei

(School of Electrical Engineering, Shenyang University of Technology, Shenyang 110870, China)

In order to actualize the precise control of levitation airgap in the single eletromagnetic levitation system, a fuzzy sliding mode control scheme based on neural network was proposed. According to the dynamic nonlinear mathematical model for the single eletromagnetic levitation system, the sliding surface which could make the system state reach the stable point within the finite time was designed. Simultaneously, according to the switching state of sliding mode, the gain of control amount in sliding mode was evaluated through introducing the fuzzy control method of neural network. In addition, the control amount of sliding mode was adjusted in real time, and the softening of switching control signal was actualized. The fuzzy sliding mode control system based on the neural network can not only track the given signal, but also weaken the chattering of sliding-mode control and posses global robustness to the external disturbance. The simulated results show that the designed control system has zero overshoot, fast tracking performance and strong robustness to external variation.

magnetic levitation technology; single electromagnetic leviation system; sliding mode control; fuzzy inference; robustness; zero overshoot; neural network; nonlinear control

2015-07-14.

国家自然科学基金资助项目(50805098).

刘春芳(1975-)，女，黑龙江齐齐哈尔人，教授，博士，主要从事伺服系统、鲁棒控制及计算机仿真等方面的研究.

10.7688/j.issn.1000-1646.2016.01.01

TP 273

A

1000-1646(2016)01-0001-06

*本文已于2015-10-16 11∶23在中国知网优先数字出版. 网络出版地址： http：∥www.cnki.net/kcms/detail/21.1189.T.20151016.1123.002.html

电气工程