非线性半参数统计模型估计函数的几何方法
2016-09-13周路平冯予
周路平,冯予
(南京理工大学理学院,江苏 南京 210094)
非线性半参数统计模型估计函数的几何方法
周路平,冯予
(南京理工大学理学院,江苏 南京210094)
将非线性半参数统计模型的概率密度函数族视为统计流形,利用微分几何方法,建立非线性半参数统计模型相对应的Hilbert空间,进而研究非线性半参数统计模型的估计函数问题.利用两类得分函数张成的子空间对Hilbert空间进行正交分解,进而讨论估计函数所在的集合,以及如何选取最优估计函数的问题.最后,通过实例分析来验证此方法的有效性.
估计函数;得分函数;有兴趣参数;冗余参数
1 引言
近年来,半参数统计模型受到了许多统计学者的关注[1],这是因为半参数统计模型不仅具有非参数统计模型的变通性,同时保持了参数统计模型的可解释性.1986年,文献[2]在分析电力需求与气候变化之间的关系时提出了部分线性模型,其形式为:

注意到模型(1)中,第一部分是θ和x的线性关系,而在实际应用中,严格的线性关系并不多见,它们大多带有某种程度的线性近似.随着近代统计学的发展,非线性统计模型在理论研究和实践中的作用日趋重要.因此,引入非线性半参数统计模型[3]:

其中,θ视为m维有兴趣参数,f为已知的非线性函数,k(.)为未知的冗余光滑函数,(x,y,t)是
来自总体(X,Y,T)的独立同分布样本.假设ε服从标准正态分布,则有
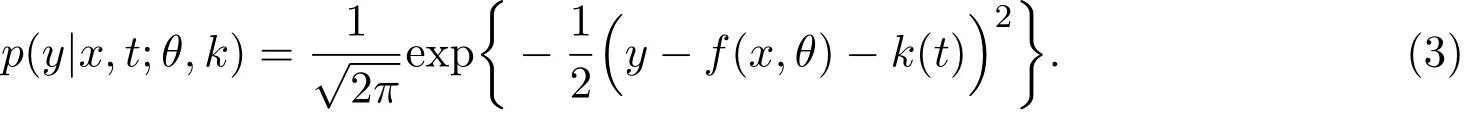
由于统计模型的概率分布族由参数集来描述,而分布族的性质就使得参数空间有着几何性质和几何结构,因此可以用几何方法解决统计学中的问题[48],本文从以下几个问题出发,利用微分几何方法解决非线性半参数统计模型(2)的估计函数问题.第一,估计函数所在集合的几何结构;第二,什么条件下存在估计函数;第三,估计函数相应估计量的渐近性质.
2 估计函数的定义
设y(x,θ)=(yi(x,θ),i=1,...,m)是有兴趣参数θ的向量值光滑函数,维数与θ的维数相同.如果y(x,θ)满足以下三个正则条件:
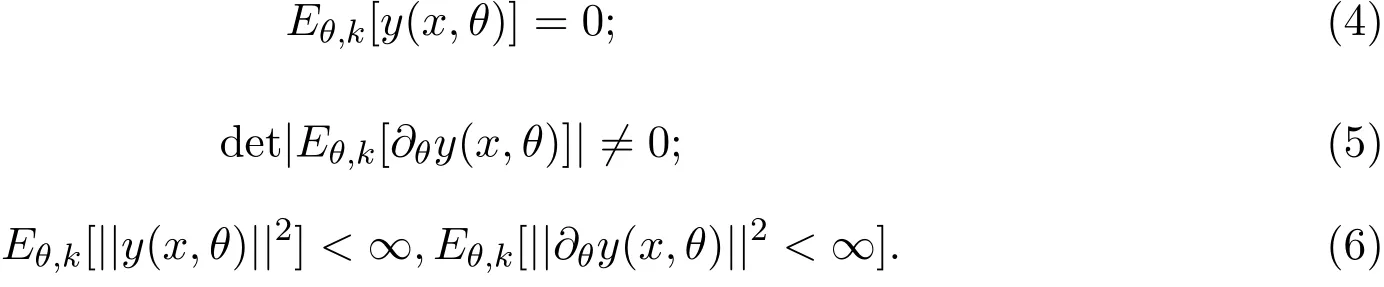
则称y(x,θ)为估计函数.其中Eθ,k表示非线性半参数统计模型的密度函数p(y|x,t;θ,k)对应的期望,∂θy(x,θ)表示y(x,θ)关于θ的偏导数,且det|.|表示矩阵的行列式,||y||2表示向量y范数的平方,即||y||2=Σ(yi)2.
3 非线性半参数统计模型估计函数所在集合的结构
给定非线性半参数统计模型S={p(y|x,t;θ,k)},其相应的Hilbert空间与参数集中的点(θ,k)有关,记为Hθ,k.为了研究估计函数所在集合的几何结构,首先定义非线性半参数统计模型的两类得分函数,由得分函数张成相应的子空间,再对Hθ,k进行正交分解.
3.1沿着有兴趣参数方向的得分函数
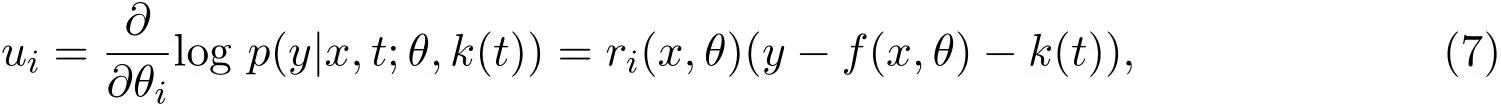
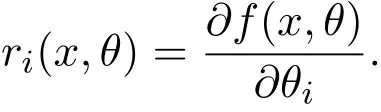
称为非线性半参数统计模型沿着有兴趣参数θ第i个分量θi的得分函数,其中易见Eθ,k[ui]=0,进一步假定ui是平方可积的,则ui∈Hθ,k.将ui沿着有兴趣参数θ方向张成的切空间记为T,非线性半参数统计模型沿着有兴趣参数θ方向的得分函数定义为u=(u1,...,um).
3.2沿着冗余参数方向的得分函数
非线性半参数统计模型沿着冗余参数方向的得分函数定义为:
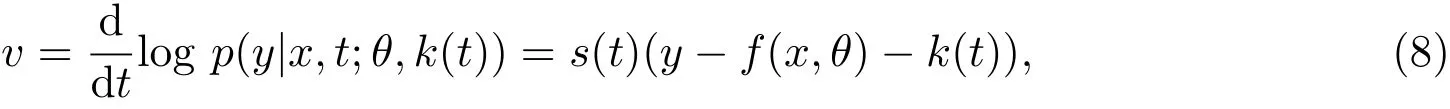
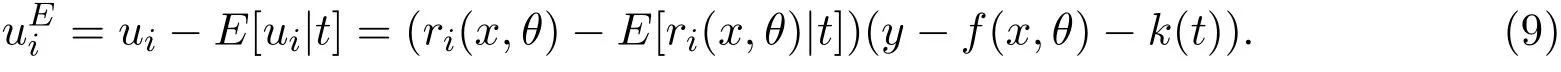
向量uE=(u)称为非线性半参数统计模型的有效得分函数.将有效得分函数的分量uEi张成的子空间记为T,称T⊕T在Hθ,k中的正交补空间为从属切空间,记为T.
下面引入两类转换,即e转换和m转换,进一步分析Hilbert空间Hθ,k的正交分解.
3.3两类转换的定义
假设a(x)是Hilbert空间Hθ,k中一个随机变量,固定θ,考虑集合
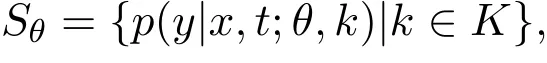
将
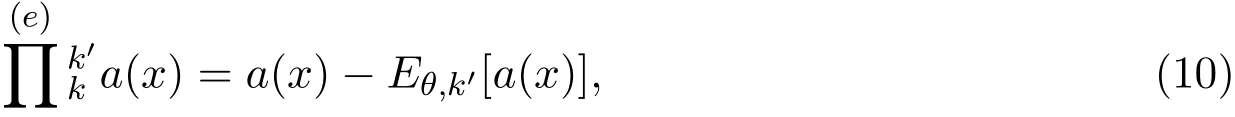
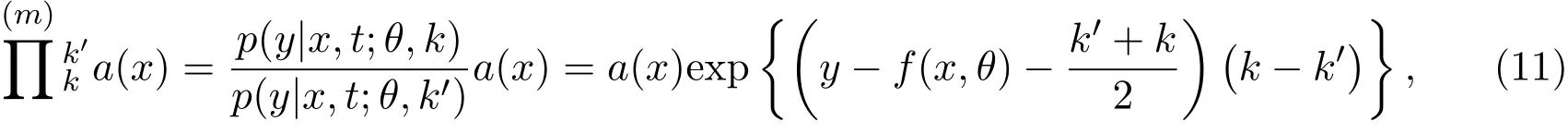
分别定义为a(x)从(θ,k)到(θ,k′)的e转换和m转换.由于
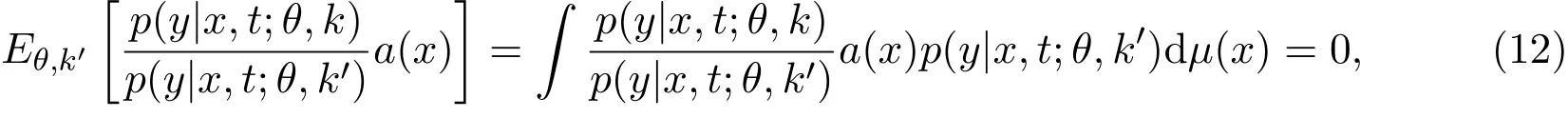
因此

3.3.1e平行转换存在的充要条件
当且仅当a(x)在(θ,k′)处期望存在,a(x)的e平行转换存在,且有

3.3.2两类转换包含于 Hilbert空间的条件
a(x)的e转换和m转换属于Hilbert空间Hθ,k′的充要条件是这两类转换在(θ,k′)处关于p(y|x,t;θ,k′)是平方可积的.
3.4Hilbert空间的正交分解

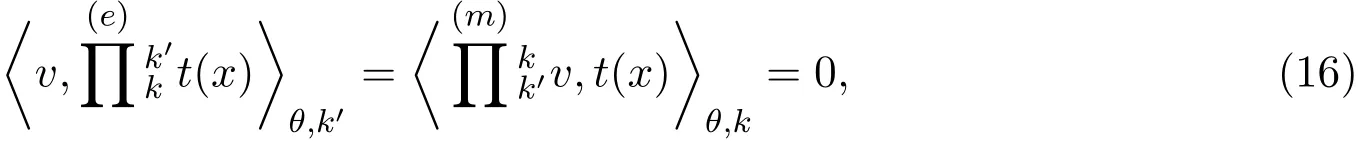
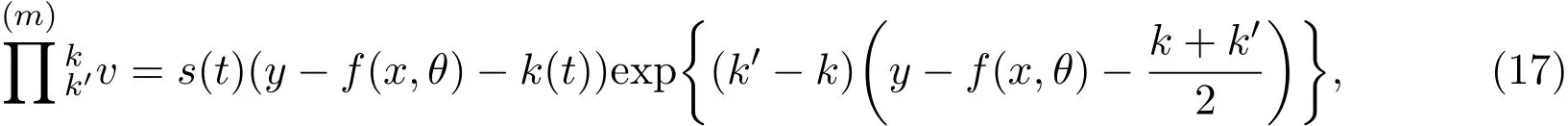
其中将Hilbert空间中满足条件(15)式和(16)式的所有向量构成的闭子空间记为F,其中I表示信息部分,A表示从属部分,显然,有以下关系成立:




通过以上讨论,得到Hilbert空间Hθ,k的一个正交分解

3.5非线性半参数统计模型的估计函数所在集合

定义g(0)=0,对g(t)求导得
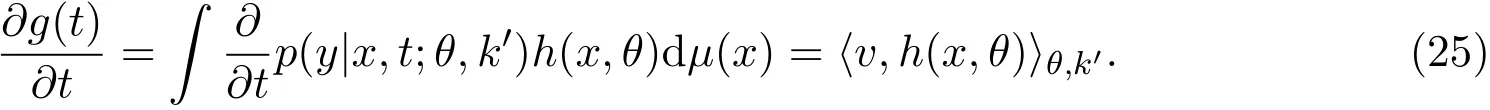
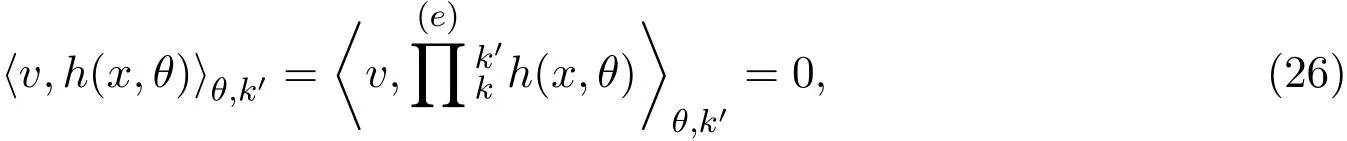
其中

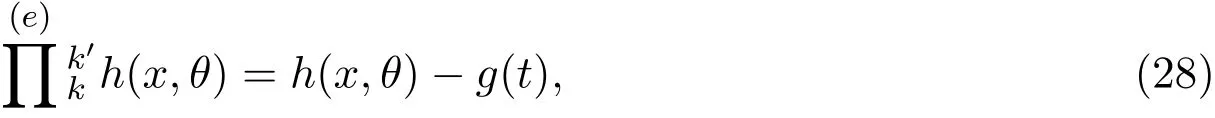

且∀k′∈K,有Eθ,k′[h(x,θ)]=0.若h(x,θ)的分量hi(x,θ)在信息子空间F上的投影向量张成F,并且F是非退化的,则h(x,θ)是非线性半参数统计模型的一个估计函数.
假设y(x,θ)是非线性半参数统计模型(2)的一个估计函数,由正则条件(6)知,在Hilbert空间Hθ,k中y(x,θ)的e转换是存在的,且

易证,对冗余参数k和k′,有

因此

对(4)式关于θ求导数,可得
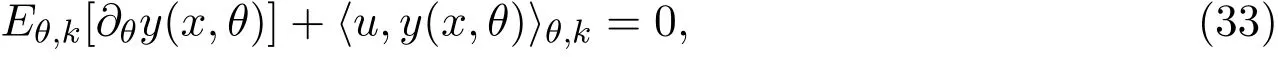
于是有
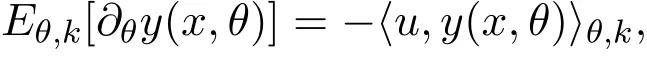
其中u为沿着有兴趣参数θ方向的得分函数,易见u在子空间F⊕F上的投影不包含F的部分,从而由(32)式知,
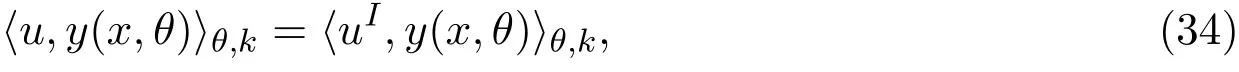
其中uI表示u在F上的投影,易见,对于非线性半参数统计模型(2),有
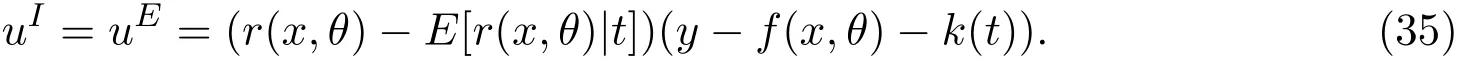
4 估计函数存在条件
由以上讨论知,对于非线性半参数统计模型(2),其估计函数存在的必要条件是信息子空间F非退化,充分条件是固定k0,∀k′∈K,,(i=1,...,m)在F上的投影张成F则uI是一个估计函数,且非线性半参数统计模型的任意估计函数y(x,θ)均可以表示为
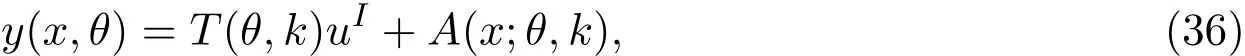
其中 A(x;θ,k)的分量 Ai(x;θ,k)∈T,T(θ,k)是非奇异矩阵.反之,在某个定值 k0处,由(36)式定义的函数y(x,θ)是非线性半参数统计模型的估计函数.取T(θ,k)为单位矩阵,得到一个估计函数

5 估计函数相应估计量的渐近性质以及最优估计函数的选取
5.1估计量的渐近性质
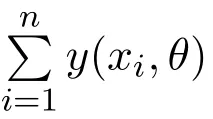

将(38)式在θ处展开,得
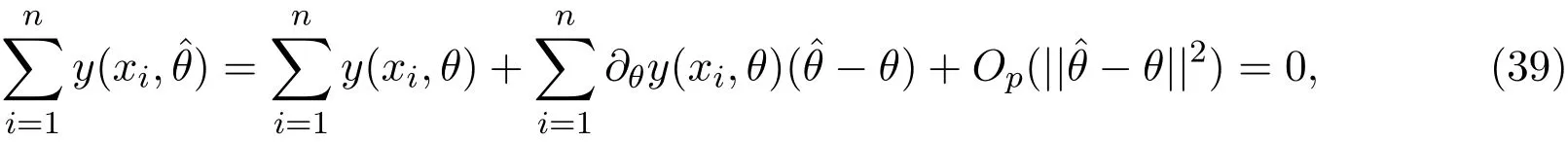

z是服从正态分布N(0,C)的随机变量,

从而忽略高阶项,可得(ˆθ-θ)依分布收敛于B-1z,因此
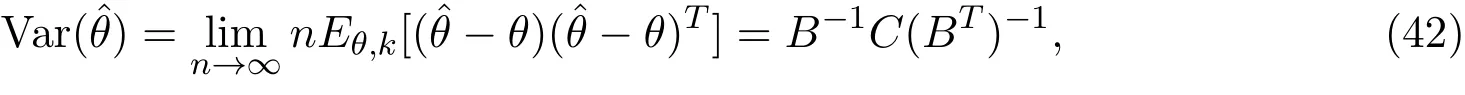
换言之,由(38)式得到的估计量 ˆθ服从渐近正态分布,其渐近协方差即为(42)式.由此可知,(37)式定义的估计函数相应的估计量 ˆθ具有协方差阵

其中
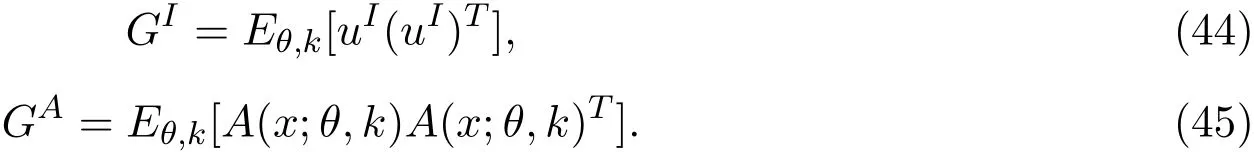
5.2最优估计函数
5.2.1最优估计函数的定义
设估计函数y(x,θ)相应的估计量为ˆθ,如果对于任意估计量 ˆθ′,有

则称y(x,θ)为最优估计函数.其中Var(θ)表示θ的方差.
5.2.2最优估计函数的选取
当非线性半参数统计模型的真分布恰好由(θ,k0)定义,其中k0∈K是固定的,并且对于∀k∈K,张成F,则
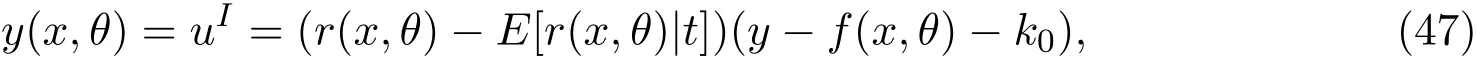
是一个估计函数,且(47)式相应的估计量 ˆθ的渐近协方差阵为Var(ˆθ)=(GI)-1,易见,对于θ任意估计量 ˆθ′,均有Var(ˆθ)≤Var(ˆθ′),因此,由(39)式定义的估计函数为非线性半参数模型的最优估计函数.
6 实例分析
对于非线性半参数统计模型(2),利用权函数估计方法取最优估计函数(39)式中的k0(t) 为k(t)的权函数估计,即
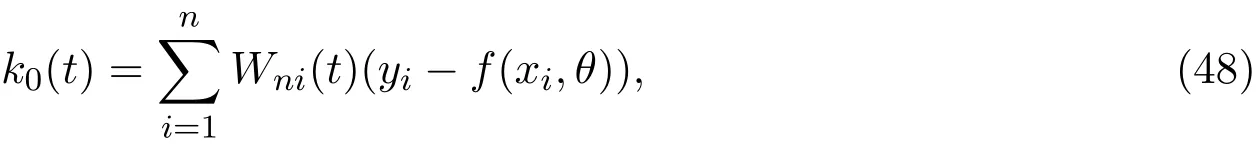
其中
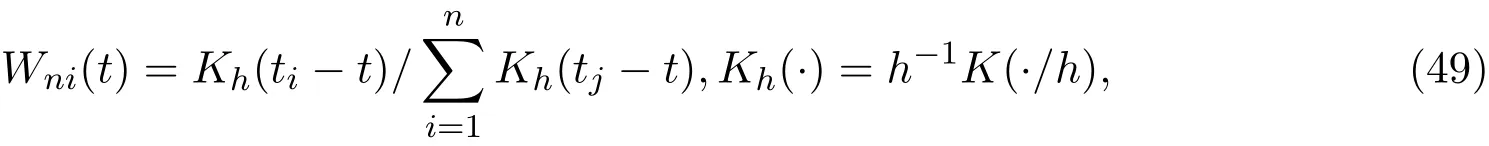
假设x,t服从[0,1]上的均匀分布,则最优带宽h=0.274,其中K(.)取高斯核,即

下面分别考虑θ是一维和二维两种简单情形,来验证微分几何方法的有效性. 例6.1取

则

从而知非线性半参数统计模型

的最优估计函数为
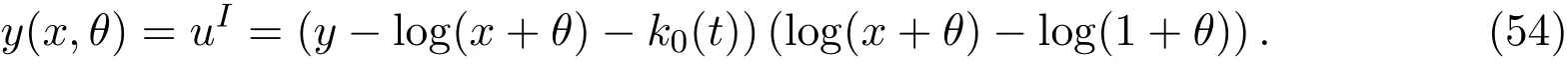
由

得到θ的一个估计量ˆθ=-0.0161,且ˆθ对应的渐近方差为Var(ˆθ)=0.7433,残差平方和
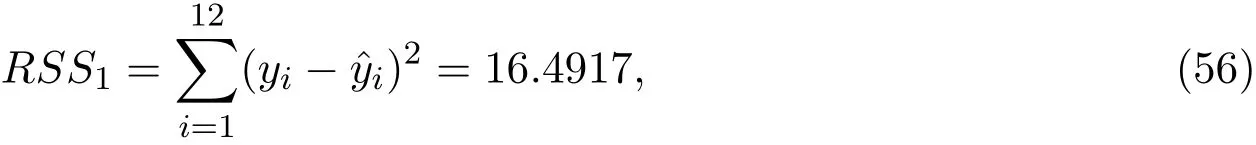
其中

取
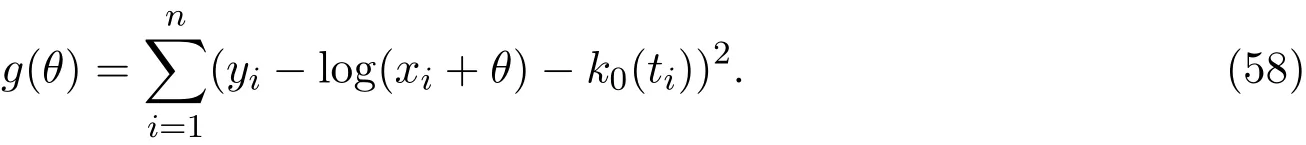
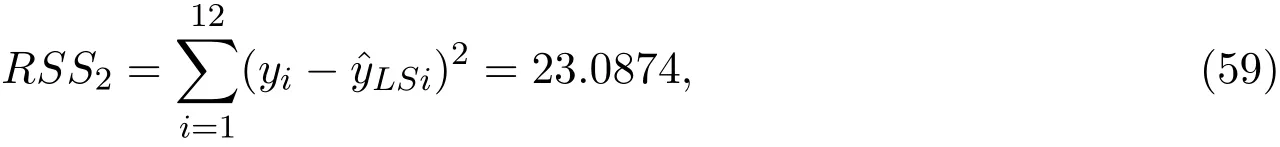
其中
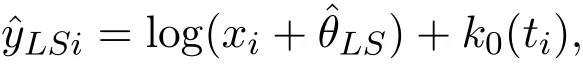
易见
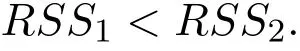
其数据见表1.
例6.2取

则
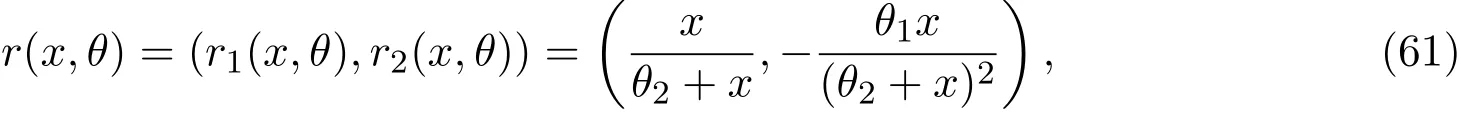
从而知,最优估计函数的两个分量分别为:
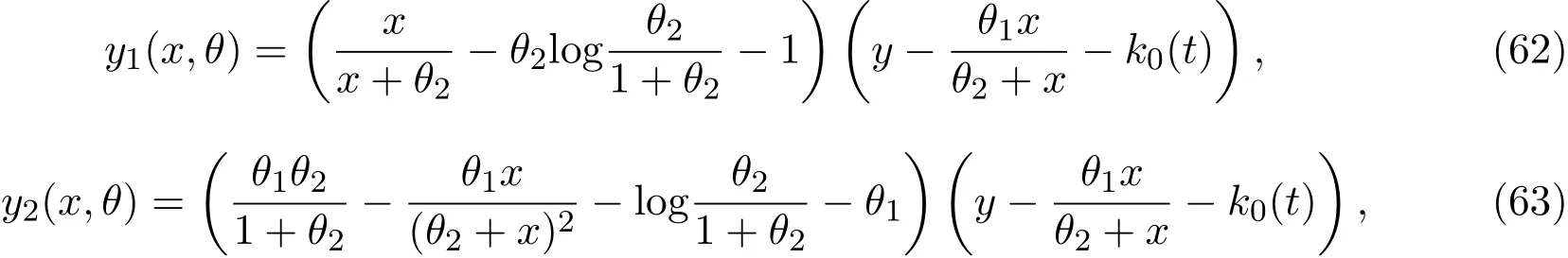
因此,非线性半参数统计模型

的最优估计函数为

由

j=1,2,得到θ的估计量
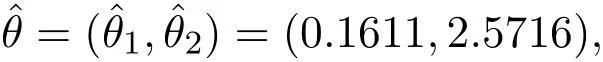
对应的残差平方和
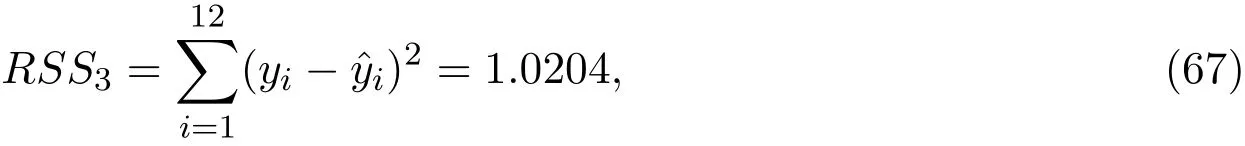
其中

令
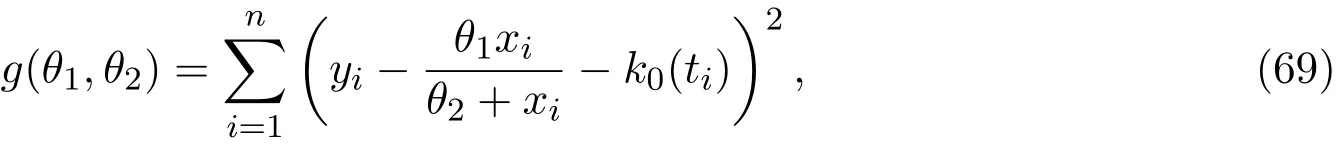
由
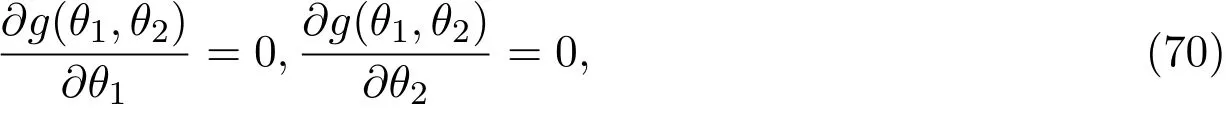
得到θ的最小二乘估计量为
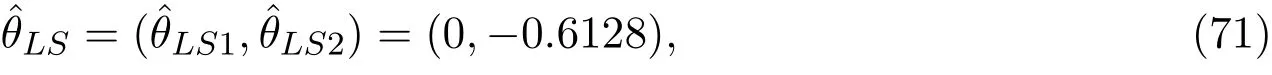
对应的残差平方和
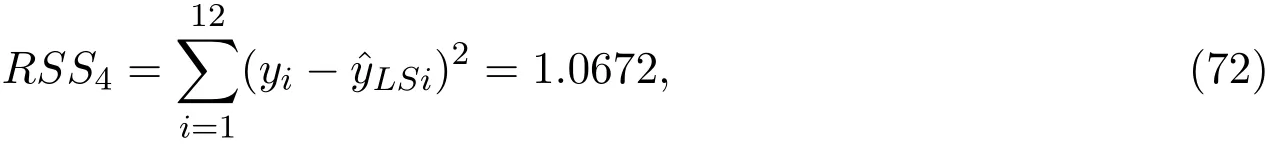
其中

易见
其数据见表2.
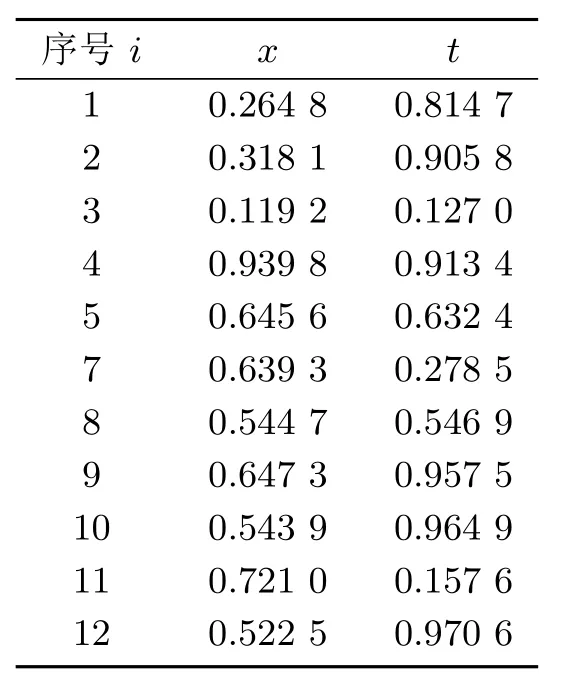
表2 例题6.2数据
2 结束语
非线性半参数统计模型作为半参数模型的一种推广,它综合了非线性回归和非参数回归模型,吸收了各自的优点.利用微分几何方法对非线性半参数统计模型进行分析,解决了以下几个主要问题,即估计函数所在集合,估计函数存在条件,估计函数相应估计量的渐近性质以及如何选取最优估计函数.在文章最后的两个例子中,用微分几何方法进行参数估计优于最小二乘方法.微分几何方法进行参数估计是否在所有统计模型的参数估计问题中都比最小二乘方法有效?这一问题还有待进一步探讨.
[1]Xue L G,Xue D.Empirical likelood for semiparametric regression model with missing response data[J]. Journal of Multivariate Analysis,2011,102(4):723-740.
[2]Engle.Semiparametric estimates of the relation between weather and electricity sales[J].Journal of the American Statistical Association,1986,81(394):310-320.
[3]Wierzbicki M R,Guo L B,Du Q T,Guo W.Sparse semiparametric nonlinear model with application to chromatographic fingerprints[J].Journal of the American Statistical Association,2013,109(508):1339-1349. [4]Amari S.Differential Geometrical Methods in Statistics(Lecture Notes in Statistics)[M].Berlin:Springer-Verlag,1990.
[5]Amari S.Dual connections on the Hilbert bundles of statistical models[J].Geometrization of Statistical Theory,1987,3(1):123-152.
[6]Amari S.Estimation in the presence of infinitely many nuisance parameters-Geometry of estimating function [J].The Annals of Statistics,1988,16(3):1044-1068.
[7]Amari S,Han T S.Statistical inference under multiterminal rate restrictions[J].IEEE Information Theory,1989,35:217-227.
[8]Amari S.Information geometry of estimating functions in semi-parametric statistical models[J].Bernoulli,1997,3(1):29-54.
[9]Fu Y Z,Chen X D.Model selection of generalized partially linear models with missing covariates[J].Journal of Statistical Planning and Inference,2012,142(1):126-138.
[10]Liu W,Wu L.Some asymptotic results for semiparametric nonlinear mixed-effects models with incomplete data[J].Journal of Statistical Planning Inference,2010,140(1):52-64.
2010 MSC:62G86
Geometry method of estimating functions in nonlinear semiparametric models
Zhou Luping,Feng Yu
(School of Science,Nanjing University of Science and Technology,Nanjing210094,China)
The probability density function family of nonlinear semi-parametric statistical model are considered as a statistical manifold.Using the methods of differential geometry to construct Hilbert space corresponding to nonlinear semiparametric model,and then study some questions of estimation function.Using the subspace spanned by two kinds of score function to decompose the Hilbert space orthogonally,and then discuss the set of the estimated function is located,and how to select the best estimate of function problems.Finally,through the analysis of examples to verify the effectiveness of this method.
estimating function,score function,interesting parameter,nuisance parameter
O212
A
1008-5513(2016)04-0351-11
10.3969/j.issn.1008-5513.2016.04.004
2016-01-17.
国家自然科学基金(11271189).
周路平(1988-),硕士生,研究方向:统计推断与微分几何.
