非负矩阵Perron根的下界序列

钟琴，周鑫，牟谷芳

（1.四川大学锦江学院数学教学部，四川 彭山　620860；2.乐山师范学院数学与信息科学学院，四川 乐山　614000）

非负矩阵Perron根的下界序列

钟琴1，周鑫1，牟谷芳2

（1.四川大学锦江学院数学教学部，四川 彭山620860；2.乐山师范学院数学与信息科学学院，四川 乐山614000）

非负矩阵Perron根的估计是非负矩阵理论研究的重要课题之一.如果其上下界能够表示为非负矩阵元素的易于计算的函数，那么这种估计价值更高.本文结合非负矩阵的迹分两种情况给出Perron根的下界序列，并且给出数值例子加以说明.关键词：非负矩阵；Perron根；下界序列

1　引言和记号

非负矩阵Perron根的理论在很多领域有重要应用.在实际中，常常需要估计非负矩阵的最大特征值.对于非负矩阵最大特征值下界的估计，也得到了广泛的研究.

首先，为了方便和叙述，本文采用以下的符号和记法.

不失一般性，假设n阶矩阵A≥0，ρ(A)表示非负矩阵A的谱半径，对i=1，2，...，n，ri(A)表示矩阵A的第i行行和，R(A)和r(A)分别表示矩阵A的最大行和与最小行和，C(A) 和c(A)分别表示矩阵A的最大列和与最小列和.

以下是众所周知的Frobenius定理[1]：

正矩阵是非负矩阵的子类，具有非负矩阵的所有性质.文献［2-4］在(1)式的基础上给出了正矩阵最大特征值的界值定理.

定理 1.1[2]设A=(aij)n×n＞0且r＜R，则其最大特征值ρ(A)满足：

其中

定理 1.2[3]设A=(aij)n×n＞0，则其最大特征值ρ(A)满足：

其中r，R，η的定义同定理1.

定理 1.3[4]设A=(aij)n×n＞0，则其最大特征值ρ(A)满足：

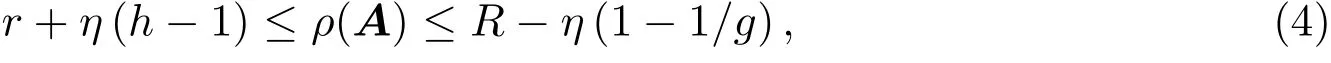
其中r，R，η的定义同定理2，

关于正矩阵最大特征值的界，在涉及r，R和η的一切可能的界值中，Brauer的结果是最好的.

本文结合非负矩阵的迹分两种情况给出Perron根的下界序列，从而有效的改进Perron根的下界，并且给出数值例子加以比较.

2　Perron根的下界估计

首先简要介绍一下相关的定理.

引理 2.1[5]若x1，x2，...，xn均为实数且满足xn≤xn-1≤...≤x1，则有

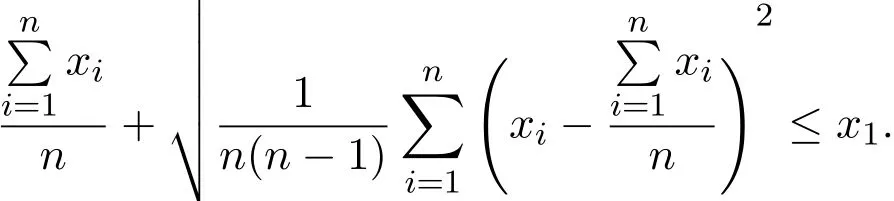
推论 2.1若y1，y2，...，yn均为实数，k为任意的正整数，则有

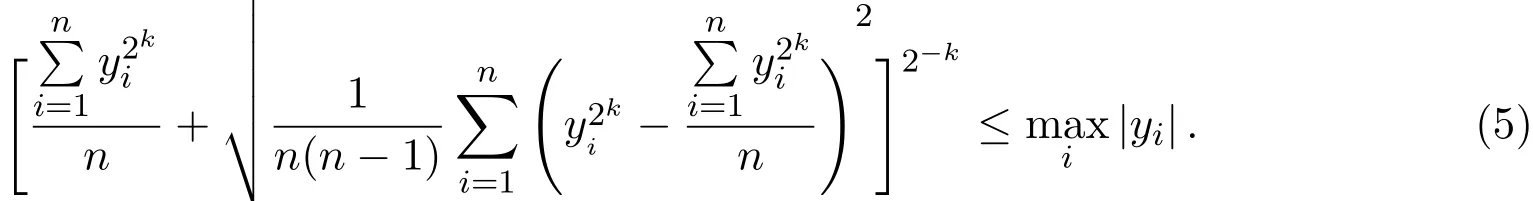
此式即(5)式.

引理 2.2[6]若y1，y2，...，yn均为实数，令

k为任意的正整数，则序列

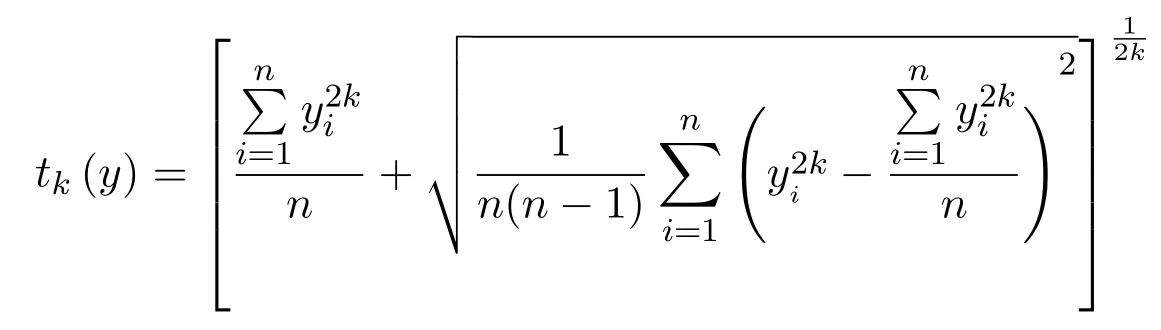
为单调递增序列.

在引理2.2的基础上，显然序列

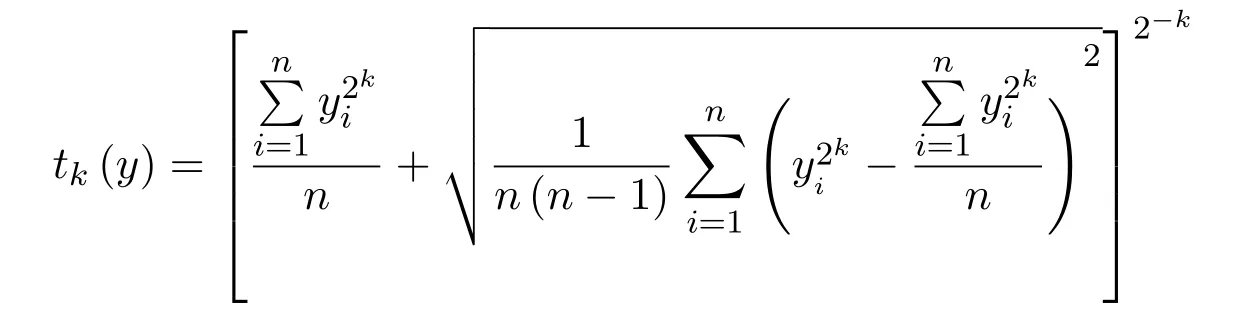
也为单调递增序列.

本文在上述结果的基础上，分两种情况给出非负矩阵Perron根的下界序列.

定理2.1设A≥0，且AT=A.则序列

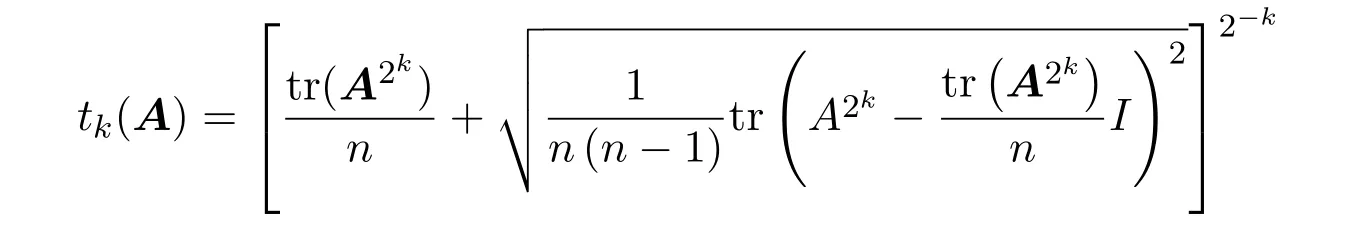
为单调递增序列，且tk(A)≤ρ(A).

证明由A≥0，且AT=A，可知A的特征值λ1，λ2，...，λn均为实数，且

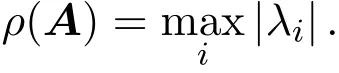
令λ=(λ1，λ2，...，λn)，根据上面的讨论可知序列

为单调递增序列，且tk(λ)≤ρ(A).注意到

即得序列

为单调递增序列，且

以上讨论的是当A为非负对称矩阵时的情况，当A≥0但A不对称时，构造矩阵A的几何对称矩阵

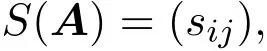
其中

显然矩阵S(A)满足定理2.1的条件，此时有：

定理2.2设A≥0，令S(A)=(sij)，其中

则序列

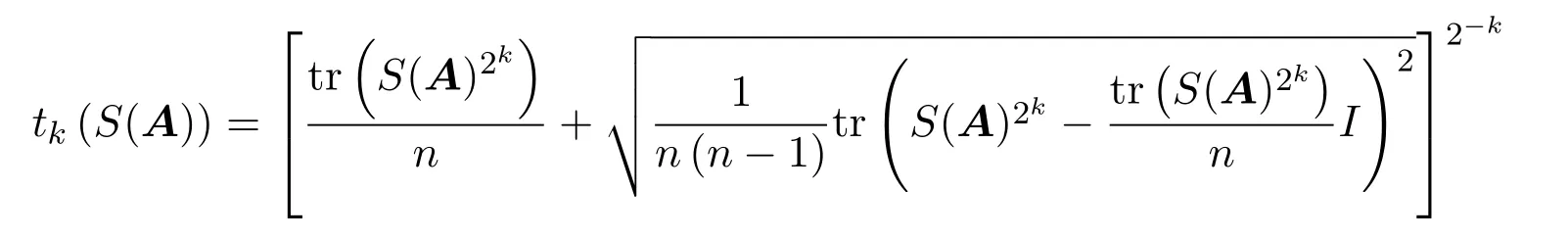
为单调递增序列，且

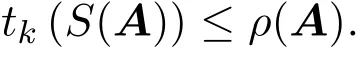
证明将定理2.1应用到矩阵S(A)并注意到ρ(S(A))≤ρ(A)即得.

注2.1当A为非负对称矩阵时，S(A)=A，定理2.1实际上是定理2.2的特殊情形.

3　数值例子

例3.1考虑非负对称矩阵

对于非负对称矩阵A的Perron根的下界，运用定理2.1有下面的比较结果(见表1).实际上ρ(A)≈9.4669，从数据来看，估计结果是很精确的.

对于非负矩阵B的Perron根的下界，运用定理2.2有下面的比较结果(见表2).

例3.2考虑非负矩阵

实际上ρ(B)≈5.7417，从数据来看，估计结果是很精确的.

表1　非负对称矩阵A的Perron根的下界比较结果

表2　非负矩阵B的Perron根的下界比较结果

从以上的两个例子可以看出，对一个非负矩阵，不管其对称还是非对称，都可以构造一个基于矩阵迹的单调递增序列，从而有效的改进Perron根的下界.

[1］Berman A，Plemmons R J.Nonnegative Matrices in Mathematical Sciences[M］.Philadelphia：SIAM Press，PA，1994.

[2］Ledermannn W.Bounds for the greatest latent root of a positive matrix[J］.London Math.Soc.，1950，25：265-268.

[3］Ostrowski A.Bounds for the greatest latent root of a positive matrix[J］.London Math.Soc.，1952，27：253-256.

[4］Brauer A.The theorem of Ledermann and Ostrowski on positive matrices[J］.Duke Math.，1957，24：265-274.

[5］Wolkowicz H，Styan G P H.Bounds for eigenvalues using traces[J］.Linear Algebra Appl.，1980，29：471-506.

[6］Rojo O，Soto R，Rojo H.Bounds for the spectral radius and the largest singular value[J］.Computers Math. Applic.，1998，36（1）：41-50.

2010 MSC:15A48

A sequence of lower bounds for the Perron root of a nonnegative matrix

Zhong Qin1，Zhou Xin1，Mou Gufang2
（1.Department of Mathematics，Sichuan University Jinjiang College，Pengshan620860，China；2.College of Mathematics and Information Science，Leshan Normal University，Leshan614000，China）

Computing the bounds for the greatest characteristic root of a nonnegative matrix is important part in the theory of nonnegative matrices.It is more practical value when their bounds are expressed easily calculated function in element of matrix.In this paper，we obtain an increasing sequence of lower bounds for the Perron root of a nonnegative matrix based on the trace of matrix.Numerical examples are given to illustrate the method is effective.

nonnegative matrices，Perron root，lower bound

O151.21

A

1008-5513(2016)04-0331-06

10.3969/j.issn.1008-5513.2016.04.001

2016-04-18.

四川省教育厅科研项目(13ZB0357)；四川大学锦江学院青年教师科研基金(12130219).

钟琴(1982-)，硕士，副教授，研究方向：矩阵的特征值估计和数值计算.