基于分数阶偏微分方程和CB模型的彩色图像去噪方法

周　千

(西安航空学院理学院　西安　710077)



基于分数阶偏微分方程和CB模型的彩色图像去噪方法

周千

(西安航空学院理学院西安710077)

将分数阶偏微分理论和CB模型相结合应用于图像去噪,提出了一种基于分数阶偏微分方程和CB模型的彩色图像去噪方法。首先,将一副彩色图像分解为色度C和亮度B两部分,然后用分数阶偏微分模型处理亮度B,而对于色度C,由于其受到单位长度的限制,在处理时非常困难,利用拉格朗日乘数法并通过添加辅助变量,将色度转化为两个近似的子问题,从而得到色度的近似处理方法,最后将处理后的亮度B和色度C合成为新的彩色图像。最后通过实验证明了该方法的有效性。

彩色图像去噪; 分数阶偏微分方程; CB模型

Class NumberTP391

1　引言

图像去噪是图像处理和图像分析领域中的一个重要研究课题。但是,一般的图像去噪模型都是针对灰度图像进行处理[1～5]。然而,在实际生活中,人们接触到的图像主要是彩色图像,因此,对彩色图像进行去噪处理[6～9]具有非常重要的现实意义。传统的彩色图像处理方法都是采用RGB空间,分别对彩色图像的红、绿、蓝三分量进行处理,最后再将处理后的三个分量合成彩色图像。虽然这种方法具有实现过程简单、处理速度快等特点,但由于彩色图像的三个分量原本是一个有机的整体,相互之间具有很高的相关性,将RGB三个分量分开处理往往会导致最终得到的彩色图像失真,降低去噪后彩色图像的质量。

针对传统彩色图像去噪方法出现的阶梯效应以及采用RGB三分量分开处理时所产生的图像失真等缺点,本文提出一种基于分数阶偏微分方程[10]和CB(Chromaticity-Brightness)模型的彩色图像去噪方法。首先,将一幅彩色图像I分为色度C(Chromaticity)和亮度B(Brightness)两部分,其中,

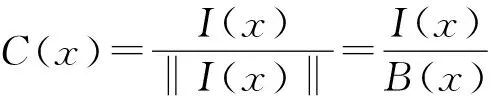
这里,‖·‖表示L2范数。亮度B表示RGB彩色向量的长度,色度C用来存储单位长度上的彩色信息。对于亮度B,大多数的研究者采用TV模型(全变分图像去噪模型)进行处理,但TV模型属于二阶偏微分方程的范畴,去噪结果会出现阶梯效应,本文采用分数阶偏微分方程[10]对亮度B进行处理;对于色度C,由于其受到单位长度的限制,在处理时非常困难,本文利用拉格朗日乘数法并通过添加辅助变量,将色度转化为两个近似的子问题,从而得到色度的近似处理方法[8],然后将处理后的亮度B和色度C合成新的彩色图像。最后通过实验证明了该方法的有效性。

2　分数阶偏微分方程图像去噪模型

分数阶微分是整数阶微分的推广,从不同的角度去考查分数阶微分可以得到不同的定义。常用的定义方法有基于时域空间的Riemann-Liouville(R-L)定义和Grunwald-Letnikov定义,还有基于频域空间的Fourier变换域、小波变换域等定义。本文采用基于频域空间的定义,因为其相对简单并且容易实现。

对于任意的函数f(t)∈L2(R),它的Fourier变换为

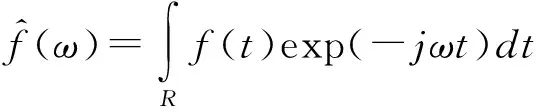
(1)

一阶微分在频域的等价形式为

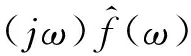
(2)

其中,“↔”表示Fourier变换对。

将整数阶推广到分数阶,可得分数阶微分在频域的等价形式为

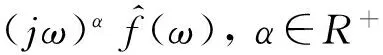
(3)

对于任意给定的二维信号g(x,y)∈L2(R2),其相应的二维Fourier变换为

(4)

因此,其分数阶偏导数形式为

(5)

其中F-1是二维连续Fourier逆变换算子。

基于偏微分方程的图像去噪模型的去噪过程可解释为一个能量泛函的最小化的能量耗散的过程,整数阶偏微分去噪模型的能量泛函为

(6)

式中Ω是图像区域,f(·)≥0是递增函数。

将整数阶推广到分数阶,可得分数阶偏微分去噪模型的能量泛函为

E(u)=∫Ωf(|Dαu|)dΩ

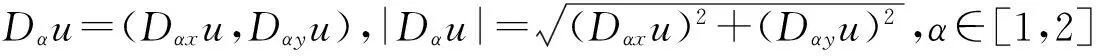
接下来,计算式(7)的欧拉-拉格朗日方程。

取任意的测试函数η∈C∞(Ω)，定义

Φ(a)=∫Ωf(|Dαu+aDαη|)dxdy

(8)

可得:

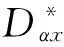
(9)

式(9)可利用如下的最速下降法求解:

(10)

式(10)中,当α=1时,方程就退化为Perona-Malik方程;当α=2时,方程就是四阶各向异性扩散方程。

为了计算的方便,对式(10)中分数阶偏微分的计算如下:

3　基于分数阶偏微分方程和CB模型的彩色图像去噪模型

在RGB空间,一幅彩色图像可以看作一个映射:

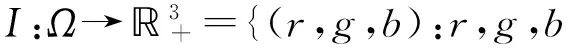
(11)

大多数的图像去噪方法是建立在RGB空间体系上,CB模型也是来源于RGB颜色空间,它把I分为色度C(Chromaticity)和亮度B(Brightness)两部分,其中,

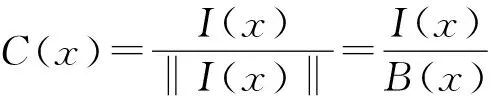
这里,‖·‖表示L2范数。亮度B表示RGB彩色向量的长度,色度C用来存储单位长度上的彩色信息。

对于亮度B,采用基于分数阶偏微分方程的图像去噪模型进行处理,分数阶微分可以大幅提升图像的高频成分、增强图像的中频成分、非线性保留图像的低频成分,因此可以较好地保留图像平滑区域中灰度变化不大的纹理细节信息,同时,还可以避免二阶非线性扩散所特有的“阶梯效应”。

而对于色度C的去噪,首先将C表示为C=(C1,C2,C3),然后考虑:

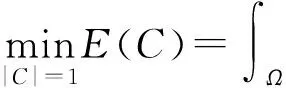
(12)

对式(12),利用拉格朗日乘数法可得到一个无条件极值问题:

(13)

其中μ(x)是在点x∈Ω的拉格朗日乘数。

为了有效地解决问题(13),文献[4]添加了一个新的变量U来近似的代替色度C,并且获得了问题(13)的一个近似问题:

(14)

最后,分别推导出了式中μ,C,U的计算方法:

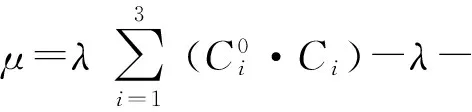
(15)

(16)

(17)

(18)

本文算法实现主要包括以下三个步骤:

1) 把待处理的彩色图像分解为色度C和亮度B两部分;

2) 对于亮度B,将其代入式(10)中进行处理,而对于色度C则利用式(15)～式(18)进行迭代求解;

3) 最后,将处理后的色度C和亮度B合成新的彩色图像。

4　实验结果与分析

为了验证本文模型的有效性,在Matlab7.0的平台下进行了两组比较实验。实验结果主要通过计算去噪后图像的信噪比(SNR)作为去噪性能的客观评价标准。

第一组实验是将本文方法与基于整数阶偏微分方程的图像去噪算法[8]进行比较,实验结果如图1所示。选取标准的Lena图像进行实验,图1(a)是原图,图1(b)是未加噪声的亮度图。由于本文算法中关于色度C的处理是利用文献[8]中的方法,故只给亮度B添加均值为0,方差为0.01的高斯噪声,其中SNR=13.4853,如图1(d)所示,色度C不添加噪声,如图1(c)所示。在文献[8]中,对于亮度B的处理采用Rudin-Osher-Fatemi(ROF)模型[1],而本文算法中对于亮度B的处理则采用分数阶偏微分模型,ROF模型属于二阶偏微分方程去噪模型,有其固有的缺点,即会产生“阶梯效应”,而本文模型去噪后的图像不仅可以抑制大量的噪声,同时又保护了帽檐、头发等边缘文理细节。最后,从实验结果也可以看出,在噪声强度相同的条件下,本文模型处理后得到的图像的SNR=19.1803高于文献[8]中方法处理后得到的图像的SNR=18.5681,从客观角度说明了本文模型的有效性和优越性。

图1　Lena图像及文献[8]方法和本文方法的去噪效果图

第二组实验是将本文方法与传统的基于RGB三通道的图像去噪算法[9]进行比较,实验结果如图2所示。选取标准的Pepper图像进行实验,图2(a)是原图,图2(b)是添加均值为0,方差为0.01的高斯噪声图。图2(c)是基于RGB三通道的图像去噪算法处理的结果,从图中可以看出,该方法处理后的彩色图像有明显的失真现象,特别是在图中红色辣椒的部分,从而降低了去噪后彩色图像的质量,其原因是彩色图像RGB三个分量原本是一个有机的整体,相互之间具有很高的相关性,将RGB三个分量分开处理势必会导致图像失真。图2(d)是本文方法处理的结果,从图中可以看出,本文方法处理后的图像更加接近于原图,视觉效果较好。最后,从实验结果也可以看出,在噪声强度相同的条件下,本文模型处理后得到的图像的SNR=21.1993高于基于RGB三通道的图像去噪算法处理后得到的图像的SNR=16.8106,进而从客观角度说明了本文模型的有效性和优越性。

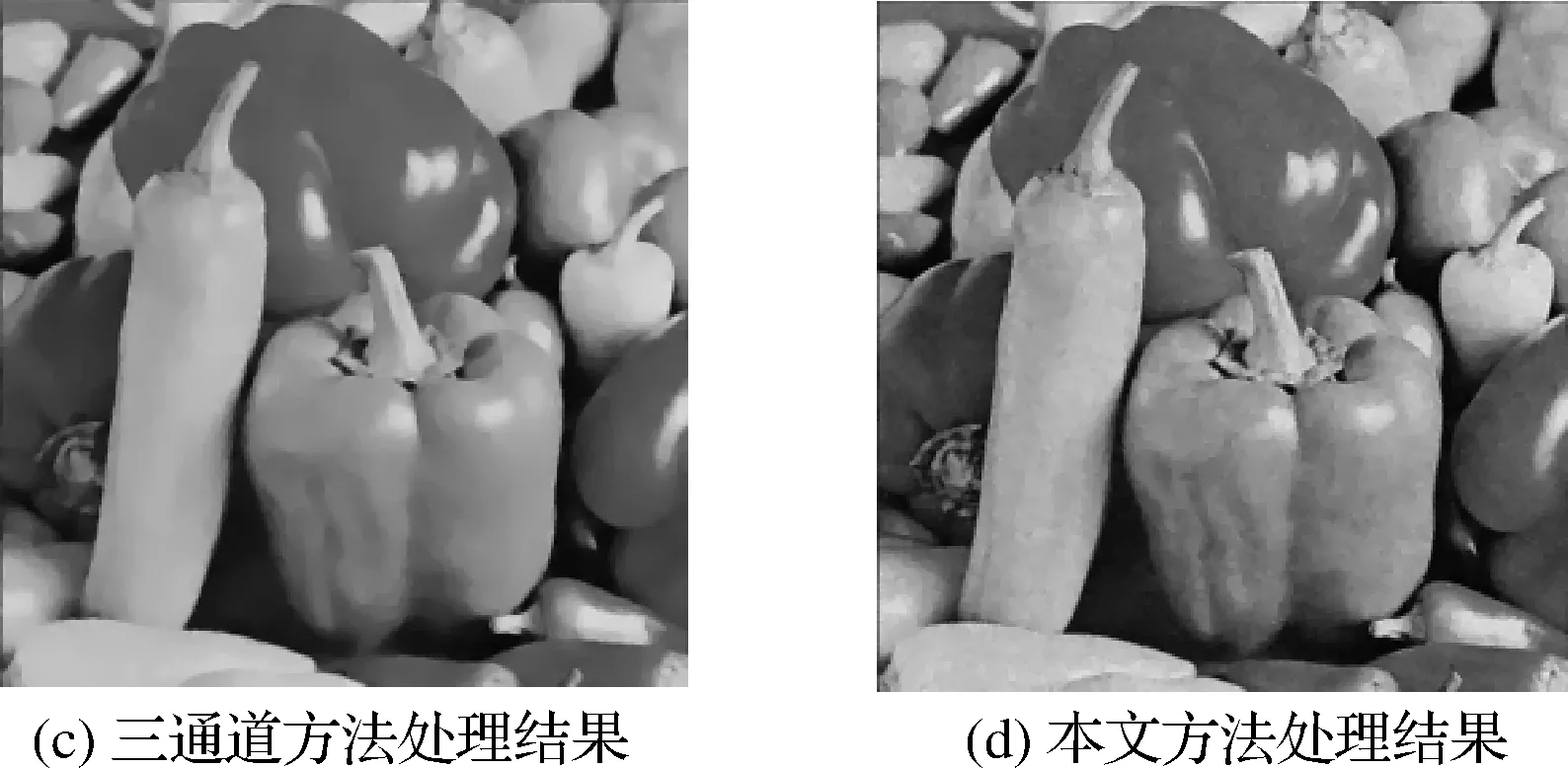
图2　Pepper图像及三通道方法和本文方法的去噪效果图

5　结语

本文将分数阶偏微分理论和CB模型相结合应用于图像去噪,提出了一种基于分数阶偏微分方程和CB模型的彩色图像去噪方法。首先,将一副彩色图像分解为色度C和亮度B两部分,然后用分数阶偏微分模型处理亮度B,利用拉格朗日乘数法并通过添加辅助变量,将色度转化为两个近似的子问题,从而得到色度的近似处理方法,最后将处理后的亮度B和色度C合成为新的彩色图像。实验结果表明,本文提出的方法既能有效的加强图像的纹理信息,并能获得更好地视觉效果。

[1] L. Rudin, S. Osher, E. Faatemi. Nonlinear total variation based noise removal algorithms[J]. Physica D,1992,60(4):259-268.

[2] PERONA P, MALIK J. Scale-space and edge detection using anisot ropic diffusion[J]. Institute of Electrical and Electronics Engineers Transactions on Pattern Analysis and Machine Intelligence,1990,12(7):629-639.

[3] YOU YL, XU W, TANNENBAUM A, et al. Behavioral analysis of anisotropic diffusion in image processing[J]. Institute of Electrical and Electronics Engineers Transactions on Image Processing,1996,5(11):1539-1553.

[4] CATTE F, LIONS PL, MOREL JM, et al. Image selective smoothiung and edge detection by nonlinear diffusion[J]. Society for Industrial and Applied Mathematics Journal of Numerical Analysis,1992,29(1):182-193.

[5] ALVAREZ L, LIONS PL, MOREL JM. Image selective smoothiung and edge detection by nonlinear diffusion[J]. Society for Industrial and Applied Mathematics Journal of Numerical Analysis,1992,29(3):845-866.

[6] T. F. Chan, S. H. Kang, J. Shen. Total variation denoising and enhancement of color images based on the CB and HSV color models[J]. Vis. Commun. Image R,2001,12(4):422-435.

[7] B. Tang, G. Sapiro, V. Caselles. Color image enhancement via chromaticity diffusion[J]. IEEE Trans. Image Process,2001,10(5):701-707.

[8] Fang Li. A novel algorithm for color image denoising based on the CB color model[C]//2011 13thIEEE Joint International Computer Science and Information Technology Conference,2011:67-70.

[9] 杜宏伟,张翼.基于偏微分方程的彩色图像去噪综合模型[J].云南民族大学学报(自然科学版),2011,20(6):497-499.

DU Hongwei, ZHANG Yi. Combined model for color image denoising based on the partial differential equation[J]. Journal of Yunnan University of Nationalities(Nature Sciences Edition),2011,20(6):497-499.

[10] Jian Bai, Xiang-chu Feng. Fractional-Order anisotropic diffusion for image denoising[J]. IEEE Trans. Image Process,2007,16(10):2492-2502.

Novel Color Image Denoising Method Based on Fractional-Order Partial Differential Equation and CB Model

ZHOU Qian

(School of Science, Xi’an Aerotechnical University, Xi’an710077)

Combing fractional-order differential theory with Chromaticity-Brightness(CB) model, a novel image denoising model was proposed, which was based on fractional-order partial differential equation and CB model. Firstly, a color image was decomposed into chromaticity component and brightness component. Secondly, fractional-order differential model was used for brightness component. For chromaticity component, Lagrange multipliers method was used and an auxiliary variable was added to approximate the chromaticity. Thirdly, the retorted image was got by multiplying the recovered chromaticity with recovered brightness. Finally, it proved the validity of the proposed model through the experiment.

color image denoising, fractional-order differential equation, CB color model

2016年2月13日,

2016年3月30日

陕西省教育厅专项科研计划项目(编号:15JK1379);西安航空学院科研基金项目(编号:13XP19；2014KY1210)资助。

周千,男,硕士研究生,讲师,研究方向:基于偏微分方程的图像处理。

TP391

10.3969/j.issn.1672-9722.2016.08.037