基于节点自旋阈值确认机制的无线传感网节点定位算法

张琳娜

(陕西国防工业职业技术学院　西安　710300)



基于节点自旋阈值确认机制的无线传感网节点定位算法

张琳娜

(陕西国防工业职业技术学院西安710300)

为解决无线传感网链路定位过程中定位阈值确定困难,数据链路随定位精度存在迁移过度等问题。论文提出了基于节点自旋阈值确认机制的无线传感网节点定位算法。首先,采取区域自递归方式,构建节点定位自旋阈值,并根据该阈值进行节点定位,从而实现簇区域内节点的稳定搜寻,然后针对数据传输过程的特点,采取流量稳定机制实现对数据传输的优化选择,从而实现数据的高效汇聚传输。仿真实验表明:与SWF算法相比,论文算法的链路稳定代价更低,可实现数据的优化传输和节点的精确定位。

无线传感器网络; 节点定位; 自旋阈值; 区域自递归; 流量稳定机制

Class NumberTP393

1　引言

随着网络定位技术的不断推进,基于无线传感节点特性定位的技术也得到很大的发展[1]。由于网络节点定位技术是许多网络技术如采集、识别、监控等领域的基础性技术,因此成为当前研究过程的热点技术[2]。通过采用一定的算法提高定位过程中的准确性,降低定位过程中能量开支及提高无线传感节点在收发信号时的信噪比,成为了当前无线传感网定位技术中重要的研究热点[3]。

针对当前研究领域中存在的这些问题,人们采取了多种方式尽量提高各种算法的计算性能。GAO C等[3]提出可利用节点自身坐标递归特性,实现了在初步定位后采用线性收敛方程组的收敛特性,实现了节点的精确定位。但是,由于该种算法对初步定位的精确程度要求不高,导致方程组收敛的时间较长,影响了定位精度的进一步提高。CHEN D等[4]提出了一种基于多节点的联合定位方法,通过预先针对多个锚节点同时定位的方式,实现了网络中任意节点坐标的精确获取。然而,该算法需要预先对锚节点坐标进行存储,且锚节点的分布需满足均匀分布,当某个节点难以获得锚节点坐标或锚节点不满足均匀分布条件,则节点定位的精确程度将大大降低。Hao Xiaochen等[5]提出了一种基于自定位机制的节点定位算法,通过预先构建各个节点间的关联顺序,实现了在锚节点已知的情况下对节点的实时定位。但是,该节点需要通过sink节点对各个节点之间相对距离进行计算,在背景噪声复杂时定位的精确度也随之降低,此外由于该算法的定位效率较低,当网络中节点个数较多时将难以以高效的方式实现对节点坐标的精确捕获。

对此,本文提出了一种基于节点自旋阈值确认机制的无线传感网节点定位算法,通过构建节点定位自旋阈值,实现对节点的初步定位,同时采取流量稳定机制,实现数据在网络中的高效汇聚。最后通过NS2仿真平台对本文算法进行了仿真。

2　网络模型假设

由于当前的定位技术主要依托于无线传感网的定位性能而实现,因此当网络出现异常时将难以实现节点的精确定位,特别是当节点能量耗尽时将无法进行正常的定位过程[6],据此本文无线传感网做如下的假设:

1) 网络节点的分布满足均匀分布,即整个节点分布均不受人为因素的影响,处于自然分布状态[7];

2) 传感器节点由电池供电,当电源耗尽时整个定位过程也将终止[8];

3) 传感器节点的定位过程由无线射频信号作为定位介质,当仅当周围背景噪声的频率与无线射频信号频率近似时才产生严重的干扰效应[9];

4) 整个网络的核心成员为一具有无限处理能力的sink节点,该节点的缓存无限,电源能量不受限制[10]。

3　本文无线传感网节点定位算法

基于上述网络模型假设,本文提出了基于节点自旋阈值确认机制的无线传感网节点定位算法,整个算法由节点自旋阈值确认和优化传输两个部分所构成。

3.1节点自旋阈值确认

无线传感节点在定位过程中,任意一节点的自旋阈值主要由其周围节点到自身的位置关系决定的。对于某个节点而言,若该节点在进行旋转时与周围节点之间存在密切的信息交互关系,则该节点通过自旋获取的周围节点的信息也就越多,当获取信息的节点数量到达一定程度时,定位精确程度可以达到较高的水平。因此如果想通过基于无锚技术实现对节点的定位,则需要对待定位节点与周围节点间的关系特别是拓扑位移关系进行推断,综合考虑各个节点拓扑位移对待定位节点进行定位确认,可以计算得到待定位节点的精确坐标位置。

设i为某个待计算的节点,其周围两跳范围内的节点个数为ωi,则ωi满足如下的关系:

(1)

其中D为与i相邻的节点j的集合,显然i的孤立程度(即两跳范围内节点个数)越低,则ωi对应的数值也就越高。

不妨设i的初始坐标为ηij,则ηij满足如下的关系:

(2)

模型(2)计算得到的坐标反映了待定位节点与两跳范围内的节点之间的信息交互关系,当待定位节点不断以旋转方式对周围节点进行扫描时,可以通过模型(2)所示的公式实现对初始坐标的计算。然而由于单纯采用模型(2)对节点坐标进行计算有较大的局限性,特别是当前节点经过一次旋转扫描将难以实现对两跳范围内节点全覆盖时,所得的初始坐标将具有较大的误差。因此本文引入自旋阈值,采用该阈值对模型(2)所示的坐标进行修正,以便提高精确度。

待定位节点再进行一次扫描时,首先选取两跳范围内信号强度最强的节点作为基准节点,当待定位节点扫描其它节点时,将通过无线信号对比的方式获取各个节点到本节点的自旋阈值,采用排序的方式对各个阈值进行对比,自旋阈值E(r)通过模型(3)计算得到:

(3)

其中,T为待定位节点扫描周期,r为定位节点最大扫描频率,PC为待定位节点扫描出错概率,Pr为当前节点坐标精确度,ηij定义同模型(2)。

则节点i在经过r轮扫描之后的坐标μij满足如下表达式:

μij=ηijE(r-2)+E(r-1)

(4)

模型(2)也需要根据模型(3)进行修正,则更新之后的节点坐标满足:

(5)

相应参数同模型(1)、(2)所定义。

综合模型(4)、(5)可得待定位误差ψi满足如下的表达式:

(6)

显然通过模型(6)计算得到的定位误差ψi与扫描轮数呈现反比例关系,当扫描轮数较少时,将能有效地降低定位误差。对模型(6)求偏导数可得:

(7)

当仅当r=1时ψi取得最小值0,从模型(7)可以得到本文算法仅需要通过一轮扫描即可以将精度误差控制在0左右,大大降低了定位误差。

3.2优化传输

当定位误差降低在可控范围内之后,执行算法的数据优化传输,其详细步骤如下:

Step 1:统计节点的数据发送周期T,若在发送周期内均在sink节点的覆盖范围内扫描,则在每一次收到sink节点发送的数据上传指令后,启动两跳之内节点的搜寻并转Step 2;否则,转Step 3;

Step 2:按照模型(7)分别搜寻最佳中继节点,若计算所得位置未发生改变,则在下一刻收到sink数据分组之前将继续按照当前上传链路汇聚数据;否则,回到Step 1,并按模型(6)更新后的精度进行定位并发送数据,重新转Step 1;

Step 3:若节点的数据发送周期内,节点失效,则在节点失效前前重启定位过程的确认,算法结束。

4　仿真实验

本文采用NS2仿真平台对本文算法进行仿真,为验证本文算法的有效性,将与当前广泛使用的SWF节点定位算法[11～12]进行对比,在定位消息误差率、定位数据重启发送频率、扫描链路抖动时间、定位精度误差四个指标上进行对比。具体仿真参数如表1所示。

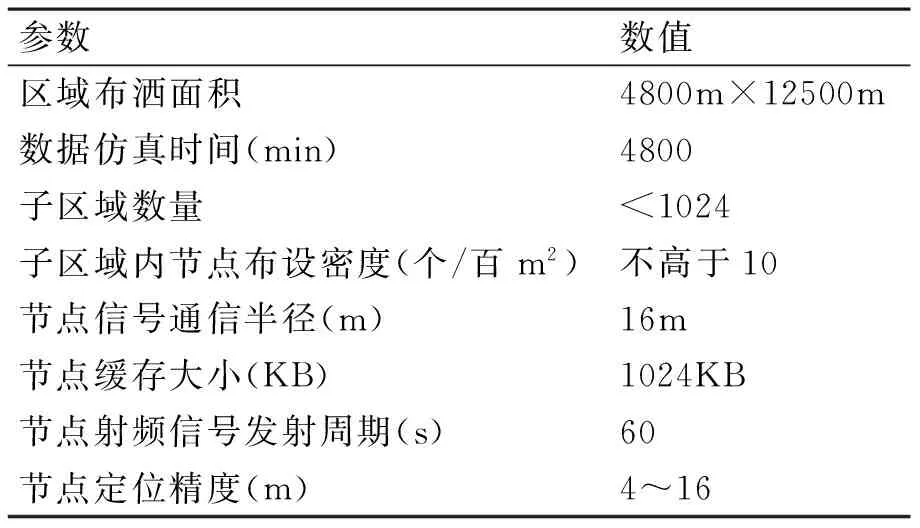
表1　仿真参数表

1) 定位消息误差率

图1显示了本文算法同对照组算法在定位消息误差率测试结果,从图中可以看到本文算法的对照组算法随着网络节点数量的增加均呈现不断增加的趋势,但是本文算法的定位消息误差率始终要低于对照组算法,这是因为本文算法引入了自旋阈值机制,能够通过多轮扫描有效的控制定位消息误差,因此能够降低定位消息传输过程中的出错概率,而对照组算法仅采取广播机制进行消息传输,当消息出现错误时将难以通过对错误的纠正实现对定位消息误差上的控制。

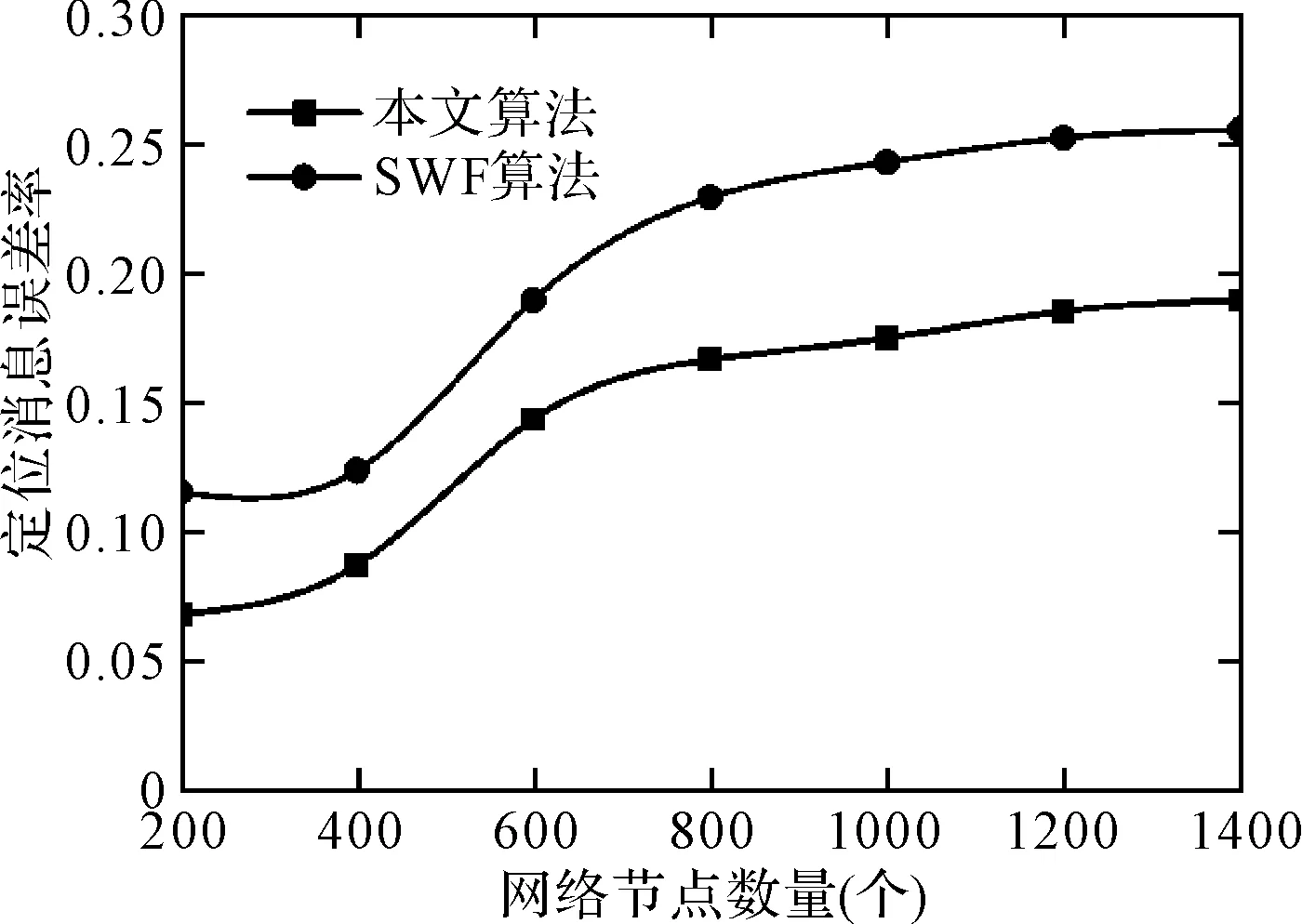
图1　两种算法的定位消息误差率测试结果

2) 定位数据重启发送频率

图2显示了本文算法同对照组算法在定位数据重启发送频率测试结果,从图中可以看到本文算法的重启发送频率始终要低于对照组算法,这是因为本文算法通过对两跳之内的节点均采用自旋扫描方式实现初步定位,一次定位的精度很高,因此无需通过多次重启定位数据发送的方式实现定位,而对照组算法由于对定位坐标的获取仅仅基于一个基准节点,需要通过多次定位实现数据重启发送,因而提高了算法的数据重启频率。

3) 扫描链路抖动时延

图3显示了本文算法同对照组算法在扫描链路抖动时延测试结果,从图中可以看到本文算法的扫描链路抖动时延始终要低于对照组算法,这是因为本文算法通过优化上传机制实现了最佳链路的筛选,因此能够有效的扫描过程中链路因背景噪声影响而发生的抖动效应,而对照组算法未引入任何抖动校验机制,当定位出现错误时难以有效降低扫描链路抖动时间。

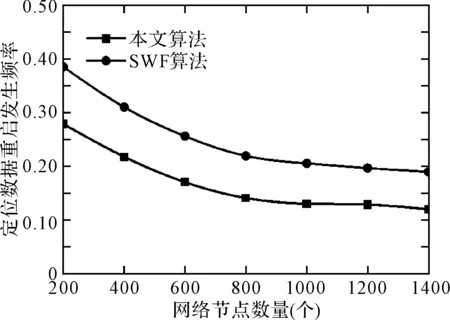
图2　各算法的定位数据重启发送频率测试

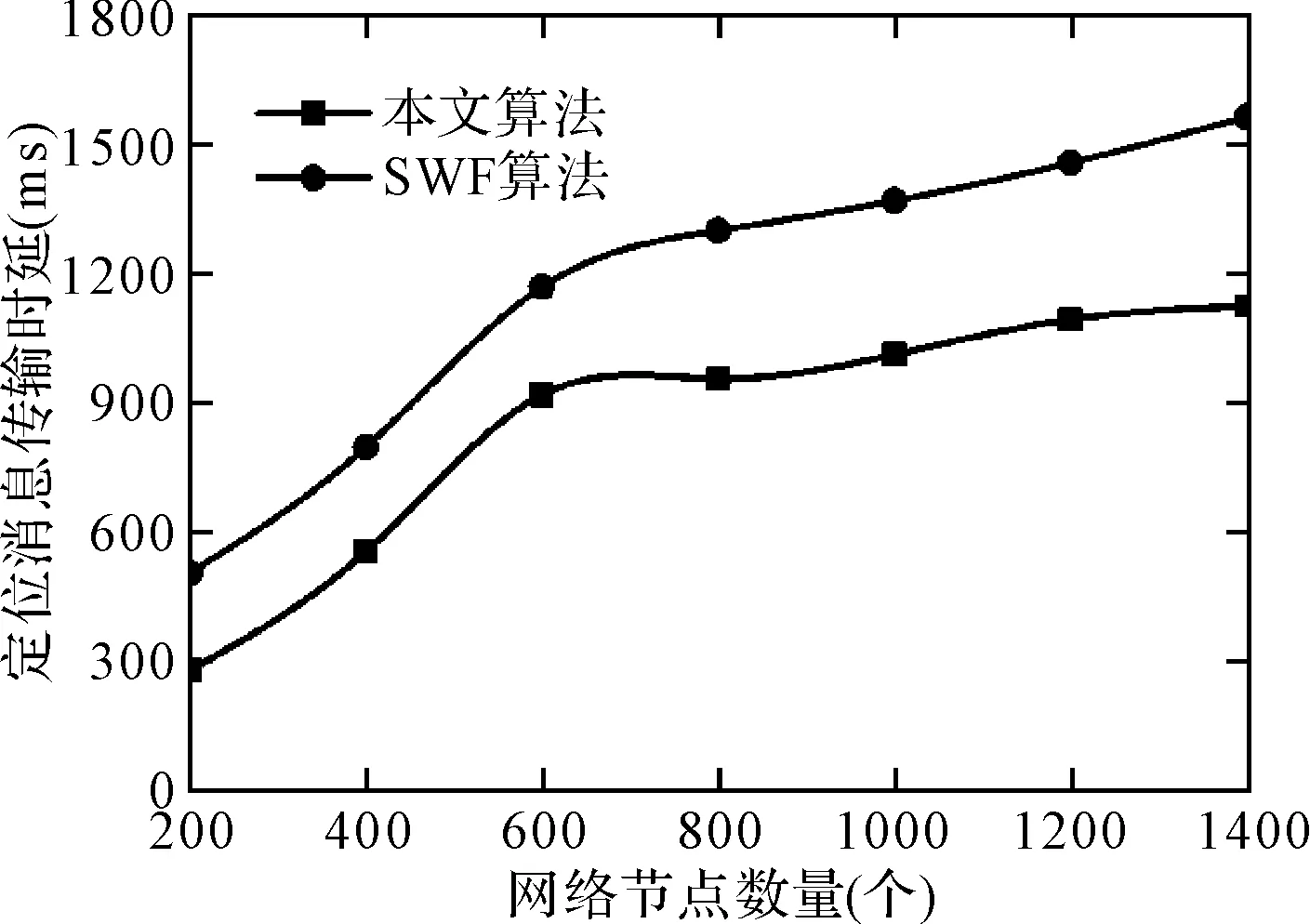
图3　两种算法的定位消息传输时延测试

4) 定位精度误差

图4显示了本文算法同对照组算法在定位精度误差上的对比,从图中可以看到本文算法的定位精度误差始终要低于对照组算法,这是因为本文算法通过引入扫描轮数实现了定位误差的精确化,因此能够有效的改善定位精度,而对照组算法的定位误差基于一次扫描成型,当定位出现错误时难以实现实时纠正导致定位精度误差高于本文算法。

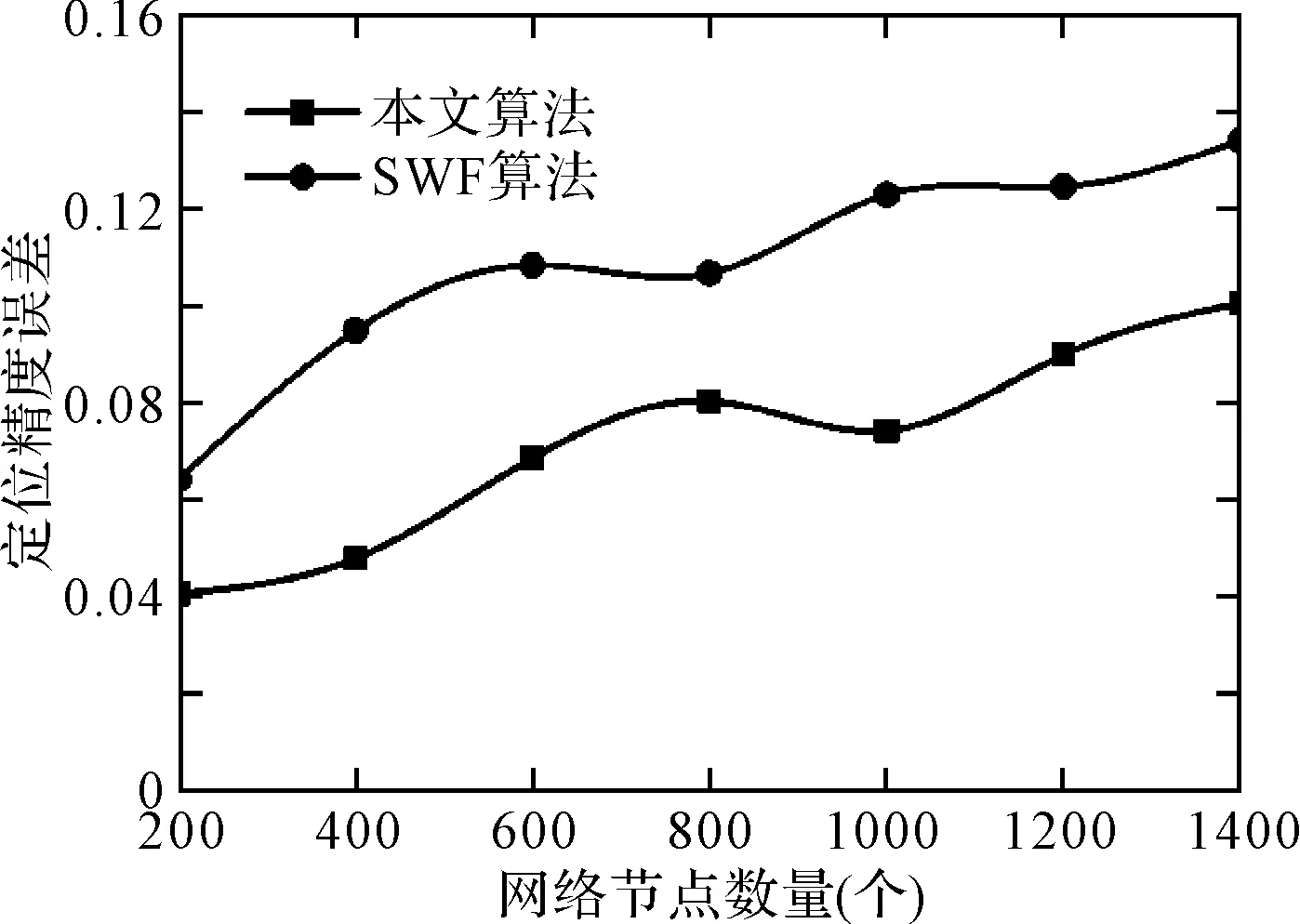
图4　各算法的定位精度测试

5　结语

本文提出了一种基于节点自旋阈值确认机制的无线传感网节点定位算法,在节点进行定位过程中采取扫描的方式对2跳范围内的节点进行阈值对比,实现对节点的一次定位。随后通过自旋阈值的引入,采取基于数值分析的方式对最佳扫描轮数进行了讨论,精确的计算出当定位误差精度很低时所需要的最佳扫描轮数,最后采取优化汇聚的方式,实现了数据的优化汇聚。仿真实验表明:与当前广泛使用的算法相比,本文算法在定位消息误差率、定位数据重启发送频率、扫描链路抖动时间、定位精度误差上具有明显的优势,对实践具有一定的指导意义。

下一步将通过引入立体定位机制,对多层网络节点的定位过程的误差精度进行控制,努力提高本文算法的适用范围,实现基于平面-立体综合定位的联合定位。

[1] ZHANG X, ZHU J. Identifying influential nodes in complex networks with community structure[J]. Knowledge-Based Systems,2013,42(13):74-84.

[2] 邬厚民.无线传感网络中能量和距离改良的节点定位算法[J].中国测试,2012,38(5):62-66.

WU Houming. Improved energy and distance improved node localization algorithm in Wireless Sensor Networks[J]. China Test,2012,38(5):62-66.

[3] GAO C, LAN X, ZHANG XG. A bio-inspired methodology of identifying influential nodes in complex networks[J]. PloS One,2013,8(6):667-732.

[4] CHEN D, LV L, SHANG M S, et al. identifying influential nodes in complex networks[J]. Physical A: Statistical Mechanics and its Applications,2011,391(4):1777-1787.

[5] Hao Xiaochen, Jia Nan, Liu Bin. Multi-path optimizing routing protocol based on predicting congestion for wireless sensor network[J]. Journal of Electronics & Information Technology,2011,33(5):1261-1265.

[6] Wang L, Geng X. A Community-driven Hierarchical Message Transmission Scheme in Opportunistic Networks[J]. Smart Computing Review,2011,1(1):85-94.

[7] Wang D, Zhang Q, Liu J C. Partial network coding: theory and application for continuous sensor data collection[C]//Proc. of the 14th IEEE International Workshop on Quality of Service,2012,35(10):93-101.

[8] ZHOU C, HE JW. A robust active queue management scheme for network congestion control[J]. Computers and Electrical Engineering,2013,39(1):285-293.

[9] 王文吉.基于能量因素的无线传感网络关键节点定位算法[J].电子与信息学报,2014,36(7):1728-1734.

WANG Wenji. Key node localization algorithm for wireless sensor networks based on energy factor[J]. Journal of Electronics and Information,2014,36(7):1728-1734.

[10] Habib M Ammari, Sajal K Das. A study of K-coverage and measures of connectivity in wireless sensor networks[J]. IEEE Transactions on Computers,2013,59(2):258-267.

[11] HA Le, Lijin, Yuanguo. A TCP Performance Enhancement Scheme in Infrastructure based on Vehicular Networks[J]. China Communications,2015,6(13):73-84.

Node Localization Algorithms for Wireless Sensor Network Node Based on Spin Threshold Confirmation Mechanism

ZHANG Linna

(Shaanxi Defence Vocational & Technical College, Xi’an710300)

In order to solve that the localization threshold in wireless sensor network link location process is difficult to determine, data link with the positioning accuracy of the exist problems such as excessive migration, this paper proposes a node localization algorithm for WSN node threshold confirmation mechanism based on the mechanism of spin. First, regional self recursive construction of node localization stability threshold, and node localization according to the threshold, in order to achieve the stability of the nodes in the cluster region search, then according to the characteristics of the process of data transmission, stable flow mechanism of choice for the optimization of data transmission, data in order to achieve efficient transmission convergence. Simulation experiments show that the algorithm in this paper can reduce the link stability consideration, to achieve the precise position of the optimization of data transmission, the node.

wireless sensor network, node localization, spin threshold, regional self recursion, stable flow mechanism

2016年2月7日,

2016年3月26日

张琳娜,女,硕士,讲师,研究方向:无线传感器网络与数学模型。

TP393

10.3969/j.issn.1672-9722.2016.08.033