一种改进的遗传算法在年度排课问题中的应用

王　璐　杨亚伟

(1.山东省质量技术监督教育培训中心　济南　250013)(2.山东电力工程咨询院有限公司　济南　250013)



一种改进的遗传算法在年度排课问题中的应用

王璐1杨亚伟2

(1.山东省质量技术监督教育培训中心济南250013)(2.山东电力工程咨询院有限公司济南250013)

论文深入分析了年度排课问题的特点,提出了一种基于改进遗传算法的求解方法。该方法通过分析适应度与编码之间的内在关系,对常规遗传算法的杂交和变异操作进行了改进,提出了基于子适应度的纵向基因杂交法和自适应变异策略等方法。仿真结果表明该改进的遗传算法相比于常规遗传算法在求解年度排课问题时性能有了较大的提升。

遗传算法; 年度计划; 排课问题; 自适应变异策略

Class NumberTP391.1; G433

1　引言

随着教育事业的发展和学校规模的增加,排课问题逐渐成为各类学校教学管理工作中的一个重点问题和难点问题[1]。排课问题是一个多约束、多目标的组合优化问题,是一个NP完全问题[2],在排课的过程中,需要综合考虑教师、教室、实验室、时间分配以及各种约束条件等多方面的因素[3]。随着计算机技术的发展,以遗传算法为代表的各种智能算法被应用到这类排课问题当中,并取得了不错的效果[4]。

目前对于排课问题的研究,绝大多数都集中在以高校排课为代表的周排课问题上,而对于年度排课问题的研究,则较为少见。

2　年度排课问题及其特点

年度排课问题是指以年为周期的排课问题,这类排课问题在各种培训机构中较为常见。以山东省质量技术监督教育培训中心为例,该中心每年年初会制定并发布该年度的培训计划,以便学员根据需要来选择培训课程。该培训计划中通常包含了本年度所要开展的培训课程及其时间、教室、实验室、教师、班主任(主要负责该课程培训期间的管理工作)等相关信息,是一个典型的以年为周期的排课问题。与普通高校的周排课问题相比,年度排课问题有如下特点:

1) 排课以一年为周期,以一天为最小时间片;

2) 每门课程的学员人数在排课时无法精确获得,只能根据以往经验来估计;

3) 对于课表优劣性的评判标准,与周排课问题有很多不同之处。

因此,在解决年度排课问题时,并不能完全照搬周排课问题的解决方案,而是需要针对年度排课问题的特点做一些改进和优化。

3　年度排课问题的数学模型

3.1模型中的硬约束条件

年度排课问题的硬约束条件与周排课问题的硬约束条件[5]类似,即

1) 同一时间,一个教室不能同时有一门以上的课程;

2) 同一时间,一个实验室不能同时有一门以上的课程;

3) 同一时间,一个教师不能同时有一门以上的课程;

4) 同一时间,一个班主任不能同时有一门以上的课程。

3.2模型中的软约束条件

由于年度排课问题自身的特点,其软约束条件与周排课问题相比有很多不同之处。下面是本文模型中的具体软约束条件。

3.2.1均匀度

由于整个培训中心一年的工作安排都与该年度的培训计划密切相关,因此年度培训计划要求有良好的均匀度,以使全年的工作可以合理而均匀的分布,从而避免某些时段过于繁忙而某些时段过于清闲。

均匀度是表示点集在空间中分布均匀性的一个参数[6]。均匀度的表示方法有很多,但多数方法的本质都是利用方差来计算均匀度[7]。对于课表的时间均匀度问题,可以看做是一个一维空间的点集均匀度问题,利用方差来表示其均匀度系数α的方法如下:

(1)

在利用式(1)计算年度课表的时间均匀度时,其时间段i可以选择以天为单位,也可以选择以周为单位。由于以天为时间段会大大增加程序的计算量,并且从实际角度来考虑也没有明显的优势,因此本文选择以周为时间段来进行课表均匀度系数的计算。

一般认为,利用式(1)得到的均匀度系数越小,表示其均匀度越好。然而通过一些具体实例的研究发现,在某些情况下,并不是得到的均匀度系数越小,其均匀度就越好。表1给出了两个课表工作量分布的实例,利用式(1)计算得到两个课表的均匀度系数都是5,然而通过观察发现,课表1的工作量时间分布要比课表2更为均匀,因此仅仅利用式(1)来衡量课表的均匀度并不完全合适。

表1　课表工作量实例

造成上述问题的原因在于,式(1)中计算的方差只能体现每个时间段工作量分布的离散程度,而不能体现整个时间周期内工作量的分布趋势。为了弥补这个缺陷,本文定义一个均匀分布系数β来表示工作量的整体分布趋势:

(2)

(3)

利用式(2)得到的分布系数β值越小,表示其工作量的整体分布越均匀。利用式(2)来计算表1中两个课表实例的均匀分布系数β,课表1的分布趋势系数为3.54,课表2的分布趋势系数为14.58,由此可以看出均匀分布系数β能够很好地反应工作量的整体分布趋势是否均匀。

均匀度系数α和均匀分布系数β分别从个体离散程度和总体分布趋势两个方面来体现了课表的均匀度,两个参数可以起到很好的互补作用,因此关于年度课表的均匀度PA,本文用如下方式表示

PA=C1α+C2β

(4)

其中,C1和C2是常数,用来设置均匀度系数α和均匀分布系数β在均匀度计算时的权重。

有了均匀度的表示方法,便可以对课表的均匀度进行计算。本模型中课表的均匀度计算由以下几个部分组成:

1) 全部课程的总体均匀度。

2) 每种类型课程的均匀度。本模型中,按照课程类型,可以将全年所有培训课程分为几大类,对于每一类课程而言,应尽量均匀分布,以使本类课程的学员可以在全年的各个阶段都能够进行学习。

3) 每名教师的课程均匀度。对于每名教师而言,其教学任务也应该均匀地分布在全年各个时段,以避免某些时间过于繁忙。

4) 每名班主任的课程均匀度。对于每名班主任而言,其所负责的课程也应均匀的分布在全年各个时段,以避免某些时段过于繁忙。

3.2.2周末及节假日的占用情况

对于占用周末及节假日的问题,不同的模型可能有不同的要求,在本模型中,希望在满足其他要求的情况下,周末及节假日占用率越低越好。周末及节假日占用率PH可利用下列公式计算

(5)

其中,W是课表所占用的周末总天数,H是课表所占用的节假日总天数,W0是该年度中周末的总天数,H0是该年度中节假日的总天数,C1和C2分别是周末及节假日的权重系数,其值越高表示越不想被占用。

3.2.3备用教室

在本模型中,由于在制定计划时并不能提前知道每门课程的精确学员人数,因此只能根据预估的学员人数来选择教室,这样做必然存在实际学员人数超过教室容量的风险。为了降低这种风险,我们希望在满足其他要求的情况下,能够尽可能为每门课程留有一个容量更大的备用教室。备用教室的配备情况可以用备用教室配备率PC来表示:

(6)

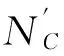
3.2.4班主任及教师的工作量平均分配

在本模型中,每门课程一般都有多个班主任和教师可供选择,因此我们希望每个班主任和教师的工作量可以尽量平均分布,避免某些班主任和教师的工作量过多,而某些班主任和教师的工作量过少。班主任和教师的工作量平均分配程度可以用平均分配系数PD来表示:

(7)

其中,n是班主任的总数,Ei是第i名班主任的总工作量,S是所有课程的总工作量。

4　改进遗传算法的设计方案

4.1编码

本文采用排课问题中通常使用的十进制矩阵编码方式来进行编码,具体编码方式如表2所示。其中,每门课程的开始日期用3位十进制数表示,其余4项均用2位10进制数表示,每个课程的编码共计11位。例如编码10003010401,代表该课程在该年度第100天开始培训,培训用教室ID为03,培训用实验室ID为01,课程班主任ID为04,授课教师ID为01。将所有课程的编码依次罗列,便组成了整个课表的矩阵编码。

表2　十进制矩阵编码方式

4.2初始种群

初始种群一般采用随机生成的方式产生,但是对于排课问题,利用随机方式生成的初始种群中往往存在较多不满足模型硬约束条件的个体,在这种情况下算法的性能会受到很大的影响。为了提高算法的搜索速度,本文在利用随机方式生成初始种群后,会对初始种群中的个体进行硬约束条件检测,当发现不满足模型硬约束条件的个体时,会重新生成该个体直至所有个体均满足模型的硬约束条件。

4.3适应度计算

个体的适应度主要从均匀度、周末及节假日占用情况、备用教室配备情况以及工作量平均分配情况等几个方面来衡量。前文已经给出了上述每种子适应度的具体模型和计算方法,在计算个体的总体适应度时,需要为每个子适应度设置一个权重值,以按照具体需求来调节每种子适应度的权重。本文中子适应度的权重值设置如表3所示。对于不满足硬约束条件的个体,其适应度为0。

4.4复制

本文采用适应度比例选择法来作为遗传算法中的复制方法,该方法依据个体的适应度进行选择,适应度越高的个体被复制的概率就越大。

表3　子适应度权重值

4.5基于子适应度的纵向基因杂交法

杂交是种群中不同个体之间通过交换对应的基因来实现的,是遗传算法中产生新个体的主要手段[8]。对于排课问题而言,通常将每门课程的安排看做是一个基因,在进行杂交操作时,在随机选择杂交的个体之后,只需要将杂交双方该范围内的课程安排互换即可。

然而,通过实际测试发现,这种杂交方法在解决年度排课问题时效果并不理想。通过分析发现,个体的适应度大小与本文所采用的十进制矩阵编码之间存在一定的关联:

1) 课表均匀度、以及周末及节假日占用率,与整个课表的时间安排关系最为密切,即表2编码中的第2列数据;

2) 教师的课程均匀度及教师的工作量平均度,与教师的整体安排关系最为密切,即表2编码中的第6列;

3) 班主任的课程均匀度及班主任的工作量平均度,与班主任的整体安排关系最为密切,即表2编码中的第5列;

4) 备用教室配备情况,与教室的整体安排关系最为密切,即表2编码中的第3列。

因此,在杂交操作时互换个体中对应的课程安排,即互换表2编码中对应的某些行,很难有效的提高个体的适应度。为了解决这一问题,本文采用一种基于子适应度的纵向基因杂交法,该方法首先按照表3中的各项子适应度分别对种群中的个体进行排序,然后对于每项子适应度,选择种群中该子适应度最低的个体,将其与该子适应度最为相关的纵向基因替换为种群中该子适应度最高的个体中的对应基因。基于子适应度的纵向基因杂交法的流程图如图1所示。

在其它条件完全相同的情况下,基于子适应度的纵向基因杂交法与常规杂交法的实际运行结果如图2所示。通过图2可以看出,基于子适应度的纵向基因杂交法能够大大改善算法的性能。

图1　基于子适应度的纵向基因杂交法流程图

图2　基于子适应度的纵向基因杂交法与常规杂交法对比

4.6自适应变异策略

种群中进行变异的基因数量B由变异概率变Pm来决定,即

(8)

其中,M为种群中个体的数量,L为个体中携带的基因数量。

变异概率是一个敏感参数,其值对算法的运行结果有较大的影响。增大变异概率,能够增强物种的多样性,但变异概率过大,会降低算法的收敛速度;减小变异概率,则会影响算法的搜索范围,不利于得到全局最优解[9]。本文模型中变异概率取值对结果的影响如图3所示。

通过图3可以看出,变异概率不能设得过大或者过小,而是应当在一个适当的范围内取值。

常规遗传算法中将变异概率设置为一个常数,因而无法根据每个个体的特点来执行不同的变异策略。本文采用一种自适应变异策略[10],其在执行变异操作时,会根据不同个体的各项子适应度的大小来决定变异概率的取值,具体方法为:

图3　变异概率对结果的影响

1) 在对课程的日期安排进行变异操作时,变异概率根据课程均匀度以及周末及节假日占用率两项子适应度的值确定;

2) 在对课程的教室安排进行变异操作时,变异概率根据备用教室配备情况的子适应度值确定;

3) 在对课程的班主任安排进行变异操作时,变异概率根据班主任的课程均匀度以及班主任工作量平均度两项子适应度的值确定;

4) 在对课程的教师安排进行变异操作时,变异概率根据教师的课程均匀度以及教师工作量平均度两项子适应度的值确定。

群体中第i个个体的自适应变异概率Pmi的取值与相关子适应度的关系如下:

(9)

通过设置变异概率取值上限Pmax、取值下限Pmin以及基准概率Pm,可以让不同个体根据其相关子适应度的大小来改变其变异概率,当相关子适应度较大时,变异概率取值介于Pmin和Pm之间,当相关子适应度较小时,变异概率取值介于Pm和Pmax之间。

为了验证自适应变异策略的性能,本文分别对普通变异策略和自适应变异策略进行了仿真测试,结果如图4所示。通过图4可以看出,相比于普通变异策略,自适应变异策略性能更优。

4.7中止条件

遗传算法是一个反复迭代的过程,每次迭代期间,都要执行适应度计算、复制、杂交、变异等操作,直至满足终止条件。遗传算法常用的终止方法有三种,即最大迭代次数设定法、最小方差设定法以及适应度变化趋势观察法。本文中选择最大迭代次数法,迭代次数设置为1000。

图4　普通变异策略与自适应变异策略对比

5　仿真结果

本文选择山东省质量技术监督教育培训中心某年的年度培训计划为仿真测试数据,该仿真测试数据的相关要素如表4所示。

表4　测试数据相关要素

仿真测试时遗传算法的相关参数设置如表5所示。

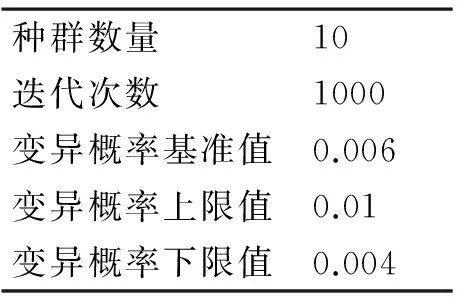
表5　遗传算法参数设置

图5　仿真结果

分别对本文所给的改进遗传算法和普通遗传算法进行100次仿真测试,然后将所得结果取平均值,最终结果如图5所示。通过图5可以看出,在解决年度排课问题时,本文所给的改进遗传算法与普通遗传算法相比在性能上有了较大的提升。

[1] 张赫男,张绍文.采用改进的混合遗传算法求解高校排课问题[J].计算机工程与应用,2015,51(5):240-246.

ZHANG Henan, ZHANG Shaowen. Improved hybrid genetic algorithm for university timetabling problem[J]. Computer Engineering and Applications,2015,51(5):240-246.

[2] 江齐,兰竞.遗传算法在排课问题中的运用[J].重庆大学学报:自然科学版,2005,28(11):58-61.

JIANG QI, LAN Jing. Application of the Genetic Algorithm in Timetable Problem[J]. Journal of ChongQing University(Natural Science Edition),2005,28(11):58-61.

[3] 李红蝉,朱颢东.采用十进制免疫遗传算法求解高校排课问题[J].系统工程理论与实践,2012,32(9):2031-2036.

LI Hongchan, ZHU Haodong. Decimal immunization GA used to solve UTP[J]. Systems Engineering — Theory & Practice,2012,32(9):2031-2036.

[4] Edmund K B, Sanja p. Recent research directions in automated timetabling[J]. European Journal of Operational Research,2002,7:18-27.

[5] 滕姿,邓辉文,杨久俊.基于遗传算法的排课系统的设计与实现[J].计算机应用,2007(12):199-204.

TENG Zi, DENG Huiwen, YANG Jiujun. Courses arrangement system base on genetic algorithms[J]. Journal of Computer Applications,2007(12):199-204.

[6] 罗传文.点空间分析——分维与均匀度[J].科技导报,2004,196(10):51-54.

LUO Chuanwen. Point spatial analyses-fractal dimension and uniform index[J]. Science & Technology Review,2004,196(10):51-54.

[7] 聂峻.均匀度理论及其应用研究[D].成都:成都理工大学硕士学位论文,2011:1-2.

NIE Jun. Research on Uniformity Theory and Applications[D]. Chengdu: Chengdu University of Technology,2011:1-2.

[8] 王小平,曹立明.遗传算法——理论、应用与软件实现[M].西安:西安交通大学出版社,2002:34-37.

WANG Xiaoping, CAO Liming. Genetic algorithms: theory, application and software implementation[M]. Xi’an: Xi’an Jiaotong University Press,2002:34-37.

[9] 云庆夏.进化算法[M].北京:冶金工业出版社,2000:70-72.

YUN Qingxia. Evolutionary algorithms[M]. Beijing: Metallurgical Industry Press,2000:70-72.

[10] 朱灿,梁昔明.一种多精英保存策略的遗传算法[J].计算机应用,2008,28(4):939-941.

ZHU Can, LIANG Ximing. Novel genetic algorithm with multi-elitist preservation method[J]. Journal of Computer Applications,2008,28(4):939-941.

Application of an Improved Genetic Algorithm in Annual Timetable Problem
WANG Lu1YANG Yawei2
(1. Shandong Education Training Center of Quality and Technical Supervision, Jinan250013)

(2. Shandong Electric Power Engineering Consulting Institute Co ltd, Jinan250013)

Annual timetabling problem was analyzed detailedly, and an improved genetic algorithm was proposed to solve this problem. Longitudinal gene crossover method based on sub-fitness and adaptive aberrance strategy was proposed by analyzing the intrinsic relation between fitness and code. Simulation results indicated that this improved genetic algorithm can solve annual timetable problem more effective than common genetic algorithm.

genetic algorithm, annual plan, timetable problem, adaptive aberrance strategy

2016年2月10日,

2016年3月24日

王璐,女,硕士,工程师,研究方向:特种设备培训。杨亚伟,男,硕士,工程师,研究方向:电厂仪控系统的设计与工程管理

TP391.1; G433

10.3969/j.issn.1672-9722.2016.08.047