基于噪声最优航迹的飞行程序优化方法研究

吕宗平　陈雪蕊　徐　涛,

(1.中国民航信息技术科研基地　天津　300300)(2.中国民航大学计算机科学与技术学院　天津　300300)



基于噪声最优航迹的飞行程序优化方法研究

吕宗平1陈雪蕊2徐涛1,2

(1.中国民航信息技术科研基地天津300300)(2.中国民航大学计算机科学与技术学院天津300300)

机场建设促进了周边地区的经济发展,同时不可避免的带来了航空噪声。为有效控制航空噪声,基于不同飞行程序将航迹进行聚类分析,提出飞行程序的噪声最优航迹的概念。以噪声最优航迹为指导优化飞行程序,使航班执行优化后的飞行程序能避免飞过人口稠密区,从而降低航空噪声影响。以首都机场为例进行实验验证,将优化后的飞行程序导入INM(Integrated Noise Model)中,计算噪声敏感区的噪声值以及不同噪声区间内的人口和面积,并绘制噪声等值线图。实验表明,所提出的基于噪声最优航迹的飞行程序优化方法具有可行性,能有效降低航空噪声影响,可为减噪飞行程序设计提供理论依据。

飞行程序; 机场噪声; 航迹聚类; 噪声最优航迹

Class NumberTP391

1　引言

中国民航的迅猛发展令世界瞩目,但是,不断新建、扩建机场和持续增长的航空运输量,也使得困扰中国民航已久的机场噪声问题愈发严重。因此,科学合理地控制机场噪声显得尤为重要。

目前,关于机场噪声的控制措施有一定的成果:国际民航组织ICAO(International Civil Aviation Organization)颁布的《飞机噪声管理的平衡做法指导》(Doc 9829 AN/451)[1]中提出了减噪的四个措施,分别是减少噪声源,土地使用规划和管理,减噪运行程序和运行限制。闫国华等研究了ICAO噪声严格度对中国机队的影响[2],从降低噪声源,淘汰老式飞机方面研究如何降噪。冯霞等研究了基于土地分类的机场噪声评价限值标准比较[3],为机场周边的土地规划提供方案,但并没有提出具体的降噪措施。Prats,X和Wijnen, R.A.A等分别以降低人口烦恼度与睡眠干扰率为目标[4～5],优化离港飞行航迹,为飞行程序的优化提供了理论基础。费代祥、闫国华等研究了大角度进近减噪程序[6～7],其减噪效果可观,但对跑道的寿命以及飞机起落架的寿命都有极大影响。戴福青等研究了基于性能的导航技术PBN(Performance Based Navigation)的中小机场终端区飞行程序优化[8],能够缓解管制员的工作负荷,提高航空公司运行效益,但没有对降低噪声进行研究。黑妍茹等研究了航空噪声及减噪声程序[9],介绍了减噪声程序的定义,但未对现行飞行程序提出优化措施。Gągorowski,A研究了连续下降进近程序CDA(Continuous Descent Approach)的噪声计算方法[10],并验证了CDA程序可降低机场噪声影响。

然而,更换更安静的航空器需要高昂的成本,土地规划对已建成且在运营中的机场降噪效果有限,运行限制会制约机场运行能力的充分发挥,因此本文基于利用代表点聚类(Clustering Using Representatives,CURE)[11]算法将执行同一飞行程序的运行航迹聚为一类,将该类航迹分别导入INM中计算同一飞行程序的不同运行航迹的噪声影响,并定义飞行程序的噪声最优航迹。在此基础上,以噪声最优航迹为指导优化飞行程序的航路点使航班侧向绕过人口密集区域,从而降低航空器的噪声影响,最后以北京首都国际机场为例进行了应用分析。

2　基于航迹聚类的噪声最优航迹发现

航迹决定机场周围噪声的分布模式,民用机场的运营每天都会产生大量的航迹数据,每年将积累海量的历史航迹数据。每一条航迹均为执行特定的飞行程序而来,因此将航迹根据其所执行的飞行程序进行聚类,分析其噪声影响。

2.1基于CURE的航迹聚类算法

航迹数据是由空管部门使用雷达监测设备获得的飞机运行中的经度、纬度和高度等数据。为将执行同一飞行程序的航迹聚为一类,首先分析航迹相似性度量方法。文献[12]基于航迹点法向距离的方法来度量两条航迹之间的相似性,并定义航迹间的相似性矩阵RT,如式(1)所示:

(1)

其中dni表示第n条航迹与第i条航迹的航迹点的法向距离。考虑到K-Means聚类算法[13]随机初始化聚类中心,容易导致聚类结果陷入局部最优,因此本文使用基于层次的CURE聚类算法,在聚类过程中使用中心点和多个代表点来表示聚类,表1给出了基于CURE的航迹聚类算法。

表1　基于CURE的航迹聚类算法

注:Ci代表聚类结果中第i类航迹集,avei代表Ci的簇中心航迹,Rei代表Ci的代表航迹集,每一个Rei均有r条航迹,其中i∈{1,2,…,k}。

2.2飞行程序运行航迹的噪声水平显著性差异分析

通过航迹聚类将执行同一飞行程序的航迹聚为一类,然而由于飞行员的飞行技术、飞机性能、天气状况等因素,使得即使执行同一飞行程序的航迹也不是完全相同,而是呈现一定的发散性。航迹决定机场周围噪声的分布模式,因此为了检验执行同一飞行程序的不同航迹具有显著性差异的噪声水平,本文定义两个航班执行同一飞行程序带来的噪声影响存在显著差异性的评价指标:

(2)

其中ti和tj分别是执行同一飞行程序的航迹中第i和第j个航班的航迹,m∈{1,2,…,num}是噪声敏感点的编号,num是机场周围噪声敏感点的个数,Lm(ti)表示第i条航迹对第m个噪声敏感点的噪声影响值。式(2)的直观含义是:同一飞行程序的两条运行航迹产生具有显著性差异的机场噪声的充要条件是在机场周边的噪声敏感点中至少存在一个噪声敏感点使得同一飞行程序的两条运行航迹在此敏感点的噪声差值大于5dB。之所以定义为5dB,是由于机场噪声受到多个因素的影响[14],对噪声敏感点增加考虑背景噪声,如车辆噪声、生活噪声(广场舞音乐、动物叫声等)、天气因素(雷声,雨声)等,则5dB差值内可认为两个噪声事件不具有显著性差异,而当噪声差值超过5dB时,两个噪声事件具有显著性差异。采用统计方法T-test进行差异性检验,结果表明同一飞行程序的运行航迹产生的噪声影响是存在显著性差异的。

2.3飞行程序的噪声最优航迹

由2.1节航迹聚类算法将执行同一飞行程序的航迹聚为一类,根据2.2节飞行程序运行航迹的噪声水平显著性差异分析得到:不同航班执行同一飞行程序产生的航迹具有发散性,且这些航迹的噪声影响具有显著性差异。那么,必然存在一条航迹,使得机场周边的噪声敏感点受到的噪声影响最小,则称这条航迹为该飞行程序的噪声最优航迹。为量化计算飞行程序的噪声最优航迹,定义一条航迹的综合噪声评价量为

E(ti)=E1(ti)+E2(ti)+…+Enum(ti)

(3)

其中num表示噪声敏感点个数,Ej(ti),j∈(1,2,…,num)表示第i条航迹对第j个噪声敏感点的综合噪声影响,且:

(4)

其中Lj(ti)表示第i条航迹在第j个噪声敏感点产生的噪声值,将其除以100(默认最大噪声值为100分贝)进行数据归一化操作,Num(Lj(ti)>70dB)和Arear(Lj(ti)>70dB)分别表示Lj(ti)>70dB的人口数和区域面积,Totalj(Pnum)和Totalj(arer)分别为第j个噪声敏感点的总人口数和总区域面积。航迹i在噪声敏感点j处产生的噪声值、受噪声影响的人口数以及区域面积均利用INM[15]计算获得。

综上所述,对于执行某一飞行程序的所有航班的航迹集合T={t1,t2,…,tz},其中z为执行同一飞行程序的航班总数,其噪声最优航迹tbest为

tbest=argminE(ti),其中ti∈T

(5)

式(6)的直观含义是:某一飞行程序的噪声最优航迹tbest是航迹集合T中满足综合噪声评价量最小的那条航迹。

3　基于噪声最优航迹的飞行程序优化

3.1飞行程序优化流程

飞行程序设计需要综合考虑超障安全、提高经济效率和减少噪声对周边社区的影响。通常航行服务部门规定的离场飞行程序设计方法可以保证超障安全,但在运行的经济性和航空噪声影响方面尚无具体可参照的方法与标准。本文以降低机场周边社区的航空噪声为目标,优化飞行程序的设计。参照第2节的思路,在执行同一飞行程序的航班产生的航迹簇中搜索一条噪声最优航迹作为标杆,并以此优化现有飞行程序的航路点坐标,使得优化后的飞行程序避开人口稠密区,其流程如图1所示。

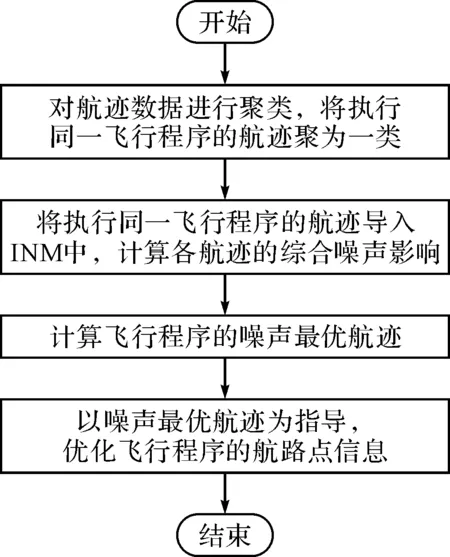
图1　基于噪声最优航迹的飞行程序优化流程图

3.2飞行程序的航路点优化方法

通过计算获得飞行程序的噪声最优航迹tbest,其可用航迹点序列表征:

tbest={p1,p2,…,pi,…,pl}

(6)

其中:pi表示tbest中第i个航迹点,i∈(1,2,…,l)为航迹点编号,l为航迹点总数。

每一个航迹点pi定义为二维向量:

pi={long,lat}

(7)

其中:long,lat分别表示第i个航迹点的经度和纬度,分别用pi(long),p(lat)表示。

标准飞行程序可用航路点的数据集表征:

Pro={w1,w2,…,wt,…,wo}

(8)

其中:wi表示Pro的第i个航路点,i∈(1,2,…,o)为航路点编号,o为航路点总数。

每一个航路点wi也定义为二维向量:

wi={long,lat}

(9)

其中:long,lat分别表示第i个航路点的经度和纬度,分别用wi(long),wi(lat)表示。

噪声最优航迹在保证飞行安全的前提下可使航空噪声的影响最小。因此以噪声最优航迹为指导,分别计算噪声最优航迹上距离飞行程序各航路点最近的航迹点,依次优化飞行程序各个航路点。其核心问题是如何计算两个由经纬度表示的点之间的距离,为解决此问题,给出一种由两点的经纬度计算两点之间距离的公式:

(10)

其中pi(long)和pi(lat)分别为第i个点的经度和纬度,表2给出了飞行程序航路点的优化算法。

表2　基于噪声最优航迹的飞行程序优化算法

根据表2所述算法可以计算出优化后飞行程序的各个航路点,为更加直观地表示飞行程序航路点的优化方法,图2给出了基于噪声最优航迹优化飞行程序航路点的示意图。

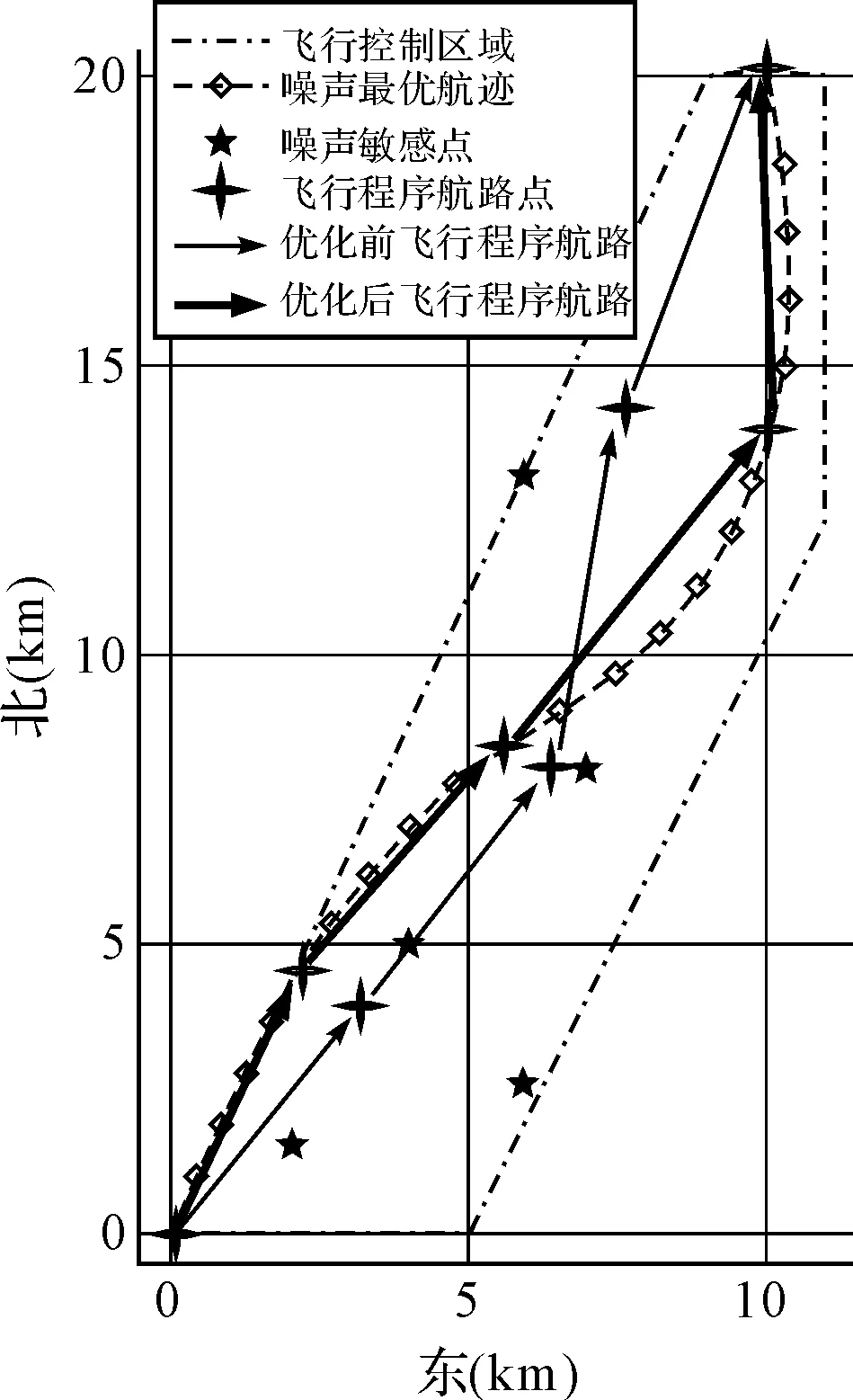
图2　基于噪声最优航迹的飞行程序航路点优化

根据图2可知,优化后的飞行程序航路点避开了噪声敏感点,且仍在飞行控制区域内,在保证飞行安全的同时降低了噪声敏感点的综合噪声影响,因此该方法可以有效降低机场周边噪声敏感点的综合噪声影响。

4　实验结果与分析

为了验证基于噪声最优航迹的飞行程序优化方法的有效性,以北京首都国际机场的运行航迹数据以及周边的东马各庄、西杜兰、南法信、天竺村、吴各庄、管头、南半壁店、樱花园等典型噪声敏感点进行实例分析,设计了以下三组实验。

【实验一】航迹聚类分析。实验采用北京首都国际机场2015年的航迹数据,选取机场单条跑道一周的离港航迹进行试验。为保证航迹长度大致相同,以跑道中心为圆心,截取半径为65km内的航迹数据。根据CURE算法的特性,当聚类个数为8,代表点个数为7时,航迹聚类效果最好,结果如图3所示。

图3　跑道36R上一周所有航班的航迹聚类结果

由图3可知,每一簇航迹簇内都很相似,簇间都有一定差别,这是由于簇内航迹执行同一飞行程序,而簇间航迹执行不同的飞行程序。查找对应的航迹所在的跑道标准离场程序图,如图4所示。对比图3和图4可知聚类结果符合标准离场飞行程序的设计要求,说明航迹聚类结果是正确合理的。

图4　首都机场36R跑道的标准离场飞行程序图

【实验二】飞行程序运行航迹的噪声分析。实验采用实验一聚类结果中的一簇航迹进行试验,如图5所示。

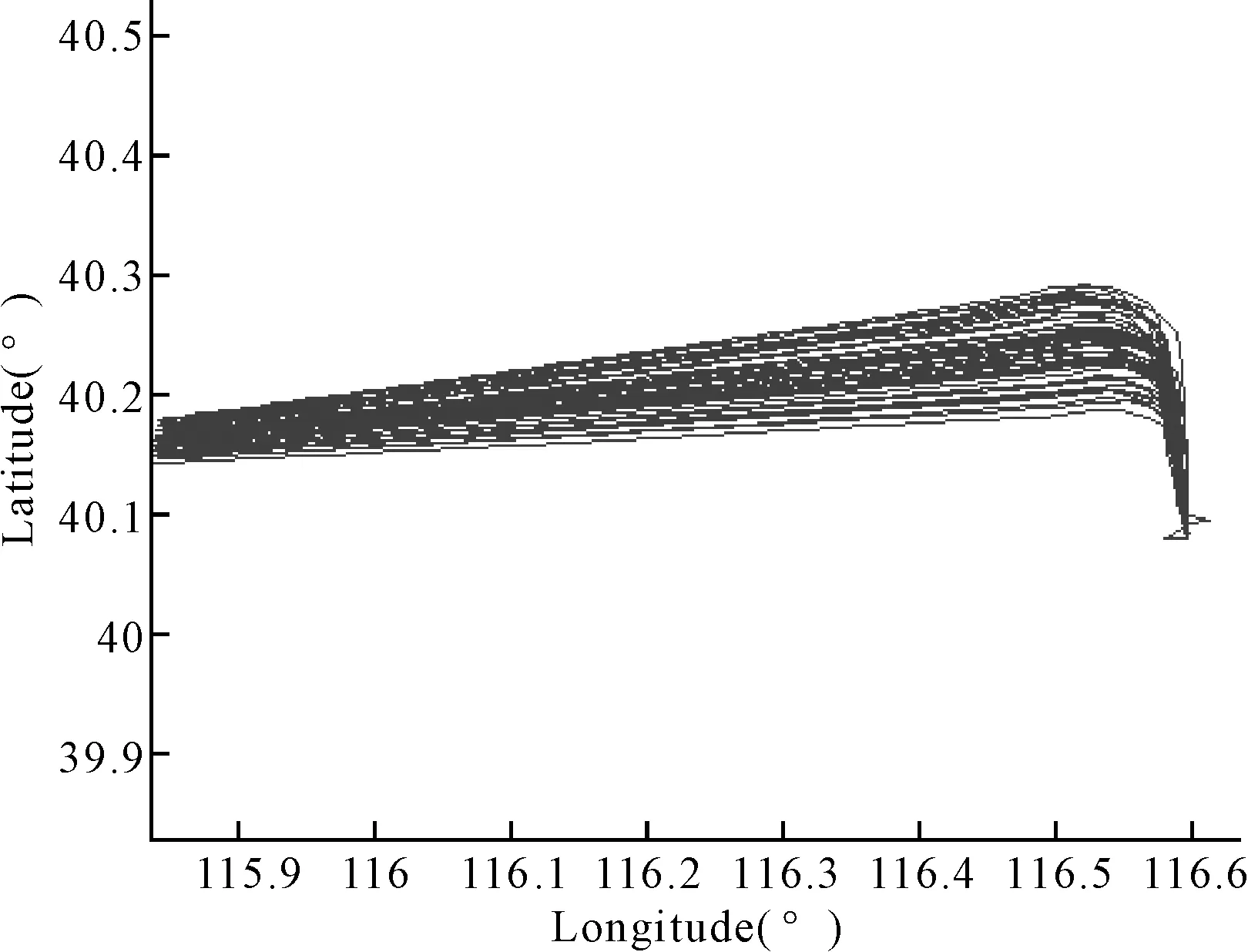
图5　一周内执行同一飞行程序的运行航迹

图5为一周内所有执行同一飞行程序的运行航迹信息,该簇航迹共有670条航迹,将这些航迹分别导入INM中,计算航迹对机场周边各个噪声敏感点的噪声影响大小,以及受噪声影响的人口数和面积。根据2.2节两条航迹的噪声存在显著差异性的评价指标,采用统计方法T-test进行检验,其检验结果如表3所示。

表3　T-test检验结果

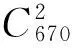
【实验三】基于噪声最优航迹的飞行程序优化方法的效果分析。实验采用首都机场周边八个典型的噪声敏感点,对其距离以及人口分布进行了实际测量和调查,统计结果如表4所示。

表4　首都机场典型噪声敏感点的人口与噪声水平统计

表4中的八个噪声敏感点主要集中在跑道端两侧,受飞机起飞带来的航空噪声影响比较严重。通过分析北京首都国际机场的历史航迹以及飞行程序数据库编码,确定每条飞行程序飞越的航路以及其主要影响的噪声敏感点,统计结果如表5所示。

表5　飞行程序主要影响区域统计

根据本文提出的基于噪声最优航迹的飞行程序优化方法计算表5中每条飞行程序对应的噪声最优航迹,以噪声最优航迹为标杆优化飞行程序的航路点,使优化后的飞行程序避开人口稠密区域。将优化前后的飞行程序分别导入INM中,计算飞行程序的计权等效连续感觉噪声级(Weighted Equivalent Continuous Perceived Noise Level,WECPNL)以及不同噪声区间内的噪声影响人口和面积。图6所示为飞行程序优化前后的噪声等值线图。

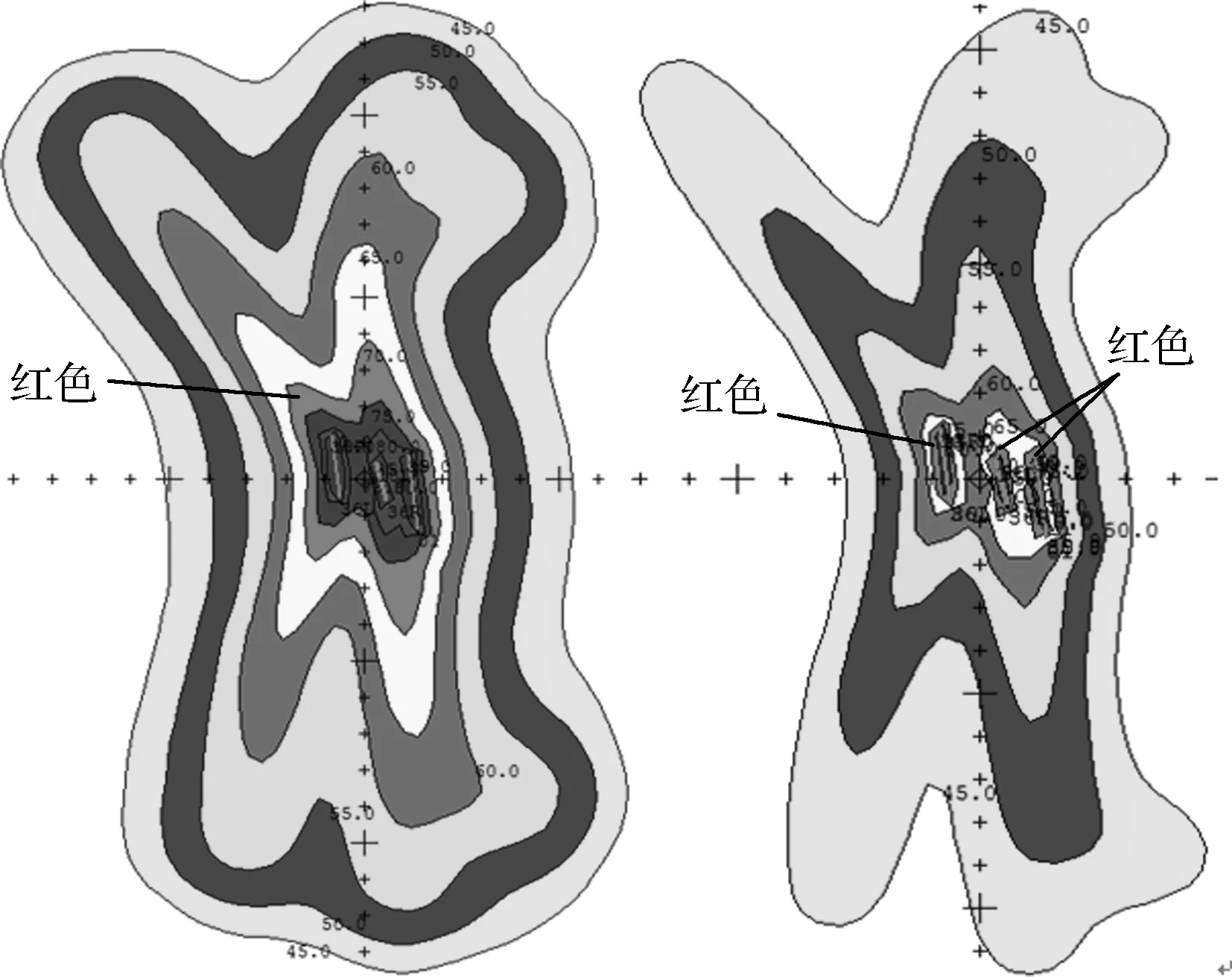
图6　飞行程序优化前后的噪声等值线对比图

图6中左图为飞行程序优化前的噪声等值线,右图为飞行程序优化后的噪声等值线图,很直观地看到飞行程序优化后其噪声等值线图总面积减小,且噪声超标面积(即红色覆盖面积)也降低。图7和图8分别为不同噪声区间内受噪声影响的人口和面积对比图。

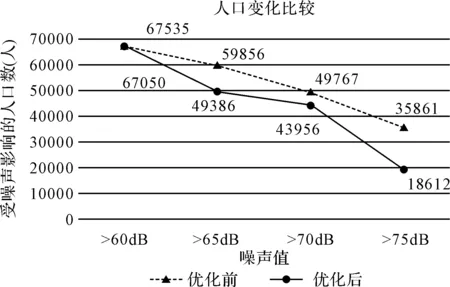
图7　飞行程序优化前后不同噪声区间内人口变化量

图8　飞行程序优化前后不同噪声区间内面积变化量

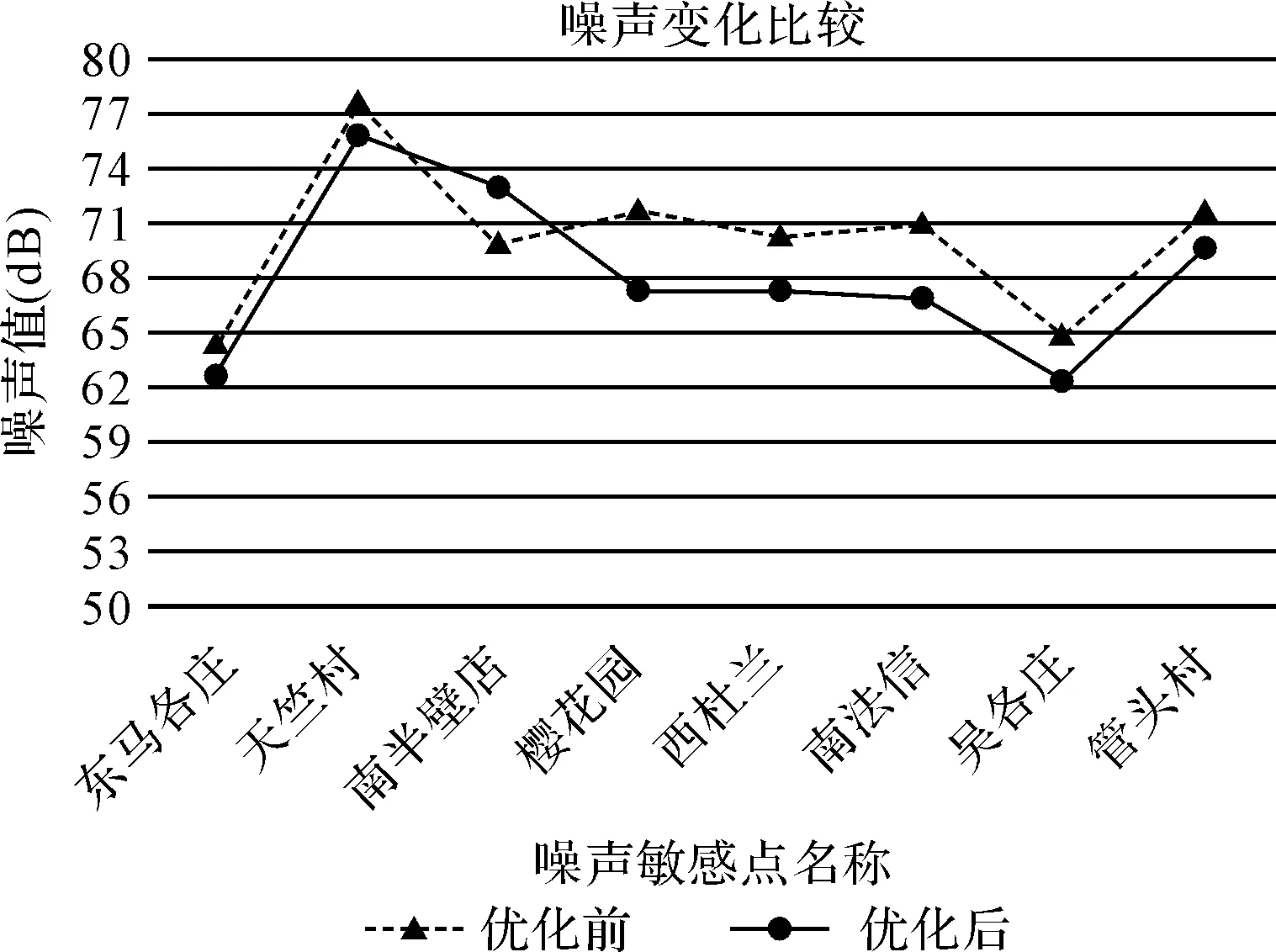
图9　飞行程序优化前后噪声敏感点的噪声值变化

从图7可以看出,不同噪声区间内的人口数量都有所降低,其中噪声大于75分贝的区域内人口数量降低了48.1%。噪声大于80分贝的区域内人口数为0,该区域在机场内,无常驻人口。图8是不同噪声区间面积的变化对比,优化后飞行程序的噪声影响面积有所降低,达到了降噪效果。

从图9中可以看出大部分噪声敏感点的噪声值得到有效降低。但南半壁店的噪声值却增大了3dB,分析原因是由于南半壁店与樱花园距离较近,而樱花园人口为17283人,约为南半壁店人口的6倍,因此为了避开人口稠密区的樱花园而以南半壁店的噪声增加为代价,总体上使得受噪声影响的总人口数降低。另外,飞行程序优化后的天竺村噪声值依然很大,原因是天竺村离36L跑道端的距离太近,飞机飞越该区域时,高度较低,难以通过飞行程序优化来减小噪声影响。

5　结语

本文对机场航迹数据进行聚类分析,将执行同一飞行程序的航迹聚为一类,并计算同一飞行程序的运行航迹的噪声影响,在此基础上定义了噪声最优航迹,研究了优化飞行程序航路点的方法,在保证飞行安全的同时降低机场周边噪声敏感点的综合噪声影响。在机场设计、土地使用等存在不足的情况下或在机场扩建的过渡时期,能够通过基于噪声最优航迹的飞行程序优化方法有效地将现行机场运行时对周边噪声敏感区域的噪声影响控制在可接受范围内,从而实现机场的环境友好性和可持续发展的要求。

[1] 国际民用航空组织.航空器噪声管理平衡做法指南[M].北京:中国民用航空局机场司,2004:16-28.

International Civil Aviation Organization. Guidelines for the Balancing Practice of Aircraft Noise Management[M]. Beijing: China Civil Aviation Administration Airport Division,2004:16-28.

[2] 闫国华,张永磊,杜海涛,等.ICAO噪声严格度对中国机队的影响[J].噪声与振动控制,2014,34(2):111-113.

YAN Guohua, ZHANG Yonglei, DU Haitao, et al. Study on the Impact of Noise Stringency of International Civil Aviation Organization(ICAO) on Chinese Fleet[J]. Noise and Vibration Control,2014,34(2):111-113.

[3] 冯霞,刘学刚.基于土地分类的机场噪声评价限值标准比较[J].环境科学与技术,2013,36(4):182-185.

FENG Xia, LIU Xuegang. Method Based on Land Use Category for Comparison of Airport-Noise-Assessment Threshold Criteria[J]. Environmental Science and Technology,2013,36(4):182-185.

[4] Prats, X., Puig, V., Quevedo, J., et al. Optimal Departure Aircraft Trajectories MinimisingPopulation Annoyance[C]//Proceedings of the 3rdInternational Congress on Research in Air Transportation(ICRAT),2008:421-428.

[5] Wijnen R. A. A, Visser H. G. Optimal Departure Trajectories with Respect to Sleep Disturbance[J]. Aerospace Science and Technology,2003,7(1):81-91.

[6] 闫国华,费代祥.大角度进近减噪探索研究[J].噪声与振动控制,2011,31(5):121-125.

YAN Guohua, FEI Daixiang. Research of Noise Reduction with Steeper Approach[J]. Noise and Vibration Control,2011,31(5):121-125.

[7] 费代祥,闫国华,鲍海滨,等.大角度进近噪声等值线绘制的探索[J].噪声与振动控制,2012,32(1):86-88.

FEI Daixiang, YAN Guohua, BAO Haibin, et al. Research of Noise Contour Plotting of Steeper Approaches[J]. Noise and Vibration Control,2012,32(1):86-88.

[8] 戴福青,李解.基于PBN的中小机场终端区飞行程序优化研究[J].科学技术与工程,2012,12(34):9270-9274.

DAI Fuqing, LI Jie. Optimization and Adjustment of Procedures for Small and Medium Airport Based on PBN[J]. Science Technology and Engineering,2012,12(34):9270-9274.

[9] 黑妍茹,胡明华.机场航空噪声及减噪声程序研究[C]//2010年航空器适航与空中交通管理学术年会论文集,2010:32-36.

HEI Yanru, HU Minghua. Studies on the Airport Aviation Noise and Noise Abatement Procedure[C]//Proceedings of the 2010 Academic Annual Conference on Aircraft and Air Traffic Management,2010:32-36.

[10] Gągorowski A. Continuous Descent Approach: Noise Testfor Warsaw International Airport[J]. Journal of KONES,2012,19(2):167-174.

[11] Guha S, Rastogi R, Shim K. CURE: an Efficient Clustering Algorithm for Large Databases[C]//ACM SIGMOD Record. ACM,1998,27(2):73-84.

[12] 徐涛,李永祥,吕宗平.基于航迹点法向距离的航迹聚类研究[J].系统工程与电子技术,2015,37(9):80-86.

XU Tao, LI Yongxiang, LV Zongping. Research on Flight Tracks Clustering Based on the Vertical Distance of Track Points[J]. Systems Engineering and Electronics,2015,37(9):80-86.

[13] Xu J L, Xu B W, Zhang W F. Stable Initialization Scheme for K-Means Clustering[J]. Wuhan University Journal of Natural Sciences,2009,14(1):24-28.

[14] 徐涛,燕宪金,杨国庆.基于神经网络集成的单个飞行事件噪声预测模型[J].中国环境科学,2014,34(2):539-544.

XU Tao, YAN Xianjin, YANG Guoqing. Prediction Model of Noise Event for Single Flight Based on Neural Network Ensemble[J]. China Environmental Science,2014,34(2):539-544.

[15] Eric R. Boeker, et al. Integrated Noise Model(INM) Version 7.0 Technical Manual[R]. Federal Aviation Administration,2008:73-76.

Flight Procedure Optimization Method Based on the Noise Optimal Flight Track
LV Zongping1CHEN Xuerui2XU Tao1,2
(1. Information Technology Research Base of Civil Aviation Administration of China, Tianjin300300)

(2. College of Computer Science and Technology, Civil Aviation University of China, Tianjin300300)

Airport’s construction promotes the economic development of the surrounding areas, and inevitably brings about the aviation noise. In order to control the aviation noise effectively, flight tracks based on different flight procedures are clustered in this paper, and then the concept of the optimal track of the noise is proposed. The noise optimal flight track is treated as a guide to optimize the flight procedures, so that the optimized flights can avoid flying over a populated area and reduce aircraft noise impact. The Beijing capital international airport is taken as an example to verify the proposed method. Once the optimized flight procedure is input into the INM(Integrated Noise Model) system, the noise value, population and area in different noise region of the noise sensitive area could be calculated and the noise contour map could be drawn. Experimental results show that the flight procedure optimization method based on the noise optimal flight track is feasible and can effectively reduce the impact of aviation noise. The proposed method has valuable theoretical reference for noise abatement procedures.

flight procedure, airport noise, flight tracks clustering, noise optimal flight track

2016年2月7日,

2016年3月15日

国家科技支撑计划课题(编号:2014BAJ04B02);中央高校基本科研业务费专项基金(编号:3122013P013)资助。

吕宗平,男,副研究员,研究方向:民航信息传输与处理等。陈雪蕊,女,硕士研究生,研究方向:数据挖掘、机器学习。徐涛,男,教授,博士生导师,研究方向:智能信息处理、智慧机场理论与方法。

TP391

10.3969/j.issn.1672-9722.2016.08.014