多方向几何非线性扩散图像去噪方法*

刘国才，王帅卿

(湖南大学 电气与信息工程学院，湖南 长沙　410082)



多方向几何非线性扩散图像去噪方法*

刘国才†，王帅卿

(湖南大学 电气与信息工程学院，湖南 长沙410082)

现有几何非线性扩散滤波器同时在水平和垂直方向进行扩散，没有考虑图像边缘的方向性，有损其去噪效果.提出根据像素8-邻域方向的梯度值检测边缘点及其边缘方向，对边缘点仅沿该边缘方向进行几何非线性扩散，而对非边缘点进行4个方向上的几何非线性扩散.5个等级噪声强度和5个典型加噪图像去噪实验结果表明，本文方法能够更有效地去除图像中的噪声，同时更好地保护图像边缘.

图像去噪；各向异性扩散滤波；非线性扩散滤波；高斯噪声；图像处理

数字图像处理技术在人们日常中的应用越来越重要，而图像去噪是图像处理工作中一直都存在的基础性问题[1-2].随着技术的发展，人们对图像去噪技术有了更高的要求，传统的方法通常是采用线性滤波，如中值滤波、均值滤波等[3].但是这些方法通常都会导致图像细节的丢失，致使图像模糊，图像边缘[4]、纹理等高频信号被滤除.许多学者通过对图像内部像素及像素块之间相关性[5-6]的深入研究，逐渐认识到图像噪声之间的无关性和图像纹理之间的相关性.出于对图像边缘纹理[7]信息的需要，具有保留边缘[8]特性的去噪方法越来越得到重视.自Perona等人[9]于1990年提出各向异性扩散滤波器(Anisotropic Diffusion Filter, ADF)以来，非线性滤波器得到了长足发展，提出了许多非线性滤波器，如全变差滤波器(Total Variation Filter, TV)[10]、双边滤波器(Bilateral Filter, BF)[11]、非局部均值滤波器(NonLocal Mean Filter, NLM)[12]等.由于各向异性扩散滤波器的扩散模型是病态的，模型解的存在性与唯一性均不能得到保证，目前已提出许多改进的ADF[13-15].最近，Wu等[16]考虑到NLM在权函数设计上的缺陷，在高斯噪声假设下考虑图像块对之间的差异概率分布，提出了按图像块差异大小概率加权的非局部均值滤波器 (Probabilistic Non-Local Means, PNLM)，提高了原NLM方法的去噪性能.

几何非线性扩散滤波器(Geometric nonlinear diffusion filter, GNLDF)是Michel-González等人[17]于2011年提出的改进ADF算法，GNLDF兼顾了图像的全局信息和局部信息.但是，GNLDF只计算水平和垂直方向的扩散系数，并据此进行扩散，而没有考虑边缘的方向性.因此，GNLDF不能很好地保护非水平和非垂直方向的边缘，而同时达到最佳的去噪效果.鉴于此，本文提出了多方向GNLDF方法.该方法根据像素8-邻域方向的梯度值检测边缘点及其边缘方向，对边缘点仅沿该边缘方向进行几何非线性扩散，而对非边缘点进行4个方向上的几何非线性扩散.因此，能够更有效地去除图像中的噪声，同时更好地保护图像边缘.

1　几何非线性扩散滤波器

GNLDF是改进的各向异性扩散滤波器.ADF模型在连续域的表达式为：

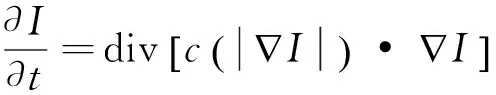
(1)

(2)

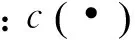
(3)

或

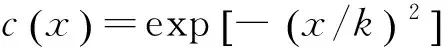
(4)

此处k的选择与图像噪声大小有关，用来控制扩散速度[12].

文献[9]中ADF的离散形式为：

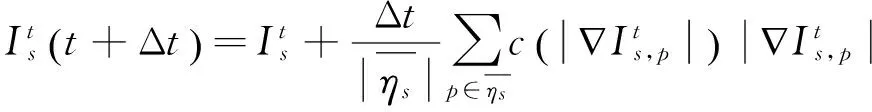
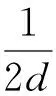
Michel-González等人[17]用像素灰度值的局部拓扑形态提出了一个新的扩散系数计算方法.以水平方向扩散系数为例，其计算方法如图1所示.图1中(a)和(b)分别是在水平方向的典型噪声像素模型和边缘像素模型；s，E和W分别为感兴趣像素点和感兴趣像素点的东边及西边的像素点.图1中：

(6)

图1　像素分类模型[17]

参数δ用MAD(Median Absolute Deviation)[13]估计，具体计算公式如下：

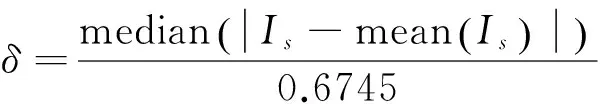
(7)

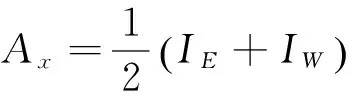
(8)

(9)

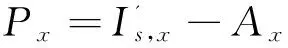
(10)

式中：Ax为x方向上的邻域像素平均值，用作给定像素点灰度值的局部参考对象.

由图1可知，在含有噪声的像素点,Px比Dx要大得多，而在边缘像素点则恰恰相反.定义相应的扩散系数如下：

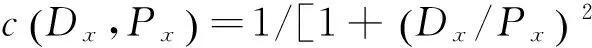
(11)

对于任何含有噪声的像素点而言，由于Px≫Dx，因此c十分接近1，因此，扩散很大.而对于边缘像素点，Px≪Dx，c十分接近0，因此，几乎不扩散.

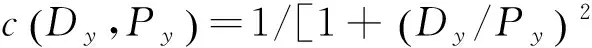
(12)

对于任何含有噪声的像素点而言，由于Py≫Dy，c十分接近1，则像素点扩散很大.而对于边缘像素点，由于Py≪Dy，c十分接近0，则像素点几乎不扩散.

与PM扩散系数由图像局部的梯度幅值和全局参数k确定相比，GNLDF的扩散系数取决于2个局部参数Dx,Px或Dy,Py，因此比原始的ADF有更好的局部扩散特性.GNLDF的离散表达式为：

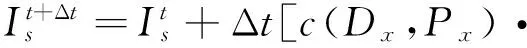
c(Dy,Py)·(N+S)]t.

(13)

GNLDF具有扩散速度快，去噪效果较好，水平和垂直方向的边缘能得到很好的保护，但对其他方向的边缘保护欠佳.

2　多方向几何非线性扩散滤波器

2.1多方向GNLDF噪声和边缘点特征

不难发现，文献[17]中提出的噪声像素点模型和边缘像素点模型是单一方向的(即水平方向或垂直方向)，因此，相应的GNLDF不能很好地保护非水平和非垂直方向的边缘而同时达到最佳的去噪效果.鉴于此，本文提出多方向GNLDF方法(MD-GNLDF)，其原理基于多方向GNLDF噪声像素点和边缘像素点特征，如图2所示，图中灰色点代表感兴趣像素点，其余部分为其八邻域像素点.

图2(a)中感兴趣的像素点(中心灰色点)受到噪声污染之后，像素的灰度值与其八邻域的像素灰度值有一定的差距.但是，依照本文中所划分的4个方向(即0°，45°，90°和135°这4个方向，下文中所指的“4个方向”均表示此含义)，其每个方向上的两个邻域像素点与感兴趣像素点的梯度幅值之和(Grad0，Grad45，Grad90和Grad135分别对应方向为0°，45°，90°和135°)大致相同.图2(b)包含一个方向为45°的边缘(本文中边的方向以45°方向为例)，图像中感兴趣像素点是一个受到噪声污染的边缘像素点(中心灰色点)，其像素的灰度值与黑色的邻域点较为接近.因此，在45°方向上的感兴趣像素点的两个邻域像素点与中心像素点的梯度幅值之和最小，而在其他3个方向上，由于白色的像素点与感兴趣像素点的梯度幅值较大，其绝对值与黑色像素点对中心像素点的梯度幅值之和相较45°方向而言较大.

图2　 噪声像素点和边缘像素点特征

具体而言，首先对计算所得Grad0，Grad45，Grad90，Grad135按照从小到大排序，取出最小值a1和第2最小值a2，用公式(14)进行计算得出R.

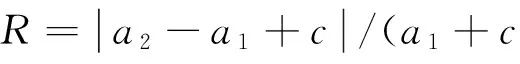
(14)

式中：c为小正数，避免分母为零.如果R很小(小于给定阈值)，即意味着a2与a1相差不大，说明此处为噪声点(也可能是平滑区域，但不管是那种情况，其本质相同)，则需要进行GNLDF扩散；反之，则说明该点可能是边缘点，需要进一步确定.如果Grad0，Grad45，Grad90和Grad135 4个中除去最小的一个，其余3个之间方差很小(小于阈值)，则可以肯定该点的确为边缘点，并且其方向为梯度幅值和最小所对应的方向(即a1值对应的方向)；反之，如果其余3个之间的方差依然很大，则依然视为噪声点.

2.2多方向GNLDF算法

基于上述多方向GNLDF噪声和边缘点特征分析，本文提出如下多方向GNLDF算法.该算法通过逐点遍历、反复迭代实现.具体过程如下：

1)把GNLDF扩展至八邻域，然后分别计算出图像I在4个方向的扩散系数c0，c45，c90和c135.

2)分别计算出图像I在4个方向上的各个梯度幅值绝对值之和Grad0，Grad45，Grad90和Grad135.

3)基于2.1节中对Grad0，Grad45，Grad90和Grad135的特征分析，判断图像中的噪声点和边缘点，并确定边缘方向.若是噪声点，则转至5)；若为边缘点，则转至4).

4)沿该边缘方向对该点进行GNLDF扩散，并转至6).

5)对该像素点同时采用扩散系数c0，c45，c90和c135进行4个方向的GNLDF扩散，并转至6).

6)若已经遍历整个图像，则转至7)；若未遍历整个图像，则转至1).

7)通过计算峰值信噪比PSNR，并与上次比较，若PSNR提高量小于DdB(缺省值为0.01 dB)，迭代终止；或者迭代次数大于N次(缺省值为500)，迭代终止.反之，跳转至1).

3　评价指标和实验结果

3.1评价指标

为了客观评价和比较本文提出的多方向GNLDF算法的有效性，采用如下客观评价指标.

1) 峰值信噪比PSNR.

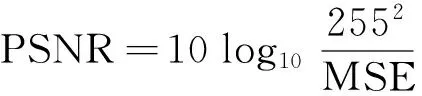
(15)

(16)

2) 结构相似度SSIM.结构相似度[18-19](Structural Similarity, SSIM)是模拟人类视觉系统提出的一种客观评价方法.设x，y为2幅待比较的图像，SSIM的模型定义为：

(17)

(18)

3) 图像增强因子IEF (Image Enhancement Factor)是评价图像平滑程度的[20]：

(19)

3.2实验结果及分析

本文中的所有实验结果均是在Matlab 2012a环境下获得的.测试的图片有Barbara，Boat，House，Pepper和Lena.图片的大小为256×256，图像的噪声类型为零均值的高斯噪声，其方差σ2所取的值分别有0.01，0.02，0.03，0.04和0.05，采用Matlab imnoise函数实现，图像的数据类型为uint8.

本文中对比的算法主要有BF[11]，NLM[12]和PNLM[16].对于BF和NLM等算法，对不同的噪声方差或不同的图像，其处理效果最好的参数并不相同，本文中的所有实验结果均是在其参数最优时的处理结果.

PNLM的参数设置为搜索区域窗口大小21×21，匹配块大小5×5，修正系数为1，并且标准差的估计采用小波MAD方法，即先对噪声图像进行小波分解，分解层数为2，采用的小波为“db8”；利用分解所得的对角方向上的细节系数矩阵用MAD方法[13]估计，这样的参数设置能够更为准确地估计出图像中噪声的方差，而直接对图像用MAD估计的方差与实际值偏差较大.

对于本文提出的多方向GNLDF算法，在整个实验过程中，参数保持不变.在高斯预滤波中，其中的高斯核参数为σ=0.53，w=9.在判断Grad0，Grad45，Grad90和Grad135之间差异时，公式(14)中R的阈值取为1，采用它们4个中最大3个的方差大小来判断，其判断阈值设置为0.001.

图3中显示的是Barbara，Boat，House，Pepper和Lena的原始图像和噪声方差为0.03的加噪图像及分别采用BF，NLM，GNLDF，PNLM以及本文提出的MD-GNLDF方法进行去噪之后的图像.通过对比，可以发现BF方法较其他3种方法的去噪效果差，NLM处理结果模糊不清，GNLDF处理结果有明显的块状效应，PNLM的结果边缘对比度下降，而本文提出的方法在视觉上更为自然.BF方法是对图像利用空间距离和灰度值相似性加权平均，是一种简单的局部滤波，效果较差.NLM是非局部滤波，但这也一定程度上造成了图像较为模糊.PNLM是针对高斯噪声在图像块对之间差异大小的概率分布，改进了原NLM.但其在强噪声环境下，边缘保留方面改进不足，细节纹理几乎消失殆尽.GNLDF主要是基于其像素点的四邻域像素点之间的关系，导致易产生块状效应.MD-GNLDF方法考虑了边缘方向，削弱了块状效应，使得图像在视觉上更为自然.

图3　原始图像、加噪图像及分别用BF，NLM，GNLDF，PNLM和本文提出的方法去噪之后的图像

通过表1对比发现，整体而言，在噪声强度较高(σ2≥0.03)的时候，本文提出的多方向GNLDF方法在PSNR，SSIM，IEF方面均有更好的表现.与原GNLDF相比，本文提出的方法，在PSNR方面，最低能够提高0.12 dB，最高能够提高0.75 dB，平均提高0.45 dB.SSIM和IEF的情况与PSNR基本类似.

但对Boat，在SSIM方面本文提出的方法和原GNLDF算法基本相当.对于Barbara，Boat，House，Lena，当σ2较小时(尤其是在σ2≤0.02)，提出的方法其PSNR要比NLM和PNLM小.出现这种情况的原因可能与图像本身的纹理复杂度有关.当噪声强度较小时，NLM和PNLM同属于非局部算法，复杂纹理图像区域有着较好的非局部性，而本文提出的方法则是基于局部的边缘点与噪声点的特征扩散滤波，因而本文的方法较NLM和PNLM差.但在强噪声(如在Pepper中，σ2=0.02时)时，MD-GNLDF去噪性能好于NLM和PNLM等.具体而言，对于Barbara图像，其人物的头巾、裤子以及桌布部分纹理变化复杂；House图像中房屋的墙壁以及屋顶纹理变化较为复杂；而Lena中则是人物的头发变化较为频繁.而这些纹理变化复杂的区域，其纹理都属于较弱的纹理，因而容易淹没在低强度的噪声当中.除此之外，对于三者图像来说，Barbara图像中这种变化复杂的区域相对较多，因而其在σ2≤0.02时MD-GNLDF去噪性能变差，而House和Lena则是在σ2=0.01时，即噪声非常小时，MD-GNLDF去噪效果才变得较差.需要说明的是，在表1中，PNLM在高噪声环境下比NLM差，之所以出现这种情况是因为PNLM的参数设置自始至终保持不变，而NLM中的实验结果是其效果最好的结果.

表1　峰值信噪比、结构相似度和图像增强因子

4　总　结

针对原GNLDF方法不能很好保护非水平方向和非垂直方向边缘的不足，本文提出的多方向GNLDF能够充分利用图像中的边缘方向信息，最大限度沿边缘方向进行GNLDF，从而能够更好地保护图像边缘，同时达到更好的去噪效果.实验证明，本文提出的改进算法在高噪声环境下能够有出色的表现，但是在低噪声环境下表现欠佳，有待进一步改善.

将本文方法推广到更多方向GNLDF(包括三维医学图像处理情况)是可能的，也是直接的.而且，在复杂边缘情况下预期可进一步提高边缘保护效果和去噪效果，有待更深入地研究.

[1]ZENG X,BIAN W,LIU W,etal.Dictionary pair learning on grassmann manifolds for image denoising[J].Image Processing,IEEE Transactions on, 2015,24(11):4556-4569.

[2]GHIMPETEANU G,BATARD T,BERTALMIO M,etal.A decomposition framework for image denoising algorithms[J].Image Processing,IEEE Transactions on,2016,25(1):388-399.

[3]李学玲,齐国清.基于方向信息测度的非线性扩散图像去噪方法[J].中国图象图形学报,2008,13(3): 400-405.

LI Xue-ling,QI Guo-qing.An image denoising method based on nonlinear diffusion and orientation information measure[J].Journal of Image and Graphics,2008,13(3):400-405.(In Chinese)

[4]单建华.改进权值函数的非局部均值去噪算法[J]. 中国图象图形学报,2012,17(10):1227-1231.

SHAN Jian-hua.Non-local means denoising algorithm with enhanced weight function[J].Journal of Image and Graphics,2012,17(10):1227-1231.(In Chinese)

[5]YUE H,SUN X,YANG J,etal.Image denoising by exploring external and internal correlations[J].Image Processing,IEEE Transactionson on,2015,24(6): 1967-1982.

[6]ZHANG X,FENG X,WANG W.Two-direction nonlocal model for image denoising[J].Image Processing,IEEE Transactionson on,2013,22(1):408-412.

[7]ZUO W,ZHANG L,SONG C,etal.Gradient histogram estimation and preservation for texture enhanced image denoising[J].Image Processing, IEEE Transactionson on,2014,23(6):2459-2472.

[8]HOSOTANI F,INUZUKA Y,HASEGAWA M,etal. Image denoising with edge-preserving and segmentation based on mask NHA[J].Image Processing,IEEE Transactionson on,2015,24(12): 6025-6033.

[9]PERONA P,MALIK J.Scale-space and edge detection using anisotropic diffusion[J].Pattern Analysis and Machine Intelligence,IEEE Transactionson on,1990,12(7):629-639.

[10]RUDIN L I,OSHER S,FATEMI E.Nonlinear total variation based noise removal algorithms[J].Physica D: Nonlinear Phenomena,1992,60(1):259-268.

[11]TOMASI C,MANDUCHI R.Bilateral filtering for gray and color images[C]//Computer Vision,Sixth International Conference.Bombay, India:IEEE,1998:839-846.

[12]BUADES A,COLL B,MOREL J M.A non-local algorithm for image denoising[C]//Computer Vision and Pattern Recognition. IEEE Computer Society Conference.San Diego,CA,USA:IEEE,2005:60-65.

[13]BLACK M J,SAPIRO G,MARIMONT D H,etal. Robust anisotropic diffusion[J].Image Processing, IEEE Transactions on,1998,7(3):421-432.

[14]BAI J,FENG X C.Fractional-order anisotropic diffusion for image denoising[J].Image Processing, IEEE Transactions on,2007,16(10):2492-2502.

[15]CHAO S M,TSAI D M.An improved anisotropic diffusion model for detail-and edge-preserving smoothing[J].Pattern Recognition Letters, 2010, 31(13):2012-2023.

[16]WU Y,TRACEY B,NATARAJAN P,etal. Probabilistic non-local means[J].Signal Processing Letters,IEEE,2013,20(8):763-766.

[17]MICHEL-GONZLEZ E, CHO M H, LEE S Y. Geometric nonlinear diffusion filter and its application to X-ray imaging[J].Biomedical Engineering Online,2011,10(1):47-63.

[18]WANG Z,BOVIK A C,SHEIKH H R,etal.Image quality assessment: from error visibility to structural similarity[J].Image Processing, IEEE Transactions on,2004,13(4):600-612.

[19]赵川,马希荣,马岭,等.一种基于各向异性扩散方程的自适应去噪方法[J].计算机科学,2014,41(11A): 133-135.

ZHAO Chuan,MA Xi-rong,MA Ling,etal.Adaptive denoising method based on anisotropic diffusion equation[J].Computer Science,2014,41(11A): 133-135.(In Chinese)

[20]VEERAKUMAR T,ESAKKIRAJAN S,VENNILA I. Edge preserving adaptive anisotropic diffusion filter approach for the suppression of impulse noise in images[J].AEU-International Journal of Electronics and Communications,2014,68(5):442-452.

Multi-directional Geometric Nonlinear Diffusion Method for Image Denoising

LIU Guo-cai†, WANG Shuai-qing

(College of Electrical and Information Engineering, Hunan Univ, Changsha, Hunan410082, China)

As the direction of edges in images is not taken into account, the original geometric nonlinear diffusion filter (GNLDF) is not in the best state for images denoising, which diffuses only in the horizontal and vertical directions. In this study, we detected the edges and their directions in images based on the magnitude of the gradient in the direction of the eight neighborhoods of each pixel, then conducted GNLDF at the edge pixel just along the directions of the edges while at any no edge pixel along all four directions. Experiment results of five typical images with five levels of noise intensity show that the proposed method can not only effectively remove the noise but also better protect the edges in images.

image denoising; anisotropic diffusion filter; nonlinear diffusion filtering; Gaussian noise；image processing

1674-2974(2016)08-0135-07

2016-01-19

国家自然科学基金资助项目(61271382，61301254，61471166)，National Natural Science Foundation of China(61271382，61301254，61471166)

刘国才(1963-)，男,湖南华容人,湖南大学教授,博士生导师†通讯联系人，E-mail:lgc630819@hnu.edu.cn

TP391.4

A