非满载液罐车侧倾稳定性模型研究*

于　迪，李显生，刘宏飞，郑雪莲，徐　艺

(吉林大学 交通学院，吉林 长春　130021)



非满载液罐车侧倾稳定性模型研究*

于迪，李显生，刘宏飞†，郑雪莲，徐艺

(吉林大学 交通学院，吉林 长春130021)

为了解决非满载液罐车在转向过程中侧倾稳定性差的问题，建立了非满载液罐车罐内液体冲击等效机械模型及整车运动学模型, 运用流固动力学耦合原理对两者进行耦合.运用此模型对5种不同尺寸比例的椭圆形截面罐体进行数值仿真试验，结果表明，当椭圆长轴(2a)与短轴(2b)之比为1.5时，液罐车所受罐内液体冲击力及力矩最小，具有较好的侧倾稳定性.研究结果为液罐车行车侧倾稳定性的研究和整车设计，提供了理论和技术支持.

液体冲击；非满载液罐车；侧倾稳定性；等效机械模型；罐体尺寸

非满载液罐车发生侧翻事故将会引起严重后果，具有影响范围大、程度深、人员伤亡严重、环境破坏剧烈的特点,因此解决非满载液罐车侧倾稳定性差的问题显得尤为重要[1].发生在高速公路上的液罐车交通事故比重较大，大多发生在转弯路段[1].研究发现，与固体货物不同，液体货物具有易变形和流动特性，罐车在非满载状态下有较大的自由流动空间，这使得罐内液体晃动成为了可能[2-3].罐内液体质心高度和侧向载荷转移量大小是影响非满载液罐车的侧倾稳定性的重要因素[4-5].

许多学者做了非满载罐车的侧倾稳定性研究.Popov等[6]为了优化椭圆形截面液罐车的尺寸参数，对基于液体质心高度的倾覆力矩进行了研究,研究表明侧覆力矩的改善有利于提高液罐车的侧倾稳定性，因此优化倾覆力矩尤为重要.Budiansky[7]在研究罐体内液体冲击时发现，液体冲击是一种由于罐体运动引起的罐内液体振动现象.液体的冲击与罐体几何尺寸、充液水平和振动频率范围等因素有关.此外，Hasheminejad等[8]研究得出结论，冲击频率和冲击力的大小也与这些因素有关，对车辆行驶状态研究的试验中发现其振动频率相对于罐内液体的冲击频率很小，因此共振现象可以忽略.

目前对于罐内液体冲击的研究方法主要有：准静态(Quasi-Static)方法[6]、流体动力学法[9]、等效机械模型法[10].准静态方法推导过程比较简单，但精度不高.流体动力学法受限于罐体内液体冲击现象的观察和解释，在理论分析上较为困难.利用等效机械模型研究液体冲击运动，将会为液罐车制动性和行驶稳定性问题的研究带来诸多便利，且精度较高，该方法将流体动力学问题转化为机械运动问题，在一定程度上弥补了流体动力学方法的不足.等效机械模型主要有弹簧-质量模型与单摆模型.弹簧-质量模型多用于描述线性横向振动模态；单摆模型的突出优点在于描述罐内液体大幅振动.

本文建立了非满载液罐车整车动力学模型和等效机械模型进行流固动力学耦合，获得非满载液罐车侧倾稳定性模型.

1　非满载液罐车侧倾稳定性模型

1.1罐内液体冲击等效机械模型

液罐车是危险化学品道路运输的重要载体，其交通事故极易造成严重的人员伤亡和环境污染.非满载液罐车罐体内的液体冲击是造成液罐车侧倾稳定性下降的主因，本文的研究对象为如图1所示的液罐车.

在液罐车罐内液体冲击的研究中，可将液体冲击运动规律用等效机械模型进行替换，等效机械模型如图2所示，对罐体进行受力分析，推导出动力学微分方程.由图2可知，n阶弹簧-质量系统，hn为罐内液体第n阶冲击质量高度.a为椭圆形长轴；b为椭圆形短轴；相对于罐体底部，h为罐内液体自由液面高，hcg为罐内液体质心高度，h1为罐内液体冲击质量高度，h0为罐内液体固定质量高度.弹簧-质量等效机械模型模拟罐内液体侧向冲击，罐内液体由冲击质量和固定质量两部分构成.等效机械模型描述罐内液体冲击原理：冲击质量受迫发生晃动，对罐体壁产生冲击力，固定质量视为罐体的一部分进行建模分析.

图1　液罐车

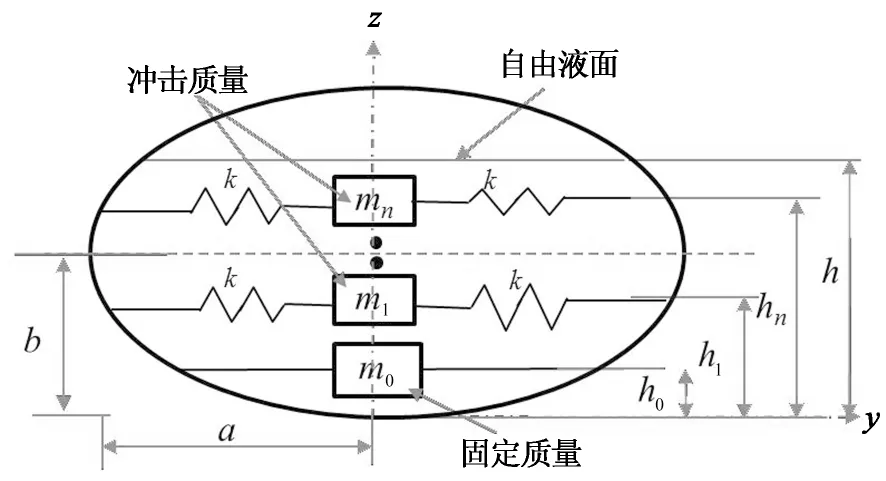
图2　罐内液体冲击等效机械模型

罐体绕定点转动时，对于n阶弹簧-质量系统，罐体受力和力矩的表达式分别为：

(1)

(2)

式中：mn为第n个冲击质量，kg；φ为外部激励函数，ysn为冲击质量位移，m；I0为固定质量转动惯量，其表达式为:

(3)

根据文献[11]，对等效模型的参数进行了精确求解，针对本文研究特点，对精确解进行了变换处理，表达式为:

(4)

令μ=(2n-1)π/2，ζ=h/2a，式(4)改写为:

(5)

式中：罐内液体质量M=ρlhc，kg；h为自由液面高度，m；l为罐体宽度，m；c为罐体长度，m；ρ为罐内液体密度，kg/m3.

(6)

(7)

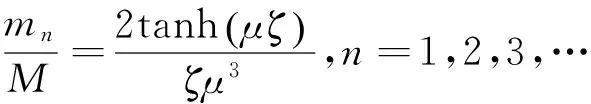
(8)

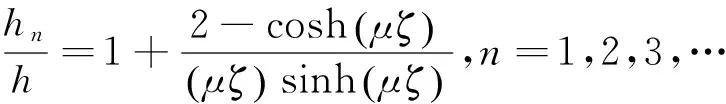
(9)

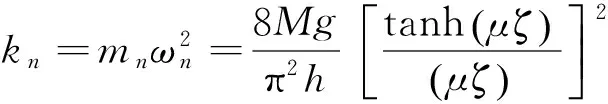
n=1,2,3,… .

(10)

式中：ωn2为第n阶液体冲击质量频率，Hz；m0和h0分别为固定质量及其位置,kg和m；mn，kn和hn分别为第n阶液体冲击质量、弹簧弹性系数及其位置，kg，N/m和m.

运用弹簧-质量系统模拟罐内液体冲击时，首先由式(5)-式(10)确定模型的相应参数，然后根据外部激励的类型及强度，可计算相应的冲击力及力矩值.

1.2非满载液罐车侧倾稳定性模型

图3为液罐车侧倾状态受力图，ms和mu分别表示簧载质量和非簧载质量，zs和φs分别表示簧载质量的垂直位移和侧倾角,zu和φu分别表示非簧载质量的垂直位移和侧倾角，ls和lt分别表示悬架位置和轮胎位置，图中其余相关参数如表1所示.液罐车整车动力学模型为:

(11)

式中：as为簧载质量加速度；au为非簧载质量加速度；αs为簧载质量侧倾角加速度；αu为非簧载质量侧倾角加速度；Fs为簧载质量所受悬架力；Fu为非簧载质量所受悬架力；Ms为簧载质量所受力矩；Mu为非簧载质量所受力矩；Mz为簧载质量所受倾覆力矩.

图3　车辆侧倾状态

参数名称参数值ms,簧载质量6500kgmu,非簧载质量3500kgmc,货物质量3500kghcs,簧载质量质心高度1.6mhca,转轴质心高度0.72mhrs,簧载质量侧倾中心高度1.1mhru,非簧载质量侧倾中心高度0.45m

(12)

式中：Fsk1和Fsk2分别为作用在簧载质量上的弹簧内外侧力；Fsc1和Fsc2分别为作用在簧载质量上内外侧阻尼力；Ftk1和Ftk2分别为作用在非簧载质量上的弹簧内外侧力；Ftc1和Ftc2分别为作用在非簧载质量上内外侧阻尼力.

2　数值仿真和实车试验

2.1非满载液罐车罐体所受冲击力及力矩仿真试验

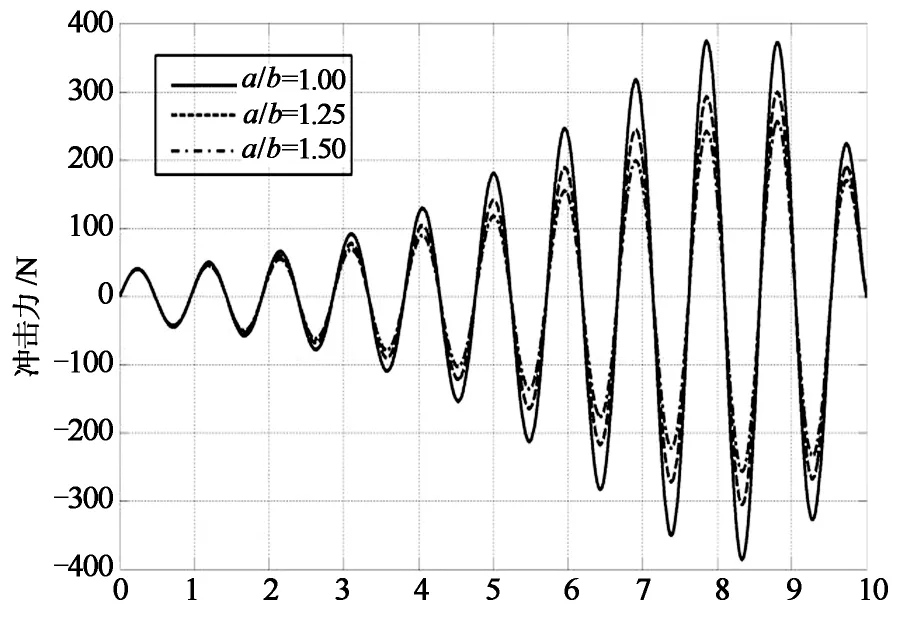
使用Matlab进行仿真实验：对5种不同比例截面尺寸的椭圆形罐体所受冲击力及力距进行比较，得出罐体所受冲击力及力矩最小的截面尺寸.仿真试验中假设罐内液体为水，密度为1 000 kg/m3；罐体总质量为4 000 kg；罐内液体充液比为80%；外部激励函数为正弦函数，车辆模型参数如表1所示.令等截面面积为6.5 m2，得到相应的仿真试验组合如表2所示，a为椭圆截面长轴，b为椭圆形截面短轴，当a/b=1.00，即为圆形截面时，运用相应的圆形截面罐内液体质心运动模型进行仿真.图4为不同尺寸比例的椭圆形罐体关于Y轴的冲击力仿真结果，图中仅表示3种比例类型.图5为不同尺寸比例椭圆形罐体的冲击力矩仿真结果，图中仅表示3种比例类型.

表2　等截面面积各罐体尺寸

由图4可知，3种罐体的曲线变化趋势是相近的，仅在数值上有所区别，当a/b=1.00时，即截面类型为圆形，所受力比其他椭圆形罐体大.由于椭圆形截面罐体相对于圆形截面具有更好的侧倾稳定性，在选择最优罐体尺寸时不考虑圆形罐体这一类型，进而单独考察4种不同截面尺寸的椭圆形，当a/b=1.25时，冲击力最大，稳定性最差，而当a/b=1.50时，所受的力最小，侧倾稳定性最优.

t/s

由图5可知，当a/b=1.00时，即截面类型为圆形，按照圆形相应的求解方程进行仿真，3种截面类型罐体所受力矩的变化趋势大致相同，但圆形截面罐体所受冲击力矩变化幅度较大，而相比之下椭圆形罐体所对应的冲击力矩则很小.通过实验数据分析可以看出，当a/b=1.25时，相对于X轴的冲击力矩是最大的，罐车侧倾稳定性较差，在设计液罐车罐体尺寸时，不建议采用此罐体尺寸比.当a/b=1.50时，冲击力矩是最小的，该尺寸液罐车具有较好的侧倾稳定性.

t/s

2.2液罐车实车试验

为了验证仿真结果的准确性，本文对市场中4种较为常见的液罐车进行了实车试验.试验液罐车规格如表3所示，可以看出，Tank3液罐车罐体外形尺寸(长×长轴×短轴=4 100 mm×1 720 mm×1 150 mm)，即长轴为1.72 m，短轴为1.15 m，与本文推荐比例a/b=1.50相近.实车试验采用单移线试验方法.

通过VBOX对液罐车罐体侧倾角和侧向加速度进行数据采集，通过数据换算得出瞬时最大力矩，统计数据如图6所示，试验表明Tank3液罐车在充液比为0.4～0.9时，侧倾力矩瞬时最大值最小，所以Tank3液罐车具有更好的侧倾稳定性，进一步证明数值仿真结论的有效性和可信度.

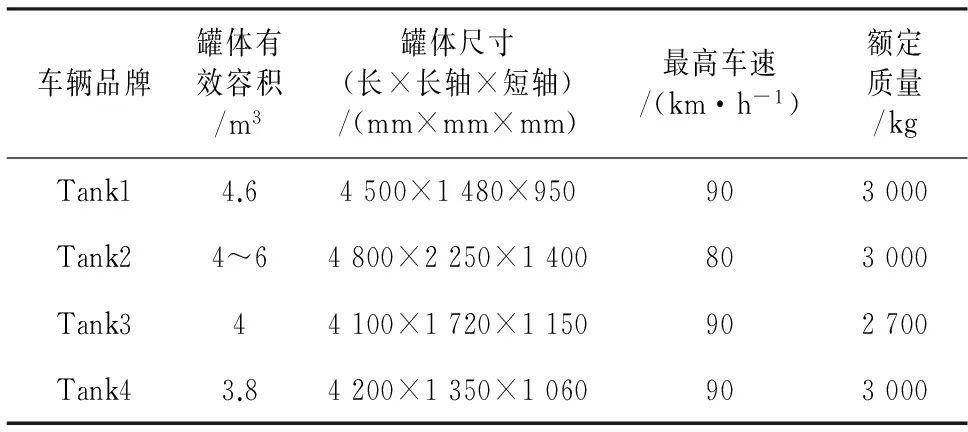
表3　试验用液罐车尺寸参数

充液比/%

3　结　论

本文建立了液罐车整车运动学模型和液体冲击等效机械模型进行流固动力学耦合，选取5种不同尺寸比例的椭圆形截面罐体进行仿真试验.结果表明，当椭圆形长轴(2a)与短轴(2b)之比为1.50时，具有较好的侧倾稳定性.通过仿真试验得出结论，罐体受到的冲击力及力矩，与罐体尺寸、充液比和自由液面长度等有关.实车试验验证了仿真结果的正确性和可信性.本文研究结果可以应用在整车设计环节，针对不同截面形状和面积，计算出侧倾稳定性最佳的罐体截面尺寸，设计出合理的罐体，从而降低研发和实车试验成本.

[1]ACARMAN T, OZGUNER U. Rollover prevention for heavy trucks using frequency shaped sliding mode control[J]. Vehicle System Dynamics, 2003, 1(10):7-12.

[2]ALIABADI S, JOHNSON A, ABEDI J. Comparison of finite element and pendulum models for simulation of sloshing[J]. Computers & Fluids, 2003, 32(4):535-545.

[3]ROMERO J A, RAMREZ O, FORTANELL J M,etal. Analysis of lateral sloshing forces within road containers with high fill levels[J]. Journal of Automobile Engineering, 2006, 220(3):303-312.

[4]KAUR A, BAKHSHI A K. Change in optimum genetic algorithm solution with changing band discontinuities and band widths of electrically conducting copolymers[J]. Chemical Physics, 2010，369:122-125.

[5]王睿,李显生,任园园,等.基于横向载荷转移量的客车侧倾稳定性分析[J].湖南大学学报:自然科学版,2013, 40(5):49-54.

WANG Rui, LI Xian-sheng, REN Yuan-yuan,etal.Roll stability analysis of passenger car based on lateral-load transfer rate[J].Journal of Hunan University：Natural Sciences,2013, 40(5): 49-54.(In Chinese)

[6]POPOV G, SANKAR S, SANKAR D T S. Shape optimization of elliptical road containers due to liquid load in steady-state turning[J]. Vehicle System Dynamics,1996,25(3):203-221.

[7]BUDIANSKY B. Sloshing of liquids in circular canals and spherical tanks[J].Journal of the Aerospace Sciences,1958, 27(3):161-173.

[8]HASHEMINEJAD S M, AGHABEIGI M. Transient sloshing in half-full horizontal elliptical tanks under lateral excitation[J].Journal of Sound and Vibration,2011, 330(14):3507-3525.

[9]KANG X,RAKHEJA S,STIHARU I.Optimal tank geometry to enhance static roll stability of partially filled tank vehicles[R].Washington DC: SAE International,1999-01-3730.

[10]郑雪莲,李显生,任园园,等.非满载罐体液体冲击等效机械模型参数确定[J].湖南大学学报:自然科学版,2013, 40(6):53-58.

ZHENG Xue-lian, LI Xian-sheng, REN Yuan-yuan,etal.Parameter values of equivalent mechanical for liquid sloshing in partially-filled tanks[J]. Journal of Hunan University:Natural Sciences,2013,40(6):53-58.(In Chinese)

[11]GRAHAM E W， RODRIGUEZ A M.Characteristics of fuel motion which affect airplane dynamics[J].Journal of Applied Mechanics, 1952,19:381-388.

Research on Roll Stability Model of Partially-filled Tankers

YU Di， LI Xian-sheng, LIU Hong-fei†, ZHENG Xue-lian, XU Yi

(College of Traffic, Jilin Univ, Changchun, Jilin130021, China)

In order to solve bad roll stability problem of partially-filled tanker in the process of steering, the liquid sloshing equivalent mechanical model and the partially filled tanker vehicle motion model were developed. Two models were coupled by dynamics of solid-fluid interaction. Five different size proportions of elliptical tankers cross section were selected to simulate, it is concluded that the tanker has better roll stability because it has minimum sloshing force and moment, when long axis (2a) and short axis (2b) of the elliptical is the ratio of 1.5. The results provide technical support for the tanker’s driving roll stability research and vehicle design.

liquid sloshing; partially-filled tank truck; roll stability; equivalent mechanical model; tank size

1674-2974(2016)08-0040-05

2015-04-15

国家自然科学基金资助项目(51375200),National Natural Science Foundation of China(51375200)；运输车辆运行安全技术交通运输行业重点实验室开放课题；吉林大学研究生创新基金资助项目(2014054)

于迪(1986-)，男，黑龙江齐齐哈尔人，吉林大学博士研究生†通讯联系人，E-mail:hongfeiliu@jlu.edu.cn

U469.5

A