具损伤压电层合微梁的坍塌特性研究*
2016-09-09陈昌萍李良中胡海涛钱长照
陈昌萍,李良中,胡海涛,钱长照 ,洪 力
(1.湖南大学 机械与运载工程学院, 湖南 长沙 410082;2.厦门理工学院 土木工程与建筑学院, 福建 厦门 361024)
具损伤压电层合微梁的坍塌特性研究*
陈昌萍1,2†,李良中1,胡海涛2,钱长照2,洪力2
(1.湖南大学 机械与运载工程学院, 湖南 长沙410082;2.厦门理工学院 土木工程与建筑学院, 福建 厦门361024)
以压电层合微梁为研究对象,基于连续介质力学理论和Euler-Bernoulli梁理论,在考虑其尺寸效应和损伤效应的情况下,推导了具损伤压电层合微梁的非线性动力控制方程.采用伽辽金法和龙格库塔法进行求解,分析了多种参数对微梁结构坍塌特性的影响.结果表明,考虑几何非线性项使得损伤微梁具有更高的坍塌阈值电压;控制电压、微梁长度等参数的变化均对损伤微梁的坍塌阈值电压造成影响.最后,采用有限元软件进行仿真模拟计算,验证了理论计算结果的合理性.本文所得结论对微机电系统压电层合微梁结构的设计具有理论指导意义.
压电效应;层合微梁;损伤效应;尺寸效应;坍塌
MEMS作为智能化和集成化的微型系统在物理、生物、机械等多个行业中广泛运用.MEMS具有多种结构形式,其中压电微结构由于压电特性在MEMS结构中具有重要地位.一种主要的压电梁式微结构形式就是将压电片通过粘结剂粘结在弹性基体而形成层合压电微梁.层合压电微梁可作为执行器和传感器两种功能结构[1],研究层合压电微梁在电场中的力学特性具有重要的意义.
近年来国内外已有许多学者对梁式微结构在电场中的静动力特性进行研究.Pamidighantam等[2]基于Euler-Bernoulli梁理论研究了两端固支和悬臂结构形式压电微梁的静、动力学特性,并得到了微梁结构的静力坍塌阈值电压.Younis和Nayfeh[3]研究了电场作用下梁式微结构谐振器的响应特性.Chaterjee和Pohit[4]分析了几何非线性对微梁结构临界坍塌电压的影响.徐琳[5]在忽略边缘效应影响的情况下分别研究了平行板式微梁结构的坍塌行为和扭转式微执行器的坍塌行为.对于压电式微梁的研究,Yin等[6]采用修正偶应力理论研究了尺度效应对压电微梁的临界坍塌电压的影响.Azizi等[7]研究了上下两侧附有压电层对微梁静动力稳定性的影响.Vahdat等[8]研究了热弹性阻尼对上下表面附有压电层微梁结构的动力学特性的影响.陈昌萍等[9]通过引入参数剥离数研究了压电粘弹性微梁的粘附特征.Xiao等[10]建立压电层合微梁的尺寸效应通用模型,并使用修正偶应力理论和汉密尔顿原理分析了层合压电微梁的坍塌现象.以上所述的研究中,研究对象大多选取理想的、无缺陷的微梁结构,而对以具损伤微梁结构为对象的研究成果很少见.本文在考虑尺寸效应的情况下,研究具损伤层合压电微梁在电场作用中的坍塌特性,并讨论几何参数、控制电压等对临界坍塌电压的影响.
1 基本方程
压电层合微梁的简化力学模型如图1所示,其中微梁的长度为L,宽度为b.微梁分为两层:上层为压电层,下层为基体层,压电层和基体层的厚度分别为hp和hb,压电层和基体层弹性模量分别为Ep和Eb.微梁整体沿长度方向的线密度为m,忽略重力对微梁的影响,固定极板与可动极板之间的真空间隙为d,真空介质的介电常数为εa,压电梁上下端加载的控制电压为Vc,固定极板与可动电极之间的电压为Vt,压电材料的压电常数为dzx.

图1 压电悬臂微梁模型
考虑几何非线性,根据Euller-Bernoulli梁理论,微梁上任意一点的轴向应变为[11]:
(1)

对于双层复合结构形式微梁,采用Reddy和Mitchell对层合结构内力的处理方法[12],得到微梁的内力分别为M(x,t)和N(x,t):
(2)

(3)
忽略电场力的边缘效应,电场力可表示为[13]:
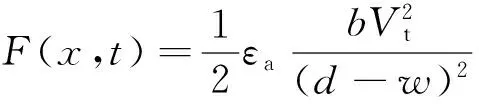
(4)
式中:w为悬臂微梁的挠度.
考虑微梁惯性力fa=-m∂2w/∂t2和阻尼力fc=c∂w/∂t作用,可得到微梁结构的非线性动力学控制方程为:
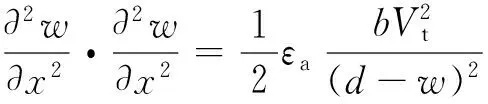
(5)
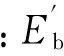
(6)
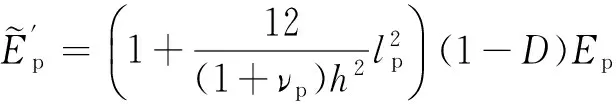
(7)
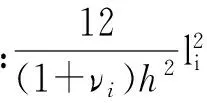
引入如下无量纲参数:
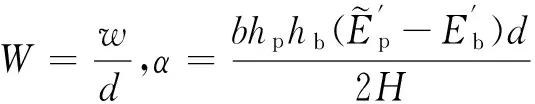
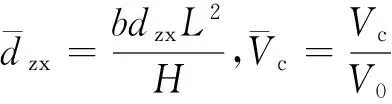
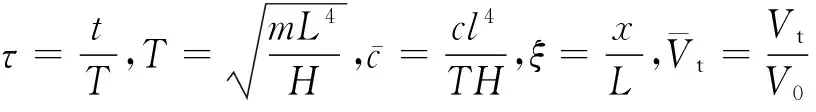
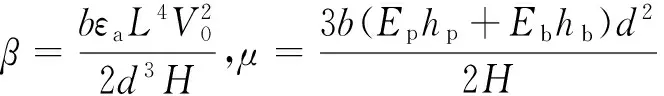
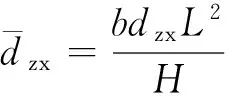
其中:
3bhphb(Eb-Ep)].
则方程(5)可以无量纲化为:
(8)
对于悬臂结构形式的压电层合微梁,其无量纲化边界条件为:
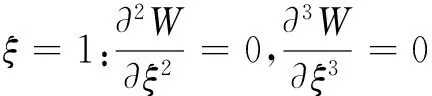
(9)
设无量纲挠度表达式为:
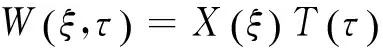
(10)

(11)
对无量纲控制方程(8)进行伽辽金积分,可得以下无量纲形式常微分动力控制方程:
α(b10+b11)[T(τ)]2-μb13[T(τ)]3=
b8[T(τ)]7}.
(12)
其中:
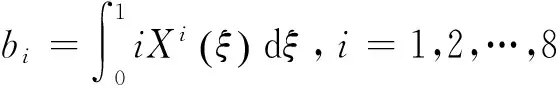
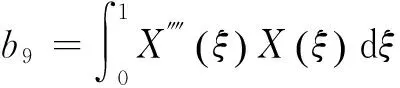
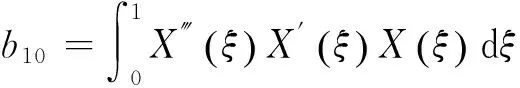

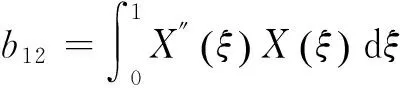

2 结果与讨论
在本文算例中,选取微梁长度L=100μm,压电层厚度hp=0.5μm,基体层厚度hb=3μm,梁宽度b=15μm,悬臂梁与固定电极初始间距d=1μm.
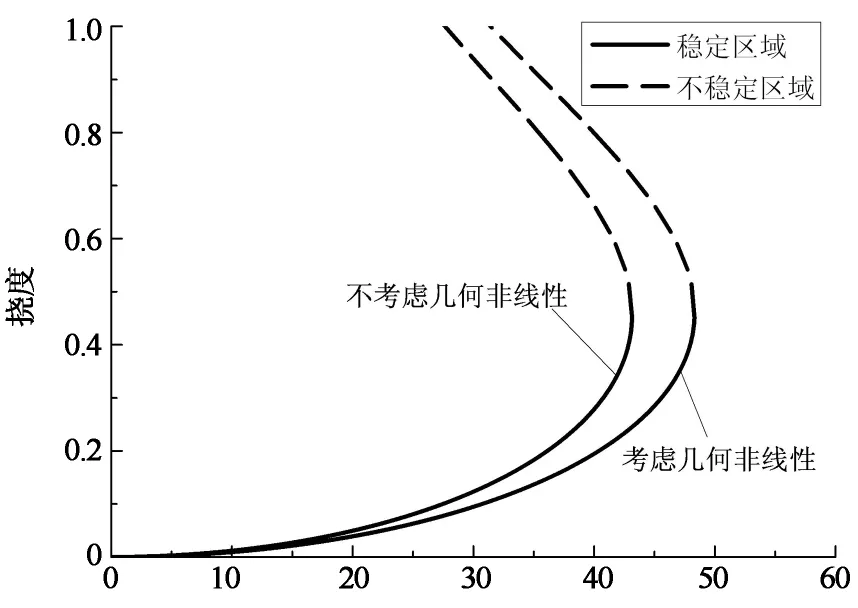
使用龙格库塔法求解无量纲常微分动力控制方程(12),得到几何非线性对微梁挠度的影响如图2所示.从图2中可知,随着负载电压的增加,微梁挠度随之增大,并当电压值超过临界坍塌电压以后,微梁的挠度变化不再稳定,并发生坍塌;几何非线性对压电微梁挠度变化趋势没有显著影响,但是可以减缓微梁的挠度变化趋势,使微梁临界坍塌电压增大.
电压
图3、图4和图5分别讨论了控制电压Vc、微梁长度L和损伤变量D对悬臂微梁挠度的影响.图3为控制电压分别取Vc=1.0,1.5,2.0V时控制电压Vc对微梁挠度的影响曲线.从图3中可以看出,随着控制电压增大,在相同负载电压下微梁的挠度会增大,而临界坍塌电压则会降低.因此,改变控制电压可以改变微梁的临界坍塌阈值电压,达到对微梁坍塌行为的控制目的.

电压

电压

电压
图4为微梁长度分别取L=90,100和110μm时,微梁长度对电压-挠度曲线的影响.从图中可以看出随着微梁长度增大,坍塌出现的负载电压会降低.
图5为损伤变量D分别取D=0,0.1和0.2时损伤变量对微梁电压-挠度曲线的影响.从图5可知,当损伤变量在一定范围内变化,且负载电压相同时,损伤程度严重,微梁挠度增大,损伤增大会导致临界坍塌电压降低.因此,坍塌临界电压随损伤变量变化的规律特性可作为微梁损伤识别的判断依据之一.
3 有限元仿真计算
为了与理论计算结果进行对比分析,本文采用有限元软件ANSYS对悬臂压电层合微梁在静电场中的坍塌行为进行计算.在有限元计算中采用与数值分析中一致的微梁参数,并采用方程(6)和(7)中的等效弹性模量来考虑微梁尺寸效应和损伤的影响.微梁的有限元模型如图6所示,在压电层与静电层的接触面添加界面,通过界面在不同的分析场中传递载荷.对悬臂梁固定端的节点进行完全约束,真空介质层约束下端z方向自由度.为了避免加载过程电压冲击对坍塌的影响,采用斜坡负载方式对微梁施加电压.在求解过程中开启网格变形控制,保证单元的变形与结构场的变形同步.图7显示了V=40V时微梁的挠度云图.微梁的右侧挠度最大,与固定极板接触的空气间隙变形小,真空介电层下端挠度为零,与理论相符合.

图6 压电悬臂微梁有限元模型
在其他条件均不变的情况下,记录不同负载电压下微梁自由端的挠度值可得出层合压电微梁的挠度与电压关系的曲线如图8所示.由图8可知,随着负载电压的增大,微梁的挠度同样增大,当负载电压接近坍塌临界电压时,微梁挠度会迅速增加使微梁与电极贴合.仿真结果与数值计算结果一致.

图7 V=40 V时压电微梁挠度云图

电压
微梁长度和损伤变量对微梁挠度和临界坍塌电压的影响分析结果分别如图9和图10所示.当长度增加时微梁挠度变大,临界坍塌电压变小,损伤变量增大时微梁挠度也变大.仿真结果和数值分析结果一致.

电压

电压
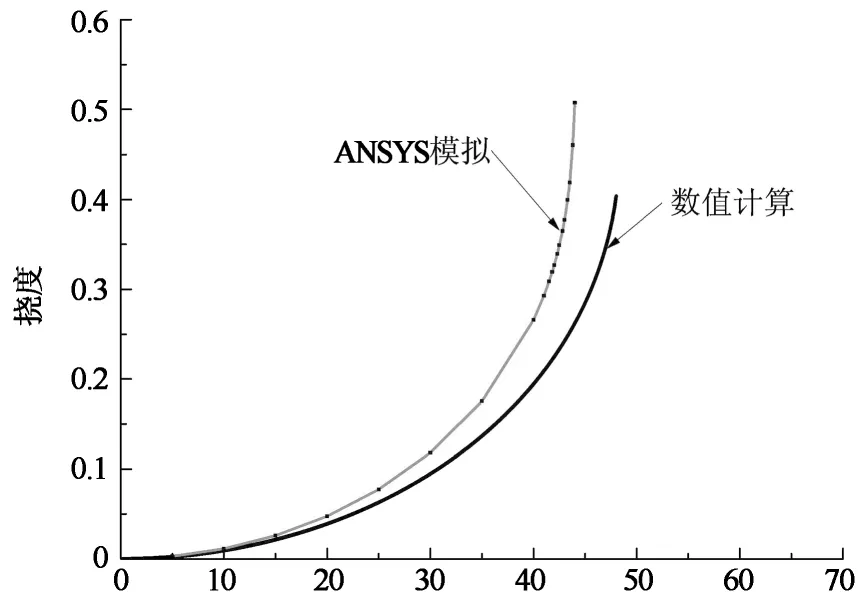
数值计算和有限元分析2种方法获得的临界坍塌电压结果如图11所示,并在表1中将具体数据进行比较.从图11和表1中可以看出,在相同电压条件下ANSYS进行有限元计算得出的临界坍塌电压较低,与使用荣格库塔法得出的临界坍塌电压相差7.8%,表明了计算结果的合理性.
电压

临界坍塌电压数值计算结果有限元计算结果相对误差/%48.044.37.8
4 结 论
本文通过数值计算和有限元仿真两种方法对具损伤的悬臂压电微梁在电场作用下非线性坍塌行为进行研究,讨论了几何非线性、控制电压等参数对微梁坍塌行为的影响.研究结果表明,考虑几何非线性使微梁具有更高的坍塌阈值电压;控制电压和微梁长度增大可导致微梁坍塌阈值电压明显降低.材料损伤变量在一定范围内增大会使微梁挠度和临界坍塌电压发生降低.因此,压电微梁结构在使用过程中产生轻微损伤,可以通过改变控制电压使其继续满足工作要求,从而延长压电微梁结构的使用寿命.
[1]YI X, DUAN H L. Surface stress induced by interactions of adsorbates and its effect on deformation and frequency of microcantilever sensors [J]. Journal of the Mechanics and Physics of Solids, 2009, 57( 8): 1254-1266.
[2]PAMIDIGHANTAM S, PUERS R, BAERT K,etal. Pull-in coltage analysis of electrostatically actuated beam structures with fixed-fixed and fixed-free conditions[J].Journal of Micromechanics and Microengineering,2002,12(4):456-468.
[3]YOUNIS M I, NAYFEH A H. A study of the nonlinear response of a resonant microbeam to an electric actuation[J]. Nonlinear Dynamics,2003,31(1):91-117.
[4]CHATERJEE S P, POHIT G.A large deflection model for the Pull-in analysis of electrostatically actuated micro-cantilever beams[J].Journal of Sound and Vibration,2009, 322(4/5): 969-986.
[5]徐琳. 静电微执行器的Pull-in特性分析[D].南京:南京邮电大学光电工程学院,2012.
XU Lin.Pull-in characteristic analysis of electrostatic micro-actuators[D].Nanjing:School of Optoelectronic Engineering,Nanjing University of Posts and Telecommunications,2012.(In Chinese)
[6]YIN L, QIAN Q, WANG Y S,etal. Size effect on the static behavior of electrostaticlly actuated microbeams [J]. Acta Mechanics Sinica,2011,27(3):445-451.
[7]AZIZI S, REZAZADEH G, GHAZAVI M-R,etal. Stabiliz- ing the Pull-in instability of an electro-statically actuated microbeam using piezoelectric actuation[J].Applied Mathematical Modelling,2011,35(10):4796-4815.
[8]VAHDAT A S, REZAZADEH G, AHMADI G. Thermoelastic damping in a micro-beam resonator tunable with piezoelectric layers[J].Acta Mechanica Solida Sinica,2012, 25(1): 73-81.
[9]陈昌萍, 李受坚. 压电粘弹性微梁的粘附分析[J].湖南大学学报:自然科学版,2013,40(11):58-63.
CHEN Chang-ping,LI Shou-jian.Adhesion analysis of a piezoelectric viscoelastic microbeam[J].Journal of Hunan University:Natural Sciences,2013,40(11):58-63. (In Chinese)
[10]XIAO Y, WANG B L, ZHOU S J. Pull-in voltage analysis of electrostatically actuated MEMS with piezoelectric layers: a size-dependent model[J].Mechanics Research Communications,2015,66(4):7-14.
[11]DYM C L, SHAMES I H. Solid mechanics: a variational approach[M].Beijing: China Railway Publishing House, 1984:88-105.
[12]MITCHELL J A, REDDY J N. A refined hybrid plate theory for composite laminates with piezoelectric laminae [J]. International Journal of Solids and Structures,1995,32(16):2345-2367.
[13]NAYFEH A H, YOUNIS M I. A study of nonlinear response of a resonant microbeam to an electric actuation [J]. Nonlinear Dynamics, 2003, 31: 91-117.
[14]DRAGON A,MROZ Z.A continuum model for plastic-brittle behaviour of rock and concrete[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts,1979,17:121-137.
[15]李兆霞. 损伤力学及其运用[M].北京:科学出版社, 2002:16-24.
LI Zhao-xia.Damage mechanics and applications[M]. Beijing: Science Press,2002:16-24.(In Chinese)
[16]李良中.具损伤微纳米结构的非线性动力学分析[D].长沙:湖南大学机械与运载工程学院,2014.
LI Liang-zhong.Nonlinear dynamic analysis of micro-structure with damage[D].Changsha:College of Mechanical and Vehicle Engineering,Hunan University,2014.(In Chinese)
Study on the Pull-in Characteristics of PiezoelectricLaminated Micro-beam with Damage
CHEN Chang-ping1,2†, LI Liang-zhong1, HU Hai-tao2, QIAN Chang-zhao2, HONG Li2
(1.College of Mechanical and Vehicle Engineering,Hunan Univ,Changsha,Hunan410082,China;2.School of Civil Engineering and Architecture, Xiamen Univ of Technology, Xiamen, Fujian361024, China)
The nonlinear pull-in behavior of piezoelectric laminated micro-beam was studied with consideration of the size effect and damage effect. Based on the theories of continuum mechanics and Euler-Bernoulli beam hypothesis, the nonlinear governing equation of piezoelectric laminated micro-beam with damage was established and solved in Galerkin method and Runge-Kutta method. The influence of various parameters on the pull-in voltage of the micro-beam was discussed, and the results have shown that the geometry nonlinearity can improve the value of critical pull-in voltage of the micro-beam; the changes of governing voltage, micro-beam length and other parameters have influences on the critical pull-in voltage of the micro-beam. Besides,the FEM software was used to carry out the check-up calculations, and the results were compared with the theoretical results. The findings of this research can offer guidance to the design of micro-structures.
miezoelectric effect; laminated micro-beam; damage effect; size effect; pull-in
1674-2974(2016)08-0057-06
2015-09-02
国家自然科学基金资助项目(11272270), National Natural Science Foundation of China(11272270)
陈昌萍(1971-),男, 江西萍乡人,厦门理工学院教授,博士†通讯联系人,E-mail:cpchen@126.com
O345
A
