基于坐标变换的微网功率解耦及限幅控制策略*
2016-09-09颜湘武王月茹王星海
颜湘武,王月茹,王星海
(华北电力大学 电气与电子工程学院,河北 保定 071003)
基于坐标变换的微网功率解耦及限幅控制策略*
颜湘武,王月茹†,王星海
(华北电力大学 电气与电子工程学院,河北 保定071003)
传统的功率下垂控制在低压微电网中的直接应用会引起有功和无功功率的耦合问题,为此采用了基于坐标变换的虚拟功率下垂控制方法,并对其解耦特性、功率均分及限幅问题进行了研究.利用相对增益分析方法分析了采用坐标变换后系统功率的耦合程度,从理论上证明了当坐标变换矩阵与线路阻抗的阻感比相同时,虚拟功率下垂控制可以实现功率的完全解耦.针对线路阻抗差异而导致的功率无法均分问题,提出了通过增加虚拟负阻抗来实现并联逆变器间功率均分的方法.考虑到现有的虚拟功率下垂限幅范围与实际功率限幅范围的不对等性,提出了新型虚拟功率下垂限幅控制方法,将功率越限部分划分为8个区域,根据逆变器输出的实际功率确定其所属区域,进而采取相应的限幅调整措施.仿真结果验证了所提控制策略的正确性和有效性.
微电网;功率控制;坐标变换;虚拟功率;解耦;虚拟阻抗;功率限幅
近年来,包含不同能源形式的微电网系统成为了国内外研究的热点,其存在2种典型的运行模式:正常情况下的联网模式与电网故障情况下的孤岛模式[1].如何实现低压微电网线路阻性成分较大情况下的有功、无功功率解耦控制以及并联分布式电源(Distributed Generation, DG)的功率均分是微电网孤岛运行模式下需要解决的重要问题.
下垂控制凭借其只需电源自身信息、不需互连线、更利于实现即插即用的优势,成为了多逆变器并联时应用最多的控制策略[2].但传统的下垂控制是基于高压输电系统线路呈感性这一条件的,而微电网中线路的阻性成分往往不可忽略,下垂控制在微电网中的直接应用必然产生有功、无功功率的耦合问题,这对微网的稳定运行、微源间有功无功出力的分配等将产生很大影响[3].文献[4]提出了通过对控制器参数进行设计使逆变器输出阻抗呈感性的方法,但控制器参数调节范围有限,其调节的前提是不影响系统的动态与稳态性能.文献[5]提出了基于线路阻抗参数进行坐标变换的虚拟功率下垂控制,该方法解决了线路阻抗所造成的功率耦合问题,但存在线路阻抗不同时有功、无功功率无法均分的问题.针对虚拟功率下垂控制存在的问题,虚拟电压-频率控制[6-7]被提出,但该方法不合乎频率与电压的电能质量评价体系,难以在实际工程中应用[8].文献[9]采用了虚拟电抗的方式以增大逆变器出口到并联点之间的等效电抗,进而实现了有功和无功功率的解耦控制,但过大的虚拟电抗会影响公共耦合点(Point of Common Coupling, PCC)的电压质量[10].文献[11]提出了P-V和Q-f下垂控制,但该方法不适用于线路阻性和感性成分均不可忽略的微电网,且存在与传统同步发电机控制不兼容的问题.
本文以2台同容量的孤岛运行的并联逆变器为研究对象,采用了基于坐标变换的虚拟功率下垂控制方法,利用文献[3]的相对增益分析方法对采用坐标变换后功率的耦合程度进行了分析,针对并联逆变器线路阻抗不同的情况,提出了通过增加虚拟负阻抗来实现功率均分的控制策略.此外,提出了逆变器的新型虚拟功率限幅控制方法,通过对逆变器的运行范围进行区域划分,根据逆变器的实时运行状态确定其所属区域及是否发生功率越限,并作出相应的调整措施,确保逆变器的输出功率在其允许的范围之内.
1 基于坐标变换的虚拟功率下垂控制
1.1虚拟功率下垂控制策略
逆变器一般等效为有内阻的电压源,由于本文采用了跟踪性能较好的准比例谐振控制器实现对逆变器电压环的控制,通过合适的参数设置,可以基本实现稳态零误差调节[9],故逆变器的输出阻抗忽略不计,从而可以简化为理想电压源.
图1为简化的单台逆变器通过线路向PCC传送能量的示意图.其中,E和V分别表示逆变器的输出电压和PCC电压的有效值,δ为两电压的角度差,即功角差,Z=R+jX表示线路阻抗,P和Q分别为有功和无功功率.
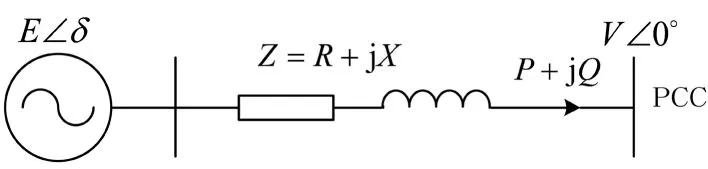
图1 单台逆变器的潮流传输示意图
根据潮流传输关系,可得:

(1)
通常可以对上述方程做近似处理:sinδ≈δ,cosδ≈1.传统的高压输电线路电阻较小,可以近似忽略.在上述2个条件成立的前提下,可得:
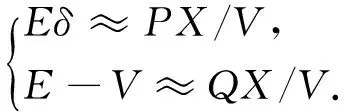
(2)
通过式(2)可以近似得到有功功率与功角差有关,无功功率与电压幅值差有关的结论,而功角差可以通过频率进行调节,因此传统下垂控制采用P-ω,Q-U的调节方式.
由以上分析可知,传统下垂控制适用于线路阻抗呈感性的情况下,但低压微电网线路的阻性成分往往较大,不可忽略,线路一般呈阻感性,不再存在有功与频率、无功与电压之间一一对应的关系,因此在低压微电网中采用传统下垂控制必然造成有功、无功功率的耦合问题.
考虑线路阻抗时,可以对式(1)进行如下处理:
(3)
令P′=PX/Z-QR/Z,Q′=PR/Z+QX/Z,再考虑近似条件sinδ≈δ,cosδ≈1,代入式(3),得
(4)
(5)
经过坐标变换得到的虚拟有功P′与功角差δ,虚拟无功Q′与电压差E-V有近似的一一对应关系,实现了功率的解耦控制,因此可以采用P′-ω,Q′-U的控制方式,下垂控制方程式为:
(6)

1.2功率耦合程度分析
为了进一步分析上述控制策略的解耦效果,采用文献[3]的相对增益分析方法,假设逆变器输出端连接线路的阻抗为Z=R+jX,变换矩阵的阻抗参数为Zt=Rt+jXt,由式(1)及功角差δ的近似条件可得逆变器的输出功率表达式为:
(7)
将式(7)代入式(5),得
(8)
结合式(8)与文献[3]中相关内容,可得衡量坐标变换后的虚拟功率与功角差、电压差之间的耦合程度的相对增益阵列如表1所示.

表1 相对增益阵列表
表1中,相对增益矩阵的每一行、每一列元素之和均为1,主对角线元素为:
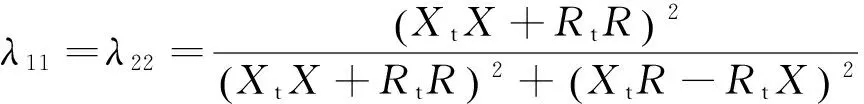
(9)
主对角线元素越接近1,则表示控制作用越强,而耦合作用越弱[3].采用阻感比的形式代替式(9)中的电阻与感抗值,定义k=R/X,kt=Rt/Xt,则式(9)可简化为:
(10)
为了更直观地表示相对增益的大小,图2给出了线路阻抗的阻感比固定时,相对增益矩阵主对角线元素的大小随着变换矩阵阻感比变化的曲线,其中变换矩阵阻感比kt的取值范围为0.1~10,线路阻抗选取了阻感比k=1与k=2两种情况.
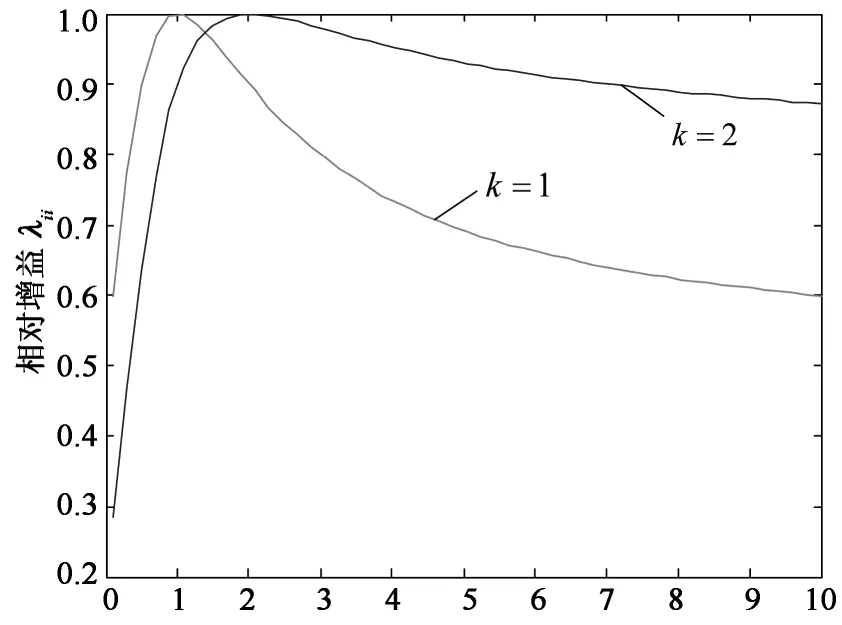
变换矩阵阻感比kt
由图2可知,当kt=k,即选取的变换矩阵的阻感比与线路阻抗的阻感比相等时,λii=1成立,此时不存在耦合作用;对于某一确定的线路阻感比k,当变换矩阵的阻感比kt与其相差越大时,λii的值越小,系统的耦合越严重.
虚拟功率下垂控制对逆变器的输出功率进行了坐标变换,如果并联逆变器选取的变换矩阵阻感比不同,则相当于将逆变器的输出功率变换到了不同的坐标系下,导致频率、电压无法起到实际功率分配的通信媒介的作用,在没有通信连接的并联逆变器控制中,较为简单的一种方法是所有并联逆变器选取相同的变换矩阵,则可以通过控制虚拟功率实现比例分配来达到实际功率合理分配的目的.
结合以上分析可知,当所有并联逆变器所接的线路型号相同时,即线路阻抗的阻感比相同,此时可以选取相同的变换矩阵,该矩阵参数由相应的线路阻抗参数确定,该情况下所有逆变器的虚拟有功与频率、虚拟无功与电压之间都是解耦的,且功率控制较为简单.当微网中的线路类型不只有一种时,采用相同的变换矩阵必然会存在部分逆变器无法完全解耦的问题,但由于篇幅有限,本文仅考虑微网中线路型号相同的情况.
1.3控制策略的不足及相应的改进措施
由1.2节分析可知,当所有并联逆变器所接的线路具有相同的阻感比时,采用虚拟功率下垂控制可以实现逆变器的解耦控制,加快并联系统的动态响应速度,提高系统的稳定性.上述方法虽然实现了解耦的目的,但并联逆变器的功率分配问题仍需考虑,文献[2]指出并联逆变器可以按照容量比例分配负荷功率的条件是等效输出阻抗与容量成反比,由于1.1节指出本文不考虑逆变器的输出阻抗,故文献[2]的等效输出阻抗即为本文的线路阻抗,易知当线路阻抗不满足与逆变器容量成反比时,虚拟无功功率无法实现比例分配.本文以相同容量的逆变器并联为例,当线路阻抗不相同时,虚拟无功功率无法均分,文献[12]指出由于变换矩阵是非奇异的,虚拟无功功率的不均分将导致有功和无功功率都无法均分,因而采用虚拟功率下垂控制后的均流效果比传统下垂控制更差.
线路阻抗不同是导致并联逆变器输出功率无法均分的直接原因,在已知线路阻抗的前提下,可以通过虚拟阻抗技术减小并联线路阻抗的差异,进而提高功率分配精度.图3给出了虚拟阻抗法的原理图.
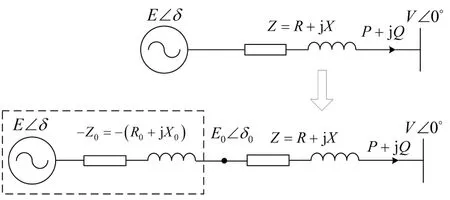
图3 虚拟阻抗法原理图
图3中,在线路阻抗为Z的逆变器控制中加入了数值大小为Z0=R0+jX0的虚拟负阻抗,逆变器的等效线路阻抗变为Z-Z0,只需通过控制Z0的大小使得该逆变器的等效线路阻抗与其并联逆变器的相等即可实现功率的均分.同时,由于加入的是虚拟负阻抗,不会带来PCC电压跌落的问题.
虚拟负阻抗技术的实现可以通过采集线路电流,计算出电压降落,再由下垂环节得到的参考电压加上计算所得的电压降落即可.为了避免对电流进行求导,采用了文献[9]中提出的在αβ坐标系下实现虚拟阻抗的方法.设三相电流在αβ坐标系下的分量分别为Iα和Iβ,则Z0上的电压降落为:
(11)
因此,只需要将参考电压变换到αβ坐标系下,然后加上计算得到的电压降落,即可实现虚拟负阻抗环节.
2 虚拟功率下垂限幅控制
孤岛运行的逆变器直流侧一般接有储能装置,单台逆变器的输送功率必须保持在一定范围内,才能保证系统的安全.负荷突增时,可能超过逆变器的最大容量而损坏逆变器,或者导致直流侧储能装置过度放电而受损;当负荷突减时,逆变器的功率可以双向流动,可能导致直流侧储能装置过充电[13],因此必须对逆变器的功率运行范围加以限制.
假设逆变器的安全运行范围为0≤P≤Pmax,-Qmax≤Q≤Qmax,即为图4中的阴影部分.其中,θ满足cosθ=Rt/Zt.
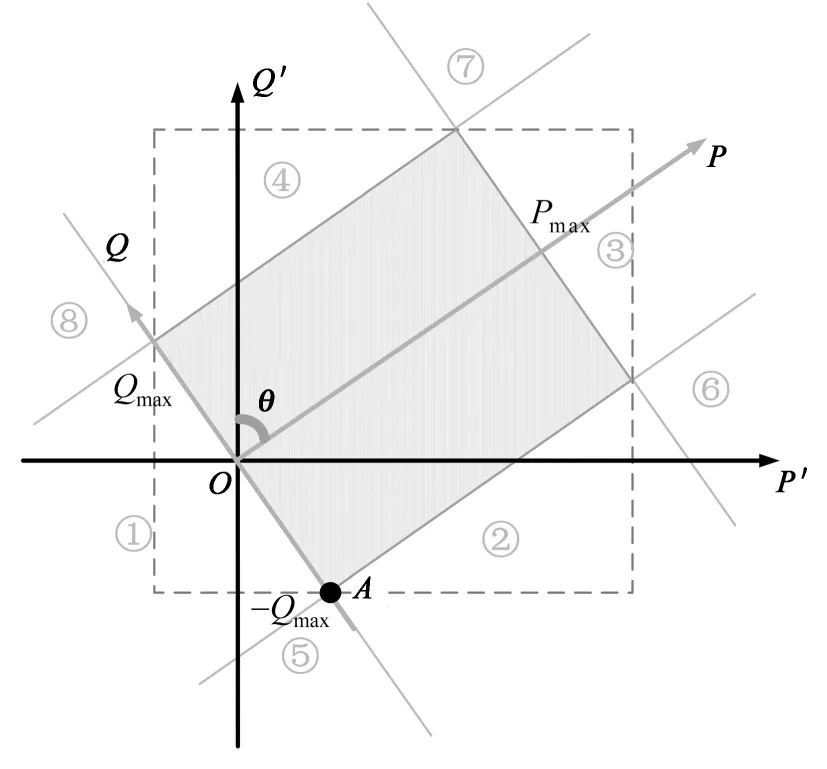
图4 坐标变换示意图
经过坐标变换后,需要得到P′-Q′坐标系下的运行范围使其与P-Q坐标系下的范围一致,文献[8]给出的P′-Q′坐标系下的运行范围为:
(12)
式(12)所对应的为图4中虚线所围成的矩形区域,显然此运行范围还包含了阴影部分之外的区域,因此按照这一范围对逆变器输出的虚拟功率进行限幅控制,可能会导致虚拟功率在限幅范围内,但实际功率已超出其规定的运行范围,因此文献[8]提出的虚拟功率限幅范围并不合理.
虚拟功率下垂限幅控制实现的难点在于操作变量ω和E与P′和Q′之间近似呈一一对应关系,但与实际的P和Q之间无直接对应关系,因此需要确定P′和Q′的运行范围,通过P′和Q′的大小确定是否发生了功率越限,如果发生了功率越限,再采取相应的调节措施.
本文提出了一种新型虚拟功率下垂限幅控制方法,通过对下垂控制方程式中的Δω和ΔE的调节来实现限幅控制.
(13)
本文提出的下垂限幅控制通过P和Q直接确定是否发生功率越限以及越限发生后的相应调节措施.如图4所示,将阴影区域外侧分为8个区域:①-⑧ ,根据区域编号的不同,采取不同的限幅调节措施.以区域①为例,其范围为P<0,-Qmax 表2中仅给出了功率越限后的判断依据及调节方式,功率未发生越限时的判断依据为0≤P≤Pmax,-Qmax≤Q≤Qmax;此时,Δω和ΔE均应保持不变. 式(13)中,通过调节Δω和ΔE来实现限幅控制.定义2个变量flag_ω与flag_E用以确定Δω和ΔE的调节方向,2个变量的取值各有3种情况:-1,0和1.另外定义step_ω与step_E用以表示Δω和ΔE调整步长的大小.以Δω的调节为例,具体方法为:根据P和Q的大小,确定运行点所属区域,进而判断得出Δω的调节方向,若Δω↑,则flag_ω=1;若Δω→,则flag_ω=0;若Δω↓,则flag_ω=-1.式(14)即为Δω的确定方式. Δωk=Δωk-1+flag_ω×step_ω. (14) 式中:Δωk和Δωk-1分别为本次与上一次ω的限幅调节量.ΔE的调节方法与Δω相同,这里不再给出. 表2 功率限幅范围及调节方法 注:↑表示增加;→表示不变;↓表示减小. 本文以2台额定容量均为10 kW和4 kVar的孤岛运行的逆变器并联为例在Matlab中搭建了仿真系统,系统额定相电压为220 V,两逆变器通过线路接至PCC共同为负荷供电.并联系统的简化模型如图5所示. 图5 并联系统简化模型 图5中,Z1和Z2均为线路阻抗,本文选取的线路阻抗阻感比为1,具体数值为:Z1=(0.7+j0.7)Ω,Z2=(0.5+j0.5)Ω. 图6和图7分别给出了传统下垂控制与虚拟功率下垂控制的仿真结果.图6的仿真时间为0.4 s,并联系统共同承担20 kW和8 kVar负荷.图7的仿真时间为1.2 s,0.4 s之前仿真条件与图6相同,0.4 s后在DG1的控制中加入了Z0=(0.2+j0.2)Ω的虚拟负阻抗,为了观察控制策略的动态性能,在0.8 s时并联系统突增有功和无功功率的负荷分别为3 kW和2 kVar. t/s t/s t/s t/s t/s t/s 由图6可知,由于线路阻性成分不能忽略,传统下垂控制输出功率出现振荡,系统无法稳定运行.由图7可知,采用虚拟功率下垂控制方法后,并联系统可以稳定运行,达到了解耦的目的.当时间为0~0.4s时,由于线路阻抗不一致,图7(d)中逆变器的虚拟无功功率不均分,则图7(a)和(b)中逆变器输出的有功、无功功率都各不相等;当时间为0.4~0.8s时,增加虚拟负阻抗后,图7(d)中逆变器的虚拟无功可以实现均分,则图7(a)和(b)中的实际功率均分效果也较为理想;当时间为0.8s后,负荷突增,经过短暂的过渡过程后,系统重新进入稳态,且具有良好的动态功率均分效果.仿真结果表明,本文所提出的加入虚拟负阻抗的虚拟功率下垂控制实现了解耦的目的,提高了并联系统的稳定性,且具有良好的稳态与动态功率均分性能. 为了验证功率限幅控制方法的有效性,仍采取图7仿真条件中两逆变器线路阻抗与虚拟负阻抗的大小,设置并联系统的负荷有功和无功分别为30 kW和8 kVar,逆变器的最大输出有功和无功功率分别为Pmax=12 kW和Qmax=6kVar.0.4s前采用的是文献[8]的限幅范围,0.4s后切换为本文所提出的限幅控制方法.图8给出了仿真结果. t/s t/s t/s t/s 根据式(12)可以得到文献[8]的虚拟有功和无功功率运行范围分别为-4.24kW≤P′≤12.73kW和-4.24kVar≤Q′≤12.73kVar.0.4 s前采用的是文献[8]的限幅范围,由图8(c)和(d)可以看出,逆变器的虚拟有功和虚拟无功功率均在合理范围内,但由图8(a)可知,实际的有功功率已经越限,则验证了文献[8]的虚拟功率限幅范围是不合理的.0.4 s后切换为本文所提出的限幅控制方法,经过调节后,实际的有功和无功功率都保持在允许的范围之内,则验证了本文所提限幅控制方法的正确性. 针对低压微电网线路普遍呈阻感性而引起的功率耦合问题,采用了基于坐标变换的虚拟功率下垂控制方法,利用相对增益分析方法分析了变换矩阵的选取与解耦程度的关系,得出了当变换矩阵的阻感比与线路阻抗阻感比相同时可以实现完全解耦的结论.针对线路阻抗不等时虚拟功率下垂控制方法无法保证功率均分的问题,提出了增加虚拟负阻抗以减小线路阻抗差异的方法,达到了并联微源间功率均分的目的.此外,提出了针对虚拟功率下垂控制输出功率的新型限幅方法,确保各台并联逆变器准确运行在安全工作范围内. [1]王成山,肖朝霞,王守相.微网综合控制与分析[J].电力系统自动化,2008,32(7):98-103. WANG Cheng-shan,XIAO Zhao-xia,WANG Shou-xiang.Synthetical control and analysis of microgrid[J].Automation of Electric Power Systems,2008,32(7):98-103.(In Chinese) [2]吕志鹏,罗安.不同容量微源逆变器并联功率鲁棒控制[J].中国电机工程学报,2012,32(12):35-42. LV Zhi-peng,LUO An.Robust power control of paralleled micro-source inverters with different power ratings[J].Proceedings of the CSEE, 2012,32(12):35-42. (In Chinese) [3]李鹏,杨世旺,王阳,等.基于相对增益分析的目标函数对角化微网功率解耦控制方法[J].中国电机工程学报,2014,34(13):2039-2046. LI Peng,YANG Shi-wang,WANG Yang,etal.Objective function diagonalization decoupling control of microgrid power based on relative gain analysis[J].Proceedings of the CSEE, 2014,34(13): 2039-2046. (In Chinese) [4]王成山,肖朝霞,王守相.微网中分布式电源逆变器的多环反馈控制策略[J].电工技术学报,2009,24(2):100-107. WANG Cheng-shan,XIAO Zhao-xia,WANG Shou-xiang.Multiple feedback loop control scheme for inverters of the micro source in microgrids[J].Transactions of China Electrotechnical Society, 2009, 24(2):100-107. (In Chinese) [5]DE BRABANDERE K,BOLSENS B,VAN DEN KEYBUS J,etal. A voltage and frequency droop control method for parallel inverters[J]. IEEE Transactions on Power Electronics,2007,22(4):1107-1115. [6]LI Yan,LI Yun-wei.Decoupled power control for an inverter based low voltage microgrid in autonomous operation[C]//Proceedings of the Power Electronics and Motion Control Conference.Wuhan:IEEE,2009: 2490-2496. [7]LI Yan,LI Yun-wei.Virtual frequency-voltage frame control of inverter based low voltage microgrid[C]//Proceedings of the IEEE Electrical Power & Energy Conference.Montreal:IEEE,2009:1-6. [8]周贤正,荣飞,吕志鹏,等.低压微电网采用坐标旋转的虚拟功率V/f下垂控制策略[J].电力系统自动化,2012,36(2):47-51. ZHOU Xian-zheng,RONG Fei,LV Zhi-peng,etal.A coordinate rotational transformation based virtual power V/f droop control method for low voltage microgrid[J].Automation of Electric Power Systems,2012,36(2):47-51.(In Chinese) [9]LI Yun-wei,KAO Ching-nan.An accurate power control strategy for power-electronics-interfaced distributed generation units operating in a low-voltege multibus microgrid[J].IEEE Transactions on Power Electronics,2009,24(12):2977-2988. [10]李鹏,杨世旺,殷梓恒.基于相对增益矩阵的微网稳压解耦下垂控制方法[J].中国电机工程学报,2015,35(5):1041-1050. LI Peng,YANG Shi-wang,YIN Zi-heng.Voltage stabilization and decoupling droop control method for microgrid based on RGA[J]. Proceedings of the CSEE,2015,35(5):1041-1050.(In Chinese) [11]牟晓春,毕大强,任先文.低压微网综合控制策略设计[J].电力系统自动化,2010,34(19):91-96. MOU Xiao-chun,BI Da-qiang,REN Xian-wen.Study on control strategies of a low voltage microgrid[J].Automation of Electric Power Systems,2010,34(19):91-96. (In Chinese) [12]阚加荣,谢少军,吴云亚.无互联线并联逆变器的功率解耦控制策略[J].中国电机工程学报,2008,28(21):40-45. KAN Jia-rong,XIE Shao-jun,WU Yun-ya.Research on decoupling droop characteristic for parallel inverters without control interconnection[J].Proceedings of the CSEE,2008,28(21): 40-45. (In Chinese) [13]苏玲,张建华,苗唯时,等.微型燃气轮机微网控制策略[J].高电压技术,2010,36(2):513-518. SU Ling,ZHANG Jian-hua,MIAO Wei-shi,etal.Control strategy of microturbine microgrid[J].High Voltage Engineering,2010,36(2): 513-518. (In Chinese) A Coordinate Transformation Based Power Decoupling and Restriction Control Strategy for Microgrid YAN Xiang-wu, WANG Yue-ru†, WANG Xing-hai (School of Electrical and Electronic Engineering, North China Electric Power Univ, Baoding, Hebei071003, China ) In low voltage microgrid, traditional power droop control will cause active and reactive power coupling problem. Virtual power droop control based on coordinate transformation was adopted and its decoupling characteristics, power sharing and restriction problems were studied. Relative gain analysis method was used to analyze the power coupling degree after adopting coordinate transformation. It is theoretically proved that the virtual power droop control can realize total power decoupling characteristics when the coordinate transformation matrix and line impedance have the same resistance and inductance ratio. Aiming at the problem that line impedance difference can cause uneven power sharing, a strategy was proposed, which aimed to improve power sharing accuracy by adding virtual negative impedance. In the light of the limitation of the existing power restriction range of virtual power droop control which is not equal to the actual power restriction range of the inverter, a new power restriction control strategy was proposed. Eight sections were divided for the operation points, in which the power exceeds the limits. The section number was determined according to the inverter output power and the corresponding adjustment measures were taken. Simulation results have verified the correctness and effectiveness of the proposed control strategy. microgrid;power control;coordinate transformation;virtual power;decoupling; virtual impedance;power restriction 1674-2974(2016)08-0085-07 2015-09-14 国家高技术研究发展计划(863计划)资助项目(2015AA050603);河北省自然科学基金资助项目(E2015502046);国家电网公司科学技术资助项目(SGTYHT/14-JS-188);河北省科技计划资助项目(15214307D) 颜湘武(1965-),男,湖南醴陵人,华北电力大学教授,博士生导师†通讯联系人,E-mail:wyr_ncepu@126.com TM464 A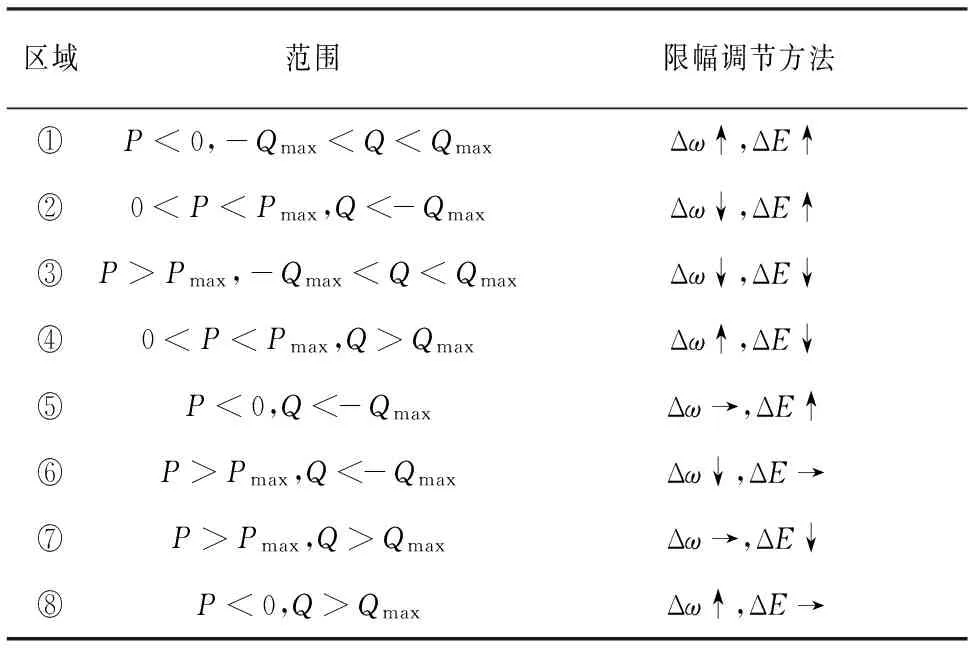
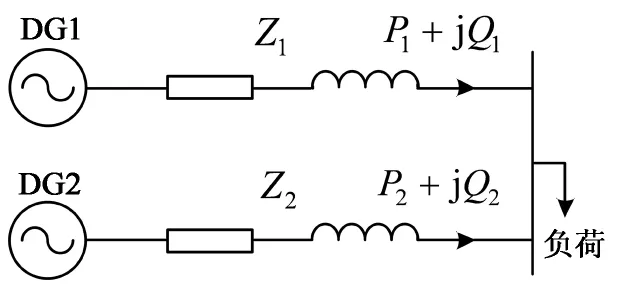
3 仿真分析
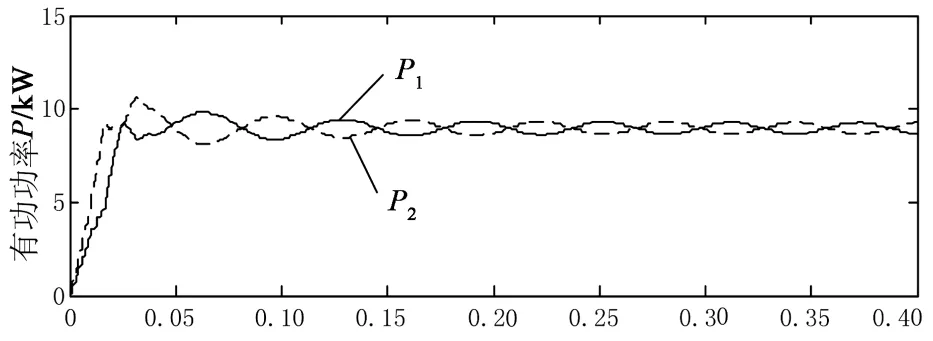
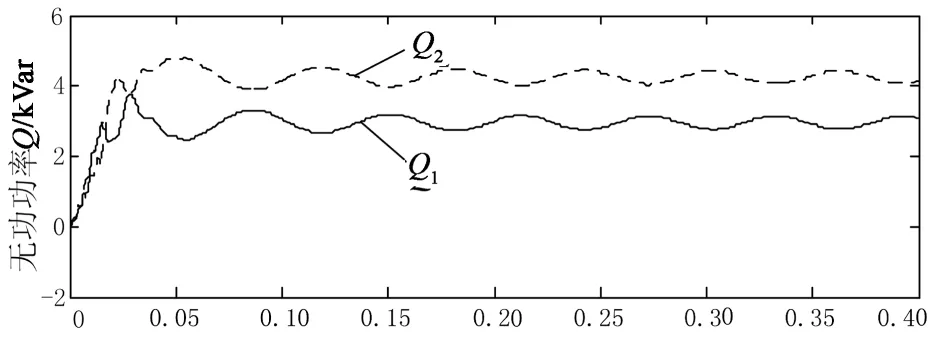
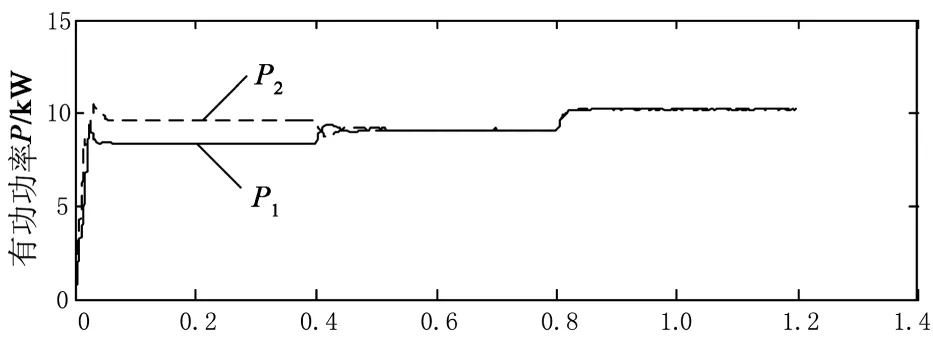
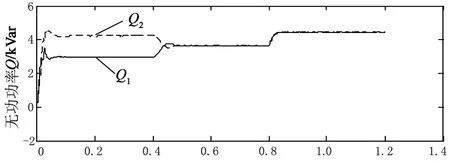
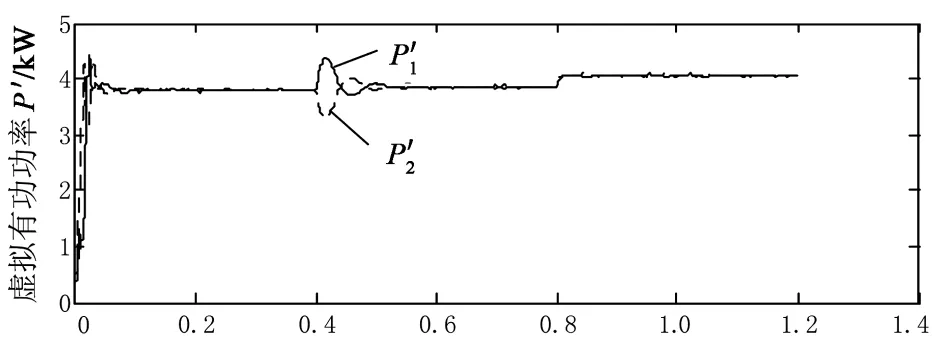
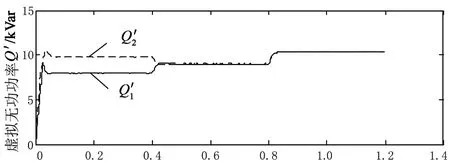
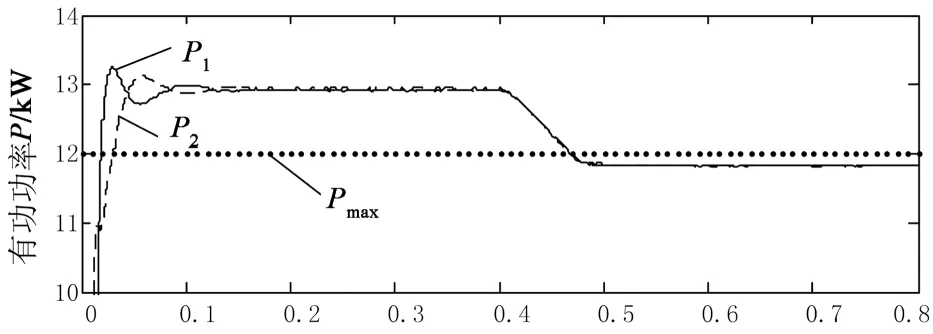

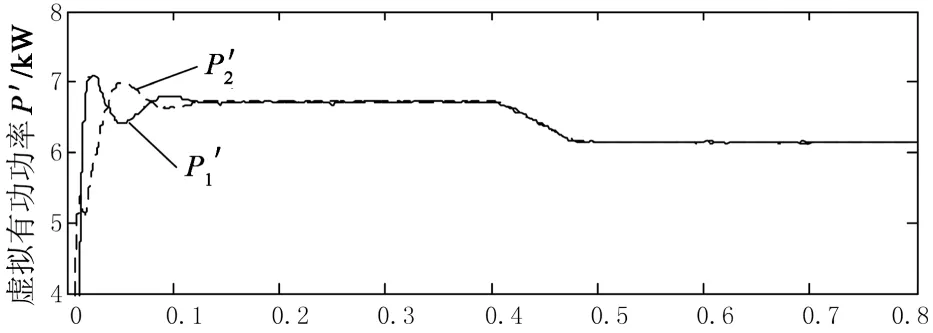

4 结 论
