质量时变系统的动载荷识别*

彭　凡，王　樑, 肖　健

(1.湖南大学 机械与运载工程学院,湖南 长沙　410082；2.北京强度与环境研究所,北京　100076)



质量时变系统的动载荷识别*

彭凡1†，王樑1, 肖健2

(1.湖南大学 机械与运载工程学院,湖南 长沙410082；2.北京强度与环境研究所,北京100076)

研究质量时变系统的动态载荷识别技术，引入广义模态概念，在初瞬时的模态空间中利用模态叠加法得到部分解耦的动力学方程，结合考虑质量变化效应的虚拟变形法和Duhamel积分，构建反演动态力的2种分析途径.一种是基于加速度反演的连锁递推格式，另一种是基于位移和加速度反演的正则化求解格式.分析2个动载荷作用下的变质量多自由度系统，利用Euler中点辛差分方法求得系统的响应，将其叠加随机噪声以模拟测点响应，然后，应用2种模态力反求格式反演动载荷.研究结果表明，连锁递推格式计算效率高，但对加速度测量噪声敏感；正则化求解格式的稳健性较高.

变质量；动态载荷；反问题；递归计算；正则化

许多工程领域存在质量等振动参数随时间发生变化的动力学问题[1-5].质量时变系统的动力学响应分析方法主要包括2类，一类是直接积分法，包括Newmark法和各类差分算法[6]；另一类是基于短时时不变假设的模态叠加法[7-8].与动力响应分析相对应的是质量时变振动系统的载荷反求，如考虑质量快速减少的运载工具的脉动推力反求，这在工程上也是非常有意义的课题.针对时不变结构的动态载荷识别，已经发展了较为丰富的方法与技术[9].然而，关于时变结构的动态载荷识别方法的研究还较少，张青霞等[10]将车桥系统视为质量时变系统，移动荷载的反求转化为移动质量的识别，基于虚拟变形法识别移动质量.

本文研究质量时变系统载荷识别方法，在初始模态空间中，结合模态叠加和虚拟变形技术，构造模态力反求格式，经模态转换得到相应的物理量.分析变质量多自由度系统，首先由差分法计算受激振动响应，将其叠加噪声以模拟测量信号，然后，反求模态力得到动载荷，比较2种反求格式的有效性及优劣.

1　初始模态空间中的模态力计算格式

1.1基于初始模态求解时变质量系统的动力学方程

考虑自由度数为n的变质量系统，其动力学方程为[7]：

(1)

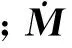
(2)

式中：M0为初始质量矩阵；ΔM(t)为与时间相关的增量质量矩阵，即

ΔM=M(t)-M0.

(3)

考虑初始振动参数构成的自由振动系统，有

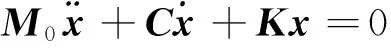
(4)

采用比例阻尼模型，C=αM0+βK.将基于式(4)得到的振型空间称为初始模态空间，取前面ns阶模态，相应的模态矩阵表示为Φ，其维数为n×ns.对式(2)所描述的振动系统，进行如下变量转换:

x=Φq.

(5)

式中:q为初始模态空间中的ns个模态坐标组成的列向量.将式(5)代入式(2)，两边同时左乘ΦT，得到

(6)

式中:ωi和ξi(i=1,2,…,ns)分别为初始瞬时的频率和模态阻尼比;diag(…)表示对角矩阵.右端各项分别为:

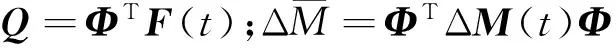
(7)

式中:Q为初始模态空间中的模态力.

式(6)中若右边的质量改变项为零，则对应的结构为初始结构.如果已知初始结构的响应，根据虚拟变形法， 结构模型变化后的响应可通过引入的虚拟力求出[11].由此，在零初始条件下，可由初始系统的Duhamel积分得到式(6)的解为:

(8)

式中:H(t)为单位脉冲响应函数构成的对角矩阵;H(t) =diag(hi)，其中的对角项为脉冲响应函数.

(9)

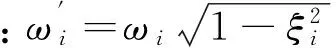
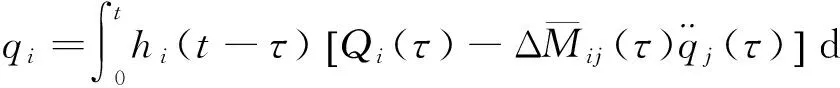
(10)

下面构建由已知响应求模态力的2种反演途径.

1.2模态力反演的连锁递推格式

引入以下参向量:

(11)

由式(8)导出模态加速度为:

(12)

式中:I为n阶单位矩阵.

针对式(12)构造等步长递推格式，时间步长为Δt，第l步(l=0，1，2，…)所对应的时间tl=lΔt，采用梯形求积法离散，可得如下递推式:

l ≥1，

(13a)

(13b)

式中:μi=e-ξiωiΔt;上标括号中的l与l-1分别表示第l和l-1递推步.结合式(12)和式(11)，将当前时间步的模态力表示为:

(14)

式中:si=1-ξiωiΔt;

1.3模态力反演的正则化求解

在式(10)中，令

(15)

将式(10)的求积区间划分成长为Δt的m等分，各节点对应的时间为tl=lΔt,l=0，1,…,m，用矩形求积离散卷积得到:

(16)

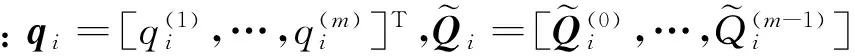
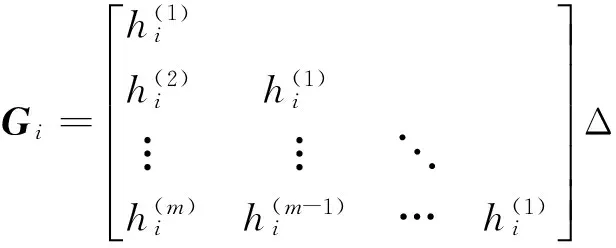
采用截断奇异值分解的正则化方法[12]反求式(16)的模态力.首先将核函数矩阵Gi作奇异值分解.

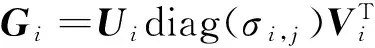
(17)

式中:σi,j(j=1,2, …,m)为奇异值;Ui和Vi分别为左奇异值和右奇异值酉矩阵.引入正则化算子f(λ, σi,j)，当小奇异值σi,j趋于零，f(λ, σi,j)/ σi,j也趋于零，由此可得到实际载荷的一个稳定的近似估计.

(18)

式中:λi为正则化参数.取

(19)

采用广义交叉验证准则[13](GCV)得到λi，为此，构造如下函数:

(20)

式中:E=I-Gi[GiTGi+λiI]-1GiT;tr(E)表示E的迹.H(λi)的极小值点就是正则化参数.

1.4动载荷分析

设振动系统同时作用了待识别的动态载荷Fi(i=1,2, …,ν)，则由式(7)的第1式，将模态力写为:

(21)

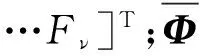
(22)

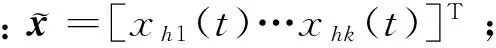
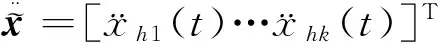
Ψ由Φ中相应的k个列向量组成.结合最小二乘，得初始模态空间中的模态位移与模态加速度分别为:

(23)

利用式(14)或(18)，反求模态力，最后，再根据式(21)给出动态载荷的最小二乘解:

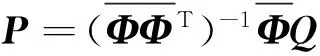
(24)

2　算例及方法讨论

考虑图1所示的n个自由度的质量时变系统，第i个质点的初始质量为m0i=40[2+i(-1)i/n]，单位为kg；弹簧刚度Ei=15×105[2+i(-1)(i+1)/n]，i=1,…,n，单位为N/m.各质点以速率m0i×0.8/te减少其质量，其中te表示计算时间.在质点1和6质点上分别施加动载荷F1与F2，单位为N，分别有:

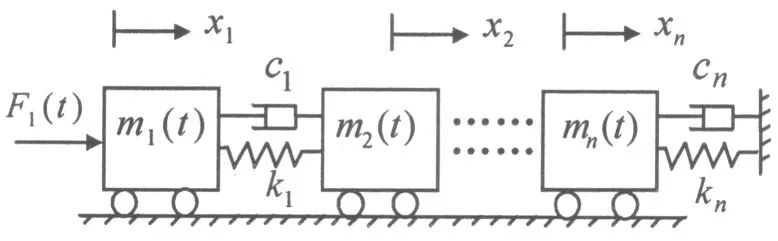
图1　n自由度变质量系统

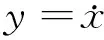
(25)

用Euler中点辛差分格式[6-7]求解式(25)，有

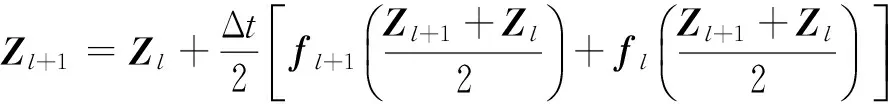
(26)

由式(25)和(26)，得到下面计算格式:

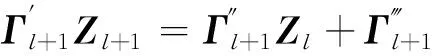
(27)

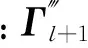
考虑n=16的系统，在初始模态空间中的固有频率为2.65～67.9Hz.设定零初始条件，由式(27)进行正问题分析，取时间步长Δt=0.002s，求得响应后，叠加随机噪声作为模拟实测量.

χerr=χ+ηstd(χ)Nr.

(28)

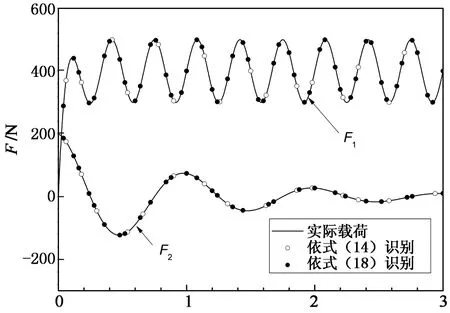
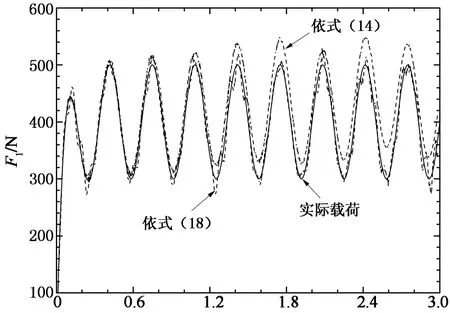
式中:χerr为叠加了噪声的模拟实测量;χ为正问题计算所得响应;std(χ) 为对应的标准差;η为噪声水平; Nr为-1～1的随机数.然后，取前8阶模态叠加进行载荷反演，由8个质点1,2,5,6,9,10,12和14的响应反求2个动态力.不考虑测量噪声，即η=0，分别基于模态力的连锁递推反求(式(14))和正则化反求(式(18))得到的动载荷结果如图2所示，由图2可见，反演载荷与实际载荷吻合.再考虑η=2%，2个动载荷的识别结果分别如图3与图4所示，可见，考虑测量噪声的影响后，采用式(14)进行反求时，在最初阶段，识别结果与实际载荷相差很小，但随时间增大，两者的偏离越来越明显.递推计算对初值敏感，产生明显累积误差，其原因在于式(14)中模态力前面的系数项si小于1，每一步都放大了误差.图3和4同时表明，基于正则化反演所得结果均是在实际载荷值附近波动，动载荷随时间变化的趋势与实际情形相同，正则化反演对测量噪声有较好的抑制作用.考察式(15)可见，由于质量时变项的存在，模态力反求后，其精度仍然受到加速度测量噪声的直接影响，这是导致动载荷反演结果在实际载荷附近波动的主要原因，对测量信号进行滤波，尽量减少噪声污染是提高识别精度的一条重要途径.从计算效率来考虑，连锁递推的计算量小，而正则化反演需对每阶模态力求高阶代数方程组，相应的计算量显著增加.

t/s

t/s

t/s

3　结　论

在初始模态空间中建立变质量系统动载荷识别途径.以变质量多自由度系统的动态激励反演为算例，考察所构造的2种模态力反求格式的稳健性和耐噪性.1)利用离散Duhamel积分构造的模态力连锁递推计算仅需加速度测量信号，且计算量小，但容易产生误差累积导致反演结果对初值敏感.2)利用位移的Duhamel积分离散进行模态力的正则化求解格式需要位移、加速度测量信号，稳健性较第1种方法强，计算量较大.

[1]JOSHIA.Freevibrationcharacteristicsofvariablerocketshavinglargeaxialthrust/acceleration[J].JournalofSoundandVibration,1995,187(4):727 -736.

[2]VANDERBURGHAHP,HARTONO,ABRAMIANAK.Anewmodelforthestudyofrain-wind-inducedvibrationsofasimpleoscillator[J].InternationalJournalofNon-LinearMechanics, 2006, 41(3): 345-358.

[3]沈国辉,徐晓斌,楼文娟,等.导线覆冰脱冰有限元模拟方法的适用性分析[J]. 工程力学, 2011, 28(10):9-15.

SHENGuo-hui,XUXiao-bin,LOUWen-juan,et al.Applicabilityanalysisoffiniteelementmethodologiestostimulatetheice-accretingandice-sheddingontransmissionlines[J].EngineeringMechanics, 2011, 28(10):9-15.(InChinese)

[4]曹国华,朱真才,彭维红,等.变质量提升系统钢丝绳轴向-扭转耦合振动特性[J]. 振动与冲击, 2010, 29(2):64-68.

CAOGuo-hua,ZHUZhen-cai,PENGWei-hong,et al.Axial-torsioncouplingvibrationcharacteristicsinelevatesystemwithvariablemass[J].JournalofVibrationandShock, 2010, 29(2):64-68. (InChinese)

[5]廖剑晖,由小川,吕海波,等.发展时变附加质量方法模拟飞行器出水过程[J]. 工程力学,2012, 29(4):202-223.

LIAOJian-hui,YOUXiao-chuan,LVHai-bo, et al.Developmentofatime-varyingaddedmassmethodinthesimulationsofthewater-exitprocessofunderwatervehicle[J].EngineeringMechanics, 2012, 29(4):202-223.(InChinese)

[6]邢誉峰,杨蓉.动力学平衡方程的Euler中点辛差分求解格式[J]. 力学学报, 2007, 39(1): 100-105.

XINGYu-feng,YANGRong.ApplicationofEulermidpointsymplecticintegrationmethodforthesolutionofdynamicequilibriumequations[J].ChineseJournalofTheoreticalandAppliedMechanics, 2007, 39(1): 100-105.(InChinese)

[7]邢誉峰,谢珂,潘忠文.变质量系统振动分析的两种方法[J]. 北京航空航天大学学报,2013, 39(7):858-862.

XINGYu-feng,XIEKe,PANZhong-wen.Twomethodsforvibrationanalysisofvariable-masssystems[J].JournalofBeijingUniversityofAeronauticsandAstronautics, 2013, 39(7):858-862.(InChinese)

[8]于开平, 庞世伟, 赵婕. 时变线性/非线性结构参数识别及系统辨识方法研究进展[J]. 科学通报, 2009,54(20):3147-3156.

YUKai-ping,PANGShi-wei,ZHAOJie.Advancesinmethodoftime-varyinglinear/nonlinearstructuralsystemidentificationandparameterestimate[J].ChineseScienceBulletin, 2009, 54(20): 3147-3156.(InChinese)

[9]SANCHEZJ,BENAROYAH.Reviewofforcereconstructiontechniques[J].JournalofSoundandVibration, 2014,333(14):2999-3018.

[10]张青霞,段忠东,JANKOWSKL.基于虚拟变形法的车-桥耦合系统移动质量识别[J].力学学报, 2011, 43(3):598-610.

ZHANGQing-xia,DUANZhong-dong,JANKOWSKL.Movingmassidentificationofvehicle-bridgecoupledsystembasedonvirtualdistortionmethod[J].ChineseJournalofTheoreticalandAppliedMechanics, 2011, 43 (3): 598-610.(InChinese)

[11]KOLAKOWSKIP,WIKLOM,HOLNICKI-SZULCJ.Thevirtualdistortionmethod—aversatilereanalysistoolforstructuresandsystems[J].StructuralandMultidisciplinaryOptimization, 2008, 36(2):217-234.

[12]HANSENPC.TruncatedSVDsolutionstodiscreteill-posedproblemswithill-determinednumericalrank[J].SIAMJournalonScientificandStatisticalComputing,1990,11(3):503-518.

[13]GOLUBGH,HEATHM,WAHBAG.Generalizedcross-validationasamethodforchoosingagoodridgeparameter[J].Technometrics, 1979,21(2):215-223.

Identification of Dynamic Loads in Mass-variable System

PENG Fan1†，WANG Liang1，XIAO Jian2

(1. College of Mechanical and Vehicle Engineering，Hunan Univ,Changsha,Hunan410082，China;2.Research Institute of Beijing Structure and Environment Engineering,Beijing100076，China )

The technique of the load identification of mass variable system was studied. The generalized modal concept applied on time-varying system was introduced, and the method of modal superposition was used to give dynamic equations with partially decoupled in initial modal space defined at initial instant. Based on both virtual distortion method (VDM) accounting for the effect of mass change and the Duhamel integration in initial modal space, two approaches to identify modal forces were constructed: one is the recursive calculation pattern formulated on the basis of modal acceleration, and the other is the regularized solution by the direct discretization of Duhamel integration with modal displacement and acceleration. A mass variable system with 16 degrees of freedom subjected to two external loads was analyzed. The responses were calculated by applying Euler midpoint symplectic difference method and added with random noise to simulate measured signals. Two dynamic loads were identified by two inversion approaches of modal forces. The comparison of results has indicated that regularized solution format has a higher numerical robust than the recursive calculation pattern, but the latter is sensitive to the noise of measurement.

time-varying mass;dynamic loads;inverse problems; recursive calculation; regularization

1674-2974(2016)08-0052-05

2015-04-17

湖南省自然科学基金资助项目(11JJ3001)

彭凡(1963-)，男，湖南湘乡人，湖南大学教授†通讯联系人，E-mail:fanpeng@hnu.edu.cn

O326;O347.1

A