基于小波变换的信号时频分析与重构
2016-09-08董航胡云鹏
董航 胡云鹏
【摘要】 作为一种不定频的扩频通信系统,跳频通信系统由于其载波在收发双方预先约定好伪随机序列的前提下一定频段内并不固定,故有较强的抗干扰性、低截获概率。而对于跳频信号的盲识别,其技术的关键核心是利用有效的时频分析方法对信号在不同时段的载波频段进行分析并对信号进行重构,从而对信号进行解调,从而获取信号中的信息。首先,确定合理的尺度参数和小波的类型等;其次,对所接收到的跳频信号利用小波变换法得到信号的时频参数;最后,确定分解层次,用小波对信号进行分解得到细节分量、近似分量。并去掉合理的细节分量从而得到较好的重构信号。
【关键词】 跳频通信 小波变换 时频分析 信号重构
Time frequency analysis and reconstruction of signals based on Wavelet Transform
【Abstract】As a spread spectrum telecommunication system, frequency hopping telecommunication system has strong anti –interference and low probability of intercept due to the carrier is not fixed in a specified frequency in the sending and receiving sides when both sides agreed in advance under one type of pseudo random sequence bands. The key core of this technology are using effective time-frequency analysis method to analyze the signal in different periods of carrier frequency band and the reconstruction of signal, because by this way it will be easier to demodulate the signal and get the information in the signal. Firstly, determine the reasonable scale parameters with the wavelet type, etc.; secondly, use wavelet transform to get the signal timefrequency parameters of the receiving frequency hopping signal; finally, determine the decomposition level and then use wavelet to decompose the detail components and the approximate component of signal, And get rid of the reasonable detail component to get better reconstructed signal.
【Key words】Frequency hopping telecommunication; Wavelet transform; Time frequency analysis; Signal reconstruction
一、引言
本文的研究目标是如何有效地应用时频分析算法得到不同时段的载波频段,并对信号进行分解。对于时频分析方法的选择会对信号的分析、识别与构造结果起着重要的影响。
二、基本原理
2.1 识别原理
不同于已知跳频频段所符合的伪随机序列,盲识别首先要通过时评分析得到跳频信号的参数,之后在对信号进行重构后进行变频解调。
2.2 特征参数
(1)跳频带宽;(2)跳频频率数;(3)跳频速率;(4)跳频周期
三、小波分析
3.1 小波变换识别信号
在小波变换中,所用小波的基小波函数的类型不具有唯一性,对于同样的信号采用不同小波分析的结果会相差甚远。本文用对于分析正弦信号性能较好的Morlet小波进行分析。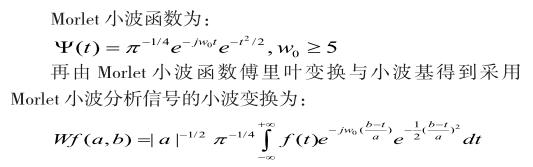
3.2 降噪与信号重构
小波去噪原理
一般来说,噪声信号多包含在具有较高频率细节中,在对信号进行了小波分解之后,再利用门限阈值等形式对所分解的小波系数进行权重处理,然后对小信号再进行重构即可达到信号去噪的目的。具体步骤为:
(1) 一维信号的小波分解,选择一个小波并确定分解的层次,然后进行分解计算。
(2) 小波分解高频系数的阈值量化,对各个分解尺度下的高频系数选择一个阈值进行软阈值量化处理。
(3) 一维小波重构,根据小波分解的最底层低频系数和各层高频系数进行一维小波的重构。
Mallat算法的信号分解
本文重点研究基于Mallet算法分解重构小波信号。
根据多分辨率理论,得出结论:
四、仿真结果
在仿真中,采用采用的模拟信号源的参数为:信道通带:5000-25000HZ;信道带宽:20000HZ跳频速率:500跳/秒;跳频频率数:200对信号添加高斯白噪声,以模拟真实信号的噪声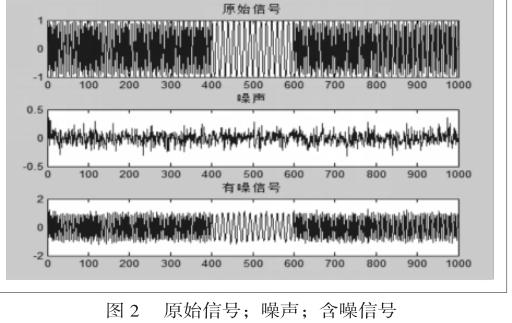
通过Morlet小波变换对添加了噪声的信号进行时频分析,小波变换的参数为:
小波类型:复Morlet小波;小波带宽:3HZ;小波中心频率: 3HZ
利用MATLAB中的小波变换工具箱进行编程,得到接收到信号的时频图,并与信源信号的理想时频图进行比较,可以发现时频分析较好的识别出了跳频信号的跳变参数。
对接收到的信号进行分解。本文采用db4小波对信号进行分解,为了保证信号的重构质量与系统的反应速度,采用4层分解。得到了各层信号的细节分量与近似分量。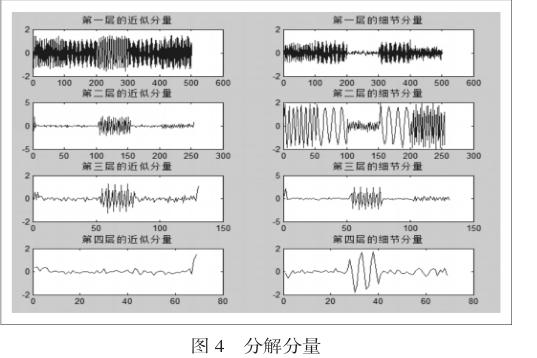
五、结束语
本文所采用的Morlet小波变换对跳频参数估计有着较好的性能,在面对不同频段的扩频跳频系统有着灵活的应用前景。
参 考 文 献
[1]冯涛. 基于时频分析的跳频通信侦察技术研究[D].北京邮电大学,2012.
[2]罗朝洪. 跳频信号的参数估计和调制识别[D].电子科技大学,2009.
[3]徐博尧,杨刚,李欣欣. 小波变换的时频分析及其在实际中的应用[J]. 中国传媒大学学报(自然科学版),2011,02:79-83+59.
[4]刘丽娟. 时频分析技术及其应用[D].成都理工大学,2008.
