基于近似熵和集成经验模态分解的转子多故障诊断方法研究

韩中合　徐搏超　朱霄珣　焦宏超

华北电力大学，保定,071003



基于近似熵和集成经验模态分解的转子多故障诊断方法研究

韩中合徐搏超朱霄珣焦宏超

华北电力大学，保定,071003

为了提高汽轮机转子多故障分类的准确率，提出一种集成经验模态分解(EEMD)、近似熵和支持向量机相结合的多状态分类方法。首先进行EEMD得到各频段的单分量信号；再求出熵值作为故障信号的特征向量输入到基于二叉树的支持向量机中实现多状态分类。对比近似熵、模糊熵和能量法这三种方法，实验结果验证了利用EEMD和熵理论相结合的方法量化故障信号非线性特征的正确性。同时也表明在欧氏空间中，近似熵值组成的特征向量彼此间的距离最远，分类效果也最好。

集成经验模态分解；近似熵；支持向量机；多故障诊断

0　引言

对汽轮机转子不同故障状态进行准确的辨别是保证维修工作顺利进行的关键，同时也可以避免重大的工业生产损失。状态判别在本质上属于模式识别[1]问题，支持向量机[2](supportvectormachine,SVM)作为一种新兴的方法，相比于专家系统和神经网络，在小样本处理方面有着独特的优势[3]，被广泛运用于转子的故障诊断中。

支持向量机分类的核心思想是把低维样本的特征向量通过核函数映射到高维空间再寻找最优超平面对其进行分类[4]。在高维空间内，不同类别的特征向量彼此间的距离越远，SVM分类准确率越高。因而提取出能反映该类故障的信号特征值，构建高品质的训练样本至关重要。

转子的故障信号具有很强的非线性，集成经验模态分解[5](ensembleempiricalmodedecomposition，EEMD)作为一种自适应时频分析方法，可以实现复杂的多分量信号特征的分离，因此适用于转子故障信号的分解。但分解出单分量信号无法直接作为“特征”应用于转子故障的模式识别中。由于转子发生不同类型的故障时，在工频的倍频区域，信号的复杂度变化明显，因而分解出的单分量信号的复杂性差异明显。熵理论[6]具有可以量化信息复杂度的特点，近年来得到广泛应用。因此可以计算熵值作为非线性特征值。

基于此，本文对EEMD分解后的本征模态函数(intrinsicmodefunction,IMF)计算近似熵值，进而组成特征向量。通过基于二叉树算法的SVM模型进行多故障分类。作为对比，本文还使用模糊熵和能量法提取故障特征值，结果表明使用近似熵值作为特征向量，不同类型的故障样本彼此间的距离最远，同时SVM分类效果最好。

1　EEMD和近似熵相结合的信号特征提取方法

1.1EEMD原理介绍

为了克服经验模态分解(empiricalmodedecomposition，EMD)中存在的模态混叠现象[7]，文献[8]提出了一种加入辅助白噪声的信号处理方法，即EEMD方法，其步骤如下：

(1) 在原始信号x(t)中加入均方根相对较小的高斯白噪声序列nm(t)得到混合信号xm(t)(m=1,2,…，n)。

(2)对xm(t)进行多次EMD分解，每次得到固定个数的IMF分量Cpm,p=1,2,…,P。

(3)每次在x(t)中加入不同的白噪声序列，重复步骤(1)和步骤(2)n次。

(4)分别计算p个Cpm的平均值Cp，将p个Cp作为EEMD的IMF分量。

1.2近似熵算法

为了定量描述信息的复杂程度，Pincuss[9]提出了近似熵的概念。由于近似熵值对数据数量依赖性较小、结果稳定，因此广泛应用于旋转机械故障诊断等方面的工程应用中。近似熵值越大说明给定序列越复杂。

对于给定的序列si(i=1,2,…，N)，求解过程如下：

(1)将序列si按顺序组成m维矢量:

S(i)=(si,si+1,…,si+m-1)

(1)

i=1，2，…，N-m+1

(2)定义距离Dm[Si，Sj]为Si、Sj对应元素差值的绝对值中较大的一个，即

(2)

j=1，2，…，N-m+1

计算出每一个Si与其余矢量Sj之间的距离。

(3)

(6)当N取有限值时，近似熵ApEn(m,r)估计值为

ApEn(m,r,N)=Φm(r)-Φm+1(r)

(4)

这里，嵌入维数m和相似容限r在很大程度上影响到近似熵值。根据经验：一般m=2，r=0.1-0.25QSD。其中，QSD为原始数据si的标准差。

1.3基于EEMD与近似熵的样本特征构造方法

文献[10]中显示：转子不平衡的频谱特征主要是基频(工作频率)，其他频率成分相对较少。转子不对中频谱图上一、二、三倍频处一般会出现高峰，且二倍频要高于一倍频。油膜涡动的典型频谱特征为半频、一倍频稳定存在；动静碰磨频域特征突出表现为多次倍频增加，故障信号中出现高次频与次高频成分。

对故障信号进行EEMD，通过实验分析得出以下结论：故障特征大部分集中在前几阶IMF分量中。本文选取前3阶IMF分量计算其近似熵代表高频、工频、半频的特征，其余IMF分量之和的近似熵作为低频特征值。把高频、工频、半频、低频特征值组合在一起作为该故障的特征向量，构建训练样本，并输入SVM进行训练。

对上述每一种转子故障信号按图1 所示过程进行故障特征提取。

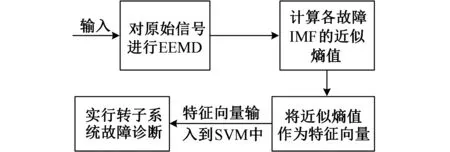
图1　故障特征提取流程图

2　基于二叉树的SVM多故障诊断

2.1支持向量机

支持向量机是基于统计学中VC(Vapnik-Chervonenkis)维理论，以结构风险最小化为目标的学习模型[11-12]。其特点是通过核函数将低维数据投射到高维空间中，避免了大量的高维运算。在高维空间中寻找最优超平面。如果某个超平面能够分隔开训练集合中所有不同类别的“样本点”，并且不同类别中距离超平面最近的“样本点”到此超平面的距离达到最大，则此超平面即为所求(最优超平面)。不同类别中距离最优超平面最近的样本点称之为“支持”向量。与传统方法的模式识别相比，SVM不需要选取合适的判别函数形式，也不需要进行相关参数的调整和选取。

2.2基于二叉树的SVM多分类方法

支持向量机只能区分两类样本，但是在实际问题中更常见的是多分类问题。常用的多分类算法有一对一算法、一对多算法、有向无环图和二叉树。

在上述四种方法中，二叉树算法所需的支持向量机最少，又不存在不可分区域，因此本文采用二叉树算法[13]：该算法先挑出一种类别作为A类，把剩余的所有类别都划为B类。再在B类中挑出一种类别作为下一级的A类，剩余的类别再次作为下一级B类。重复上述步骤，直到实现类别与节点之间的一一对应。

以本文5种故障的分类问题为例，其二叉树结构如图2所示。

图2　二叉树5类分类图

3　实验应用及分析

3.1整体流程介绍

本文提出的故障多分类诊断方法具体步骤如下：

(1)将故障信号进行EEMD，得到各频段分量。

(2)计算各频段分量熵值作为特征值，按照对应频段组建特征向量。

(3)基于二叉树算法用多个SVM构建系统实现多分类。通过对训练样本进行学习，获得分类能力。

(4)按照步骤(1)、步骤(2)提取故障信号的特征向量输入到已经完成训练的多分类系统中进行分类，实现故障诊断。

3.2实验过程及结果

利用BentleyRK4转子实验台(图3)对汽轮机转子正常状态和转子不平衡、转子不对中、动静碰磨、油膜涡动四种常见振动故障进行实验模拟。实验台设置转速为3000r/min，采样频率为1280Hz，采样点数为1024。对每种状态采集数据20组，前10组作为训练样本，后10组作为测试样本。

图3　Bentley RK 4转子实验台

首先利用近似熵、模糊熵[14]和能量法计算出代表每种状态训练样本的特征向量，如表1所示。

表1　转子系统故障训练样本特征向量

构建训练样本后输入到基于二叉树的SVM多分类模型中进行训练。再按照上述步骤构建测试样本，使用已经完成训练的多分类模型对测试样本进行分类。三种信号特征量提取方法的最终SVM分类结果见表2。

表2　不同特征量的SVM分类结果

从表2可以看出，采用本文所提出的近似熵特征提取方法进行SVM模式识别，准确率高达98%，模糊熵为80%，能量法为60%。

3.3故障信号特征量化方法评估

对于待分类的样本，彼此的特征向量在空间上距离越远，分类模型越容易对它们进行区分。因此，比较不同方法计算出的样本故障特征向量在空间距离的远近可以在一定程度上评估该方法量化非线性特征能力的优劣。

针对本文使用的近似熵、模糊熵和能量法，以训练样本为例，首先求出三种方法计算得到的不同状态之间特征向量的类心距s(i,j)(其中i，j=1，2，3，4，5。i=1代表动静碰磨状态；i=2代表转子不对中状态；i=3代表转子不平衡状态；i=4代表油膜涡动状态；i=5代表正常状态)(表3)，然后求出这两种状态的特征向量的半径和R(i,j)，最后求出两者的差值Δ(i，j)，Δ(i，j)= s(i，j)- R(i，j) 。计算结果如表4所示。

表3　不同特征量类心距s(i,j)

表4　不同特征量类型的Δ(i,j)

由表4可以看出，近似熵求出的转子5种状态训练样本特征向量的Δ(i，j)值最大，模糊熵次之，能量法最小。与上述实验结果一致，同时也验证了本文提出的基于熵理论的非线性特征量化方法评估准则的正确性。

4　结论

(1)近似熵理论可以表征信号的非线性特征。相对于模糊熵和能量法，近似熵计算出的故障特征可以在欧氏空间中使不同类的故障间具有更好的区分度。

(2)通过本文实验对比，计算近似熵、模糊熵和能量法得到的特征向量在基于二叉树的SVM多分类故障诊断模型中识别率分别是98%、80%和60%。因此EEMD和近似熵相结合的故障信号诊断方法更适合工程应用。

[1]张秀玲，张少宇，赵文保，等. 板形模式识别的多输出最小二乘支持向量回归机新方法[J]. 中国机械工程，2013,24(2)：258-263.

Zhang Xiuling, Zhang Shaoyu, Zhao Wenbao, et al. A Novel Method for Flatness Pattern Recognition via MLSSVM[J]. China Mechanical Engineering, 2013,24(2)：258-263.

[2]古莹奎，承姿辛，朱繁泷. 基于主成分分析和支持向量机的滚动轴承故障特征融合分析[J]. 中国机械工程，2015,26(20):2778-2783.

Gu Yingkui, Cheng Zixin, Zhu Fanlong. Rolling Bearing Fault Feature Fusion Based on PCA and SVM[J]. China Mechanical Engineering, 2015,26(20):2778-2783.

[3]曾鸣，杨宇，郑近德，等. 基于LCD和KNNCH分类算法的齿轮故障诊断方法[J].中国机械工程， 2015,25(15)：2049-2054.

Zeng Ming, Yang Yu, Zheng Jinde, et al. Fault Diagnosis Approach for Gears Based on LCD and KNNCH Classification Algorithm[J]. China Mechanical Engneering， 2015,25(15)：2049-2054.

[4]张爱，陆有忠，郑璐石. 迅速崛起的机器学习技术——支持向量机[J].宁夏工程技术，2004，3(2)：136-140.

Zhang Ai，Lu Youzhong，Zheng Lushi. Rapidly Emerging Machine Learning Technology—Support Vector Machine[J]. Ningxia Engineering Technology, 2004，3(2)：136-140.

[5]Wu Z，Huang N E. A Study of the Characteristics of White Noise Using the Empirical Mode Decomposition Method[J].Proceedings of the Royal Society A，2004，460(2046):1597-1611.

[6]郑近德，程军圣，杨宇. 基于改进的ITD和模糊熵的滚动轴承故障诊断方法[J]. 中国机械工程，2012，23(19)：2372-2377.

Zheng Jinde, Cheng Junsheng, Yang Yu. A Rolling Bearing Fault Diagnosis Method Based on Improved ITD and Fuzzy Entropy[J]. China Mechanical Engneering，2012，23(19)：2372-2377.

[7]胡爱军，孙敬敬，向玲. 经验模态分解中的模态混叠问题[J]. 振动、测试与诊断，2011，31(4)：429-434.

Hu Aijun, Sun Jingjing, Xiang Ling. Mode Mixing in Empirical Mode Decomposition[J]. Journal of Vibration, Measurement & Diagnosis, 2011，31(4)：429-434.

[8]Wu Zhaohua，Huang N E. Ensemble Empirical Mode Decomposition：a Noise-assisted Data Analysis Method [J]. Advances in Adaptive Data Analysis， 2009，1(1)：1-41.

[9]Pincuss S M. Approximate Entropy as a Measure of System Complexity[J]. Proceeding of the National Academy Sciences, 1991，88(6)：2297-2301.

[10]王延博.汽轮发电机组轴系低频振动故障特征及其诊断实例[J].热力发电，2005(1):32-35.

Wang Yanbo. Fault Characteristics of Low Frequency Vibration of Turbine Generator Set and Its Diagnosis Example[J]. Thermal Power Generation, 2005(1):32-35.

[11]徐启华，师军．基于支持向量机的航空发动机故障诊断[J]．航空动力学报，2005，20(2)：298-302．

Xu Qihua，Shi Jun. Aeroengine Fault Diagnosis Based on SVM[J]. Journal of Aviation Power，2005，20(2)：298-302．

[12]吴虎胜，吕建新，吴庐山，等．基于EMD和SVM的柴油机气阀机构故障诊断[J].中国机械工程，2010,21(22)：2710-2714.

Wu Husheng, Lü Jianxin, Wu Lushan, et al. Fault Diagnosis for Diesel Valve Train Based on SVM and EMD[J]. China Mechanical Engneering，2010,21(22)：2710-2714.

[13]Takahashi F，Abe S . Decision-tree-based Multiclass Support Vector Nachines [C]//Proceedings of the 9th International Joint Conference on Networks. Singapore：IEEE Press，2002:1418-1422.

[14]杨宇，潘海洋，程军圣. 基于LCD降噪和VPMCD的滚动轴承故障诊断方法[J].中国机械工程，2013,24(24):3338-3344.

Yang Yu, Pan Haiyang, Cheng Junsheng. A Rolling Bearing Fault Diagnosis Method Based on LCD De-noising and VPMCD[J]. China Mechanical Engneering, 2013, 24(24): 3338-3344.

(编辑王艳丽)

ResearchonMulti-faultDiagnosisofRotorBasedonApproximateEntropyandEEMD

HanZhongheXuBochaoZhuXiaoxunJiaoHongchao

NorthChinaElectricPowerUniversity,Baoding,Hebei,071003

Forthepurposeofaccurateidentificationoftheturbinerotormulti-faultstates,adiagnosismethodwasputforwardbasedontheEEMD,approximateentropyandSVM.Firstly,thefaultsignalsweredecomposedtoanumberofintrinsicmodefunctions(IMFs)byEEMDmethod,thencalculatingentropyofIMFsasthefeaturevectortoconstructsamplesforbinarytreeSVMformulti-stateclassification.Thispapercomparedwithapproximateentropy,fuzzyentropyandenergymethod.TheexperimentalresultsverifythecorrectnessofquantifyingthenonlinearcharacteristicsoffaultsignalswithEEMDandentropytheory.TheyalsoindicatethatthefeaturevectorsbasedonapproximateentropyarefarthestfromeachotherinEuropeanspace,andtheclassificationaccuracyisthehighest.

ensembleempiricalmodedecomposition(EEMD);approximateentropy;supportvectormachine(SVM);multi-faultdiagnosis

2015-11-17

中央高校基本科研业务费专项资金资助项目(2015MS102)；国家自然科学基金资助项目(50676031)

TK267

10.3969/j.issn.1004-132X.2016.16.010

韩中合，男，1964年生。华北电力大学能源动力与机械工程学院教授、博士研究生导师。主要研究方向为设备状态监测与故障诊断。发表论文200余篇。徐搏超，男，1992年生。华北电力大学能源动力与机械工程学院硕士研究生。朱霄珣，男，1985年生。华北电力大学能源动力与机械工程学院讲师、博士。焦宏超，男，1990年生。华北电力大学能源动力与机械工程学院硕士研究生。