车体设计参数对车体垂向弯曲振动频率的灵敏度分析

王长科　阳光武　朱　涛　于金朋

1.西南交通大学牵引动力国家重点实验室，成都，6100312.中车唐山机车车辆有限公司，唐山，064000



车体设计参数对车体垂向弯曲振动频率的灵敏度分析

王长科1阳光武1朱涛1于金朋2

1.西南交通大学牵引动力国家重点实验室，成都，6100312.中车唐山机车车辆有限公司，唐山，064000

采用基于灵敏度分析的车体垂向弯曲刚度优化方法，对车体结构关键参数进行了灵敏度分析，确定了关键设计变量与系统响应的关系，从而得到了结构设计变量(车体结构关键参数)对目标约束函数(车体一阶垂向弯曲振动频率)影响的变化梯度。首先，由欧拉-伯努利梁垂向振动微分方程，结合初始条件和边界条件，得到了自由梁的一阶垂向弯曲振动频率方程；然后，结合车体结构特征，推导和修正了车体的一阶垂向弯曲振动频率解析方程，并以某地铁车体对解析方程进行了有限元的验证；最后，选取车体的6组设计参数进行了车体一阶垂向弯曲振动频率的灵敏度分析。根据研究结果，给出了车体关键参数对其一阶垂向弯曲振动频率影响程度的排序，为列车车体设计相关工作提供了参考依据。

灵敏度分析；垂向弯曲频率；设计参数；系统响应

0　引言

在新车型开发设计中，如何判断车体结构的设计合理性及车体结构动静态性能的优劣，并针对现存车体结构的不足对其进行优化设计是一项十分重要的工作。当前对车体轻量化要求较高，如何在车体质量与其力学性能之间进行平衡与取舍，以较小的质量代价获得较大程度的力学性能提升，是当前车体结构优化设计工作的重点。

目前获得列车车体模态的方法主要有有限元法和模态试验法[1]两种。有限元法基于车体的三维模型建立有限元模型，并进行求解计算，有限元法能够较准确地得到车体模态，但建立有限元模型需耗费大量的时间；模态试验法则是一种车体性能检验手段，以真实车辆为试验对象，但无法对三维模型阶段的车体进行指导设计。阳光武等[1]基于Timoshenko梁理论并结合车体结构的特点，得到了车体的一阶垂向弯曲频率方程，计算结果通过了有限元和模态试验验证，但模型中未考虑门窗高度对弯曲刚度的影响。王璐等[2]以160 km/h电力机车为研究对象，对其进行灵敏度分析，得到了对车体质量影响大的组件，并进行了二次优化，最终使车体在满足强度与刚度要求的条件下，减重5.25 t，达到了轻量化的目的。郭祥涛[3]着重分析了国产化高速车TC07车车体的18个主要部件对质量、约束等的灵敏程度，找到在满足车体力学性能的条件下对车体质量减轻最敏感的部位，并对其进行了优化。潘婷[4]采用有限元法对CRH3型动车组TC02车进行了模态分析，并以车体15个主要部件为设计变量，对车体进行灵敏度分析，选取对车体模态影响小的结构进行优化设计，最终减重0.42 t。

对车体结构进行灵敏度分析,获得影响车体性能的关键参数，把握车体设计工作重点，能够在车体设计初期对车辆整体参数进行有效的评估，掌控车体优化设计的走向。可见，对于具有诸多设计变量的车体结构来说，灵敏度分析是提取对目标函数影响较大关键参数的非常有效的方法。因此，本文提出一种基于灵敏度分析的车体垂向弯曲刚度优化方法，采用关键参数的相对灵敏度分析，确定关键设计变量对系统响应的影响，得到结构设计变量(车体结构关键参数)对目标约束函数(车体一阶垂向弯曲振动频率)影响的变化梯度。

1　灵敏度分析原理

灵敏度是一个广泛的概念，灵敏度即求导信息，灵敏度分析是一种度量和评价由于设计变量或参数的改变而引起结构响应特性变化率的方法[5]。从数学意义上可以理解为：若函数F(x)可导，其一阶灵敏度可表示为[6]

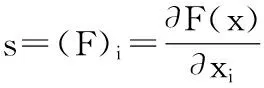
(1)

振动频率对设计变量的灵敏度反映的是设计变量或设计参数的改变对目标函数的影响。由多自由度振动系统的振动方程[3]可得

(K-ω2M)φ=0

(2)

式中，K为刚度矩阵；ω为频率；M为质量矩阵；φ为主振型。

对设计变量xi求偏导，得

(3)

由于K为对称阵，式(3)左乘φT，整理为

(4)

式(4)中,(Kφ-ω2Mφ)T=0，则简化为

(5)

采用振型向量对质量矩阵作归一化处理，即φTMφ=1，则进一步简化为

(6)

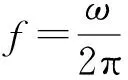
(7)

2　车体垂向弯曲振动频率公式推导

2.1公式的修正

由欧拉-伯努利梁横向振动微分方程，代入初始条件和边界条件，得自由梁的一阶垂向弯曲振动频率方程[7]：

(8)式中，l为自由梁长度；E为弹性模量；I为梁横截面对中心主轴的截面惯性矩；V0为梁的单位体积；A为横截面面积。

由于列车车体并非规则的梁结构，因此需对公式进行如下变形：

(9)

(10)

(11)

应用各截面I计算各段的刚度时，需要将每个截面对于其自身的形心惯性矩利用平行移轴公式[8]移动到车体重心所在位置，如：

I0=Ic+a2A

(12)

式中，I0为通过车体质心的惯性矩；Ic为通过形心的惯性矩；a为形心与质心的距离。

设均质梁平均分为n段，则每段刚度k′相等，为

(13)

梁的串联等效刚度可表示为

(14)

等效后梁的频率为

(15)

由此得到等效后梁的频率为原均质梁频率的n倍，若直接应用等效刚度进行计算，则应在均质梁的频率计算式中应除以分段数n，即

(16)

2.2基于简化车体的频率公式的修正与验证

本文建立了2门4窗、3门4窗和4门3窗三个简单车体模型。以2门4窗车体为例，三维模型如图1所示，分段方法如图2所示，车体基本参数如表1所示。

图1　2门4窗车体模型

图2　模型分段示意图

车长L(mm)车宽b(mm)车高h(mm)车体质量m(t)弹性模量E(MPa)密度ρ(g/mm3)泊松比ν240002500280046.4690002.7×10-30.34

3个车体解析计算结果与有限元结果如表2所示。

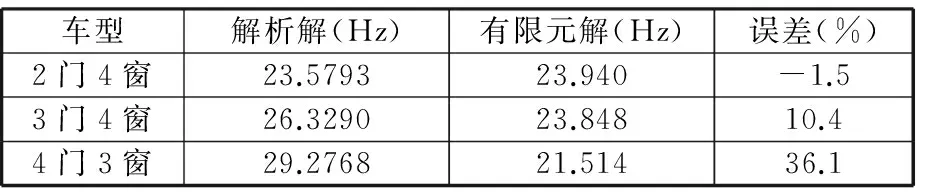
表2　3种车体解析结果与有限元结果

由表2可以看出解析解与有限元解误差不收敛，这是由车体分段不平均导致的，而分段长度的标准差体现了分段的不平均水平，因此引入标准差σ与平均值μ的比值，即变异系数c[9]，对式(16)进行修正。3种车体分段参数如表3所示。

表3　3种车体分段参数

(17)

由式(17)可得0.49

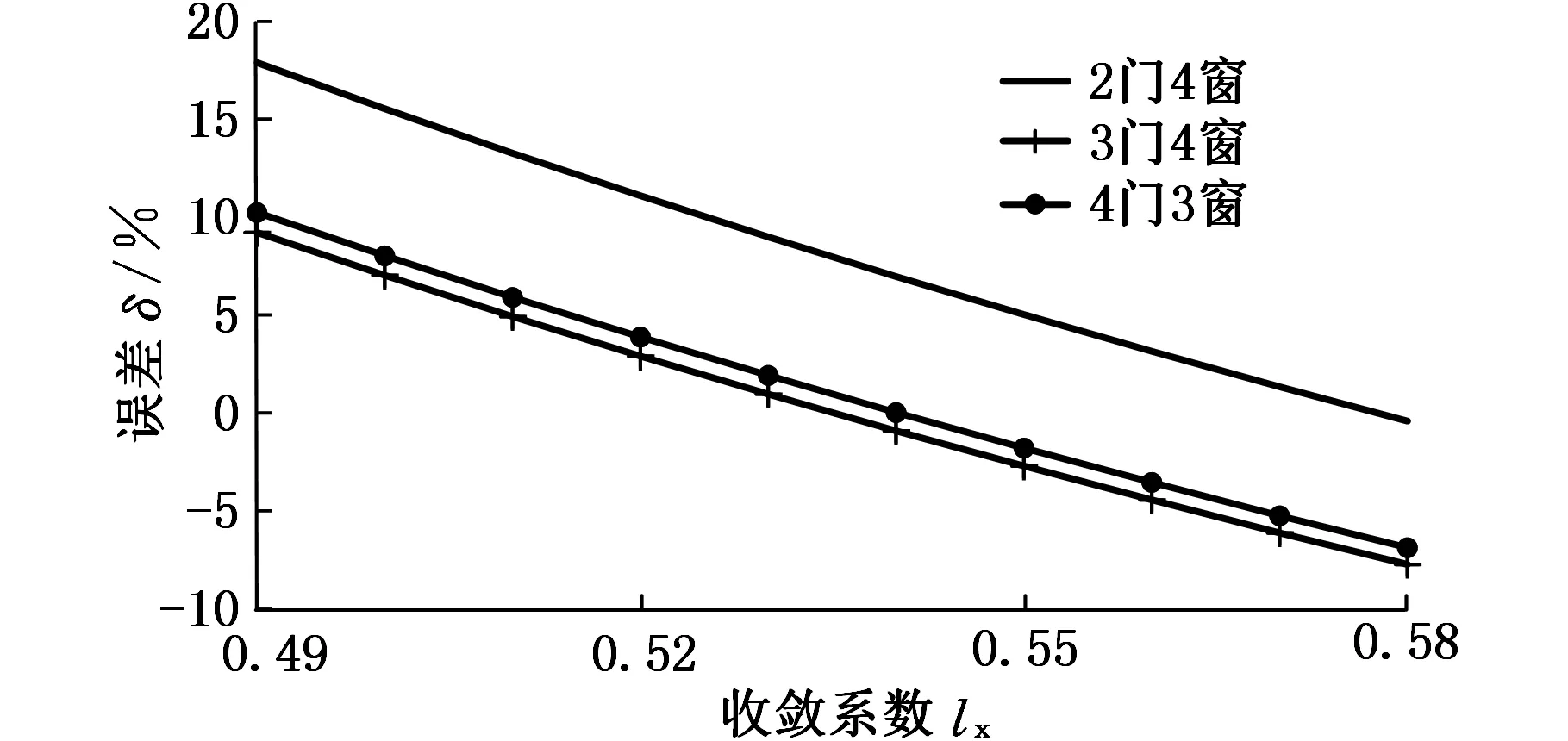
图3　误差变化曲线

由图3知，当收敛系数lx=0.56时，三个车体的垂弯频率误差均在上下5%的限制线以内，修正系数s修正效果最好。且对于不同的车体，分段情况不同，c值不定，则对不同的车体将有不同的修正系数s，是一种动态修正，因此称s为动态修正系数。得最终修正公式：

(18)

该修正方法能够使3种车体的误差均在5%以内，各车体修正结果如表4所示。

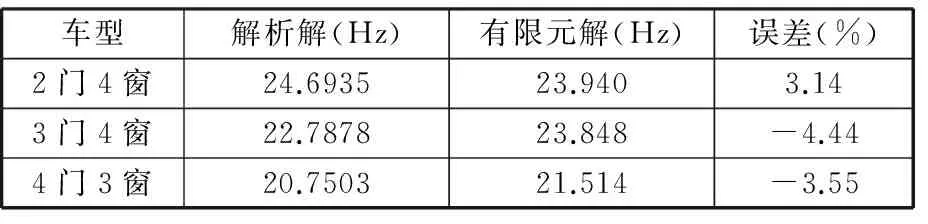
表4　3种车体修正结果

2.3实车验证

以某地铁车为例验证公式的有效性，该地铁车的三维模型及分段方法分别如图4、图5所示。

图4　某地铁车体三维模型

车体的局部特征对振动模态影响很小，可忽略不计，采用整车模型建模，将车体离散为六面体及五面体共1 381 135个实体单元和233 737 3个节点，单元类型为SOLID185，单元大小为30 mm，车体材料的弹性模量为69 GPa，材料密度为2.7×10-3g/mm3，泊松比为0.3。应用ANSYS计算车体的自由模态，得到车体一阶垂向弯曲振动频率为18.05 Hz，计算结果如图6所示。

该解析公式是基于标准欧拉-伯努利梁建立的，并经由实心车体修正完成，而目前绝大多数铝合金车体普遍应用大型中空挤压型材，实现了轻量化，且其抗弯刚度也仅比实心型材略低。因此，应回归到实心车的计算方法中，即在质量计算时，采用车体相同轮廓的实心截面。

图5　某地铁车体分段示意图

图6　某地铁车一阶垂向弯曲振动频率

将24组截面信息等效后代入式(18)，得解析值为18.42 Hz，误差为2%，证明了该计算方法的有效性。

3　车体关键参数的灵敏度分析

对车体的一阶垂向振动频率解析公式的修正过程就是对影响车体垂向振动频率的关键参数的分析过程。为了确定这些关键参数(设计变量)对车体垂向振动频率(目标函数)的影响程度，须对其进行系统的灵敏度分析。

影响车体一阶垂向弯曲振动频率的因素主要有：车体长度、车门宽度、车窗宽度、横截面面积、车体重心垂向高度、车体抗弯刚度等。采用相对灵敏度[10]分析方法对车体的一阶垂向振动频率进行灵敏度分析：

式中，S为相对灵敏度；Δy为因变量的相对变化量；Δx为自变量的相对变化量。

图7　车体垂向振动频率随车体长度变化趋势

以2.3节所示地铁车体的参数为基准，向下调整10%进行灵敏度分析。假设设计变量为a，向下调整10%后为0.9a，则其相对变化量为(a-0.9a)/a=10%。取该地铁车车体长度L参数为例，使其在1倍车长到0.9倍车长范围内变化，频率随车长的变化如图7所示。目标函数值随设计变量的变化及灵敏度如表5所示。

表5　目标函数变化及灵敏度

表5中的相对灵敏度负值表示随着设计变量的减小(或增大)，目标函数值相应增大(或减小)，正值表示随着设计变量的减小(或增大)，目标函数值相应减小(或增大)，数值绝对值的大小表示目标函数对设计变量敏感程度的大小。车体关键参数的灵敏度如图8所示。

图8　车体参数灵敏度

4　结论

本文以基于欧拉-伯努利梁振动方程得到的车体一阶垂向弯曲振动频率修正公式为依据，对某地铁车体进行了车体参数的灵敏度分析，并得到以下结论：

(1)得到了以等效刚度计算的均质梁的垂向振动频率与梁的固有频率的关系，即以串联等效方式得到的梁的频率为原频率的n倍(n为梁的平均分段数)。

(2)对车体一阶垂向弯曲振动频率影响大的参数按影响程度大小排序依次为：车体长度、车体截面面积、车体抗弯刚度、车窗宽度、车门宽度及车体重心垂向高度。其中，车体长度的影响最为明显，车体重心垂向高度的影响最小。

(3)车体轻量化要求以较小的质量代价获得较大程度的力学性能，体现在车体截面上为以较小的截面面积获得较大的抗弯刚度，在断面优化设计中，应注重关键参数的合理匹配，避免经验导向设计，在车体达到减重目的的同时，保证其具有足够的刚度。

[1]阳光武,高一丁,万波. 车体一阶垂向弯曲频率解析分析[J]. 铁道车辆,2015,53(1)：1-6.

YangGuangwu,GaoYiding,WanBo.AnalyticAnalysisoftheFirstOrderVerticalBendingFrequencyofCarbodies[J].RollingStock,2015,53(1):1-6.

[2]王璐,肖守讷,朱涛,等. 160km/h电力机车车体轻量化研究[J]. 机车电传动,2015(3):35-38.

WangLu,XiaoShoune,ZhuTao,etal.ResearchonWeightLighteningof160km/hElectricLocomotiveBody[J].ElectricDriveforLocomotives,2015(3):35-38.

[3]郭祥涛. 高速动车组铝合金车体结构分析及基于灵敏度分析的优化[D].北京：北京交通大学,2011.

[4]潘婷. 动车组车体灵敏度分析及优化设计[D].大连：大连交通大学,2013.

[5]唐明裴,阎贵平. 结构灵敏度分析及计算方法概述[J]. 中国铁道科学,2003,24(1):76-81.

TangMingpei,YanGuiping.OverviewofStructuralSensitivityAnalysisandComputationMethod[J].ChinaRailwayScience,2003,24(1):76-81.

[6]胡浩. 客车车身结构灵敏度分析与拓扑优化[D].武汉：华中科技大学,2006.

[7]高淑英,沈火明.振动力学[M].北京:中国铁道出版社,2011.

[8]单辉祖．材料力学[M]. 北京:高等教育出版社，2000.

[9]钟新联. 统计基础知识[M]. 北京:中国财政经济出版社,1998.

[10]蓝浩伦. 不锈钢地铁车辆车体刚度灵敏度分析[D].大连:大连交通大学,2011.

(编辑袁兴玲)

Sensitivity Analysis about Design Parameters for Car-body Vertical Bending Vibration Frequencies

Wang Changke1Yang Guangwu1Zhu Tao1Yu Jinpeng2

1.State Key Laboratory of Traction Power, Southwest Jiaotong University,Chengdu，6100312.CRRC Tangshan Co., Ltd., Tangshan,Hebei，064000

The sensitivity analysis about key parameters of a car-body was carried out with the stiffness optimization method to find the relationship among design variables and system responses, the gradient of the structure variables (key parameters of car-body) for the target functions (first order vertical bending frequency of car-body) was obtained. First, the first order vertical bending frequency equation was built from Euler-Bernoulli theory with initial and boundary conditions. Then, the frequency equation was corrected with car-body characteristics to get an accurate result, and the results were tested by a finite element result of a subway car-body. Finally, sensitivity analysis was done with 6 key parameters for the bending vibration frequency of car-body. The conclusions show the significance sequence of main car-body parameters for first order vertical bending frequency according to the sensitivity, which may give some advices to designers.

sensitivity analysis; vertical bending frequency; design parameter; system response

2015-11-09

国家科技支撑计划资助项目(2015BAG12B01-15)；四川省科技厅应用基础研究资助项目(2014JY0242)；中央高校基本科研业务费专项资金资助项目(2682015CX046)

U270.2

10.3969/j.issn.1004-132X.2016.16.024

王长科，男，1989年生。西南交通大学牵引动力国家重点实验室硕士研究生。主要研究方向为机车车辆车体强度及振动疲劳。阳光武，男，1977年生。西南交通大学牵引动力国家重点实验室研究员、博士。朱涛，男，1984年生。西南交通大学牵引动力国家重点实验室助理研究员、博士。于金朋，男，1979年生。中车唐山机车车辆有限公司工程师。