凸轮轴数控磨削轮廓误差分析与补偿

杨寿智　邓朝晖　刘　伟　李　建　彭克立

1.湖南大学，长沙，4100822.湖南科技大学难加工材料高效精密加工湖南省重点实验室，湘潭，4112013.湖南海捷精密工业有限公司，长沙，410205



凸轮轴数控磨削轮廓误差分析与补偿

杨寿智1邓朝晖2刘伟2李建1彭克立3

1.湖南大学，长沙，4100822.湖南科技大学难加工材料高效精密加工湖南省重点实验室，湘潭，4112013.湖南海捷精密工业有限公司，长沙，410205

在分析国内外磨削加工误差分析与补偿研究现状基础上，针对X轴和C轴两轴联动的凸轮轴数控磨削的轮廓误差提出一种轮廓误差分析和补偿策略，以提高凸轮磨削加工精度。基于凸轮轴数控磨削的X-C联动运动模型，推导了由凸轮升程表到磨削加工位移表的数学模型；指出凸轮升程与轮廓的误差变化规律在趋势上具有一致性。基于最小二乘多项式方法对多次磨削加工实验的凸轮升程误差进行一系列拟合处理，得到稳定的、可重复的凸轮升程预测误差；将升程预测误差按一定比例反向叠加到理论升程表中，采用最小二乘多项式法进行光顺，得到光顺的虚拟升程表；利用虚拟升程表对同类型凸轮轴进行磨削加工实验。实验结果表明，砂轮架速度和加速度在机床伺服响应范围之内，凸轮最大升程误差与最大相邻误差降低，凸轮轮廓表面粗糙度值满足加工要求，从而证明该误差分析和补偿方法是正确可行的。

凸轮轴；数控磨削；轮廓误差；最小二乘法

0　引言

凸轮轴是汽车发动机结构中的关键零件，其作用是对发动机气缸的进气和排气行程进行有效控制，优化气门的开闭时间和速度，因此需要合理设计凸轮升程来保证特定的凸轮轮廓。同时，凸轮轴的轮廓精度会直接影响发动机的使用性能，进而影响汽车产品的质量[1]。

凸轮的精加工一般采用磨削加工，其轮廓表面为非圆表面，很难达到较高加工精度要求。凸轮加工精度的主要评价指标有轮廓误差、表面粗糙度等，其中运动模型、环境温度、机床机械精度和位置伺服精度，以及其他控制系统精度都会影响凸轮轮廓误差[2]。凸轮轮廓曲面复杂，若仅从提高硬件精度方面来减小误差，成本太高，可以考虑采用软件处理的方式，对凸轮轴磨削加工误差进行分析和补偿，提高加工精度。

常用的轮廓误差补偿方法主要有三类：第一类是合理设置系统运行参数、各轴控制参数，对单项误差影响因素实施补偿，提高轮廓精度[3-4]。该方法仅对单项误差影响因素实施补偿建模，局限性较大，无法体现出凸轮轮廓误差的多因素综合作用结果[5]。第二类是基于多体系统运动学理论，建立机床各个运动部件的数学模型，推导对应的约束方程，从而提高加工精度[6]。该方法仅针对一部分误差影响因素进行补偿建模，且计算量较大，不易推广[7]。第三类是基于轮廓控制的主动误差补偿，即在线调整各种偏心与倾斜等误差[8]。该方法需要改变机床运动部件的结构，增加在线检测装置，并建立检测结果与数控系统之间的实时通信，成本较高。

加工过程中所有误差的信息都会综合反映到工件被加工表面上，且在确定加工条件下加工误差影响规律是基本稳定的[9]。因此可以基于该加工误差来修正加工过程或数控代码，实现误差补偿，提高轮廓精度。范晋伟等[10]以多体系统运动学理论为基础，开发出凸轮精密磨削过程的误差补偿与动态仿真分析软件。陈逢军等[11]利用在位接触式测量系统对实际磨削轮廓曲线进行重构，计算其与目标轮廓之间的法向距离，得到法向残余误差，令砂轮沿着目标轮廓曲线的法矢量方向移动相应的法向残余误差值，从而实现误差补偿磨削。Chen等[12]提出一种数控磨削尺寸误差的智能自学习预补偿方法，该方法仅对超过设定误差极限的位置进行误差补偿操作。焦青松等[13]针对空间端面磨削三轴联动控制，分析了由砂轮位置变化引起的加工误差，提出在实际插补点上减去偏差的误差补偿方法。

本文综合以上各误差补偿方法的优点，针对凸轮轴数控磨削轮廓误差进行了研究，提出一种新的误差分析和补偿方法。

1　凸轮轴数控磨削运动模型

凸轮轮廓型面由多段高次曲线组成，其磨削加工一般采用砂轮架(X轴)和头架(C轴)的两轴联动(X-C联动)来实现凸轮轮廓加工[14]。凸轮轮廓型面一般以升程表的形式表示，并注明对应测头的类型，如尖顶测头、滚子测头或平底测头等，对于滚子测头还须注明滚子半径rg。其中尖顶测头可看作半径无穷小的滚子测头，滚子半径取0 mm；平底测头可看作半径无穷大的滚子测头，滚子半径取106mm。表1所示为某凸轮轴的凸轮采用滚子测头测得的理论升程表(θ-S)，滚子半径为8 mm，最大升程值为98°位置对应的5.1525 mm升程。为实现凸轮轴数控磨削，需要将升程表(θ-S)转化成位移表(X-C)。

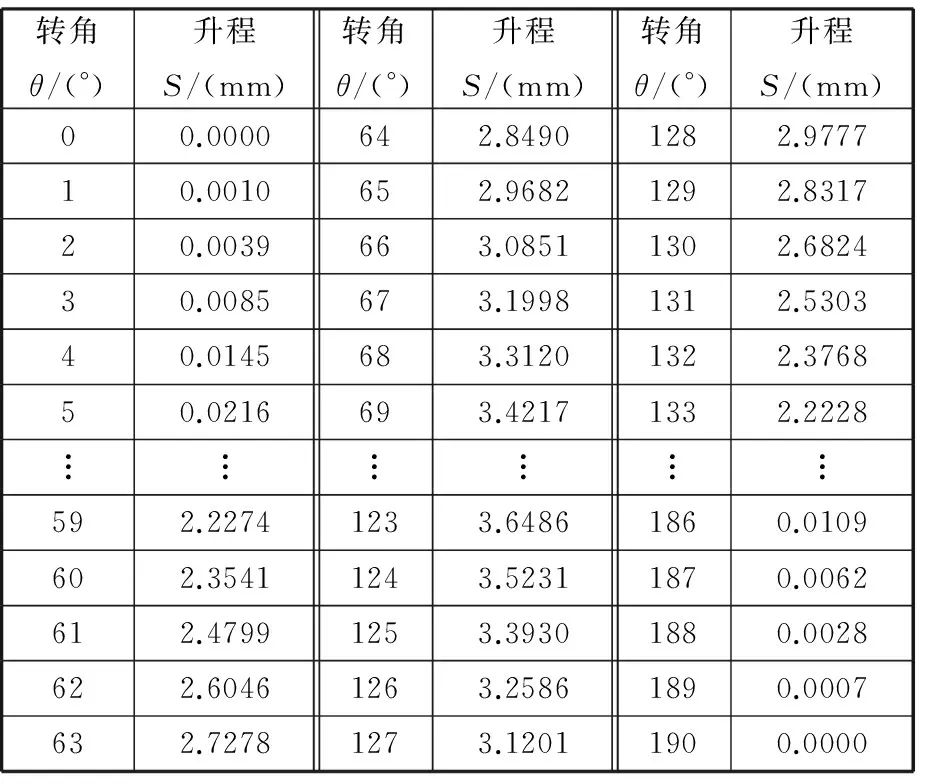
表1　凸轮升程表

图1为凸轮X-C联动磨削示意图，图中，O表示凸轮基圆圆心，rj表示基圆半径，O1表示滚子圆心，rg表示滚子半径，O2表示砂轮圆心，rs表示砂轮半径，B点、C点分别表示凸轮升程的起始点、终止点，α表示凸轮转角，θ表示滚子测头转角。砂轮与凸轮在瞬时磨削点P位置相切，PO2表示过切点的法线，M点表示凸轮和砂轮之间的相对速度瞬心，则升程表(θ-S)转化成位移表(X-C)的计算式如下[14]：

(1)

(2)

|OO1|=rj+rg+S(θ)

(3)

φ=∠OO1M

图1　凸轮X-C联动磨削示意图

由式(1)～式(3)即可求出升程表(θ-S)每一个转角θ所对应的两个量，即砂轮架位移X和凸轮转角α。在实际加工过程中，需要将转化后的位移表X-C进行拟合处理，即在转角α的每一个等分角度点取对应的砂轮架位移X，一般取凸轮每转1°时砂轮架的位移。设定不同滚子半径rg，就可以通过上述方法计算不同测头类型得到的升程表(θ-S)对应的凸轮轴磨削位移表(X-C)。

2　凸轮轴数控磨削轮廓误差分析

凸轮轴数控磨削加工是典型的非外圆磨削加工，各种误差因素综合影响使得X-C联动出现运动不到位的现象，使得实际加工轮廓与理论轮廓存在差异，该差异即为轮廓误差。

对表1所示升程表对应的凸轮轴工件，采用恒线速度磨削数学模型进行多次磨削加工实验，实验后采用BG1310-10型凸轮轴检测仪离线测量凸轮的升程(滚子半径为8 mm)获取实际升程数据表。比较理论升程表与实际升程表，可以得到实际升程误差，如图2、图3所示。需要说明的是：理论升程与实际升程都是每1°转角对应的离散升程值，为便于显示与比较，图2中采用连续曲线表示，后续各图亦同。另外，图2中为便于明显区分理论升程与实际升程两条曲线，将实际升程相对于理论升程的误差放大40倍。

图2　理论升程与实际升程曲线

图3　实际升程误差曲线

为分析凸轮轴数控磨削轮廓误差，需要将凸轮的理论升程表与实际升程表转化成轮廓坐标形式，可采用直角坐标表示。已知凸轮基圆半径rj为15.5 mm，通过下式可以计算凸轮轮廓的直角坐标(x，y)：

(4)

通过式(4)计算得到的理论轮廓和实际轮廓的升程段直角坐标(x，y)中，x的取值不是等间距的，两者的x取值并不对应。为方便比较，将升程段直角坐标(x，y)采用三次样条曲线进行拟合，然后在x向等间距选点得到x取值统一的升程段直角坐标(x，y)，并计算出实际轮廓升程段的y向误差，如图4、图5所示。图4中为便于明显区分理论轮廓与实际轮廓两条曲线，将实际轮廓相对于理论轮廓的y向误差放大100倍。由式(4)可知，图4、图5中曲线最右端位置对应转角0°位置，曲线左端终点位置对应转角190°位置。

图4　理论轮廓与实际轮廓升程段曲线

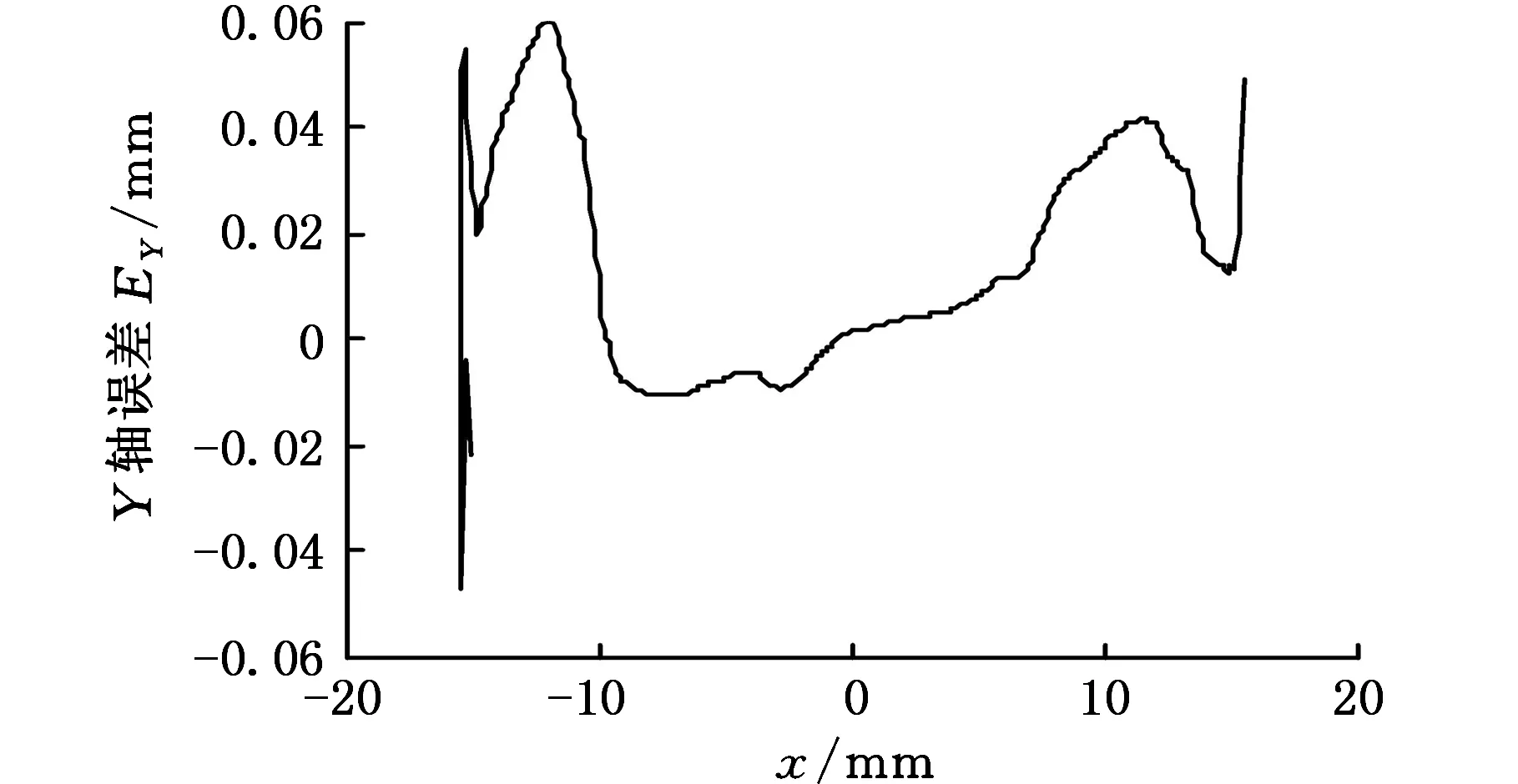
图5　实际轮廓升程段误差曲线

从图2～图5可知，虽然受多种因素的综合影响，凸轮轴实际升程误差在整个磨削过程中出现了较大波动，但是误差值的变化比较明显：

(1)在转角0°～90°位置，凸轮升程误差大于0，实际轮廓相对于理论轮廓向外凸起。在转角13°位置，升程误差有个极小值；过该位置后，误差又逐渐增大，并在转角41°位置达到极大值后开始逐渐减小；最终在转角90°位置两轮廓重合，误差为0。

(2)在转角90°～127°位置，处于凸轮的桃尖部位，凸轮升程误差小于0，实际轮廓相对于理论轮廓是向内凹陷的。过转角90°位置后，凸轮升程误差向负方向逐步增大，在98°的升程最大位置达到负向极大值；而后凸轮升程误差向负方向逐渐减小，在103°位置达到负向极小值；之后，凸轮升程误差继续向负方向逐渐增大，在112°位置误差达到极大值后又开始逐渐减小；最终在转角127°位置两轮廓重合，误差为0。

(3)在转角127°～190°位置，凸轮升程误差大于0，实际轮廓相对于理论轮廓向外凸起。过转角127°位置后，凸轮升程误差逐渐增大，在转角142°位置达到极大值后又开始逐渐减小，并在转角161°位置出现一个极小值，过该位置后升程误差小幅回升后逐渐减小，并回到凸轮轮廓终点所处的转角190°位置。

由此可知，凸轮升程与轮廓的误差变化规律在趋势上具有一致性。为简化计算过程，可直接分析升程误差来代替轮廓误差的变化规律。

图3所示凸轮升程误差曲线中，误差跳动比较大，为找到升程误差的整体变化趋势，对该组误差数据进行拟合处理。为进一步准确拟合升程误差，需要进行以下处理：

(1)误差规律段的选取。在图3所示凸轮升程误差曲线中，一般只有局部某些区域的升程误差值较大，不满足加工要求，因此可以只分析升程误差值比较大的部分(该段升程误差值大于设置误差阈值，且误差呈渐变趋势，逐渐增大或减小)。因此采用逐点判断的方法，记录升程误差值大于设置误差阈值的点数，并通过设置误差曲线分段的最大角度值来选取满足补偿条件的误差规律段。

(2) 全段数据的分段处理。对于凸轮轮廓整体偏胖或者偏瘦的特殊情况，需要对全段进行拟合处理，但是这样常会出现拟合所得曲线无法表达原始数据趋势的现象。在这种情况下，可以将整个凸轮轮廓分为缓冲加速段、顶圆段和缓冲减速段三段进行处理。

采用最小二乘多项式法对各段升程误差进行拟合处理，并综合考虑相邻误差段之间的光顺连接。图3所示凸轮升程误差曲线经拟合处理后得到图6所示曲线，该拟合曲线表示相同工艺条件下的凸轮升程预测误差。

图6　实际升程误差及其拟合误差曲线

3　凸轮轴数控磨削误差补偿

为减小升程误差，提高加工精度，可以将升程预测误差反向叠加到理论升程表中，得到虚拟升程表，用于后续的加工，实现凸轮轴数控磨削轮廓误差的预补偿。

由于加工过程中会存在各种不确定因素的干扰，升程预测误差在拟合过程中也会引入新的误差问题，这些因素使得预测误差本身不可能绝对可靠并稳定，且升程预测误差反向叠加到理论升程表会改变凸轮轴磨削位移表(X-C)，产生一些不可控的问题，因此在误差反向叠加时附加一补偿系数，且将其取值控制在0.8以下。当系统稳定性较好时，可选择较大的补偿系数；当系统稳定性不高时，可选取较小的补偿系数，并通过多次补偿来提高补偿精度。具体计算式如下：

Sx=Sl-kE

(5)

式中，Sx为虚拟升程值；Sl为理论升程值；E为预测误差值；k为补偿系数。

本文中凸轮误差补偿系数k初值取为0.5，计算得到对应的虚拟升程表。虚拟升程曲线可能存在局部几个点或一小段不光顺，在凸轮轴磨削加工过程中会产生轮廓误差，降低轮廓表面质量，因此需要对虚拟升程曲线采用局部光顺法进行光顺处理，同样采用最小二乘多项式法。

光顺后虚拟升程所对应的砂轮架速度和加速度会存在满足机床伺服响应或超出机床伺服响应两种情况。对于满足机床伺服响应而未达到机床最大响应的，可以适当选择较大补偿系数，充分发挥机床的加工能力；对于超出机床伺服响应的，可以适当选择较小补偿系数。本文的凸轮升程经过反复多次调整后，补偿系数k的最优取值确定为0.72，该取值可保证构建的虚拟升程所对应的砂轮架速度和加速度满足机床最大响应。计算得到的虚拟升程曲线如图7所示。其中为便于明显区分各曲线，将实际升程、虚拟升程相对于理论升程的误差都放大40倍，实际升程与虚拟升程总是分布在理论升程的两侧。

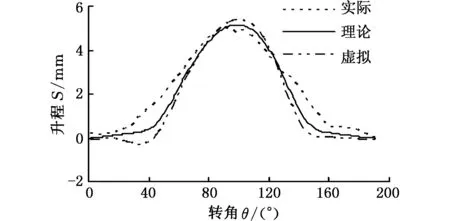
图7　理论升程、实际升程与虚拟升程曲线

4　凸轮轴数控磨削实验验证

凸轮轴磨削实验在CNC8325B高速全数控凸轮轴复合磨床上进行，砂轮采用120号陶瓷结合剂CBN砂轮，砂轮直径为400 mm，磨削液采用水基5%凯牌莫氏浓缩切削液；凸轮轴材料为冷激铸铁，凸轮基圆半径为15.5 mm，升程误差最大允许值为0.020 mm。采用BG1310-10型凸轮轴检测仪检测凸轮升程，采用MarSurf M300便携式粗糙度测量仪测量表面粗糙度。

图8为光顺后虚拟升程所对应的砂轮架速度和加速度曲线，可知砂轮架速度和加速度跳变较小，砂轮架最大速度与最大加速度分别为-137.61 mm/s与1275 mm/s2，在机床伺服响应范围之内[15]。

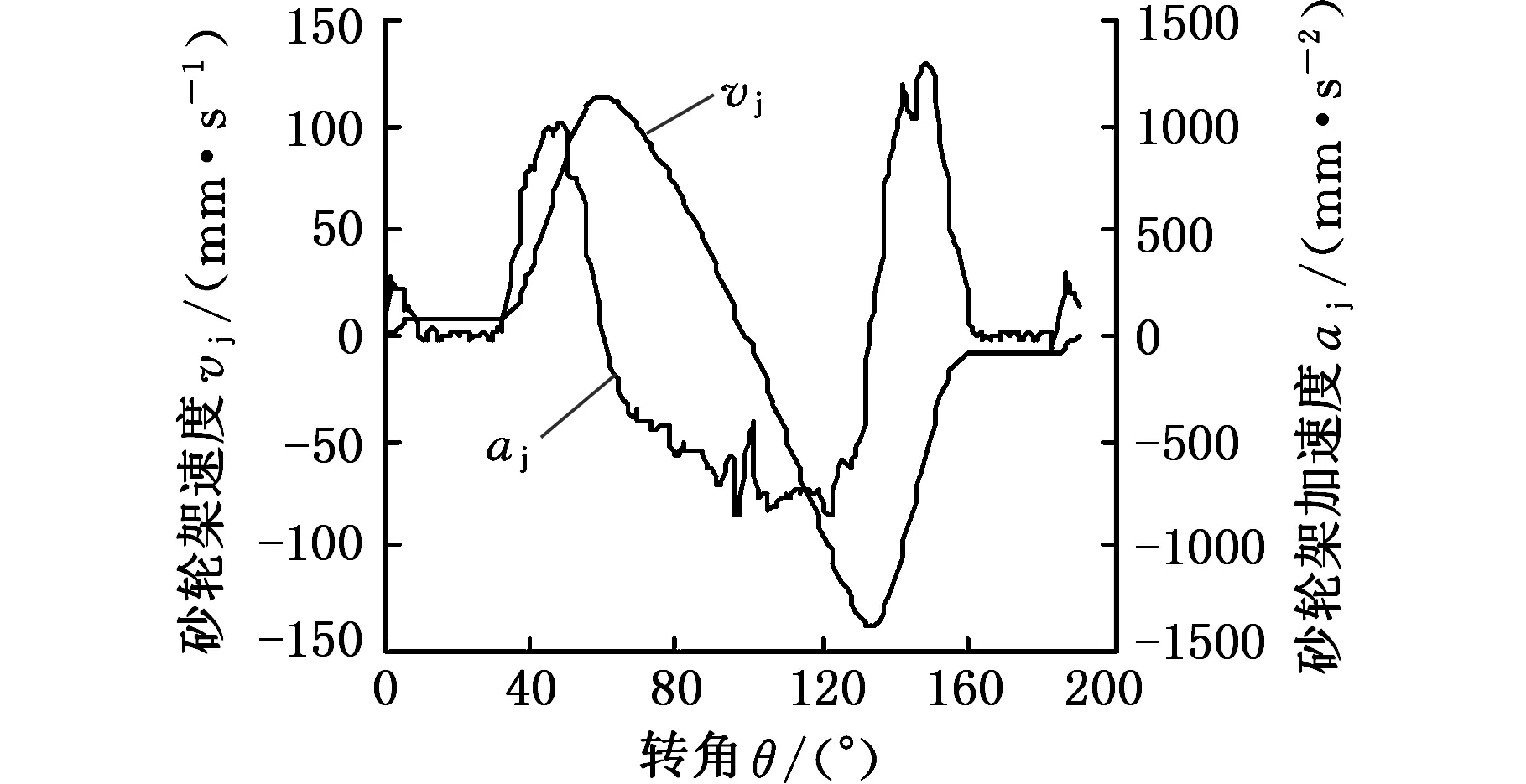
图8　砂轮架速度与加速度曲线

基于误差补偿处理后的虚拟升程表进行凸轮轴磨削加工实验，工艺方案与补偿前一致，测量补偿后的升程与表面粗糙度。补偿前后凸轮升程误差曲线如图9所示，其中实际所对应曲线表示补偿前的误差曲线。由图9可知，补偿前该凸轮片的最大升程误差在转角142°位置处，为0.0262 mm，超过升程误差最大允许值，不符合加工要求。经误差补偿处理后，转角142°位置处误差值降到0.0141 mm，凸轮片的最大升程误差降到0.0173 mm(转角137°位置处)，符合加工要求；同时，补偿前后凸轮的最大相邻误差分别为0.0033 mm、0.0015 mm，得到有效降低。

图9中补偿后的凸轮升程误差在某些转角区域相比补偿前有不同程度的增大，这是因为升程预测误差的反向叠加改变了凸轮原始轮廓尺寸，同时对补偿后的相邻区域位置产生了影响。但是整体而言，补偿后的凸轮升程误差值变小。升程部分轮廓的表面粗糙度值Ra在0.30～0.40 μm之间，满足加工要求。因此该误差分析和补偿方法是正确而且是可行的。

图9　补偿前后凸轮升程误差曲线

5　结论

(1)基于凸轮轴数控磨削的X-C轴联动运动模型，推导了由凸轮升程表(θ-S)到磨削加工位移表(X-C)的数学模型。

(2)分析比较理论与实际升程、理论与实际轮廓，可知升程和轮廓的误差变化规律在趋势上具有一致性。因此基于最小二乘多项式方法对多次磨削加工实验的凸轮升程误差进行一系列拟合处理，可以得到稳定的、可重复的凸轮升程预测误差。

(3)将升程预测误差按一定比例反向叠加到理论升程表中，得到虚拟升程表，采用最小二乘多项式法对虚拟升程进行光顺，实现凸轮轴数控磨削轮廓误差的预补偿。

(4)利用误差补偿处理后的虚拟升程表进行凸轮轴磨削加工实验，由结果可知：砂轮架速度和加速度跳变较小，在机床伺服响应范围之内；凸轮最大升程误差、最大相邻误差与补偿前的相比降低了；凸轮轮廓表面粗糙度满足加工要求。证明该误差分析和补偿方法是正确而且是可行的。

[1]张晓红. 凸轮轴数控磨削工艺智能专家系统的研究及软件开发[D]. 长沙: 湖南大学, 2010.

[2]余顺. 数控凸轮加工成型、质量控制及其机床设计关键理论研究[D]. 武汉: 武汉理工大学, 2006.

[3]LeiWT,HsuYY.AccuracyEnhancementofFive-axisCNCMachinesthroughReal-timeErrorCompensation[J].InternationalJournalofMachineToolsandManufacture, 2003, 43(9): 871-877.

[4]IbarakiS,OtaY.AMachiningTesttoEvaluateGeometricErrorsofFive-axisMachineToolswithItsApplicationtoThermalDeformationTest[J].ProcediaCIRP, 2014, 14: 323-328.

[5]李勇. 影响数控凸轮轴磨削加工精度若干因素的研究[D]. 武汉: 华中科技大学, 2004.

[6]张明伟, 沈兴全. 基于多体系统理论的三轴数控机床误差补偿模型[J]. 机械工程师, 2009 (1): 111-113.

ZhangMingwei,ShenXingquan.TheErrorCompensationModelofThree-axisNumericalControlMachinetoolBasedonMulti-bodySystem[J].MechanicalEngineer, 2009 (1): 111-113.

[7]ChenFJ,YinSH,HuangH,etal.ProfileErrorCompensationinUltra-precisionGrindingofAsphericSurfaceswithOn-machineMeasurement[J].InternationalJournalofMachineToolsandManufacture, 2010, 50(5): 480-486.

[8]MöhringHC,GümmerO,FischerR.ActiveErrorCompensationinContour-controlledGrinding[J].CIRPAnnals—ManufacturingTechnology, 2011, 60(1): 429-432.

[9]ZhangK,YuenA,AltintasY.Pre-compensationofContourErrorsinFive-axisCNCMachineTools[J].InternationalJournalofMachineToolsandManufacture, 2013, 74: 1-11.

[10]范晋伟, 关佳亮, 阎绍泽. 提高精密凸轮磨削精度的几何误差补偿技术[J]. 中国机械工程, 2004, 15(14): 1223-1226.

FanJinwei,GuanJialiang,YanShaoze.TechnologyforEnhancingtheGrindingAccuracyofPrecisionCambyGeometricErrorCompensationMethod[J].ChinaMechanicalEngineering, 2004, 15(14): 1223-1226.

[11]陈逢军, 尹韶辉, 范玉峰, 等. 一种非球面超精密单点磨削与形状误差补偿技术[J]. 机械工程学报, 2010, 46(23): 186-191.

ChenFengjun,YinShaohui,FanYufeng,etal.Ultra-precisionSingle-pointGrindingTechniqueandProfileErrorCompensationMethodforMachiningAsphericMould[J].JournalofMechanicalEngineering, 2010, 46(23): 186-191.

[12]ChenT,TianX.AnIntelligentSelf-learningMethodforDimensionalErrorPre-compensationinCNCGrinding[J].TheInternationalJournalofAdvancedManufacturingTechnology, 2014, 75(9/12): 1349-1356.

[13]焦青松, 李迪, 王世勇, 等. 刀剪三轴端面磨削控制及误差补偿方法研究[J]. 机械工程学报, 2015, 51(7): 206-212.

JiaoQingsong,LiDi,WangShiyong,etal.StudyonControlandErrorCompensationMethodof3-axisSurfaceGrindingforKnifesandScissors[J].JournalofMechanicalEngineering, 2015, 51(7): 206-212.

[14]李建. 凸轮轴数控磨削误差分析和补偿技术研究及软件设计[D]. 长沙: 湖南大学, 2009.

[15]杨寿智, 邓朝晖, 吴桂云, 等. 凸轮轴数控磨削工件主轴转速优化建模与实验研究[J]. 中国机械工程, 2016, 27(5): 652-657.

YangShouzhi,DengZhaohui,WuGuiyun,etal.ModelingandExperimentalResearchonWorkpieceSpindleSpeedOptimizationinCamshaftCNCGrinding[J].ChinaMechanicalEngineering, 2016, 27(5): 652-657.

(编辑卢湘帆)

ContourErrorAnalysisandCompensationforCamshaftCNCGrinding

YangShouzhi1DengZhaohui2LiuWei2LiJian1PengKeli3

1.HunanUniversity,Changsha,410082 2.HunanProvincialKeyLaboratoryofHighEfficiencyandPrecisionMachiningofDifficult-to-cutMaterial,HunanUniversityofScienceandTechnology,Xiangtan,Hunan,411201 3.HunanHicamPrecisionIndustryCo.,Ltd.,Changsha,410205

Basedonthecurrentsituationsofgrindingerroranalysisandcompensation,anewcontourerroranalysisandcompensationmethodwasproposedforcamshaftCNCgrindinginX-Caxislinkage,toimprovetheaccuracyofcamgrinding.AccordingtothecamshaftgrindingmotionmodelinX-Caxislinkage,themathematicalmodelwasderivedforcamliftingtogrindingoffset.Itpointedoutthatthevariationtrendsofcamliftingerrorsandcontourerrorswerebasicallythesame.Thenastableandrepeatablecamliftingerrorscouldbepredictedwithseriesfittingofcamliftingerrorsfrommultiplegrindingexperiments,usingleastsquaremethod.Byinversesuperpositionofpredictedliftingerrorstotheoreticalliftingtableinacertainproportion,thevirtualliftingtablecouldbeobtainedafterthesmoothingusingleastsquaremethod.Finally,thecamshaftgrindingexperimentswereappliedaccordingtothevirtualtable.Theexperimentalresultsindicatedthat:thespeedandaccelerationofgrindingcarriagearebasicallyintheresponserangeofgrinderservo,themaximumcamliftingerrorandthemaximumadjacenterroraredecreased,thesurfaceroughnesssatisfieswiththeprocessingrequirements.Itisprovedthattheerroranalysisandcompensationmethodsarecorrectandfeasible.

camshaft;CNCgrinding;contourerror;leastsquaremethod

2016-05-03

国家科技支撑计划资助项目(2015BAF23B01)；国家自然科学基金资助项目(51175163)；高等学校博士学科点专项科研基金资助项目(20110161110032)

TG580

10.3969/j.issn.1004-132X.2016.16.018

杨寿智，男，1972年生。湖南大学机械与运载工程学院博士研究生。研究方向为高效精密智能磨削技术。发表论文近10篇。邓朝晖(通信作者)，男，1968年生。湖南科技大学机电工程学院教授、博士研究生导师，湖南大学机械与运载工程学院教授、博士研究生导师。刘伟，男，1986年生。湖南科技大学机电工程学院讲师、博士。李建，男，1984年生。湖南大学机械与运载工程学院硕士。彭克立，男，1976年生。湖南海捷精密工业有限公司副总经理、高级工程师。