自适应无参经验小波变换及其在转子故障诊断中的应用

郑近德　潘海洋　潘紫微　罗洁思

1.安徽工业大学,马鞍山，243032　　2.厦门理工学院，厦门，361024



自适应无参经验小波变换及其在转子故障诊断中的应用

郑近德1潘海洋1潘紫微1罗洁思2

1.安徽工业大学,马鞍山，2430322.厦门理工学院，厦门，361024

为了实现经验小波变换中Fourier谱的自适应分割，提出了自适应无参经验小波变换(APEWT)方法。同时，为了克服希尔伯特变换解调的不足，更精确地估计信号的时频分布，提出了改进归一化希尔伯特变换(INHT)。通过分析仿真信号将APEWT和INHT方法与经验模态分解(EMD)、总体平均经验模态分解(EEMD)和局部特征尺度分解等方法进行对比，结果表明了APEWT和INHT方法的优越性。最后，将基于APEWT和INHT的时频分析方法应用于转子局部碰磨故障诊断，试验数据分析结果表明，所提出的方法不仅能够有效地诊断转子局部碰磨故障，而且诊断效果优于EMD和EEMD方法。

转子故障；碰磨；经验模态分解；希尔伯特变换

0　引言

时频分析由于能够同时提供信号的时域和频域局部信息而在机械故障诊断领域得到了广泛的应用[1]。机械故障诊断中常用的时频分析方法主要有Wigner-Ville分布、小波变换、经验模态分解(empiricalmodedecomposition,EMD)[1-3]，以及在EMD基础上发展的局部均值分解(localmeandecomposition，LMD)和局部特征尺度分解(localcharacteristic-scaledecomposition，LCD)等[4-7]。来五星等[8]将Wigner-Ville时频分布应用于齿轮故障诊断；Yan等[9]对小波分析在旋转机械故障诊断中的应用进行了总结，并对小波变换在故障诊断的应用前景进行了预测；于德介等[10]将EMD引入到机械故障诊断领域，并对其存在的问题进行了改进和完善；雷亚国[11]研究了基于总体平均经验模态分解(ensembleempiricalmodedecomposition，EEMD)改进的希尔伯特-黄变换(Hilbert-Huangtransform,HHT)在机械故障诊断中的应用。然而，这些时频分析方法都有各自的固有缺陷[12]。

最近，在小波变换的基础上，Gilles等[13-14]提出了一种新的非平稳信号分析方法——经验小波变换(empiricalwavelettransform，EWT)。EWT通过对Fourier谱进行分割，在每个分割的区间建立小波正交基，从而能够将一个多分量信号分解为若干个具有紧支集频谱的调幅调频信号之和。但是，EWT方法的一个关键问题是Fourier谱的分割。为了实现Fourier谱的自适应分割，笔者提出了一种新的非平稳信号分解方法——自适应无参经验小波变换(adaptiveparameterlessEWT，APEWT)方法。

采用APEWT对多分量信号进行分解，得到若干个单分量信号，再对每个单分量信号进行解调即可得到原始信号的完整时频分布。为了更精确地估计信号的时频分布，本文提出一种改进的归一化希尔伯特变换(improvednormalizedHilberttransform,INHT)方法。INHT方法避开了希尔伯特变换(Hilberttransform，HT)方法构造解析信号，瞬时特征的估计精度更高。

1　自适应无参经验小波变换

本文提出的APEWT方法主要包含两部分：Fourier谱的自适应分割和滤波器组的建立。APEWT的关键是对原始信号的Fourier谱进行自适应分割。文献[15]提出将Fourier谱转化成尺度空间表示(函数的尺度空间表示参见文献[16])，将Fourier谱的自适应分割问题转化为如何在尺度空间表示中找到“有意义”模态，并将此问题转化为一个二类聚类问题。

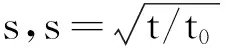
(1)

(2)

为方便，假设τn与ωn成正比，即τn=γωn，0<γ<1。β(x)是一任意区间[0,1]连续的任意函数，依据Meyer小波，选择β(x)=x4(35-84x+70x2-20x3)。

然后，采用类似经典的小波变换方法，通过对信号和经验小波作内积运算的方式得到经验小波变换系数，通过对信号和尺度函数作内积运算得到逼近系数，进而得到原始信号的各阶模态。

本质上，对任意一个复杂的多分量信号，APEWT建立一组自适应的带通滤波器，通过对信号进行带通滤波的方式将其分解为若干个具有紧支集频谱的单分量信号之和，再对得到的单分量信号进行解调，即可得到原始信号完整的时频分布。

2　改进的归一化希尔伯特变换

HT是一种常用且有效的信号解调方法。但由于Bedrosian定理的限制，HT会出现无法解释的负频率。为了克服此问题，文献[18]提出了归一化HT(normalized Hilbert transform，NHT)，NHT首先对EMD分解得到的内禀模态函数(intrinsic mode function，IMF)进行归一化，再对归一化后的IMF作HT。NHT的对象是归一化IMF，不再受Bedrosian定理的限制，但由于受Nuttall定理的局限，跟真实频率之间仍有一定的误差，而且HT和NHT都有严重的端点效应。

为了克服HT和NHT方法的缺陷，本文提出了改进的NHT方法——INHT方法。NHT和INHT都是基于经验调幅调频分解(empirical AM-FM demodulation，EAD)[12，18]方法而提出的，EAD方法能够将一个单分量信号(如IMF)分解为调幅部分和调频部分的乘积，调幅部分即为单分量信号的瞬时幅值。

INHT的具体步骤如下：

(1)对于单分量信号c(t)，首先可采用EAD将其写作调幅部分和调频部分的乘积，即：c(t)=a(t)c1(t)，其中，a(t)是c(t)的瞬时幅值，c1(t)是归一化信号，幅值为1。

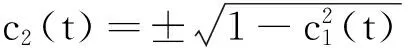
3　仿真信号分析

令仿真信号

s(t)=s1(t)+s2(t)+s3(t)+s4(t)

(3)

t∈[0,1]

其中，s1(t)是频率为200 Hz的载波被频率为指数函数调制构成的调幅调频信号，s2(t)=(1+0.3cos(2π(5t))sin(2π(80t)+2π(5t2))，s3(t)=2(t2+1)cos(2π(40t))，s4(t)=2t2。各个分量的时域波形如图1中虚线所示。

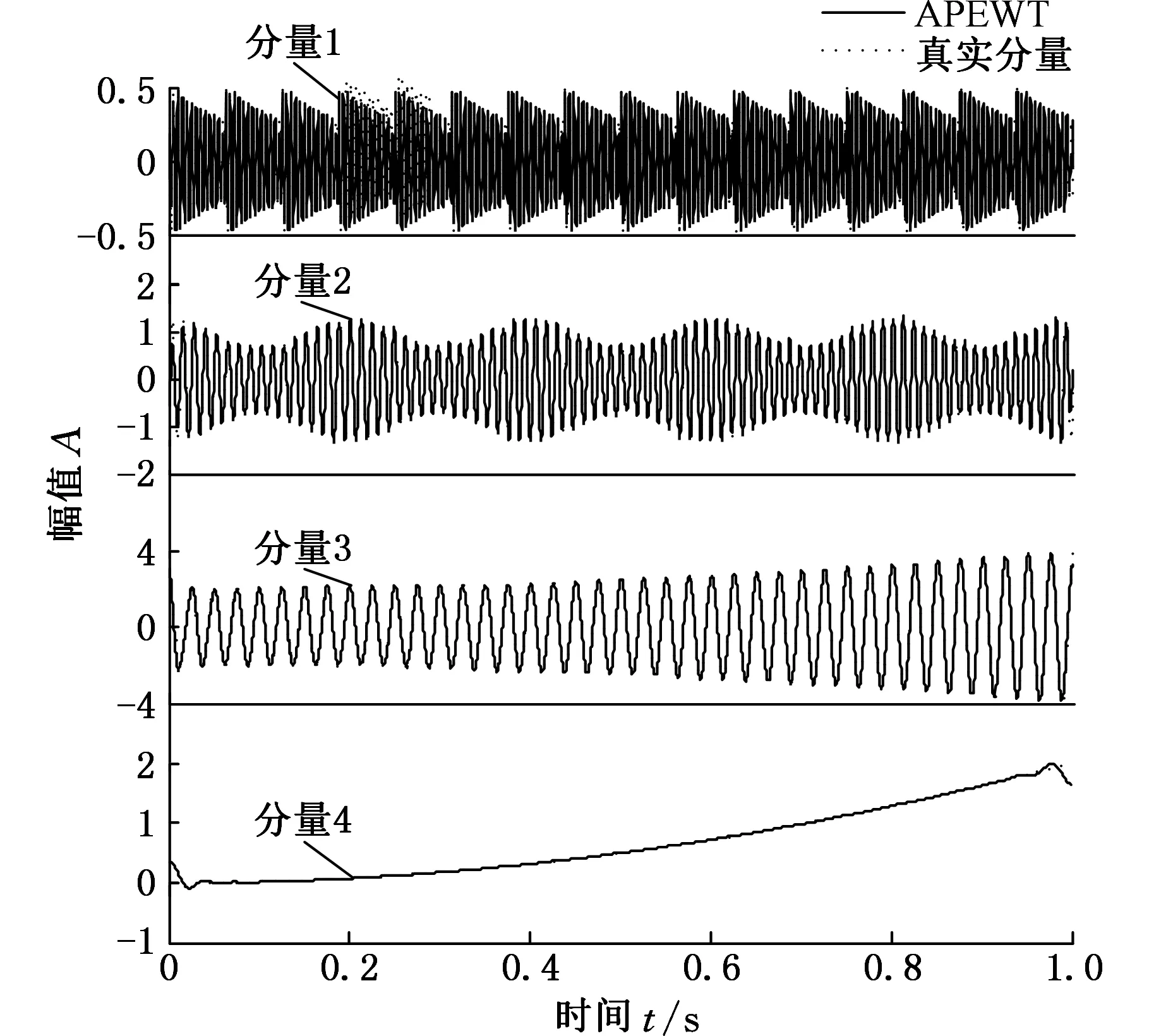
图1　仿真信号s(t)的各个成分及APEWT分解结果

采用APEWT方法对s(t)进行分解，结果如图1中实线所示，其中Fourier谱的分割中采用基于K均值聚类的尺度空间法。通过与真实分量(虚线)对比可以发现，APEWT方法得到的四个分量C1、C2、C3、C4分别对应真实分量s1、s2、s3、s4，对应的实线和虚线几乎重合，它们对应的相关系数分别为0.9929、0.9935、0.9987和0.9973，因此，APEWT方法得到的分量与真实分量的相关性和吻合度很高，分解效果比较理想。

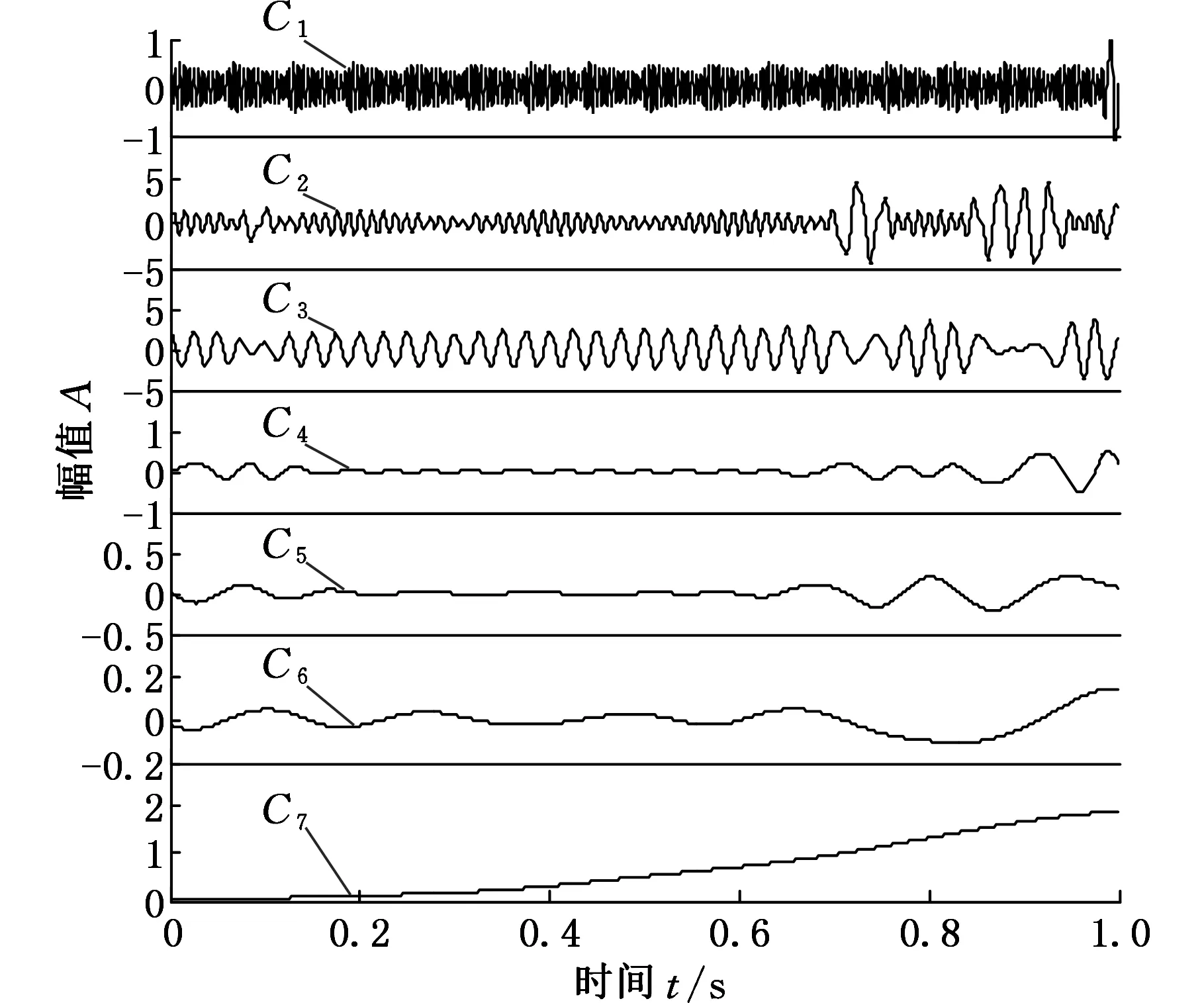
图2　仿真信号s(t)的EMD分解结果

为了对比，再分别采用EMD、EEMD[17]和最近提出的LCD[6,12]对s(t)进行分解。其中，EMD方法的分解结果如图2所示。为节约篇幅，EEMD和LCD方法的分解未给出，下文将给出它们的时频谱。由图2可以看出，EMD的分解结果发生了严重的模态混叠，而且C4、C5、C6为拟合产生的虚假分量。对应的前三个分量和剩余趋势项与对应真实分量s1、s2、s3、s4的相关系数分别为0.9275、0.5408、0.8358和0.9990，分解结果不如APEWT的结果理想。EEMD由于添加的白噪声并不能完全抵消会产生高频的噪声分量，而且仍出现了一个模态被分解为相邻的几个IMF分量的情况；LCD也产生了较多的虚假分量，而且分解的分量与真实分量的吻合度较低。因此，APEWT方法得到的分量与真实分量的吻合度和相似性最高，分解效果最为理想。

采用APEWT方法对原始信号进行分解，得到若干个瞬时频率具有物理意义的单分量信号，再对它们进行解调即可得到原始信号的时频分布。

分别采用HT、NHT、INHT1和INHT2四种方法估计单分量信号s2(t)和s3(t)的瞬时频率，结果如图3所示，其绝对误差分别如图4所示。由图3可知，四种方法估计的s2(t)的瞬时频率都比较精确，差别很小。但由图4的绝对误差中可以看出，HT和NHT方法估计结果有明显的端点效应；而INHT2估计的结果与真实值非常接近，绝对误差水平非常小，结果比较理想。对于s3(t)，分别采用四种方法估计的瞬时频率中，HT端点效应严重，且由两端向中间传播，导致估计值波动较大；而NHT方法的端点效应较小，但仍存在；INHT1克服了二者的端点效应，估计结果比较精确，但估计值比真实值偏小；INHT2方法不仅克服了HT和NHT方法的端点效应，而且绝对误差也非常小，和真实值非常吻合。综上分析，本文提出的估计瞬时频率的INHT方法克服了HT方法的端点效应，估计值更加精确，尤其是INHT2方法，估计效果要优于其他方法。最后，为了对比，分别采用EMD-HT，EEMD-NHT，LCD-INHT1和APEWT-INHT2四种方法估计信号s(t)的时频谱，结果分别如图5a～图5d所示。由图5可以看出，图5a中EMD方法分解得到的伪分量较多，HT方法有明显的端点效应，而且出现了负频率；图5b中EEMD方法得到的分量较多，仍存在模态混叠现象；LCD-INHT1方法中，LCD分解得到的分量也较多；而本文提出的APEWT-INHT2方法得到的时频谱最接近原信号的理想时频谱。因此，上述分析表明了基于APEWT和INHT2的时频分析方法的优越性。

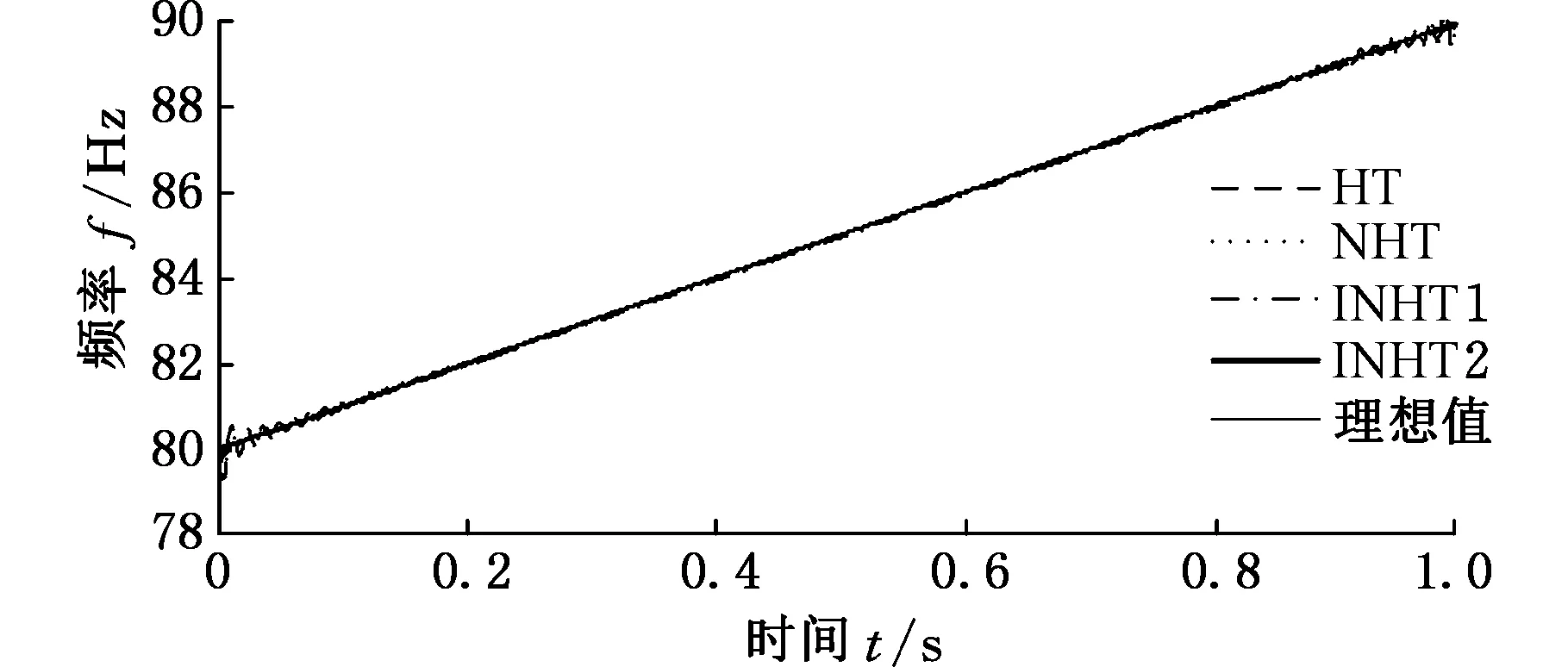
(a) 不同方法估计的s2(t)的瞬时频率

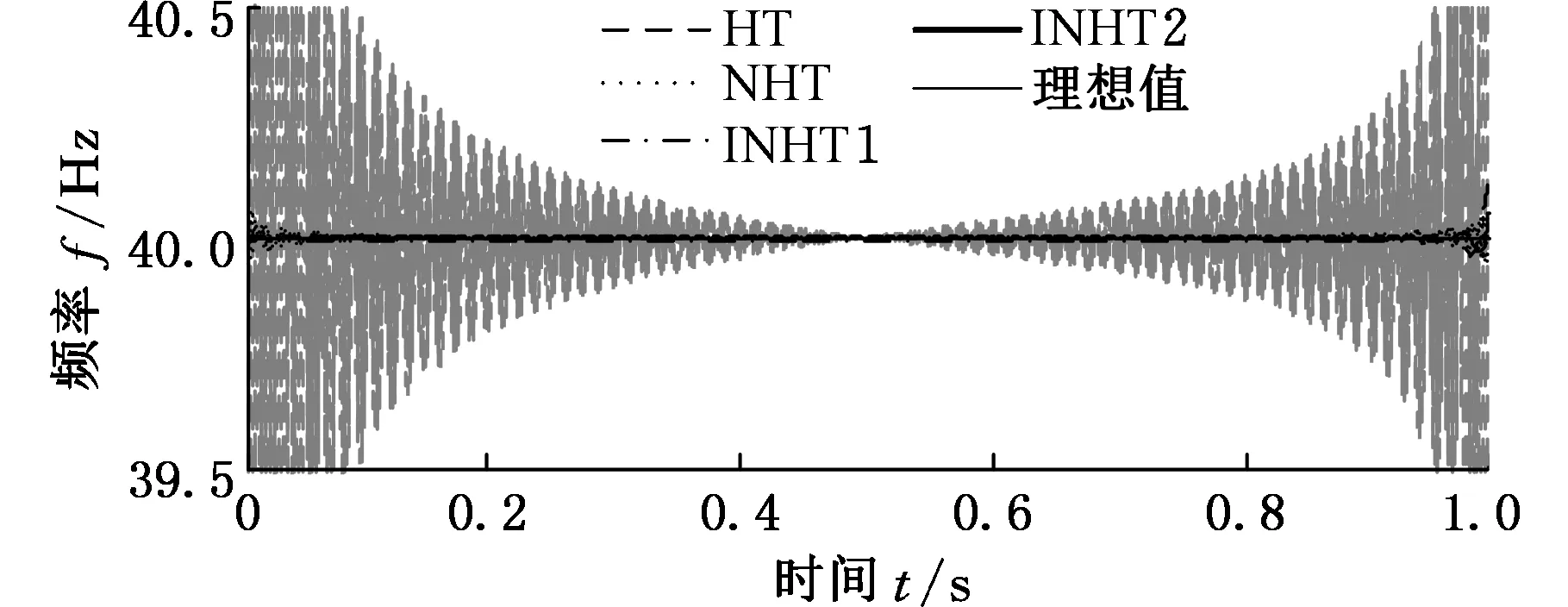
(b)不同方法估计的s3(t)的瞬时频率图3　四种不同方法估计的s2(t)和s3(t)的瞬时频率

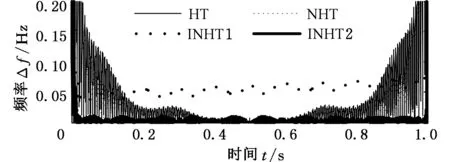
(a) 不同方法估计的s2(t)的瞬时频率的绝对误差

(b)不同方法估计的s3(t)的瞬时频率的绝对误差图4　四种不同方法估计的s2(t)和s3(t)的瞬时频率绝对误差

(a)EMD-HT时频谱　　(b)EEMD-NHT时频谱

(c)LCD-INHT 1时频谱　(d)APEWT-INHT 2时频谱图5　四种不同方法得到的信号s(t)的时频谱

4　实测信号分析

局部碰磨是转子系统常见的非线性振动故障，当转子发生局部碰磨时，转子在旋转的过程中动静件会周期性地发生摩擦，其碰磨信号往往表现为调幅特征，由于具有调幅特征的碰磨信号非常微弱，因此，如何从信号中提取包含故障特征信息的调幅信号是转子局部碰磨故障诊断的关键[19]。

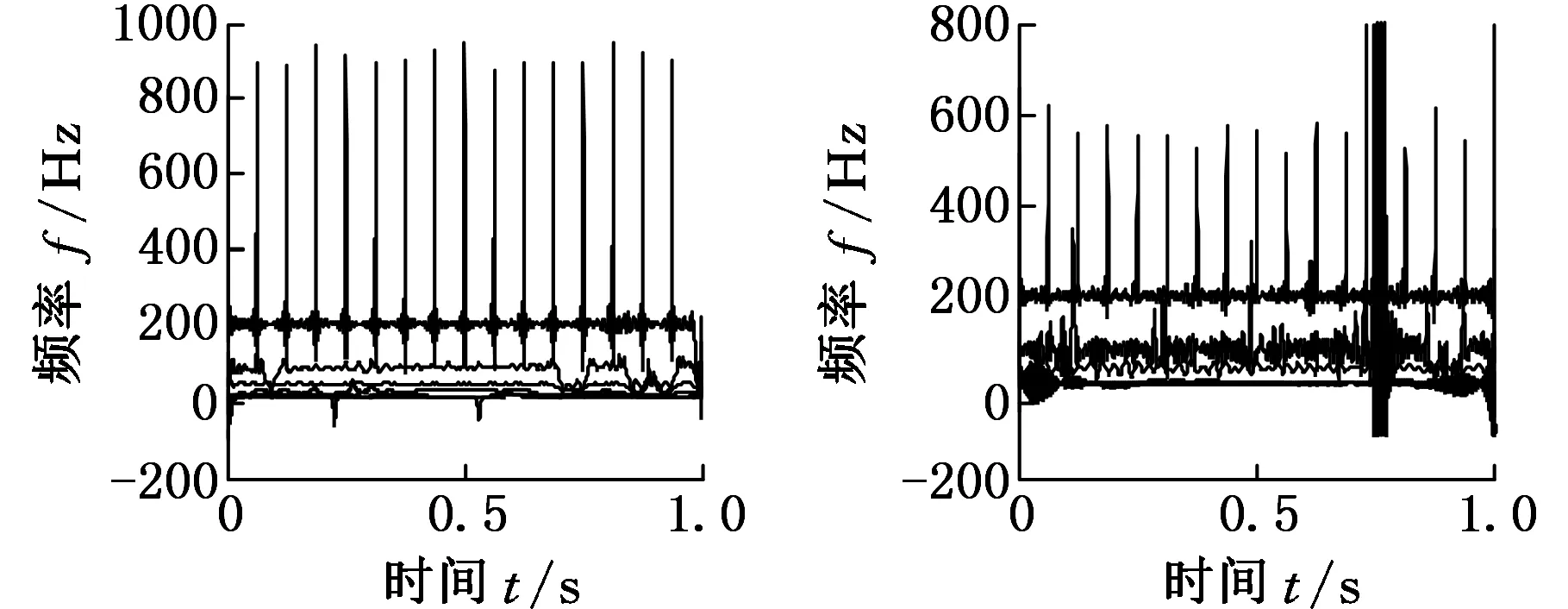
为了验证APEWT和INHT方法的有效性，将其应用于转子动静碰磨故障实验数据的分析。采用Z-T3型转子振动模拟实验台进行转子系统故障实验，实验装置参见文献[19]。在采样频率为2048Hz、转频为50Hz条件下，采集到存在局部碰磨故障的转子径向位移信号，其时域波形及频谱如图6所示，由时域波形和频谱仅能看出工频，而与故障有关的碰磨特征被背景信号和噪声淹没。

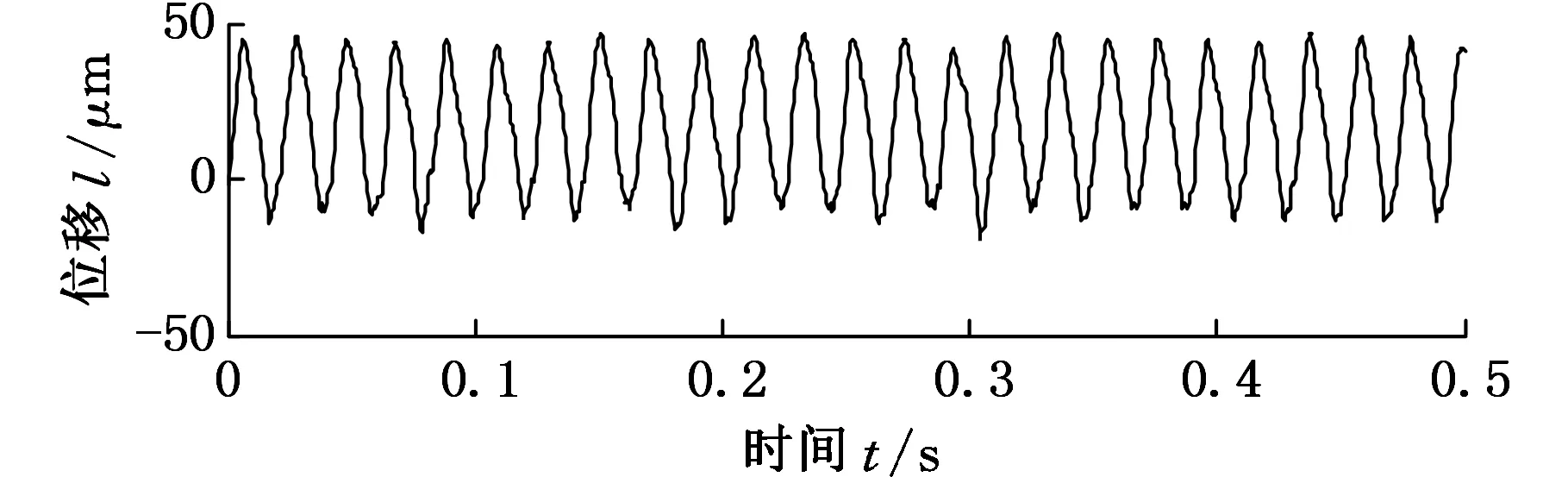
(a)转子位移信号

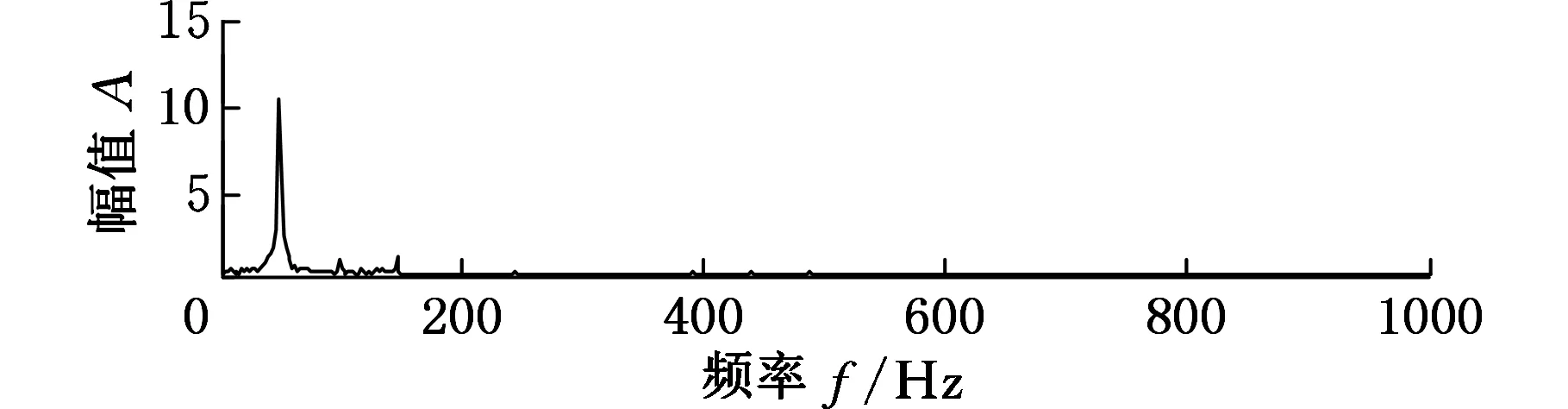
(b)转子位移信号的频谱图6　存在局部碰磨故障的转子位移信号与频谱

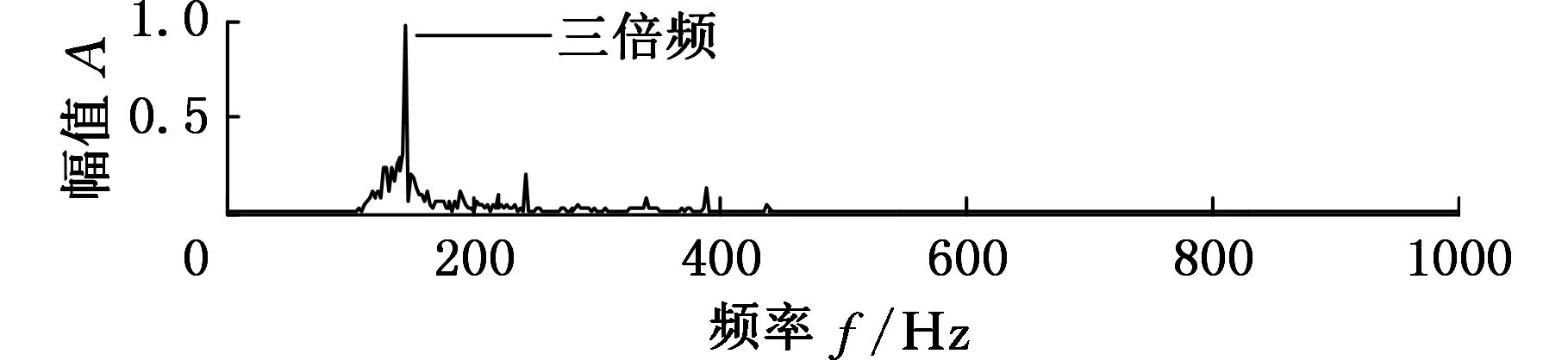
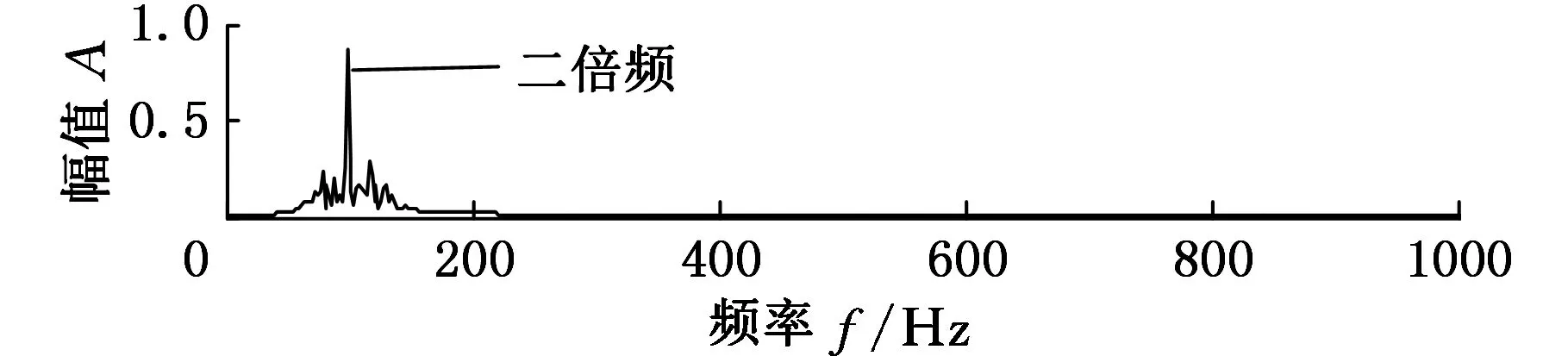
采用APEWT对存在故障的转子径向位移信号进行分解，结果如图7所示。第一个分量的包络谱和第二、三、四个分量的频谱分别如图8所示。综合两图可以看出，第一个分量出现了高频成分的频率调制现象，具有明显的调幅特征，由其包络谱可以看出，调幅的频率为50Hz，刚好等于工频，这是由于转子每转动一周，动静件就碰磨一次造成的。第二、三、四个分量分别为工频的三倍频、二倍频和一倍频，而且，高频谐波分量(三倍频、二倍频)的幅值较大，说明碰磨的程度较重[20]。因此，通过对转子局部碰磨信号进行APEWT分解，将碰磨信号、背景信号和噪声分离，可将高频碰磨信号从强大的背景信号中提取出来。上述分析表明，APEWT方法能够有效地提取转子碰磨故障特征信息。

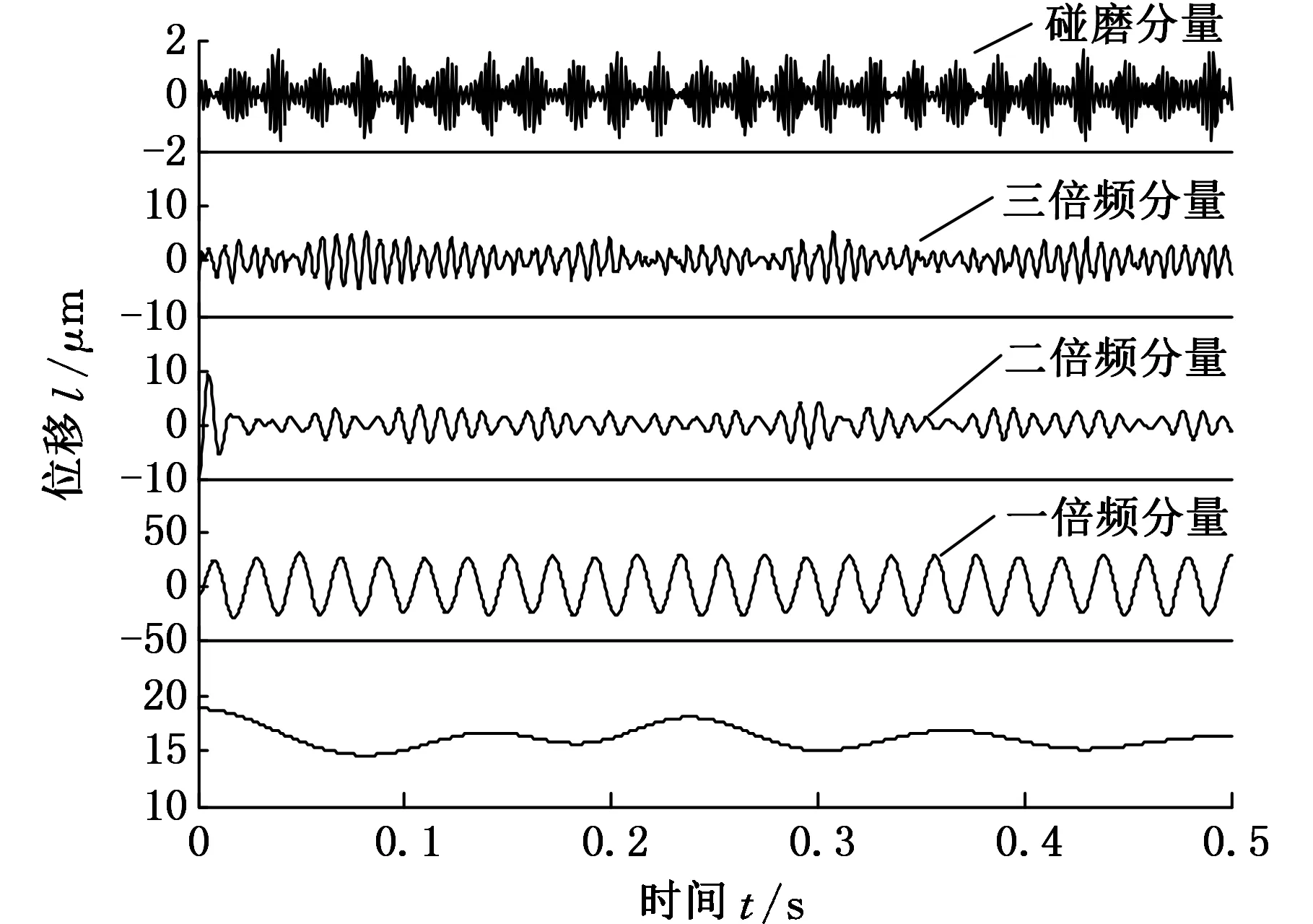
图7　存在局部碰磨故障转子位移信号的APEWT分解结果

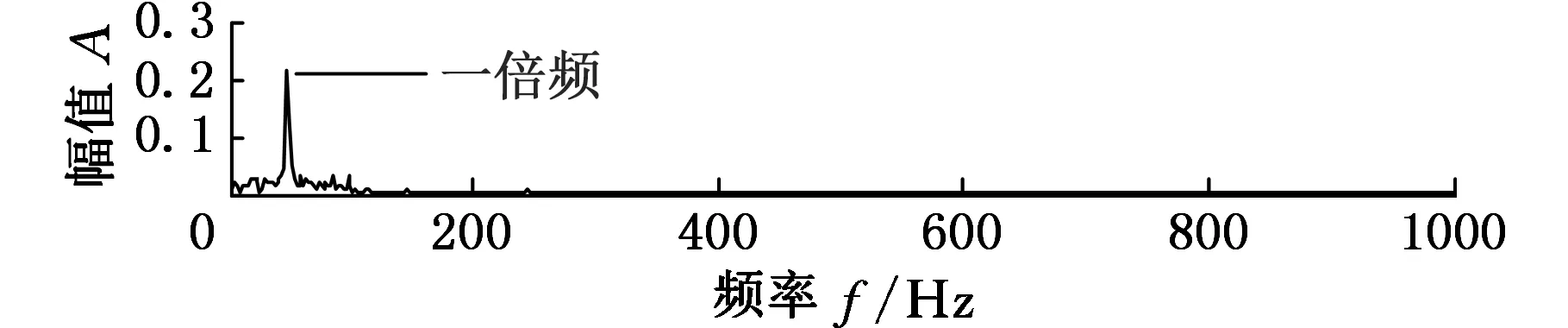
(a)第一个分量的包络谱

(b)第二个分量的频谱

(c)第三个分量的频谱

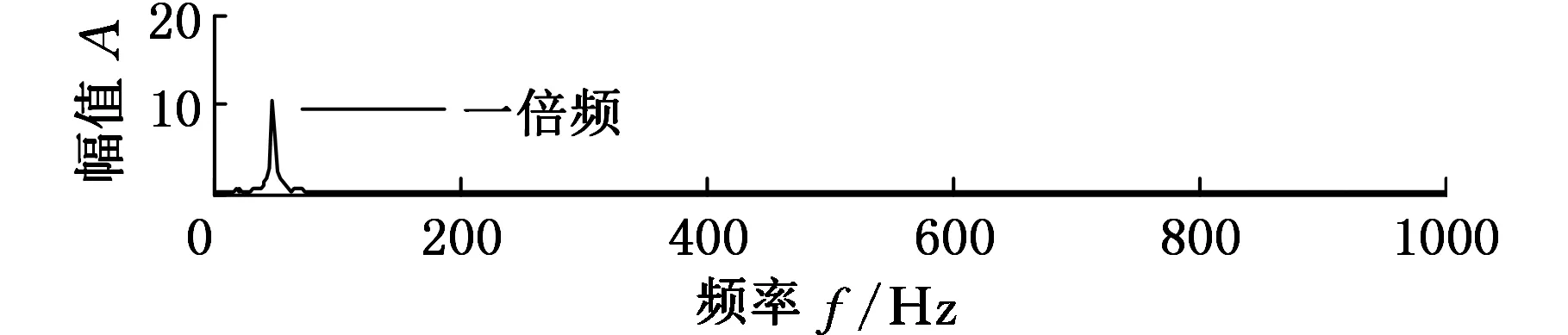
(d)第四个分量的频谱图8　APEWT分解第一个分量的包络谱和其他分量的频谱

为了对比，采用EMD方法对上述存在碰磨故障的转子径向位移信号进行分解，结果如图9所示。由图9可以看出，EMD第一个分量虽然具有调幅特征，但是局部发生了模态混叠，第一个分量的调制频率不仅有转频及其二倍频，而且还包含有低频调制，对故障诊断造成干扰，而且EMD还无法分解出二倍转频和三倍转频信息。再采用EEMD方法对上述转子径向位移信号进行分解，前四个IMF分量和其对应的残余分量结果如图10所示，其中添加噪声的标准差大小为0.15，总体平均次数为100。由图10可以看出，虽然EEMD能够得到具有调幅特征的碰磨信号，但无法分解出二倍转频和三倍转频，第二个分量仍是一个多分量信号，物理意义不明确。因此，APEWT的诊断效果要优于EMD和EEMD方法。

图9　存在局部碰磨故障转子位移信号的EMD分解结果

图10　存在局部碰磨故障转子位移信号的EEMD分解结果

图11为正常转子径向位移信号(图中第一条曲线)及其APEWT分解，结果(图中第2～6条曲线)所示。第一个分量的包络谱和频谱如图12所示。综合两图可以看出，正常转子位移信号的第一个分量的调幅特征不明显，通过其频谱发现，第一个分量为工频的四倍频，而第二、三、四个分量分别为工频的三倍频、二倍频和一倍频，没有明显碰磨故障特征信息，与存在碰磨故障的信号分析结果区别明显。

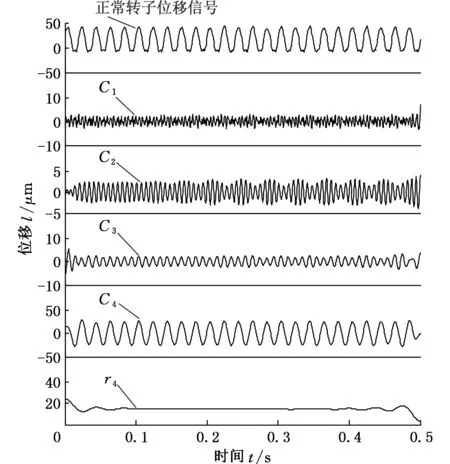
图11　正常转子位移信号及其APEWT分解结果

(a) 第一个分量的包络谱

(b)第一个分量的频谱图12　正常转子信号APEWT分解的第一个分量的包络谱和频谱

5　结论

(1)提出了一种自适应无参经验小波变换(APEWT)方法，通过仿真试验信号将其与EMD、LCD和EEMD等方法进行了对比，结果表明，APEWT方法得到的分量更精确。

(2)针对希尔伯特变换等现有解调方法的不足，提出一种新的瞬时频率估计方法——改进的归一化希尔伯特变换。将其与希尔伯特变换和归一化希尔伯特变换进行了对比，结果表明了本文提出的方法端点效应更小，精确性更高。

(3)将提出的基于APEWT和INHT的时频分析方法应用于正常转子和转子局部碰磨故障的信号分析，通过与EMD和EEMD等方法进行对比，结果表明APEWT方法不仅能有效地诊断转子局部碰磨故障，而且诊断效果优于EMD和EEMD等方法。

APEWT方法也有不足之处，如分解结果依赖于频谱的划分，也存在轻微的端点效应，笔者正针对这些问题展开进一步研究。

[1]何正嘉, 訾艳阳, 孟庆丰, 等. 机械设备非平稳信号的故障诊断原理及应用[M]. 北京: 高等教育出版社, 2001.

[2]吴强, 孔凡让, 何清波,等. 基于小波变换和ICA的滚动轴承早期故障诊断[J]. 中国机械工程, 2012, 23(7): 835-840.

WuQiang,KongFanrang,HeQingbo,etal.EarlyFaultDiagnosisofRollingElementBearingBasedonWaveletTransformandIndependentComponentAnalysis[J].ChinaMechanicalEngineering, 2012, 23(7): 835-840.

[3]郑近德, 程军圣, 曾鸣, 等. 基于伪极值点假设的经验模态分解及其在转子故障诊断中的应用[J]. 中国机械工程, 2014，25(18): 2467-2472.

ZhengJinde,ChengJunsheng,ZengMing,etal.Pseudo-extrema-basedEMDandItsApplicationtoRotorFaultDiagnosis[J].ChinaMechanicalEngineering, 2014，25(18): 2467-2472.

[4]SmithJS.TheLocalMeanDecompositionandItsApplicationtoEEGPerceptionData[J].JournaloftheRoyalSocietyInterface, 2005, 2(5)：443-454.

[5]张亢, 程军圣, 杨宇. 基于局部均值分解的阶次跟踪分析及其在齿轮故障诊断中的应用[J]. 中国机械工程, 2011, 22(14):1732-1736.ZhangKang,ChengJunsheng,YangYu.OrderTrackingAnalysisbasedonLocalMeanDecompositionandItsApplicationstoGearFaultDiagnosis[J].ChinaMechanicalEngineering, 2011, 22(14):1732-1736.

[6]程军圣, 张亢, 杨宇. 局部均值分解方法及其在滚动轴承故障诊断中的应用[J]. 中国机械工程, 2009，20(22):2711-2717.

ChengJunsheng,ZhangKang,YangYu.LocalMeanDecompositionandItsApplicationstoRollingBearingFaultDiagnosis[J].ChinaMechanicalEngineering, 2009，20(22):2711-2717.

[7]郑近德, 程军圣, 杨宇. 部分集成局部特征尺度分解:一种新的基于噪声辅助数据分析方法[J]. 电子学报, 2013, 41(5)：1030-1035.

ZhengJinde,ChengJunsheng,YangYu.PartlyEnsembleLocalCharacteristic-ScaleDecomposition:aNewNoiseAssistedDataAnalysisMethod[J].ActaElectronicaSinica. 2013, 41(5)：1030-1035.

[8]来五星, 轩建平, 史铁林, 等.Wigner-Ville时频分布研究及其在齿轮故障诊断中的应用[J]. 振动工程学报，2003, 16(2)：147-250.

LaiWuxing,XuanJianping,ShiTielin,etal.ResearchofWigner-VilleTimeFrequencyandApplicationinDetectingGearPinionFault[J].JournalofVibrationEngineering, 2003，16(2)：147-250.

[9]YanRQ,GaoRX,ChenX.WaveletsforFaultDiagnosisofRotaryMachines：aReviewwithApplications[J].SignalProcessing, 2014, 96：1-15.

[10]于德介, 程军圣, 杨宇. 机械故障诊断的Hilbert-Huang变换方法[M]. 北京：科学出版社, 2006.

[11]雷亚国. 基于改进Hilbert-Huang变换的机械故障诊断[J]. 机械工程学报, 2011, 47(5)：71-77.

LeiYaguo.MachineryFaultDiagnosisBasedonImprovedHilbert-HuangTransform[J].JournalofMechanicalEngineering, 2011, 47(5)：71-77.

[12]程军圣, 郑近德, 杨宇. 基于局部特征尺度分解的经验包络解调方法及其在机械故障诊断中的应用[J]. 机械工程学报, 2012, 48(19)：87-94.

ChengJunsheng,ZhengJinde,YangYu.EmpiricalEnvelopeDemodulationApproachBasedonLocalCharacteristic-scaleDecompositionandItsApplicationstoMechanicalFaultDiagnosis[J].JournalofMechanicalEngineering, 2012, 48(19):87-94.

[13]GillesJ.EmpiricalWaveletTransform.IEEETransactionsonSignalProcessing[J]. 2013, 61(16)：3999-4010.

[14]GillesJ,TranG,OsherS. 2DEmpiricalTransforms:Wavelets,RidgeletsandCurveletsRevisited[J].SIAMJournalonImagingSciences, 2014, 7(1)：157-186.

[15]GillesJ,HEALK.AParameterlessScale-spaceApproachtoFindMeaningfulModesinHistograms-applicationtoImageandSpectrumSegmentation[J].InternationalJournalofWaveletsMultiresolutionandInformationProcessing, 2014, 12(6)：1450044(1-17).

[16]LindebergT.Scale-spaceTheoryinComputerVision[M].Berlin:Springer, 1994.

[17]WuZH,HuangNE.EnsembleEmpiricalModeDecomposition:aNoise-assistedDataAnalysisMethod[J].AdvancesinAdaptiveDataAnalysis, 2011, 1(1)：1-41.

[18]HuangNE,WuZ,LongSR,etal.OnInstantaneousFrequency[J].AdvancesinAdaptiveDataAnalysis, 2009, 1(2)：177-229.

[19]程军圣. 基于Hilbert-Huang变换的旋转机械故障诊断方法研究[D]. 长沙：湖南大学, 2005.

[20]胡爱军, 安连锁, 唐贵基. 转子碰摩故障振动时频特征的实验研究[J]. 动力工程学报, 2007, 27(4)：482-486.

HuAijun,AnLiansuo,TangGuiji.ExperimentalStudyonTime-frequencyCharacteristicsofRubbingInitiatedVibrationofRotor[J].JournalofPowerEngineering, 2007, 27(4)：482-486.

(编辑卢湘帆)

AdaptiveParameterlessEmpiricalWaveletTransform(EWT)andItsApplicationstoFaultDiagnosisofRotorSystem

ZhengJinde1PanHaiyang1PanZiwei1LuoJiesi2

1.AnhuiUniversityofTechnology,Maanshan,Anhui,243032 2.XiamenUniversityofTechnology,Xiamen,Fujian,361024

TofulfillanadaptiveseparationofFourierspectruminEWT,anadaptiveparameterlessEWT(APEWT)methodwasproposedherein.ToovercometheshortcomingsofHilberttransformandestimatemoreaccuratetime-frequencydistributionofagivensignal,animprovednormalizedHilberttransform(INHT)wasputforward.TheproposedAPEWTandINHTwerecomparedwithempiricalmodedecomposition(EMD),ensembleEMD(EEMD)andlocalcharacteristic-scaledecomposition(LCD)methodsandtheanalysisresultsdemonstratetheeffectivenessoftheproposedmethod.Finally,APEWTandINHTbasedtime-frequencyanalysismethodwereappliedtolocalrubbingfaultdiagnosisofarotorsystem,andtheanalysisresultsofexperimentaldataindicatethattheproposedmethodmayfulfillrotorrubbingfaultdiagnosiseffectivelyandhavebettereffectivenessthanthatofEMDandEEMDmethods.

rotorfault;rubbing;empiricalmodedecomposition;Hilberttransform

2016-01-08

国家自然科学基金资助项目(51505002)；安徽省高校自然科学研究重点项目(KJ2015A080)；福建省自然科学基金资助项目(2014J05065)

TH165.3; TN911.7

10.3969/j.issn.1004-132X.2016.16.016

郑近德，男，1986年生。安徽工业大学机械工程学院讲师、博士。主要研究方向为非线性动力学、动态信号处理和机械故障诊断等。发表论文近40篇。潘海洋，男，1989年生。安徽工业大学机械工程学院助教、硕士。潘紫微，男，1956年生。安徽工业大学机械工程学院教授。罗洁思，女，1985年生。厦门理工学院机械与汽车工程学院副教授。