基于压电陶瓷的柔性机械臂振动主动控制最优位置的设计
2016-09-07杨春来安徽工程大学机械与汽车工程学院安徽芜湖241000
薛 彬,王 海,杨春来(安徽工程大学机械与汽车工程学院,安徽芜湖 241000)
基于压电陶瓷的柔性机械臂振动主动控制最优位置的设计
薛彬,王海∗,杨春来
(安徽工程大学机械与汽车工程学院,安徽芜湖241000)
首先,基于弹性力学理论建立了主动抑振系统的动力学模型,并对其前三阶振型进行了数值仿真分析;其次,根据三阶振型曲线及仿真分析,确定了PZT传感器和驱动器的粘贴位置;最后,基于NI虚拟仪器搭建了抑振效果测试平台.实验测试结果显示,柔性机械臂在一阶固有频率下振动时根部抑振效果最佳,抑振率为44.51%,该实验为后续柔性臂在二阶、三阶固有频率下抑振方案的有效性分析与验证提供了良好的基础.
柔性机械臂;压电陶瓷;主动抑振;最优位置
机械结构可以分为刚性结构和柔性结构,刚性结构因其质量高、硬度大,运动时常被假设为刚体进行建模.然而,在构件高速运动的场合这种假设失效[1].柔性构件相比于刚性构件具有轻质、高效、低能耗的优点,更适用于柔性机器人高速运动的领域.但机构的低阻尼和高柔性,易破坏柔性机器人的工作精度和稳定性.柔性结构的抑振方法可分为主动控制和被动控制[2],基于开环系统的被动控制有较高的稳定性且易于实现.常见的被动控制方式有被动隔离和阻尼控制两种.Harris[3]在振动体和基座之间增加了隔离橡胶垫,Soong和Nakra[4]使用分流阻尼回路来降低系统的振动.被动控制对高频振动有明显的抑制效果,但并不适用于低频振动的领域.
主动控制弥补了被动控制的不足,能够有效地抑制低频振动,并且适用于系统参数实时改变的领域[5].主动控制涉及多种技术领域,例如一个典型的主动控制系统是由基于计算机和微处理器控制的机械元件和电子元件组成,其控制原理是使用驱动器产生的动能抑制系统的振动.主动控制的驱动器可以作用在柔性机器人的关节和柔性机械臂上.柔性关节的主动控制是通过关节处步进电机反转产生的转矩抑制柔性机构的转动.John[6]通过实验平台验证了柔性机构在一定的转角及运动速度内柔性关节控制的稳定及可靠性.柔性臂的主动控制基于智能材料作为传感器和驱动器实现.
压电陶瓷(PZT)作为常用的智能材料具有结构简单、体积小、轻质高效等优点.Crawley和De Luis[7]首次提出使用PZT传感器和PZT驱动器粘贴在柔性臂的表面,并通过闭环控制抑制柔性机械臂的振动.基于压电材料的控制器能够适用于较大频率范围内的抑振,对于不同频率的振动,柔性臂抑振的最优位置也是不同的.朱灯林[8]基于移动渐近线法(MMA)及曹玉岩[9]基于线性二次最优控制理论(LQG)研究柔性臂主动控制的最优位置.
根据柔性悬臂梁的前三阶振型分别确定前三阶振动下主动控制的最优位置,4个PZT驱动器粘贴在柔性臂的表面,通过不同位置的PZT驱动器工作来抑制柔性臂的前三阶振动.以一阶振动为例,通过仿真实验验证柔性臂在一阶振动时根部为其最优抑振位置.
1 理论建模
以单自由度的柔性机构为例,研究基于压电材料的柔性机构振动的主动控制.根据欧拉伯努利理论,可将单自由度的柔性机构看作一个悬臂梁进行建模.粘贴了PZT传感器与PZT驱动器的悬臂梁如图1所示.由图1可知,截面为矩形的悬臂梁在x=0处为固定端,x=L处为自由端.PZT驱动器以及PZT传感器被粘贴在悬臂梁的上下表面.Xai为第i片驱动器的初始位置,Xsi为第i片传感器的初始位置;L为悬臂梁的长度;l为压电片的长度.

图1 粘贴了PZT传感器与PZT驱动器的悬臂梁
柔性臂的动力学方程为:
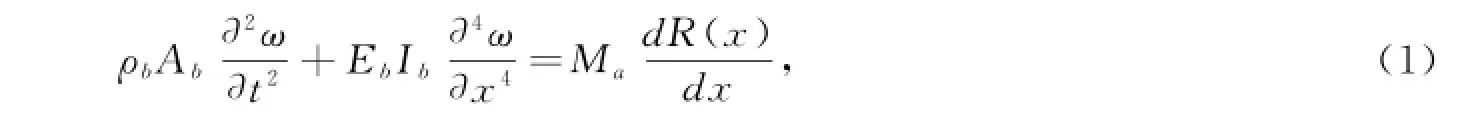
式中,R(x)为弯矩的位置方程;ρb为质量矩阵;Ab为梁横截面积;Eb为杨氏模量;Ib为转动惯量;横向位移ω(x,t)可以用无穷级数来表示:

式中,ηi(t)为时间函数;ϕi(x)为悬臂梁的第i阶振型.

式中,前3个常数值为λ1=1.875 1,λ2=4.694 0,λ3=7.854 7.
2 模态分析及抑振策略分析
在Comsol中,构建悬臂梁与PZT驱动器的模型,其参数如表1所示.

表1 柔性臂与压电材料的参数
通过数值仿真获得悬臂梁的前三阶振型,其固有频率分别为32 Hz、100 Hz、252 Hz,其振型图如图2所示.由图2可知,悬臂梁一阶振动时的根部应变最大;二阶振动时悬臂梁的中间部分有最大变形;三阶振动时柔性臂两处应变最大.图2中4处最大应变位置附近分别添加PZT驱动器并施加相应频率下幅值恒定的正弦电压,确定能使柔性臂产生最大动能的作用位置,分别距夹紧端0、80 mm、160 mm与230 mm.在此4处位置粘贴4个PZT驱动器,如图3所示.以柔性臂系统的动能大小为振动强弱的判断依据,因此省略PZT传感器.由图3可知,PZT1粘贴在一阶振动时的最大应变处抑制一阶振动,PZT3位于臂中间位置抑制二阶振动,PZT2和PZT4同时工作以抑制三阶振动.4片PZT驱动器分别位于柔性臂不同频率振动下最大应变位置.以一阶振动为例,研究根部抑振策略对柔性臂振动抑制的有效性,并分析其他3处位置的PZT驱动器对一阶振动的抑制效果,根据系统抑振前后动能变化曲线图判断其抑振效率.
定义抑振效率为:

式中,N为峰值数;pij为第j个压点片的第i个峰值;pio为开环响应的第i个峰值.
一个幅值为1 mm的正弦位移信号作用在柔性臂的夹紧端(x=0 mm)使其振动,频率设定为32 Hz.由于PZT驱动器的安全使用电压在20 V以内,以幅值为10 V的连续正弦电压为例分别作用在4个PZT驱动器上,频率与振动频率一致,产生弯矩模拟闭环控制,以验证PZT材料对柔性臂振动抑制的效果.获得柔性臂系统的动能比较图如图4所示.由图4可知,当柔性臂一阶振动时,系统开环响应的动能最大,最大峰值为0.002 3 J;位于悬臂梁根部的PZT1对柔性臂抑振时,系统的动能最小,最大峰值为0.000 8 J,抑振效果最佳;PZT3控制时,抑振效果较弱,最大峰值为0.001 1 J;PZT2和PZT4的抑振效果最弱,其最大峰值分别为0.001 5 J和0.002 J.根据仿真结果,不同位置的PZT驱动器对柔性臂抑振效率如表2所示.

图2 悬臂梁前三阶振型图

图3 控制器设计图

图4 柔性臂系统的动能比较图

表2 PZT驱动器在不同布局模式下的系统抑振效率的比较
3 实验研究
以不同位置的PZT驱动器对一阶频率振动的柔性机械臂抑振效果的对比为研究内容,实验设备主要由柔性机械臂、PZT传感器、PZT驱动器、信号发生器、功率放大器、激振台、压电陶瓷驱动电源以及数据采集平台组成,其装置如图5所示,实验系统的组成如表3所示.

表3 实验系统组成元件
系统工作时,其系统框图如图6所示.由图6可知,由信号发生器产生信号,传输到功率放大器将信号放大并驱动激振台带动柔性机械臂夹紧端产生正弦振动.粘贴在柔性臂上的PZT传感器通过正压电效应将柔性臂的振动信号转换成电信号并由电荷放大器放大后,数据采集卡将连续的模拟量转换为数字量传递到计算机.计算机输出正弦电压到压电陶瓷驱动电源,驱动粘贴在柔性臂表面的PZT驱动器产生弯矩形成闭环控制,最终实现对柔性臂振动的抑制.

图5 柔性机械臂抑振实验装置图
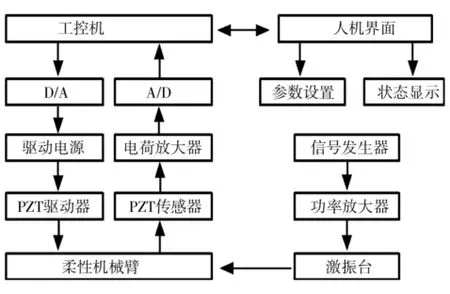
图6 实验控制系统框图
为了研究PZT驱动器,应着重关注PZT传感器应用于柔性机械臂振动控制策略的有效性,以及当柔性臂在一阶固有频率下振动驱动器粘贴于不同位置对抑振效果的影响.在本实验中,于机械臂的一侧粘贴4片PZT驱动器,分别位于距离悬臂梁夹紧端0、80 mm、160 mm和230 mm处,同时与仿真部分4片PZT驱动器的粘贴位置应该保持一致.在机械臂的另一侧距离夹紧端0粘贴一个PZT传感器.控制器装置如图7所示.

图7 控制器装置图
调节信号发生器和功率放大器使激振台带动悬臂梁夹紧端产生幅值为1 mm、频率为32 Hz的正弦振动,传感器产生了幅值为0.5 V、频率为32 Hz的电压信号.将与仿真部分相一致的驱动电压信号10sin(64pi∗t)V分别作用在4片PZT驱动器上抑制柔性臂的振动,实验结果如图8所示.由图8可知,柔性臂在一阶振动时,开环响应的传感电压最大达0.5 V;PZT1抑振时传感电压最小0.24 V;PZT3抑振时得到较小的传感电压0.37 V;PZT2和PZT4抑振时传感电压为0.4 V和 0.41 V.根据实验及仿真数据可得不同位置的PZT驱动器对柔性臂抑振效果,如表4所示.由表4可知,当柔性臂产生频率为32 Hz的一阶振动时,位于根部0处的PZT1驱动器抑振效果最佳,位于160 mm处的PZT3抑振效果其次,位于80 mm及230 mm处的PZT2与PZT4抑振效果最弱.
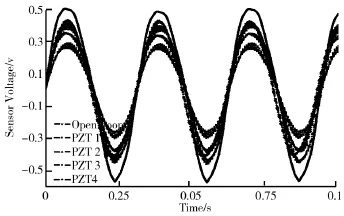
图8 PZT驱动器在不同布局模式下的传感器输出电压对比

表4 不同位置PZT驱动器作用下柔性机械臂的抑振效率
4 小结
通过构建一个粘贴有PZT驱动器与PZT传感器的柔性机械臂的理论模型,在Comsol中进行数值仿真得到一阶振动的振型,应变最大的位置在柔性臂的根部.4个不同位置的PZT驱动器粘贴在柔性臂的表面,进行闭环控制抑制柔性臂的振动.在Comsol中的仿真结果和实验平台获得的数据得到了相同的结论:一阶振动时,柔性臂根部的抑振效果最佳.后期将着眼于对二阶与三阶固有频率振动下柔性臂的最佳抑振位置进行验证.
[1]M Khairudin,Z Mohamed,Z M Zain.Modeling of a Two-link Flexible Manipulator[J].Instrumentation and Mechatronic Engineering,2009,35(17):191-199.
[2]J X Fan,Y Z Yin.Composite Control Method for Active Vibration Suppression of Tethered Spacecraft[J].WIT Transactions on Information and Communication Technologies,2014,36(10):1 113-1 121.
[3]Francisco Palacios-Qui Nonero,Hamid R Karimi,Josep Rubio-Massegu.Passive-damping Design for Vibration Control of Large Structures[C]//Hangzhou:IEEE International Conference on Control and Automation,2013,60:33-38.
[4]Djojodihardjo Harijono,Jafari Mohammad,Wiriadidjaja Surjatin.Active Vibration Suppression of an Elastic Piezoelectric Sensor and Actuator Fitted Cantilevered Beam Configurations as a Generic Smart Composite Structure[J].Composite Structures,2015,158(2/3):848-863.
[5]J Chacon,M Beschiy,J Sanchez,et al.Experimental Analysis of a Remote Event-based PID Controller in a Flexible Link System[J].IEEE Emerging Technology and Factory Automation,2014,4(8):1-6.
[6]John TAgee,Zafer Bingul,Selcuk Kizir.Tip Trajectory Control of a Flexible-link Manipulator Using an Intelligent Proportional Integral(iPI)Controller[J].Transactions of the Institute of Measurement and Control,2004,36(10):2 942-2 947.
[7]E F Crawley,J D Luis.Use of Piezoelectric Actuators as Elements of Intelligent Structures[J].AIAA Journal,1987,89(2/3):1 373-1 385.
[8]朱灯林,吕蕊,俞洁.压电智能悬臂梁的压电片位置尺寸及控制融合优化设计[J].机械工程,2009(2):262-267.
[9]曹玉岩,王志臣,付世欣,等.智能桁架结构最优振动控制与作动器优化配置[J].振动与冲击,2015(5):26-32.
Design for Optimal Position of Vibration Control for a Flexible Beam Using PZT Patches
XUE Bin,WANG Hai∗,YANG Chun-lai
(College of Mechanical and Automotive Engineering,Anhui Polytechnic University,Wuhu 241000,China)
An active suppression method based on PZT patches was proposed and a single link manipulator was employed to illustrate the efficiency of this vibration control method.This system was composed of a single link flexible beam,PZT sensors and PZT actuators.Firstly,a theoretical model of a single link flexible manipulator with PZT patches was set up and the first three mode shapes were obtained with numerical simulation.Furthermore,the position of PZT sensors and actuators were figured out according to these three mode shapes.Finally,an experiment platform was set up based on the NI virtual instrument and the result of experiment showed that:the optimal position of vibration control for a flexible beam moving at the first frequency occurs at the fixed end of the beam and the system can get 44.51% vibration suppression.This work provides a foundation for further research of vibration control at the second and third frequency.
flexible beam;PZT sensors and actuators;active suppression;optimal position
TH16,TP24
A
1672-2477(2016)04-0042-05
2015-12-17
国家自然科学基金资助项目(51275001,51375469)
薛彬(1990-),男,江苏南京人,硕士研究生.
王海(1976-),男,安徽芜湖人,教授,硕导.
