碳限额与交易机制下供应商-制造商生产决策研究
2016-09-07汤家骏龚本刚安徽工程大学管理工程学院安徽芜湖241000
汤家骏,龚本刚,刘 志(安徽工程大学管理工程学院,安徽芜湖 241000)
碳限额与交易机制下供应商-制造商生产决策研究
汤家骏,龚本刚∗,刘志
(安徽工程大学管理工程学院,安徽芜湖241000)
考虑由供应商和制造商构成的两级供应链系统,研究碳限额与交易机制下供应商领导的供应链生产决策问题.在碳限额与交易机制下,运用Stackelberg博弈理论,以供应商为领导者,分别给出在分散决策和集中决策时各自以自身收益最大化为目标的最优生产决策,得出供应商和制造商同时达到生产决策的临界点.通过无碳排放约束和碳限额与交易机制的比较,说明碳限额与交易机制能够在一定范围内起到减少碳排放的作用,并通过算例验证了结论的正确性.
生产决策;供应链;碳限额与交易机制;Stackelberg博弈
随着人口数量急剧增长及现代化工业进程的加快,不仅能源消耗与日俱增,温室气体(CO2、N2O、CH4)的排放也给环境带来了严重的破坏,威胁着人类的生存和发展.二氧化碳作为温室气体的主体,其减排的重要性和紧迫性已经得到全球范围内的普遍共识和高度关注.经过国际社会的共同努力,围绕气候变化问题的国际峰会得以定期召开,目前已经形成一系列具有法律约束力的国际公约.如2005年《京都议定书》设定了一种通过管制和市场双重手段以有效达到减排效果的减排机制,即碳限额与交易机制[1].2010年我国制造业产出占世界比重为19.8%,超过美国成为全球制造业第一大国[2].但制造业一直是我国能耗大户,我国制造业的高增长、高产值是以高能耗和高排放为代价的[3].改革开放以来,我国节能减排工作重点就已经放在工业领域,特别是高耗能的制造行业[4],因此,制造型企业自然承担了减排的重任.国内外学者对于企业如何减少碳排放做了大量的研究,并取得丰硕的成果[5-14].然而研究主要以单个企业或供应链中供应商和零售商组成的供应链为研究对象,大都从单个企业或供应链某一方为碳限额方而展开,而在碳排放限额与交易机制的约束下,同时考虑供应链的供应商和制造商双方的生产决策问题研究较少涉及.为此,同样在碳限额与交易机制下,运用Stackelberg博弈理论算法研究由供应商和制造商组成的供应链系统分别在分散决策和集中决策时以自身收益最大化为目标进行最优生产决策,同时以无碳排放约束下供应链最优生产决策为参照,说明碳限额与交易机制能够起到降低碳排放的作用,得出供应商和制造商分别在分散决策和集中决策的一致性.最后通过算例验证结论的正确性.
1 问题描述与基本假设
考虑在单周期内由单个供应商和单个制造商组成的两级供应链系统,该供应商向制造商提供主要组件,制造商在此基础上进行产成品的制造,通过协同合作来生产一种产品.研究在双方都受到碳限额约束条件下的最优生产决策问题.
在碳限额与交易机制下,供应商和制造商在生产期前同时获得政府环保部门分配的碳限额Qs、Qm.供应商和制造商可以在碳交易市场上或内部之间进行碳排放权交易.单位碳交易市场价格pe,碳交易量分别为Ts、Tm(若为正,表示从碳交易市场购入碳排放权;若为负,表示售出碳排放权;若为零,表示不进行碳排放权交易).供应商生产主要组件的单位成本cs、产生碳排放量es、碳排放总量Es,并以批发价w将主要组件提供给制造商(w为供应商的决策变量);制造商在供应商提供主要组件的基础上进行最终产品的生产制造.供应商生产产品的单位成本cm、产生的碳排放量em、总碳排放量Em、制造商的加成定价量u(u为制造商的决策变量),以单位产品价格为p销售给顾客(价格p受w和u的共同影响),显然p=w+u.不失一般性,有p>w≥cs>0,p>u≥cm>0.其关系如图1所示.
为了便于问题的研究,作如下假设:
假设1该供应链由单个供应商和单个制造商组成,供应商和制造商相互依存,且每个产成品由单个供应商提供的主要部件和其他部件组成;
假设2供应商和销售商都完全掌握产品相关信息.产品的市场需求量为q=K-βp,其中,K为产品潜在的需求量;β为顾客的价格敏感系数;且K、β>0.
假设3文中单位产品生产成本cs、cm为平均成本,包括制造成本、库存成本、运输成本等;同理,单位产品碳排放量es、em同样为制造、库存、运输等过程产生的碳排放量的平均数.
文中使用的主要符号及其含义如表1所示.

图1 碳限额与交易机制下供应商和生产商关系

表1 主要符号及其含义
2 模型建立与求解
考虑分别在无碳排放约束(N)和碳限额与交易机制(T)下,研究供应商(S)和制造商(M)在分散决策(D)及集中决策(C)时的最优决策.为了表述方便,分别用N-D、N-C、T-D、T-C来代替不同的限制条件和决策机制(如N-D表示无碳排放约束下进行分散式最优生产决策).
假设供应商和制造商在供应链中的地位不平等.供应商向制造商供应主要部件,具有更多的话语权,不妨假设供应商为主导者,制造商为跟随者.供应商和制造商都以各自收益最大化为目标,使用逆向归纳法进行求解,进行Stackelberg博弈最优生产决策.
2.1无碳排放约束的供应链企业最优生产决策模型
在无碳排放约束机制下,供应商和制造商在不受碳排放约束下进行生产决策为传统的生产决策问题.
(1)分散决策模型(N-D).在N-D下,供应商、制造商以及整条供应链的目标函数分别为:



命题1验证了Stackelberg博弈中的“先发优势”,即在Stackelberg博弈中领导者可能占有获得更多效益的优势,这也是各企业争当领导者的主要原因.
(2)集中决策模型(N-C).在N-C下,将该供应链看成一个整体,以收益最大化为目标进行最优生产决策研究.此时供应商的批发价格w和制造商产品价格加成量u属于内生变量,可以相互抵消,故在此不予考虑.
在N-C下,供应链的目标函数为:

命题2说明在无碳排放约束下,集中决策时供应链收益要大于分散决策时供应链收益,使供应商和制造商有更多收益进行分配;同时,集中决策时的产品价格更低,而市场需求量更高;对于消费者来说,可以满足更多消费者需求,获得更多消费者剩余.无论是从供应链的角度还是从消费者的角度来看,集中决策都要优于分散决策.然而集中决策产生更多的碳排放,不利于环保政策的实施.
2.2碳限额与交易机制下供应链企业最优生产决策模型
碳限额与交易机制下,供应商和制造商以其收益最大化为目标,可以自主在碳交易市场上进行碳排放权买卖.
(1)分散决策模型(T-D).在T-D下,供应商和制造商的收益最大化目标函数为:

引理1在T-D下,供应商和制造商进行生产决策的充要条件是各自的边际收益同时大于或等于相应的碳交易成本,即w-cs≥pees和u-cm≥peem同时成立.
引理1表示只有当供应商和制造商都进行生产决策时,才能实现供应链生产运作.在同一条供应链中,供应商和制造商之间相互依存.供应商依赖制造商来购买自己生产的产品,制造商依靠供应商提供生产所需的主要部件.如若一方不进行生产决策,即使另一方边际收益大于边际成本,也将无法进行生产决策.这说明供应链各参与者的决策需要协调一致的必要性.
推论1在T-D下,当单位碳交易价格pe发生变动时,供应商和制造商将同时达到是否进行生产决策的临界点.
推论1说明当单位碳交易价格pe发生变动时,供应商和制造商将同时达到生产决策的临界点.这保证了供应商和制造商生产决策的一致性,避免了一方进行生产决策而另一方不进行生产决策的矛盾.


(2)集中决策模型(T-C).在T-C下,供应链的收益最大化的目标函数为:

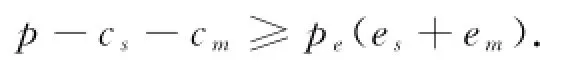
推论3当单位碳交易价格pe发生变动时,供应链在集中决策下和分散决策时将同时达到生产决策临界点
推论3说明当单位碳交易价格发生变动时,无论是在分散决策下还是集中决策下,都将同时进行生产决策或者不进行生产决策.

从推论4可以看出,当企业不进行生产决策时,集中决策和分散决策都有相同的结果,此时并没有体现出集中决策的优越性,碳限额与交易机制也没有起到限制碳排放的作用.
推论5在碳限额与交易机制下,供应商和制造商进行生产决策与政府分配的碳限额无关系,只与单位碳交易成本相关,并且p随着单位碳交易价格的增加而减少,直至为0.
推论5说明在碳限额与交易机制下,供应商和制造商的生产决策不受政府碳限额的影响,把政府分配的碳限额当作企业的固有资产,而把运营过程产生的碳排放成本当作附加成本.随着单位碳交易价格增大,导致生产成本随之增高,单位产品销售价格p也增加.由反需求函数得市场需求量q减小,所以生产决策受到碳交易价格的影响.但是需要注意的是,在碳交易市场上,单位碳交易价格受到政府所拥有的碳排放总量的影响.只是相对于单个企业或供应链来说,由于其获得的碳分配数量较小,对单位碳交易价格基本不产生影响.
从推论6可以看出,随着单位碳交易价格pe的逐渐增大,供应链的收益首先减小,然后增大.原因是当碳交易价格开始增大时,首先生产成本增加而导致收益减少;后来随着单位碳交易价格的不断上涨,使得政府分配的碳限额所占比重越来越大,使供应链从政府分配的碳限额部分获得的收益比例显著增加,导致收益增长.最后供应链的收益完全来自政府分配的碳限额.
从推论7可以看出,无论是在分散决策还是集中决策下,碳限额与交易机制下供应链总的碳排放小于无碳排放约束下供应链总的碳排放量,说明碳限额与交易机制能够起到限制企业碳排放的作用.
3 算例验证
为了对以上各结论进行验证,基于Matlab 7.0.1软件,通过各变量的不同取值来进行验证.不妨取K= 400、β=5、cs=12、cm=8、es=0.4、em=0.3.无碳排放机制下计算结果如表2所示.在碳限额与交易机制下,Qs、Qm和Pe的取值如表3所示.相应的计算结果如表4所示.

表2 无碳排放约束下各算例的计算结果

表3 各算例参数值

表4 碳限额与交易机制下各算例的计算结果
Ts=22、Tm=20时单位碳交易价格pe发生变动,对分散决策和集中决策下最优决策的影响如图2所示.从图2a中看出,当单位碳交易价格pe≤85.7时,供应商批发价w、制造商产品价格加成量u和产品销售价格p都随着pe的增大而增加,产品的销售数量q随着pe的增大而减小.原因是在碳限额与交易机制下,政府分配的碳限额被视作企业拥有的资源,而生产过程产生的碳排放费用被认为是附加生产成本,当单位碳交易价格pe逐渐增大时,其生产成本将会增大,所以w、u和p都随之增大;而当单位碳交易价格pe>85.7时,供应链将不会进行生产决策,而是售出政府分配的碳限额,故各变量值都为0.从图2b、图2c中可以看出,随着pe的增加,供应链的碳排放量和碳交易量都减小.从图2d中可以看出,随着pe的增加,供应链的收益首先减少,然后增加,当pe>85.7时,将会以相同的速率增加.

图2 单位碳交易价格对分散决策时最优解的影响
在碳交易价格变动时,集中决策和分散决策的对比如图3所示.从图3a中可以看出,集中决策和分散决策同时达到是否进行生产决策的临界点(p︵e=85.7).从图3b、图3c中可以看出,当pe≤p︵e时,无论是在集中决策下还是在分散决策下,供应链的碳排放量和碳交易量都随着pe的增加而减小,供应链的收益先减小,随后增大.当pe>p︵e时,供应链的碳排放量都为零,而碳交易量都等于政府分配的碳限额的总量,供应链的总收益为线性增加,并且分散决策和集中决策时供应链的收益相等.

图3 单位碳交易价格发生变动时分散决策和集中决策的比较
4 结论与展望
供应商作为供应链的一个重要组成部分,通过与制造商进行良好的协调合作,在取得良好经济效益的前提下,还可取得良好的环境效益.研究考虑在碳限额与交易机制下,由单个供应商和制造商组成的供应链系统的最优生产决策问题.以供应商和制造商在无碳排放约束下最优决策为参照对比,说明碳限额与交易机制能够在一定程度起到限制碳排放的作用,但并不是在所有情形下都能发挥作用.同时也得出,当单位碳交易价格增长到一定程度时,无论是在分散决策还是集中决策下,供应商和制造商都将同时达到是否进行生产决策的临界点,保证了供应商和制造商生产决策的一致性.通过集中决策和分散决策的对比,说明集中决策比分散决策能够获得更好的经济效益,但是从环境角度来说,集中决策会产生更多的碳排放.
研究尚存在以下局限性,将在今后加以完善.首先,为了突出供应商和制造商都作为碳依赖生产型企业而同时受到碳排放限制这一特点,而将其他一些因素加以忽略,如库存、运输等活动产生的成本和碳排放等;其次,基于理论研究,假设市场需求为已知的,而实际的市场需求是波动的,与实际情况不符.
[1]杜少甫,董骏峰,梁樑,等.考虑排放许可与交易的生产优化[J].中国管理科学,2009(3):81-86.
[2]苗圩.我国重返全球制造业第一大国[EB/OL].http://www.shantui.com/news/4316_for_xingyexinwen_text.htm,2012-09-18.
[3]王锋,吴丽华,杨超.中国经济发展中碳排放增长的驱动因素研究[J].经济研究,2010(2):123-136.
[4]中国能源和碳排放研究课题组.2050中国能源和碳排放报告[R].北京:科学出版社,2009.
[5]P Letmathe,N Balakrishnan.Environmental Considerations on the Optimal Product Mix[J].European Journal of Oper-ational Research,2005,167:398-412.
[6]G Hua,S Cheng.Managing Carbon Footprints in Inventory Management[J].International Journal of Production Economics,2011,132:178-185.
[7]J Zhang,T Nie,S Du.Optimal Emission-dependent Production Policy with Stochastic Demand[J].Int.J of Society Systems Science,2010,3(1/2):21-39.
[8]蓝海燕,戢守峰.限额与交易机制下厂商订货策略[J].系统工程,2013(12):81-86.
[9]马常松,陈旭,罗振宇,等.随机需求下考虑低碳政策规制的企业生产策略[J].控制与决策,2015(6):969-976.
[10]S Benjaafar,Y Li,M Daskin.Carbon Footprint and the Management of Supply Chains:Insights from Simple Models[J].Auto-mation Science and Engineering,2013,10(1):99-116.
[11]S Du,F Ma,Z Fu.Game-theoretic Analysis for an Emission-dependent Supply Chain in a"Cap-and-trad"System[J].Annals of Operations Research,2015,228(1):135-149.
[12]王芹鹏,赵道致.消费者低碳偏好下的供应链收益共享契约研究[J].中国管理科学,2014(9):106-113.
[13]徐春秋,赵道致,原白云.低碳环境下供应链差异化定价与协调机制研究[J].运筹与管理,2015(1):19-26.
[14]J Ren,Y Bian,X Xu,et al.Allocation of Product-related Carbon Emission Abatement Target in a Make-to-order Supply Chain[J].Computer and Industrial Engineeing,2014,80(1):181-194.
Production Decision of the Supplier-manufacturer under the Carbon Cap-and-trade Mechanism
TANG Jia-jun,GONG Ben-gang∗,LIU Zhi
(College of Management Engineering,Anhui Polytechnic University,Wuhu 241000,China)
Considering a two-stage supply chain system constituted by the suppliers and manufacturers,this paper studies the supply chain production decision problem dominated by the suppliers under the carbon cap-and-trade mechanism.In this situation,under the leadership of the suppliers,Stackelberg game theory is used to give optimal production decisions for maximizing their own profit respectively while making the decentralized decision and centralized decision.A conclusion is made that suppliers and manufactures would reach the critical point of production decisions at the same time.By comparing the non-carbon constraints and the cap-and-trade mechanism,the paper proves that the carbon cap-and-trade mechanism can reduce the carbon emission in a certain range.Finally,a numerical example is given to verify the correctness of the conclusion.
production decision;supply chain;carbon cap-and-trade mechanism;stackelberg game
F224
A
1672-2477(2016)04-0088-07
2015-10-30
安徽省自然科学基金资助项目(1308085 MG108)
汤家骏(1990-),男,安徽合肥人,硕士研究生.
龚本刚(1973-),男,安徽金寨人,教授,硕导.
