一种快速的中值滤波算法
2016-09-07马运强魏利胜张平改安徽工程大学电气工程学院安徽芜湖24000安徽机电职业技术学院电气工程系安徽芜湖24000
马运强,魏利胜,张平改,吉 涛(.安徽工程大学电气工程学院,安徽芜湖 24000,2.安徽机电职业技术学院电气工程系,安徽芜湖 24000)
一种快速的中值滤波算法
马运强1,2,魏利胜1∗,张平改1,吉涛1
(1.安徽工程大学电气工程学院,安徽芜湖241000,2.安徽机电职业技术学院电气工程系,安徽芜湖241000)
鉴于中值滤波算法中排序次数多、程序运行效率低的缺点,提出了一种快速的中值滤波算法.首先,利用统计理论排序法对滤波窗口的像素全面排序比较;在此基础上,利用相邻滤波窗口行列信息之间的相关性原理,通过迁出、移入一列新像素,同时保留剩余列像素的排序信息,从而快速查找到滤波窗口的中值;最后,通过仿真实验对比得出所提算法有效地降低了排序比较次数和算法的复杂度,满足图像处理的实时性.
滤波窗口;中值;排序比较;算法
在数字图像处理中,由于背景光照不均、电气设备磁场信号干扰等原因,采集的图像存在很多随机噪声[1-3].而随机噪声不仅降低了图像的质量与美感,还影响后期数字图像的灰度化、边缘检测、图像分割、图像拼接等.为了提高图像的效果和美感,需要对图像进行预处理,如图像增强、图像滤波、图像平滑等.而中值滤波是剔除图像噪音、改善图像质量最有效措施之一.中值滤波是一种典型的非线性滤波技术,不但可以有效地抑制多种图像噪音,而且能有效地保留图像边缘细节信息,故其得到了广泛地运用和推广.但是标准的中值滤波算法由于算法排序量大,运算速度缓慢,不能实时高效地抑制图像噪音.因此,如何降低中值滤波排序比较次数具有重要的研究意义.

1 标准的中值滤波算法
标准中值滤波算法原理[10-12]:数字图像窗口某点像素领域内滤波窗口所有像素按照灰度值大小进行排序,排序后中间位置的灰度值即为中值,用中值代替原像素的灰度值.若滤波窗口的像素个数为偶数,则排序后两个中间位置灰度值的平均值即为中值.标准中值滤波窗口是N(N取奇数)维的移动的窗口,滤波窗口从左往右,从上往下滑动.对于一幅N×M的数字图像用矩阵形式表示为F,如式(1)所示:

若3×3滤波窗口的中心元素为(i,j),则3×3滤波窗口用矩阵表示为E(i,j),如式(2)所示:


其中,h(x,y)表示滤波后图像;f(x,y)表示原图像;E(i,j)表示滤波窗口;(i,j)表示滤波窗口的中心像素点;i表示滤波窗口水平尺度;j表示窗口垂直尺度.

2 改进的中值滤波算法
以上标准的中值滤波算法虽然降低了滤波窗口查找中值的比较次数,但是比较次数依然较多.排序算法的优劣直接影响着查找中值的效率,为了以更低的比较次数查找中值,提出一种快速的中值滤波算法.该算法充分利用统计理论排序法和相邻窗口行列信息相关原理进行排序,可以更加高效地降低滤波窗口查找中值的比较次数.
首先利用统计理论排序法查找滤波窗口的中值,然后利用相邻窗口行列信息相关性的原理进而查找f(i,j)像素滤波窗口的中值.其整体查找中值效率将优于以上算法,排序比较次数更低.利用统计理论排序法对滤波窗口进行排序,滤波窗口共有9个像素,排列成3列3行.将3列像素按照向下升序排列得到3组新序列,将3组新序列按照f(i,j-1)、f(i,j)、f(i,j+1)像素大小向右升序排组,得到最终排序滤波窗口.虚线箭头方向为升序方向,如图1所示.
对最终排序得到滤波窗口进行分析,f(i-1,j-1)不可能是中值,因为f(i-1,j-1)像素值小于窗口的其他6个像素值(f(i,j-1)、f(i,j)、f(i,j+1)、f(i+1,j-1)、f(i+1,j)、f(i+1,j+1)).由于f(i,j-1)的像素值小于窗口的其他5个像素(f(i,j)、f(i,j+1)、f(i+1,j-1)、f(i+1,j)、f(i+1,j+1)),因此f(i,j-1)不是中值.同理可知f(i,j+1)和f(i+1,j+1)也不可能是中值,因为f(i,j+1)和f(i+1,j+1)至少大于窗口其他的5个像素值,因此滤波窗口的中值应该在f(i-1,j)、f(i-1,j+1)、f(i,j)、f(i+1,j-1)、f(i+1,j)之中.当f(i-1,j+1)和f(i+1,j-1)一个大于f(i,j),另一个小于f(i,j)时,或者f(i-1,j+1)和f(i+1,j-1)同时等于f(i,j)时,则f(i,j)为滤波窗口的中值,且比较次数为2次.当f(i-1,j+1)和f(i+1,j-1)同时大于f(i,j)时,则f(i,j)、f(i-1,j+1)、f(i+1,j-1)最小值为滤波窗口的中值,或者f(i-1,j+1)和f(i+1,j-1)同时小于f(i,j)时,则f(i,j)、f(i-1,j+1)、f(i+1,j-1)的最大值为滤波窗口的中值,且比较次数为4次.3列像素向下升序排序比较需要9次,3组新序列按照f(i,j-1)、f(i,j)、f(i,j+1)像素值大小向右升序排组,排序比较次数需要3次,因此利用统计理论排序法进行排序最好排序比较次数需要14次,最坏排序比较次数需16次.
为了以更低的比较次数查找窗口中值,利用相邻窗口行列信息相关性的原理进一步排序,同时进一步降低滤波窗口整体的排序次数.设当前滤波窗口为E(i,j),沿水平方向移动后的滤波窗口为E′(i,j+1).滤波窗口E′(i,j+1)在第j+2列移入一列新像素,同时移出E(i,j)对应第j-1列像素,如图2所示.滤波窗口E′(i,j+1)的第j和j+1列像素的排序信息是已知,因此对于滤波窗口E′(i,j+1)无需再次排序比较j和j+1列像素,其步骤如下所示:
(1)对滤波窗口E′(i,j+1)更新的第j+2列像素按照向下升序排序.滤波窗口E′(i,j+1)第j和j+1列像素排序信息未变,只需将第j+2列像素与第j和j+1列像素比较;
(2)将第j和j+1及j+2列像素按照f(i,j)、f(i,j+1)、f(i,j+2)像素值向右升序排列;
(3)最后运用上述统计理论排序法可快速查找到中值,查找滤波窗口E′(i,j+1)中值,第j+2列像素需排序比较3次,3列像素按照行中心值大小需排序比较2次,分析剩余像素排序比较次数最坏需4次,最优需2次.
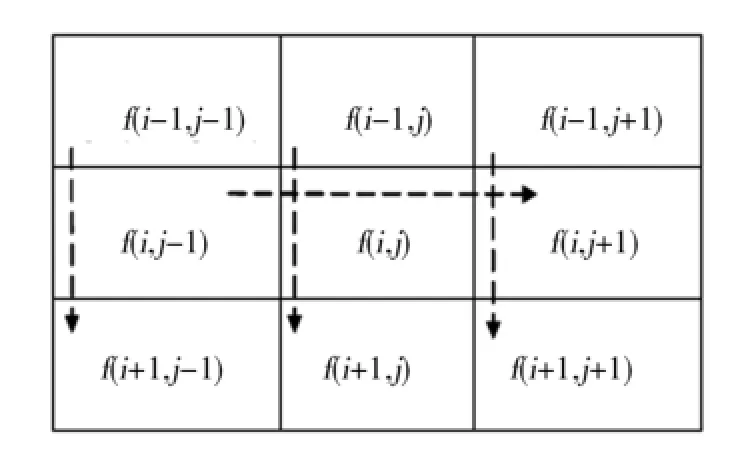
图1 3×3滤波窗的排序
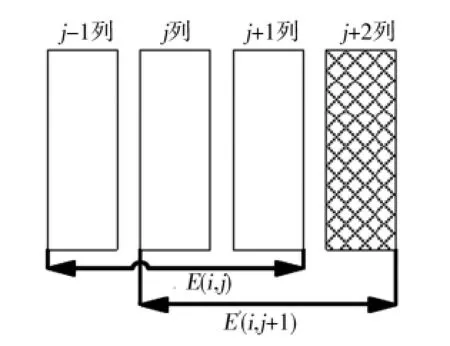
图2 滤波窗口E(i,j)及E′(i,j+1)
3 算法复杂度的优劣对比
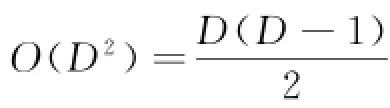
由于所提出算法选取滤波窗口为3×3,可知滤波窗口E′(i,j+1)最坏排序比较次数需要9次,最优排序比较次数需7次.当滤波窗口需要查找某行中的m个像素的中值,则滤波窗口最坏排序比较需要16+9(m-1)次,最优排序比较需要14+7(m-1)次.当m趋于无穷大,则滤波窗口最优排序比较需要7m次,最坏排序比较需要9m次.
4 仿真实验
为了验证所提出算法的可行性,仿真实验对3 264×2 248 School图像和512×512 Lena图像分别采用所提出的算法和传统的中值滤波算法进行仿真.实验平台计算机为Window 7系统,2 GB内存,程序运行环境为Matlab 7.11.School和Lena图像滤波效果分别如图3和图4所示.图3a和图4a分别为School和Lena源图像;图3b和图4b分别为School和Lena图像加入20%椒盐噪音的效果;图3c和图4c分别为School和Lena图像运用所提算法处理后效果;图3d和图4d分别为School和Lena图像运用Matlab中3×3标准中值滤波算法处理后的效果.通过图3b和图3c对比可以得出所提出的算法具有良好去噪能力,同时可以较好地保留细节信息;通过图4c和图4d对比得出所提出的算法可以去除标准中值滤波算法难以过滤的噪音.
中值滤波算法的复杂度与算法查找滤波窗口中值的排序次数成线性关系,有效降低排序比较次数,可降低算法的时间复杂度.为了进一步说明所提出方法的优越性,算法的复杂度和效率指标如表1所示,由表1可知,查找单个像素中值冒泡法的复杂度为36次,文献[4]方法复杂度为30次,所提出算法在最优情况下复杂度为14次.查找m个像素中值冒泡法的复杂度为36m次,所提出算法在最优情况下复杂度为7m次,效率提高了80.5%.冒泡法处理School图像所需时间为1.237 s,所提出算法在最优情况下处理School图像所需时间为0.572 s,所提出算法处理School图像时间复杂度只有冒泡法的46.24%.因此,所提出算法处理滤波窗口查找中值所需次数最少.效率最高、算法复杂度最低.当查找中值的像素越多,所提出算法排序次数越少,效果越明显,时间复杂度越低.

图3 School图像滤波效果

图4 Lena图像滤波效果

表1 3×3滤波窗口查找中值各算法复杂度及效率
5 结论
鉴于标准中值滤波算法查找中值排序工作量大、运算速度慢、不能满足图像处理实时性,首先介绍了标准的中值滤波算法和一些改进中值滤波算法,进而提出一种快速的中值滤波算法.所提出算法首先利用统计理论排序法对滤波窗口像素排序,在此基础上利用滤波窗口行列信息相关性原理进一步进行排序比较.最后通过仿真实验得出所提算法抑制噪声能力强,滤波效果比较满意,算法时间复杂度较低.
[1]赵君爱,魏艳春.基于改进中值滤波的图像噪声去除算法的研究[J].浙江农业学报,2015,27(6):1 078-1 082.
[2]钟涛,张建国,左俊彦.一种改进的中值滤波算法及其应用[J].云南大学学报:自然科学版,2015,37(4):505-510.
[3]董恩增,吴东东,佟吉钢.快速二维中值滤波算法及其FPGA硬件设计[J].计算机工程与设计,2015,36(7):1 752-1 756.
[4]朱捷,朱小娟,贺明.基FPGA的实时性的图像处理中值滤波器设计实现[J].计算机测量与控制,2007,15(6):798-800.
[5]P J Wei,L Zhang.Fast Median Filtering Algorithm Based on FPGA[C]//Signal Processing(ICSP)2010 IEEE 10th International Conference on,USA:IEEE Press,2010:426-429.
[6]杨帆,张皓,马新文,等.基于FPGA的图像处理系统[J].华中科技大学学报:自然科学版,2015,2(2):119-123.
[7]王宇新,贺圆圆,郭禾.基于FPGA的快速中值滤波算法[J].计算机应用研究,2009,26(1):224-226.
[8]陈元朝,李丽宏.自适应滤波算法在车辆宽高检测系统中的应用研究[J].中国测试,2014,40(2):40-43.
[9]曾志刚,杨海,黄望军.基于自适应滤波与模糊PID的移动机器人导航研究[J].控制工程,2015,22(5):953-957.
[10]牛敏,邬建军,牛燕雄,等.一种基于排序统计理论的快速图像中值滤波法[J].电子测量技术,2015,38(6):60-63.
[11]X Geng,X G Hu.Quatertion Switching Filter for Impulse Noise Rsdution in Color Image[J].Signal Processing Letters,2012,92(1):150-162.
[12]H Yuan.Blind Forensics of Median Filtering in Digital Images[J].IEEE Transactions on Information Forensics and Security,2011,6(4):1 335-1 345.
A Fast Algorithm of Median Filter
MA Yun-qiang1,2,WEI Li-sheng1∗,ZHANG Ping-gai1,JI Tao1
(1.College of Electrical Engineering,Anhui Polytechnic University,Wuhu 241000,China;2.Department of Electrical Engineering,Anhui Technical College of Mechanical and Electrical Engineering,Wuhu 241000,China)
A fast median filtering algorithm was proposed to improve complex sorting and low efficiency in the Median filtering algorithm.First of all,the pixels of filter window were sorted by the order statistics theory.Based on this,the median of filter window was quickly found by using the relationship between the adjacent filtering window category information.And a new pair of pixels was migrated,while the ordering information of the remaining column pixels was reserved.Finally,the results of contrast experiment were presented to verify the high efficiency of the proposed method.
filter window;median;comparison;algorithm
TP391
A
1672-2477(2016)04-0063-05
2016-01-10
国家自然科学基金资助项目(61203033)
马运强(1989-),男,安徽亳州人,硕士研究生.
魏利胜(1978-),男,安徽巢湖人,副教授,博士.
