基于ARIMA的NCS随机时延预测
2016-09-07安徽工程大学电气工程学院安徽芜湖241000
徐 旺,葛 愿,王 炎(安徽工程大学电气工程学院,安徽芜湖 241000)
基于ARIMA的NCS随机时延预测
徐旺,葛愿∗,王炎
(安徽工程大学电气工程学院,安徽芜湖241000)
提出一种基于自回归求和滑动平均(Autoregressive Intergrated Moving Average,ARIMA)模型预测网络化控制系统(Networked Control System,NCS)随机时延的方法,对随机时延序列进行数据预处理,建立模型进行预测,同时进行了理论推导和仿真实验.结果表明,采用ARIMA模型可对NCS随机时延准确预测,并与基于ARMA模型的预测结果进行比较,预测精度得到了提高.
NCS随机时延;自回归求和滑动平均;时延预测
随着互联网的迅速发展,网络和控制系统的结合逐渐成为研究的热点.其中,关于网络化控制系统(Networked Control System,NCS)的研究已经成为当前自动化领域中的一个前言课题.网络化控制系统是一种通过传感器、控制器和执行器之间数据交换的分布式实时反馈控制系统,具有安装简单、系统可靠、远程控制等优点.控制系统引入网络后,其性能将因网络时延的存在而受到影响[1-3].网络时延成为影响网络化控制系统性能的一个主要因素,故准确预测网络时延有助于提升网络化控制系统的性能.
基于现有的研究发现,针对网络化控制系统时延预测主要有以下几个大方向:基于回归建模预测方法[4-5],其需要对模型精确建模,其模型参数的求解过程复杂,很难在线递推;基于神经网络预测方法[6],其存在易于陷入局部最优值以及过分依赖输入时延序列的自相关系数的问题;基于支持向量机预测方法[7],其预测算法的参数很难确定.
由于网络化控制系统随机时延预测对预测精度和速度都有较高的要求,上述预测方法或多或少存在各类不足.因此,采用自回归求和滑动平均模型(Autoregressive Intergrated Moving Average,ARIMA)[8],对网络化控制系统随机时延进行预测.将通过Opnet搭建的网络化控制系统测得的随机时延序列视为一个时间序列,用ARIMA模型来近似拟合该时间序列.当模型拟合成功后,就可以从该时间序列的过去值及现在值来预测未来的时间序列值.
1 随机时延的ARIMA模型
网络化控制系统的一般结构如图1所示.由图1可知,网络化控制系统随机时延主要包括前向通道网络时延和后向通道网络时延.控制器到执行器的传输时延称为前向通道网络时延,记第k个采样周期的前向时延为;传感器到控制器的传输时延称为后向网络通道时延,记第k个采样周期的后向时延为.因可以通过时间戳计算出来,故文中网络化控制系统随机时延即为.记网络化控制系统在第k个采样周期t内获得的随机时延序列为一个长度为k-1的时间序列,而此时还未发生,故需要对进行预测.若对进行d次差分得到一个平稳的ARM A模型,则称为自回归求和滑动平均ARIMA模型.其中,AR是自回归,p为自回归项,表示一个数与前面几个数线性相关;MA为移动平均,q为移动平均项数,表示平滑计算的次数;d为差分,描述长期趋势.
1.1AR(p)模型
AR过程是通过过去观测值的残差包含在现在观测值的回归模型中,以AR(1)位特例实现随机误差项的一阶自相关过程:
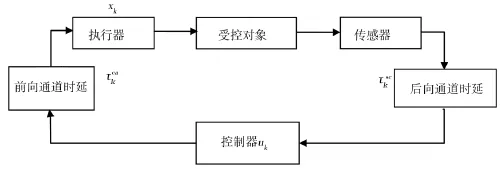
图1 网络化控制系统的一般结构

在回归分析的基础上,通过交换变形为非线性方程如式(3),并通过Marquardt非线性最小二乘估计ρ、β:

(1)滞后阶数的确定.通过AIC规则来实现模型滞后阶数的确定:

其中,L为时间序列自身的似然函数.
(2)模型预测值.

1.2MA(q)模型
(1)模型结构.
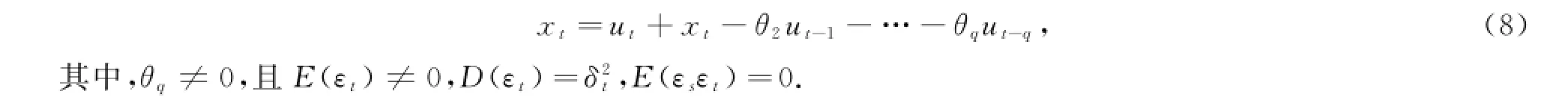
(2)滞后阶数的确定.通过ACF截尾特征来实现模型阶数的确定:

1.3ARMA(p,q)模型
其表达式如下:

ARMA模型是AR自回归模型与MA移动模型的结合,结合AR与MA模型的滞后项判断法就可直接判断出ARMA(p,q)值.
通过网络化控制系统的随机时延数据特征已经证实,随机时延时间序列在一阶、二阶差分条件下平稳,由此ARMA模型可扩展为ARIMA(p,d,q)模型,其中,d=1表示一阶差分;d=2表示二阶差分.
2 基于Opnet的NCS随机时延仿真
文中所需网络化控制系统随机时延序列是通过Opnet软件搭建的网络模型(见图2)获取的.在不同的节点之间进行信息传输,节点发包速率设置为50个/s,数据包大小设置为188 bits,网络仿真时间设置为200 0 s.网络中源节点source和目标节点end之间通过3个交换节点相连.
测试中,源节点source通过网络向目标节点end发送数据包,经过多次测试,获得了大量的随机时延序列.测试得到的source-end接发包随机时延序列如图3所示.

图2 NCS中source发包end收包
3 基于ARIMA模型的随机时延预测
3.1基于ARIMA模型的随机时延拟合
使用仿真软件SPSS对图3进行ARIMA模型建模、预测,针对测试得到的随机时延序列,提取150 0个用于该仿真实验.将前100 0个随机时延序列作为训练数据,用于参数估计及模型的建立;后500个随机时延序列作为预测数据,用来检测预测值与实际值的差距.
通过一阶差分对所提取的前100 0个训练数据的平稳化处理结果如图4、图5所示.从图4、图5可以看出,经过处理后数据的自相关函数无显著地异于零,其偏相关函数也是如此.故参数d取值1.此处,令p=1,q=1,则可得到拟合数据如图6所示.从图6可以看出,ARIMA(p=1,d=1,q=1)模型能很好地拟合随机时延,可以满足接下来的预测要求.

图3 source-end接发包随机时延序列
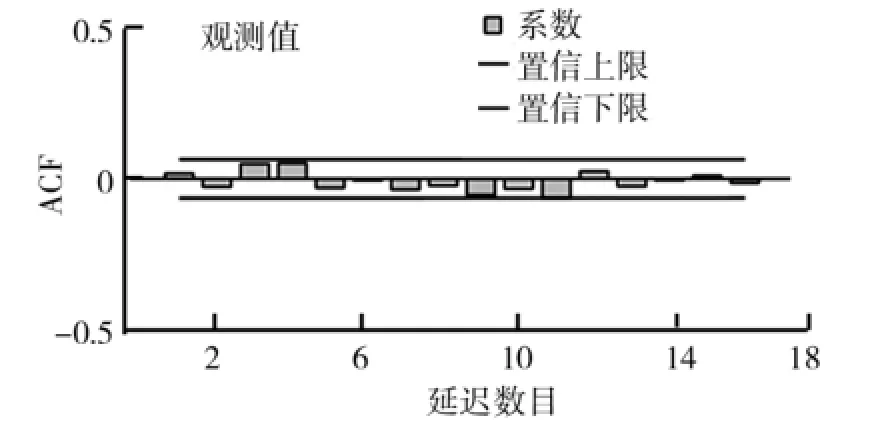
图4 随机时延序列一阶差分自相关(ACF)
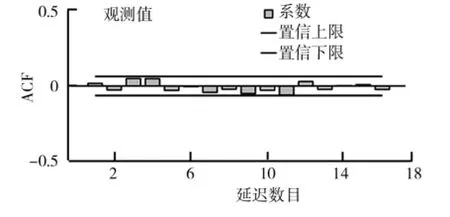
图5 随机时延序列一阶差分偏相关(PACF)
通过二阶差分对所提取的前100 0个训练数据的平稳化处理结果如图7、图8所示.从图7、图8可以看出,经过处理后数据的自相关函数无显著地异于零,其偏相关函数也是如此.因此参数d取值为2.此处,令p=1、q=1,则可得到拟合数据如图9所示.从图9可以看出,ARIMA(p=1,d=2,q=1)模型能很好地拟合随机时延,可以满足接下来的预测要求.

图6 随机时延拟合图(p=1,d=1,q=1)

图7 随机时延序列二阶差分自相关(ACF)

图8 随机时延序列二阶差分偏相关(PACF)
3.2预测结果及分析
利用建立的ARIMA模型对NCS随机时延序列进行预测,一阶差分(d=1)、二阶差分(d=2)及基于ARM A模型的预测结果分别如图10、图11及图12所示.

图9 随机时延拟合图(p=1,d=2,q=1)
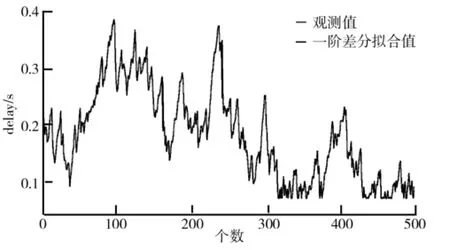
图10 观测值及一阶差分预测值
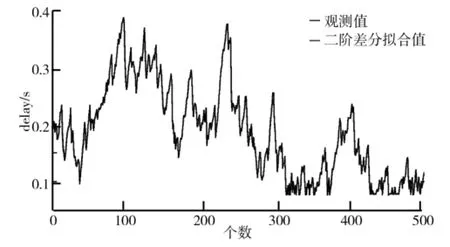
图11 观测值及二阶差分预测值
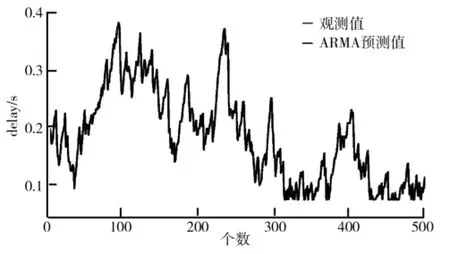
图12 观测值及ARM A预测值

采用均方误差(Mean Squared Error,MSE)来评判预测结果的优劣,设均方误差MSE的值为M,即式中,n表示随机时延序列的个数;^x(i)为随机时延序列预测的第i个的值;x(i)为实际随机时延序列的第i个的值.根据图10、图11、图12通过计算得到M值如表1所示.由表1可知,基于ARIM A方法对网络化控制系统的随机时延序列预测的结果与基于ARM A方法预测的结果相比,精度得到了很大地提高.相较基于ARIMA方法自身,二阶差分后的预测精度比一阶差分后的预测精度更高.预测结果与真实值相差很小,可以满足预测要求.

表1 预测结果比较
4 结束语
基于网络化控制系统随机时延的随机性很强,且NCS随机时延具有非平稳性.通过差分对随机时延序列进行平稳化处理,然后根据ARIMA模型中参数确定的要求,得到能够很好拟合随机时延序列的ARIMA模型,进而对随机时延序列进行预测.仿真实验表明,预测精度得到了提高.
[1]K Kosuge,T Itoh,T Fukuda.Scale Telemainpulation with Communication Time Delay[C]//Processing of 1996 IEEE International Conference on Robotics and Automation Minneapolis,Minnesota,USA:IEEE Press,1996:2 019-2 024.
[2]G Niemeyer,J J E Slotine.Towards Force-reflecting Teleoperation over Internet[C]//Processing of the IEEE International Conference of Robotics an Automation,Belgium,Leuven:IEEE Press,1998:1 909-1 915.
[3]Goldberg K,Chen B,Solomon R,et al,Collaborative Teleoperation Via The Internet[C]//IEEE Internation Conference on Robotics and Automation,San Francisco,California:IEEE Press,2000:2 019-2 024.
[4]宋杨,涂小敏,费敏锐.基于FARIMA模型的Internet时延预测[J].仪器仪表学报,2012,33(4):757-763.
[5]N Sadeghzaedh,A Afshar,M B Menhaj.An MLP Neural Network for Time Delay Prediction in Networked Control Systems[C]//2008 Chinese Control and Decision Conference,China:IEEE Press,2008:5 314-5 318.
[6]曹庆璞,董淑福,罗骞.网络时延的混沌特性分析及预测[J].计算机技术与发展,2010,20(4):43-46.
[7]X H Fu,X Fu.A Predictive Algorithm for Time Delay Internet Network[C]//IEEE International Conference on Electronics,Communications and Control,China:IEEE Press,2011:666-669.
[8]G E P Box,G M Jenkins.Time Series Analysis Forecasting and Control[M].San Francisco:Holders Day,1976.
Predicting NCSStochastic Delay Based on ARIMA
XU Wang,GE Yuan∗,WANG Yan
(College of Electrical Engineering,Anhui Polytechnic University,Wuhu 241000,China)
A novel method based on ARIMA(Autoregressive Intergrated Moving Average)was proposed for forecasting NCS(Networked control system)stochastic delay,the data preprocessing.The model are established to predict the random time delay series,theoretical and simulation verification are carried out.The results demonstrate that the NCS stochastic delay fitted by ARIMA can be modeled and predicted well.Compared with the prediction results based on ARMA model,the prediction precision was improved.
NCS stochastic delay;ARIMA;delay forecasting
TP13
A
1672-2477(2016)04-0072-05
2016-02-24
安徽省自然科学基金资助项目(1308085QF120)
徐旺(1991-),男,安徽宣城人,硕士研究生.
葛愿(1979-),男,江苏徐州人,教授,博士.
