基于事件触发的网络控制系统稳定性分析
2016-09-07李迎迎安徽工程大学电气工程学院安徽芜湖241000
李迎迎,江 明(安徽工程大学电气工程学院,安徽芜湖 241000)
基于事件触发的网络控制系统稳定性分析
李迎迎,江明∗
(安徽工程大学电气工程学院,安徽芜湖241000)
针对具有时变时滞的网络控制系统模型,设计一个事件触发条件.运用Lyapunov泛函和线性矩阵不等式知识进行稳定性分析,最后用一个数值例子进行Matlab仿真,验证了设计方法的有效性.
网络控制系统;时变时延;事件触发机制;Lyapunov泛函;线性矩阵不等式
网络控制系统(Networked Control Systems,NCSs)是一种空间分布式系统[1],被控对象、传感器、控制器和执行器由一个有限带宽的通信网络连接.将网络引入到控制系统当中,所带来的最突出的问题是网络时延和带宽受限.虽然传统的周期采样方式易于实现,但从资源利用的角度来看,这种方式已经不适用.因为当系统在理想的状况下运行且周期性地执行任务时,会造成资源和带宽的浪费.随着系统规模的不断增大,网络传输的数据量越来越大,从减少对有限的网络带宽资源的浪费和提高资源利用率两个方面研究NCSs,使得基于事件触发机制的NCSs的研究得到越来越多的关注.迄今为止,M.D.Lemmon[2]和Paulo Tabuada[3]在等事件触发机制方面取得了显著成果.在国内,有关事件触发机制的研究刚起步,有少量文献报道[4-5].考虑到有些系统的状态不易测量,设计了一个基于输出的事件触发机制来控制采样器采样信号的发送.首先,对具有时变时滞的NCSs系统进行建模;然后运用Lyapunov稳定性理论以及线性矩阵不等式(Linear Matrix Inequality,LMI)方法,研究基于事件触发机制的NCSs的稳定性问题;最后通过仿真实例,验证文中方法的有效性.
1 问题描述
基于事件触发机制并具有时变时延的网络控制系统结构如图1所示.考虑如下形式的一个被控物理对象为:

式中,x(t)∈Rn是系统状态向量;u(t)∈Rm是控制输入;ω(t)∈Rp是外部干扰,且ω(t)∈L2[0,∞);y(t)∈Rp为输出向量;A、B、Bω和C是相应维数的参数矩阵.由图1可以看出,τsc是传感器到控制器的时延,τca是控制器到执行器的时延.假设控制器的计算时延可忽略不计,定义τk=τsc+τca为整个网络时延,系统的初始化条件为x(t0)=x0.假设式(1)通过一个带有网络输出反馈控制器u(t)=Ky(t)的通信网络来完成控制任务,控制器直接通过一个零阶保持器(ZOH)连接到执行器上.

图1 事件触发机制的网络控制系统模型
为了简化理论分析,做如下NCSs研究中常见的假设:通信网络中的传感器都是以固定的采样周期h时间触发的,控制器和执行器是事件触发的;网络控制系统通信信道中的信号都是以单包形式传输的,且控制器的计算时延可忽略不计;总的诱导时延τk(k∈Z+)是有界的.0<τk<¯τ,其中,¯τ代表时延的上界.
考虑系统通信信道容量有限,为减少网络中数据传输的个数,为NCSs被控对象设计一个输出依赖型事件触发机制.如下:

式中,y((k+j)h)是当前输出采样数据;y(kh)是最近一次被成功传递出去的输出采样数据;V是一个正定矩阵,j∈Z+,σ∈[0,1).
满足式(2)的输出采样数据y((k+j)h)不会被传输到控制器端,只有不满足式(2)的采样数据才被发送到控制器端.很显然,这个事件触发机制将会降低网络中的通信负载.在特殊情况下,式(2)中取σ=0,则对几乎所有的采样输出数据y((k+j)h)式(2)都不成立,此时,事件触发机制将退化成时间触发机制.
在事件触发机制即式(2)下,假设采样输出释放时刻为t0h,t1h,t2h,….其中,t0h是初始释放时刻;γk=tk+1h-tkh定义为事件触发机制下的传输周期.考虑到网络信道中的时变时延τk,这些释放输出信号将分别在t0h+τ0,t1h+τ1,t2h+τ2,…时到达控制器端.

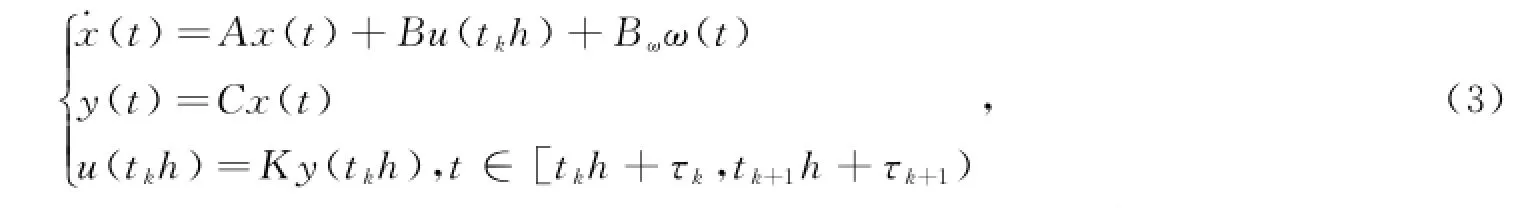
第一种情况,若tk+h+¯τ≥tk+1h+τk+1,定义一个函数:

明显的,

相应地,定义一个误差向量:

第二种情况,若tk+h+¯τ<tk+1h+τk+1,考虑如下区间

由于τk<¯τ,不难得到存在dM满足不满足式(2)则不被发送到控制器.

定义函数:
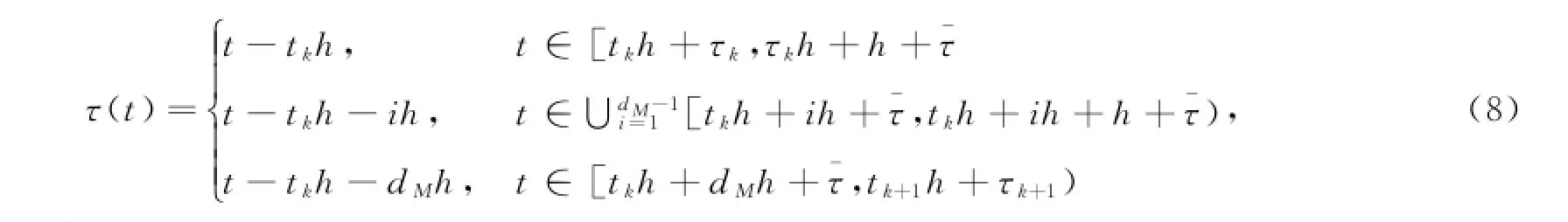
由式(8)可知:

定义误差函数:

结合式(2)、式(6)和式(10),可以得出:

结合式(3)、式(4)、式(6)、式(8)和式(10),当t∈[tkh+τk,tk+1h+τk+1)时,基于事件触发机制的NCSs的模型为:

其中,ψ(t)定义为x(t)的初始化函数.
引理1(Wirtinger不等式)给定一个矩阵G>0,对于连续函数ω∈Rn在区间[a,b]上有下列不等式成立[6]:

定义1如果下列两个条件同时满足,则称闭环系统渐进稳定且H∞扰动抑制水平为γ.
(a)式(12)在ω(t)=0时是渐进稳定的;
(b)在零初始条件下,对任何非零的ω(t)∈L2[0,∞)和一个给定的γ>0,有‖y(t)‖2<γ‖ω(t)‖2.
2 主要结论
当系统中不存在扰动,即ω(t)=0时,研究式(12)的稳定性问题,首先给出如下稳定性条件.
定理1对于一些给定的参数σ和反馈增益K,在事件触发机制即式(2)的条件下,如果存在合适维数的实矩阵P>0,Q>0,R>0和V>0满足下列线性矩阵不等式:

那么式(12)是渐进稳定的.

证明构建如下形式的Lyapunov-krasovskii泛函:

其中,P=PT>0,Q=QT>0,R=RT>0.在t∈[tkh+τk,tk+1h+τk+1)范围内,沿着式(12)对V(t)进行求导,同时加上和减去eTk(t)Vek(t)这一项,可得:
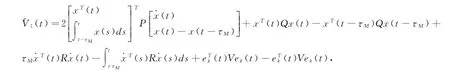

整理后得

式(14)Π<0保证了̇V(t)<0.由Lyapunov稳定性理论,当ω(t)=0时,式(12)是渐近稳定的,即满足条件(a).
证毕.
考虑系统中存在扰动的情况,即ω(t)≠0时,给出如下定理.
定理2对于给定的参数σ,γ>0和反馈增益K,在事件触发机制,即式(2)的条件下,如果存在合适维数的实矩阵P>0,Q>0,R>0和V>0满足下列线性矩阵不等式:

构造形如式(15)的Lyapunov-krasovskii泛函,进行类似证明定理1时对泛函导数的处理可得:

通过对比可知,式(17)等价于Ψ<0,从而

式(19)两边对t从0到∞积分,有:

在零初始条件下,有V(0,x0)=0,而V(∞,x∞)≥0,于是式(20)成立

证毕.
3 仿真实例
考虑具有如下参数的系统(1),其参数如下:

取σ=0.2,γ=2,控制器增益K=[0.10.2].根据定理2,运用Matlab中的LMI工具箱[7]求解线性矩阵不等式(17),经过迭代运算,可以得到τM的上界为0.615 1,相应的事件触发矩阵为:

假设τk≡0,τM=h+¯τ,最大采样周期h为0.615 1.γ反映了系统对外部扰动的抑制能力,γ越小,表明系统的性能越好.
4 结论
考虑到网络通信带宽资源的有限性,为了减小NCSs中通信信道的网络负载,节约网络带宽资源,提出了一种新的事件触发条件来控制采样信号是否在通信网络中被传输到控制器端.基于时变时滞系统模型,讨论了一类线性网络控制系统的一致有界稳定性问题.最后的例子表明:运用提出的事件触发机制,在保证闭环系统稳定的前提下,能够有效地减少网络中的数据传输量,进而降低网络负载压力,节约了网络带宽资源.由于没有考虑数据包丢失以及多包传输等问题的影响,所建模型较为理想化,因此,要应用于实际的网络控制系统,还有待进一步深入研究.
[1]岳东,彭晨,Q L Han.网络控制系统的分析与综合[M].北京:科学出版社,2007.
[2]X Wang,M D Lemmon.Self-triggered Feedback Control Systems with Finite-Gain L2Stability[J].IEEE Transactions on Automatic Control,2009,54(3):452-467.
[3]M Mazo Jr,A Anta,P Tabuada.An ISS Self-triggered Implementation of Linear Controllers[J].Automatica,2010,46(8):1 310-1 314.
[4]严胜.基于事件触发的网络控制系统控制与滤波[D].上海:华东理工大学,2014.
[5]张进.基于事件传送策略的网络化控制系统协作控制研究[D].南京:南京师范大学,2014.
[6]A Seuret,F Gouaisbaut.Wirtinger-based Integral Inequality:Application to Time-delay Systems[J].Automatica,2013,49(9):2 860-2 866.
[7]俞立.鲁棒控制-线性矩阵不等式处理方法[M].北京:清华大学出版社,2002.
Stability Analysis of Event-triggered Control for Networked Control
LI Ying-ying,JIANG Ming∗
(College of Electrical Engineering,Anhui Polytechnic University,Wuhu 241000,China)
Networked control systems with time-varying delay was discussed and an event-triggered condition was designed.Then,system stability was analyzed by using Lyapunov function and linear matrix inequality.A numerical example was given to demonstrate the effectiveness by Matlab simulation in the end.
networked control systems;time-varying delay;event-triggered scheme;lyapunov function;linear matrix inequality
TP273
A
1672-2477(2016)04-0077-06
2016-01-10
国家自然科学基金资助项目(61271377)
李迎迎(1987-),女,安徽宿州人,硕士研究生.
江明(1965-),男,安徽芜湖人,教授,硕导.
