Multi-scale morphology analysis of acoustic emission signal and quantitative diagnosis for bearing fault

Wen-Jing Wang·Ling-Li Cui·Dao-Yun Chen



Multi-scale morphology analysis of acoustic emission signal and quantitative diagnosis for bearing fault

Wen-Jing Wang1·Ling-Li Cui2·Dao-Yun Chen1

©The Chinese Society of Theoretical and Applied Mechanics;Institute of Mechanics,Chinese Academy of Sciences and Springer-Verlag Berlin Heidelberg 2015

AbstractMonitoring of potential bearing faults in operation is of critical importance to safe operation of high speed trains.One of the major challenges is how to differentiate relevant signals to operational conditions of bearings from noises emitted from the surrounding environment.In this work,we report a procedure for analyzing acoustic emission signals collected from rolling bearings for diagnosis of bearing health conditions by examining their morphological pattern spectrum（MPS）through a multi-scale morphology analysis procedure.The results show that acoustic emission signals resulted from a given type of bearing faults share rather similar MPS curves.Further examinations in terms of sample entropy and Lempel-Ziv complexity of MPS curves suggestthatthesetwoparameterscanbeutilizedtodetermine damage modes.

KeywordsBearingfault·Acousticemission·Morphological pattern spectrum（MPS）·Sample entropy·Lempel-Ziv complexity

1　Introduction

A bearing is one of the most common transmission parts of mechanical equipment.Bearing fault diagnosis plays a significan role in the safety and reliable operation of the equipment,especially in high speed train operation［1］.As is well established,during an early stage of bearing failure,characteristic signals resulting from a fault are typically very weak and may not distinguishable from surrounding noises.Hence,itisdifficul tofin ameaningfulprecursorfor potential failure using the traditional vibration signal identificatio methods.Acousticemissionbasedonthemonitoring method,because of its advantages in the weak signal detection,has attracted increasing attention and has been applied for the bearing safety monitoring and the fault diagnosis.In addition,Forjani and Mba［2］proved by their experimental study that the acoustic emission method could effectively detect the crack propagation in low speed running of a bearing.They also pointed out that the energy parameters of the acoustic emission signals play a very important role in fault differentiation in the rolling bearings.In their study, Al-Ghamdetal.［3］comparativelystudiedtheacousticemission signals and vibration signals of ball bearing outer ring faults on a test bench.They concluded that the effective value,the maximum amplitude,and the kurtosis value of the acousticemissionsignalsaremoresensitivethanthoseofthe vibration signals.As a result of the aforementioned advantages,acoustic emission signals have been widely used for the rolling bearing fault diagnosis.Since the acoustic emission signals caused by faulty bearings are non-stationary, a mathematical morphology is adopted for the fault identification There exist some successful fault diagnosis cases studied by applying the mathematical morphology method in processing the vibration signals［4-7］.Introduction of the morphologicalanalysismethodinprocessingandanalysisof one-dimensional signals for the fault diagnosis was done by Zhang［4］.Then,Wang et al.［8］proposed an adaptive generalized morphological filte method in the medium’s data processingforonlinemonitoring.Inaddition,Zhangetal.［9］appliedthemorphologicalfilte methodtothenoisereduction of vibration signals and achieved promising results.Fourth, Lu et al.［10］studied adaptive noise reduction of multiscale and multi-element morphological filte.Fifth,Hao et al.［6］used a morphological filte method for analyzing the rollingbearingacousticemissionsignalsforthenoisereduction and signal enhancement.Their results have shown that the effect was striking when the morphological filte was used in the processing acoustic emission signals and feature extraction,demonstrating that their proposed method was suitable for monitoring bearing condition and early diagnosing the fault.Sixth,Li et al.［11］put forward a noise reduction method of the low speed rolling bearing acoustic emission signals based on a morphological filte technique in the frequency domain,which has also achieved an effective noise reduction.Lastly,Dong et al.［12］put forward an adaptive morphological filte method that was based on the energy ratio with which an effective noise reduction was documented.

It is worth pointing out that the signal analysis method usedbyaforementionedresearcherscanbecharacterizedasa single scale morphology filte technique,rather than a multiscale morphology method.To address such a deficien y,a mathematical pattern spectrum,also known as a magnitude histogram of morphologic characteristics,was developed based on the multi-scale morphology.It is a method of shape representation in image analysis and can be used to describe object shape image and extract shape features［13］.It was appliedbyHao［14］tothemulti-scalemorphologyanalysisto faultsignalanalysisofarollingbearing.Thepatternspectrum from multi-scale morphology analysis can reflec morphological variation characteristics under different scales.Also, Yu et al.［15］combined the pattern spectrum with a support vector machine to realize quantitative diagnosis of faults. Application of a support vector machine was done by Hao et al.［16］,which was based on pattern spectrum entropy,into fault diagnosis of rolling bearing.Another contribution was byZhangetal.［17］whoputforwardrotatingthemachinery’s fault diagnosis method,which was based on the combination of local mean decomposition and morphological pattern spectrum（MPS）.So far,the strength of MPS for analysis of vibration signals has been widely recognized in the fault diagnosis of rotating machinery.The focus of this work is to examine critically the applicability of MPS to acoustic emission signals for identifying possible damage in bearings—a topic that has received little attention until recently.We firs introduce the concept of multi-scale morphology and MPS, then apply the method for extracting important characteristics of acoustic emission signals.A quantitative diagnosis of fault bearing acoustic emission signals by using sample entropy and complexity respectively is then carried out,and verifie by experiments based on the acoustic emission signals of bearings under different fault conditions.

2　Multi-scale morphology and MPS

The essential parts of morphology theory involve the design andselectionofstructuralelements,morphologytransformation,and calculation procedures.Representative structural elements based on signal morphological characteristics are needed for performing morphology transformation of original signals.The choice of such elements is crucial to determiningwhetherthetransformedsignalsinheritthelocal features of the original signals.The multi-scale method as suggested by Matheron’s Random Sets and Integral Geometry,using openings and closings to obtain probabilistic size distributions of continuous binary images,is regarded as a shape-size descriptor.We can construct a MPS of arbitrary multilevel signals that reflect the shape-size information of the signals,i.e.,（or e.g.,）large impulses in the MPS at a certain scale corresponding to major substructures of the signal at that scale［13］.Therefore,MPS curves can be used to deduce distribution features of different characteristic components from signals such as noise component or impact component［14］.The readers are referred to the publication byMaragos［13］fornumericaldetailsabouthowtoconstruct MPS of discrete signals.

Set f（x）as a non-negative function,x∈Rm,m= 1,2,...,M−1,in which M is a natural number and here it is the gray level of image.Set g（x）as a convex function.So the MPS of f（x）can be define as

The formula（1）is for the open operation MPS and formula （2）is for the closed operation MPS. For a discrete signal,MPS can be define as

3　Acoustic emission signal analysis of bearings on test rig

In order to examine whether the MPS obtained by the multiscale morphology can be applied to the acoustic emissionsignals from bearings,we designed a rolling bearing testing system,with the layout diagram shown in Fig.1.Here the component marked by1○represented the three-phase induction motor,which drives shaft rotation through belt transmission,and2○,3○,and4○arebearingseats.TwoN205 rolling bearings were installed on3○and4○.The bearing in good condition was installed on3○and a bearing with a simulated fault was installed on4○.The motor speed was 1060 r/min in the test.The bearing’s outer ring,inner ring, and rolling body were cut artificiall through wire cutting to simulatecrackfaults.Thecrackwidthis1mm,with2mmin depth.Theacousticemissionsensorwasfi edto4○.Acoustic emission data were collected by using of the acoustic emission acquisition system and computers.Sampling frequency was set at 800 kHz with total sampling points of 262144.

Fig.1 The bearing test rig.Here1○is a three-phase induction motor, and2○,3○,and4○are bearing seats.Two N205 rolling bearings,with one in good condition and the other being cracked,were installed at3○and4○,respectively

Wecollectedsignalsofbearingswithdifferentfaults,outer ringcrack,innerringcrack,androllingbodycrack.Thetime historychangesofthesignalsareshownfromFigs.2a,3,and 4a respectively.For comparison purposes,the signals from the bearing in good condition were also given out in Fig.5. Although we can tell differences of the signals between the bearing in good condition and those in cracked status,it is not straightforward to determine crack locations.We then resort to examining MPS curves derived from time-history signals,as detained in Figs.2b,3,4,and 5b,corresponding to bearings with outer ring crack,inner ring crack,rolling body crack,and in good condition.There are two important observations here:

（1）The MPS curves of the same kind of fault signals have consistent shapes and trends.The maximum amplitudes from each fault signal happened on the same structural element scale.A good reliability of the MPS analysis is verified

（2）The peaks and detailed shape of MPS curves of bearings in different fault conditions are distinct,which can be used for bearing fault diagnosis.

Fig.2　a Time domain waveform.b Morphological pattern spectrum. Time-domain graph and MPS of three outer ring crack fault signals

For convenience,we plot the MPS of bearings with outer ring cracking,inner ring cracking,rolling body cracking, and intact conditions in Fig.6.The MPS value of the bearing in good condition reaches the maximum at about scale 20,however,the MPS values of the defective bearings reach the maximum at about scale 8.It indicates that the signal feature information,which matched with structural elements at scale 8,is dominant;the MPS values of outer ring cracks and inner ring cracks are greater than that of the bearing in good condition.The frequency sequence of outer ring fault frequency fo,inner ring fault frequency fi,and rolling body fault frequency fbfollows

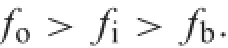
That means the most impacts happened on the outer ring fault.Its MPS has the maximum value in the low scale and decreasesfastatthehighscale.TheMPSvaluesofinnerring fault bearing and rolling body fault bearing drop moderately with the scale increasing.

Fig.3　a Time domain waveform.b Morphological pattern spectrum. Time-domain graph and MPS of three inner ring crack fault signals

4　Quantitative descriptions of MPS

Althoughthedistributionfeaturesofcomponentsignals’different components can be judged from the whole features of MPS curves,then from this the bearing fault characters can be deduced.This method can be further improved by recognizing the fact that the shape of the MPS curves of defective bearings is similar.For quantitative fault diagnosis ofrotatingmachineries,entropyandcomplexityaretwocommonly used methods.Based on sample entropy of a wavelet packet,Wang et al.［18］put forward the rolling bearing’s fault feature extraction method,calculated sample entropy of the reconstructed signals,and applied the sample entropy toassessfaultstate.Inaddition,Zhaoetal.［19,20］performed a combined envelope sample entropy of model function component with a support vector machine,which was successfully applied for bearing fault diagnosis.In addition to entropy information,the Lempel-Ziv complexity reflect the complexity of signal sequence,and it was also applied in faultdiagnosis.Thentoo,Hongetal.［21］combinedLempel-Zivcomplexitywithacontinuouswavelettransform,studied bearing inner and outer ring’s degree of damage,and effectivelyobservedthedamagetrend.Moreresearchwasdoneby Zhang et al.［22］putting forward research about the degree of rolling bearing’s fault damage that was based on empirical mode decomposition（EMD）and Lempel-Ziv index and achieved good results.Also,Wang et al.［23］put forward a kindofimprovedcomplexitybasedontime-frequencyanalysis,which was used in bearing fault diagnosis and achieved good results.It is clear that a quantitative diagnosis method of sample entropy and complexity has been shown to offer a great promise in fault bearing vibration signals research. However,itsapplicationinprocessingacousticemissionsignals is still a subject of intensive research.We now examine whether sample entropy and Lempel-Ziv complexity can be applied,based on the MPS information discussed in the previoussection,forfacilitatingbearingfaultidentification The flw chart is shown in Fig.7.

Fig.4　a Time domain waveform.b Morphological pattern spectrum. Time-domain graph and MPS of three rolling crack fault signals

Fig.5　a Time-domain waveform.b Morphological pattern spectrum. Time-domain graph and MPS of three normal bearing signals

4.1Sample entropy

For completeness,we firs discuss brieflthe algorithm description of sample entropy［24,25］.Let original data be {u（i）,i=1,2,...,N},the value of dimension m and similarity tolerance r is given in advance.Approximate entropy can be calculated as follows

（1）Arrangethesequence{u（i）}toformthem-dimensional

vector X（i）,that is

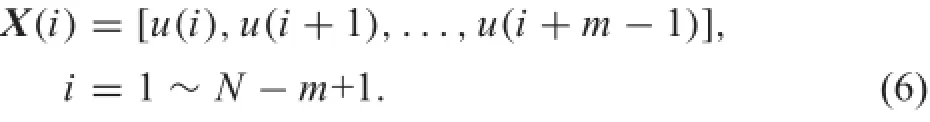
（2）Calculate the distance between vector X（i）and X（j）

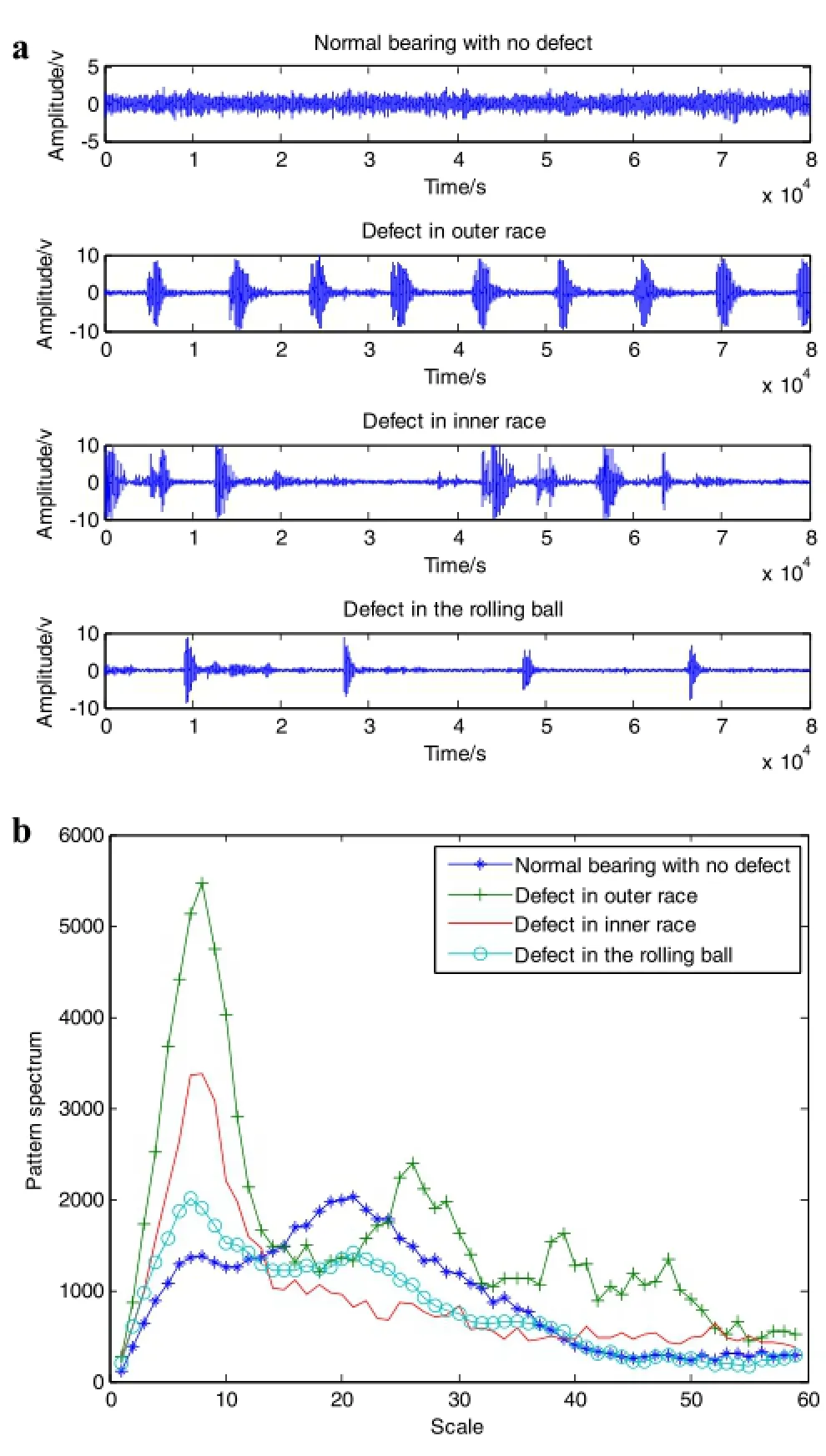
Fig.6　a Time-domain waveform.b Morphological pattern spectrum. Time-domain graph and MPS of three-type crack fault signals and the normal bearing signal

（3）According to the given threshold r（r＞0）,statistically the number of d［X（i）,X（j）］＜r for each i,which is called the template matching number,and the ratio of this number and N−m+1,which is denoted by Cmi（r）are

（4）Calculate the mean of Cmi（r）for all of the i,which is denoted by Φm（r）

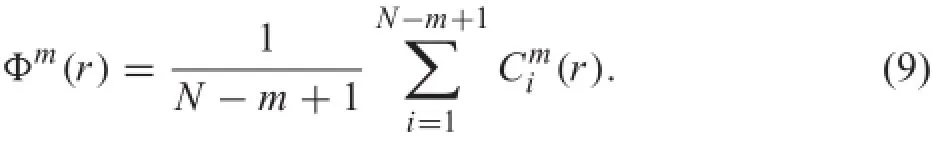
Fig.7　The flw chart of multi-scale morphological transform

（

（56））FI n o rt h m eo+ry,1t,hree pseaamt pElqes e.n（t1r）o-p（y4 ）ot fo t hgiest sΦeq mu +e 1n（c re） is

In fact,N can not be∞.When Nis a limited value, according to above steps,the result is sample entropy that can be approximated as

4.2Lempel-Ziv complexity

Lempel and Ziv introduced an easily calculable measure of complexity of finitsequences.Consider a string X（n）,firstlmaking binary conversion to X（n）,that is if X（i）≥mean（X（n））（i=1,2,···,n）,definS（i）= 1（i=1,2,...,n）,if not S（i）=0,getting S（n）= {s1,s2,...,sn},the Lempel-Ziv index of S（n）can be calculated through the cycle.

TheLempel-Zivcomplexityalgorithmcanbedividedinto the following two steps:

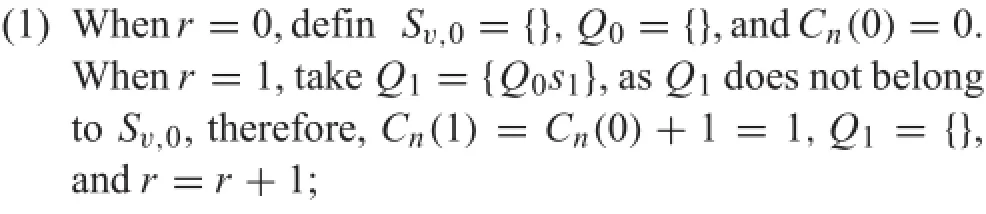
4.3Quantitative description result of the sample entropy

According to calculation formula of the sample entropy,this paper calculated six groups of MPS entropy of three types of fault bearings and the normal bearing as well.The results are listed in Table 1.Figure 8 is a graphical representation of Table 1.It can be seen that morphological spectrum entropy of different fault signals is clearly distinguished.This suggests that the morphological spectrum entropy can be used as a quantitative representation of fault types.

The value of morphological spectrum entropy can reflec the complexity of the MPS curves and the bigger the MPSentropy the more complex the acoustic emission signal sequence.Itcanbeseenthatmorphologicalspectrumentropy ofdifferentfaultsignalsisclearlydistinguishedfromthenormal bearing signals.This suggests that the morphological spectrum entropy can be used as a quantitative representation of fault types.

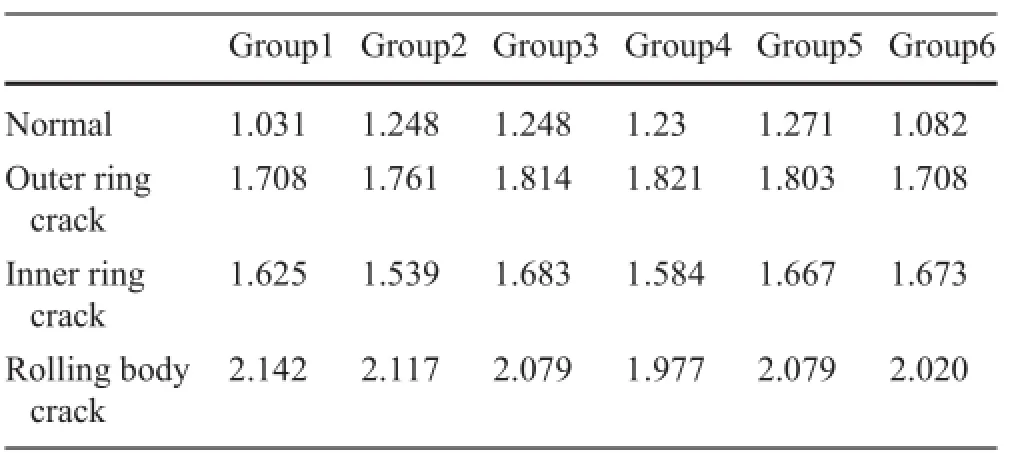
Table 1　The MPS entropy of three-type fault signals and the normal bearing signal

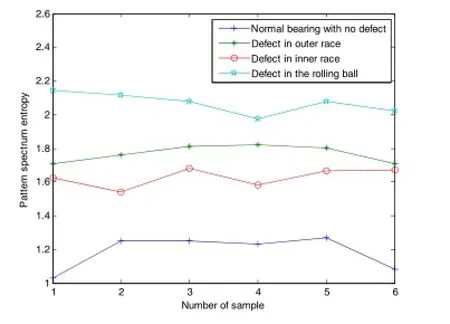
Fig.8　The MPS entropy of three-type fault signals and the normal bearing signal

4.4Quantitative description result of Lempel-Ziv complexity

Followingtheprocessofcomplexityalgorithm,weprocessed the acoustic emission signals of fault bearing and normal bearingwithoutdefect,andcalculatedsixgroupsofcomplexityforthem.TheresultsarelistedasTable2.Thecomplexity value of a signal sequence can reflec the frquency information of the signals.The greater complexity indicates more frequency components in signals.The bearing fault will increase the frequency components,which finallleads to the increase of complexity value.It can be seen from Fig.9 that complexity values of different signals are clearly distinguished.What is more,compared with sample entropy,the trend of complexity value is much more level and can realize the quantitative expression of fault types effectively.

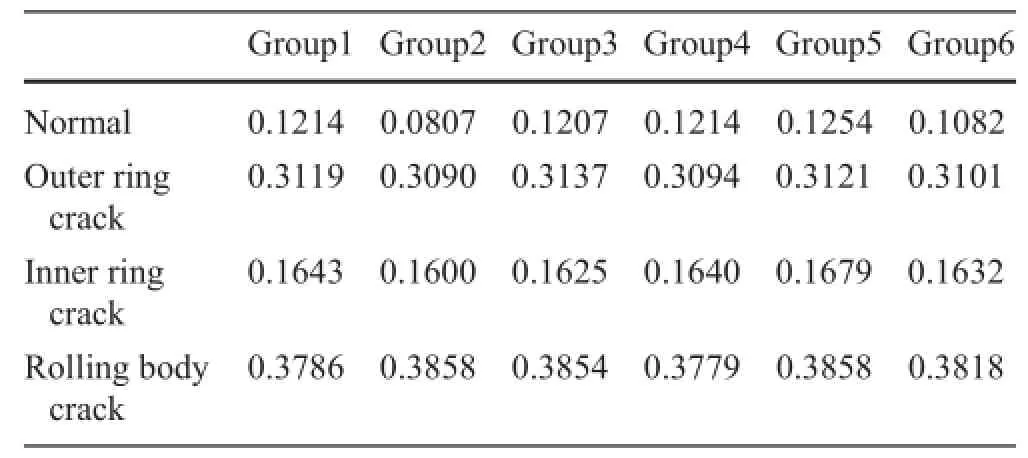
Table 2　The Lempel—Ziv complexity of three-type fault signals and normal bearing signal

Fig.9　The Lempel—Ziv complexity of three-type fault signals and normal bearing signal

5　Conclusions

In this study,we examined a bearing fault monitoring and diagnostic method by acoustic emission MPS obtained by the multi-scale morphology analysis.Sample entropy and Lempel—Ziv complexity in a MPS are adopted for sample identification The following conclusions can be drawn:

（1）Based on characteristic features of acoustic emission signals from bearing tests,we proposed a multi-scale morphological analysis method for extracting signal MPS,whichcanberelatedtoacousticemissionsignals’morphological variation characteristics under different scales.

（2）By simulating acoustic emission signals of both faulty bearings and bearings in the good condition through the rig tests,we have found that MPS curve of acoustic emission signals can be used to identify specifi fault types.The sample entropy and complexity of MPS can identify different types of bearing faults quantitatively, and a complexity parameter seems to serve as a rather stable indicator than the sample entropy under the same fault condition.Hence,we recommend the complexity tobeusedasaneffectiveindicator.Theworkprovidesan analysis method in processing fault bearing’s acoustic emission signals.

AcknowledgmentsThisworkwassupportedbytheNationalNatural Science Foundation of China（Grant 51205017）,the National Science and Technology Support Program（Grant 2015BAG12B01）and the National Basic Research Program of China（Grant 2015CB654805）.

References

1.Yang,G.W.,Wei,Y.J.,Zhao,G.L.,etal.:Currentresearchprogress inthemechanicsofhighspeedrails.Adv.Mech.45,201510（2015）

2.Elforjani,M.,Mba,D.:Natural mechanical degradation measurements in slow speed bearings.Eng.Fail.Anal.16,521-532（2009）

3.Al-Ghamda,A.M.,Mba,D.:A comparative experimental study on the use of acoustic emission and vibration analysis for bearing defect identificatio and estimation of defect size.Mech.Syst. Signal Process.20,1537-1571（2006）

4.Zhang,L.,Xu,J.,Yang,J.,et al.:Multiscale morphology analysis and its application to fault diagnosis.Mech.Syst.Signal Process. 22,597-610（2008）

5.Hu,A.,Tang,G.,An,L.:Denoisingtechnique forvibrationsignals of rotating machinery based on mathematical morphology filte. Chin.J.Mech.Eng.42,127-130（2006）

6.Hao,R.,Feng,Z.,Chu,F.:Morphology filter for analyzing roller bearingfaultusingacousticemissionsignalprocessing.J.Tsinghua Univ.5,812-815（2008）

7.Zuo,Y.,Wang,X.,Xu,X.:Application of degree of cyclostation to trend analysis of fault in generator sets.J.Vib.Meas.Diagn.29, 292-294（2009）

8.Wang,N.,Lv,F.,Liu,Y.,et al.:Study on application of adaptive generalized morphological filte in processing online monitoring tan&date.Proc.CSEE.24,161-165（2004）

9.Zhang,W.,Yang,C.,Zhou,X.:Applicationofmorphologyfilterin method in vibration signal denoising.J.Zhejiang Univ.（Eng.Sci.）43,2096-2099（2009）

10.Lu,Z.,Mi,D.,Xu,Z.:Research in application of multi-scale and multi-element morphological filterin in geomagnetic orientation. J.Hebei Univ.Sci.Technol.32,228-232（2011）

11.Li,X.,Yang,J.,Li,M.,et al.:A time-frequency filterin method based on generalized S transform and its application in machinery fault diagnosis.Appl.Mech.Mater.157,531-537（2012）

12.Dong,Y.,Liao,M.,Zhang,X.,et al.:Faults diagnosis of rolling elementbearingsbasedonmodifie morphologicalmethod.Mech. Syst.Signal Process.2–5,1276-1286（2011）

13.Maragos,P.:Patternspectrumandmulti-scaleshaperepresentation. IEEE Trans.Pattern Anal.Mach.Intell.11,701-716（1989）

14.Hao,R.,Lu,W.,Chu,F.:Multiscale morphological analysis on fault signals of rolling element bearing Chinese.J.Mech.Eng.44, 160-165（2008）

15.Yu,X.,Lu,W.,Chu,F.:Faultdiagnosticsbasedonpatternspectrum entropy and proximal support vector machine.Key Eng.Mater. 413,607-612（2009）

16.Hao,R.,Feng,Z.,Chu,F.:Application of support vector machine based on pattern spectrum entropy in fault diagnostics of bearings. In:prognostics&system health management conference（2010）

17.Zhang,K.,Cheng,J.,Yang,Y.:Rotatingmachinery fault diagnosis based on local mean decomposition and pattern spectrum.J.Vib. Shock 32,135-140（2013）

18.Wang,F.,Zhang,Y.,Zhang,B.,etal.:Applicationofwaveletpacket sampleentropyintheforecastofrollingelementbearingfaulttrend. International conference on multimedia and signal processing 12-16（2011）

19.Zhao,Z.,Yang,S.:Sampleentropy-basedrollerbearingfaultdiagnosis method.J.Vib.Shock 31,136-154（2012）

20.Zhu,K.,Song,X.,Xue,D.:Fault diagnosis of rolling bearings based on IMF envelope sample entropy and support vector machine.J.Inform.Comput.Sci.10,5189-5198（2013）

21.Hong,H.B.,Liang,M.:Fault severity assessment for rolling element bearings using the Lempel-Ziv complexity and continuous wavelet transform.J.Sound Vib.320,452-468（2009）

22.Zhang,C.,Chen,J.:Fault severity assessment for rolling element bearings based on LMD and Lempel-Ziv index.J.Vib.Shock.31, 77-82（2012）

23.Wang,J.,Cui,L.,Wang,H.,et al.:Improved complexity based on time-frequency analysis in bearing quantitative diagnosis.Adv. Mech.Eng.5,258506（2013）

24.Serra,J.:Image Analysis and Mathematical Morphology.Academic,New York（1982）

25.Richman,J.S.,Moorman,R.J.:Physiological time series analysis using approximate entropy and sample entropy.Am.J.Physiol. Heart Circ.Physiol.278,H2039-2049（2000）

26.Lempel,A.,Ziv,J.:On the complexity of finit sequences.IEEE Trans.Inf.Theory 22,75-81（1976）

30 April 2015/Revised:4 August 2015/Accepted:8 October 2015/Published online:17 November 2015

✉Wen-Jing Wang wjwang@bjtu.edu.cn

1School of Mechanical,Electronic and Control Engineering, Beijing Jiaotong University,Beijing 100044,China

2College of Mechanical Engineering and Applied Electronics Technology,Beijing University of Technology, Beijing 100124,China