Correcting the initialization of models with fractional derivatives via history-dependent conditions

Maolin Du·Zaihua Wang



Correcting the initialization of models with fractional derivatives via history-dependent conditions

Maolin Du1·Zaihua Wang2,3

©The Chinese Society of Theoretical and Applied Mechanics;Institute of Mechanics,Chinese Academy of Sciences and Springer-Verlag Berlin Heidelberg 2015

AbstractFractional differential equations are more and more used in modeling memory（history-dependent,nonlocal,or hereditary）phenomena.Conventional initial values of fractional differential equations are defineat a point, while recent works defin initial conditions over histories. We prove that the conventional initialization of fractional differential equations with a Riemann-Liouville derivative is wrong with a simple counter-example.The initial values were assumed to be arbitrarily given for a typical fractional differentialequation,butwefin oneofthesevaluescanonly be zero.We show that fractional differential equations are of infinit dimensions,and the initial conditions,initial histories,are define as functions over intervals.We obtain the equivalent integral equation for Caputo case.With a simple fractional model of materials,we illustrate that the recovery behavior is correct with the initial creep history,but is wrong with initial values at the starting point of the recovery.We demonstrate the application of initial history by solving a forced fractional Lorenz system numerically.

KeywordsFractional derivative·Differential equation· Initial value·Initial history

1　Introduction

The fractional derivative has a history of more than 300 years［1-4］.A simple application of the fractional derivative is Scott Blair’s model［5］of viscoelastic materials, where the stress is proportional to the α-th order derivative of the strain.The model is a generalization［6］of Hooke’s law（α=0）for elastic materials,Newton’s law（α=1）for viscous materials,and Newton’s second law of motion （α=2）.Other applications in physics,for example,are found in models of materials［7-13］,the anomalous diffusion of particles［14-18］,the chaotic dynamics of fractional Lorenz system［19］,nondiffusive transport in plasma turbulence［20］,and quantum physics［21］.Books about the applications of the fractional derivative in physics are published in e.g.Refs.［22-24］.The fractional derivative has also been used in chemistry［25］,biology［26-28］,and psychology［29］,etc.Nevertheless,somefundamentalproblems have prevented the popularization of fractional calculus.For fractional differential equations with the Riemann-Liouville derivative,for example,the physical meanings of the initial values are unknown［1,30］.The Caputo derivative［31］（or Gerasimov-Caputo derivative［32］）was introduced to avoid thisdifficult.TheinitialvaluesintheCaputocasearesimilar to that of integer-order differential equations,so the physical meanings are known.However,it“can be applied only to special conditions”in polynomial form［33］.For a fractional differential equation,it has been well-accepted that the initial conditions are define at a point［1,2］.However,some works indicate that initial histories rather than initial values at a point have to be considered［30,33-39］.A work worthy of mention is the initialized operator［34-36］,in which a term of history is imposed into a conventional fractional derivative at the initial point.The initialized operator givesclear physical meanings of the initial conditions.Nonetheless,the initialized operator follows the conventional form because the imposed term maps/transforms the history into a point.An alternative study taking into account the history is to construct a partial differential equation［30,38］, where the initial state is a vector of infinit dimensions.As pointedout,“practicalinitializationbasedonstateestimation by observers has to be investigated”［30］.Other works are the straightforward versions［33,39］of initial history for the Riemann-Liouville derivative.Despite these recent works, most researchers still follow the conventional initialization theory of fractional differential equations.The established theory of point initializations seems sound,but we fin it is wrong.

2　History-dependent initializations for equations with the Riemann–Liouville derivative

The α-th order Riemann-Liouville derivative is define as where t=a is the starting point,m is the integer that satisfie m−1≤α＜m,and Γ is the Euler Gamma function defineby Γ（x）=∫0+∞tx−1e−tdt for x＞0.It holds that Γ（x+1）=xΓ（x）.The Riemann-Liouville derivative is a generalization of an integer order derivative and integral.For etxample,aDαty（t）=dy（t）/dt if α=1,andaDtαy（t）=∫ay（t）dt,if α=−1.

A typical conventional initial value problem of fractional differential equation［4］is define as

What the physical meanings are of the initial values bkhas been an open problem.The equivalent integral equation［4］of the conventional initial value problem Eq.（2）takes the form

It is conventionally assumed that the initial value bmin Eq. （2）is arbitrarily given,but we fin that the value can only be zero.In fact,for any continuous solution define in a closed right-neighborhood of the initial instant,there is a positive constant C such that y（t）≤C,then

It follows that

As pointed out in Ref.［40］and demonstrated with Example 1 below,the correct way is to defin an initial condition over an interval［39］,and we refer to the initial condition as initial history.A typical initial history problem is

The equivalent integral equation of Eq.（6）takes the form ［39］

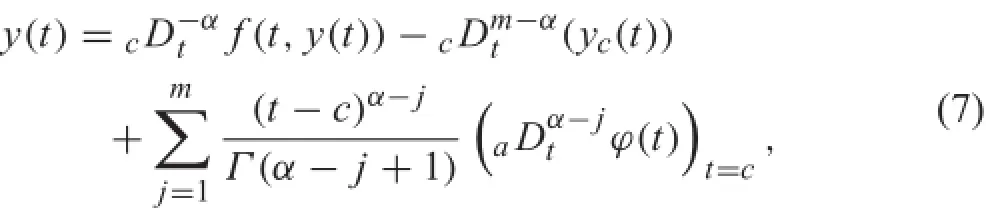
where for t＞c,

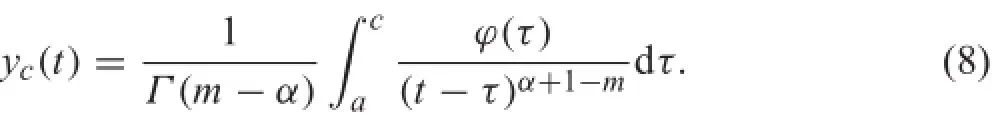
Note that yc（t）is improperly denoted byaDc−（m−α）y（t）in Ref.［39］.The initial condition of Eq.（6）has clear physical meaning.

Especially,if y（t）=0 for t≤c,Eqs.（6）and（7）,respectively,become

and

Intheworksaboutinitializedoperator,thehistoryconcept was already proposed.However,the terminal initialization “is analogous to choosing an arbitrary constant value to ini-tialize the integration of dy/dt in the solution of an ODE.”［36］Here,ODE stands for ordinary differential equation.

3　History-dependent initializations for equations with Caputo derivative

The Caputo derivative is define by

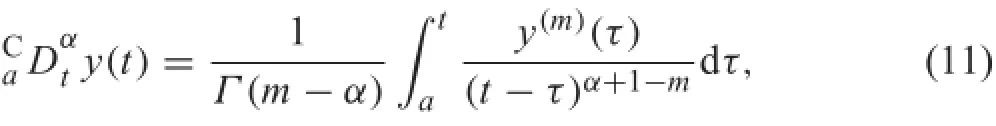
where m is the integer satisfie m−1≤α＜m.A typical conventionalinitialvalueproblem［4］withCaputoderivative is in the form of

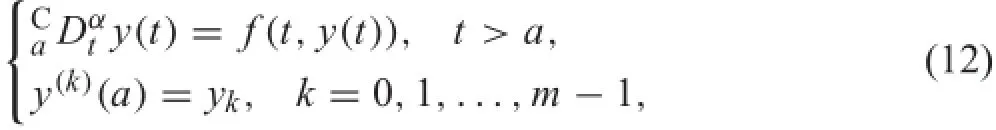
and the equivalent integral equation［4］of Eq.（12）is

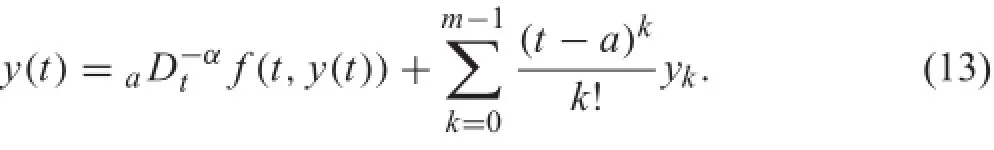
Equation（13）is a Volterra integral equation of the second kind.In view of history dependency,we defin an initial history problem

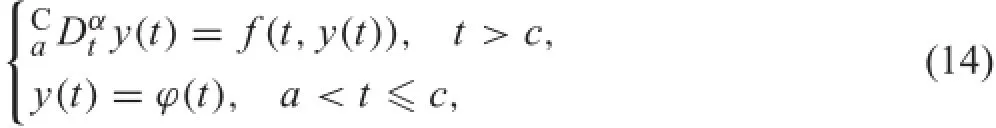
where y（t）hascontinuous（m−1）-thderivativeatt=c.The equivalent integral equation is

where,for t＞c,

Letcapproacha,andthephysicalmeaningofthesecondterm ontheright-handsideofEq.（15）isnotknown.Actually,this term is unnoticed in Eq.（13）.

To prove Eq.（15）,from Eq.（14）,we have

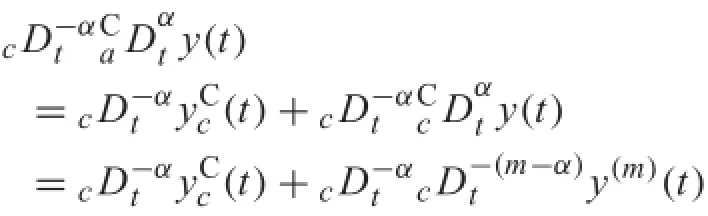
Inversely,

On both sides of Eq.（18）,adding,then applying,and assuming that y（t）=ϕ（t）for a＜t≤c,we obtain Eq.（14）.

To validate Eq.（15）,we consider a function

For t＞1,we have

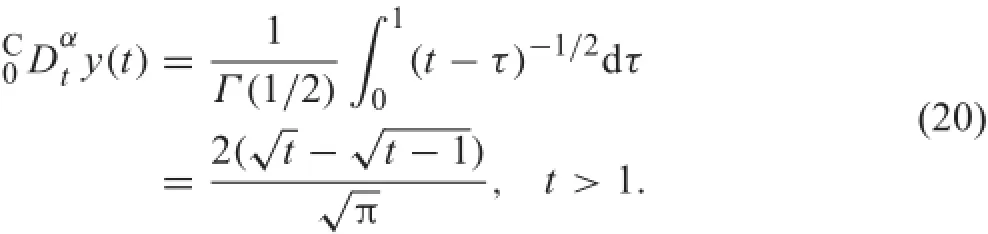
Equations（19）and（20）show that for t＞1,y（t）=1 is the solution of

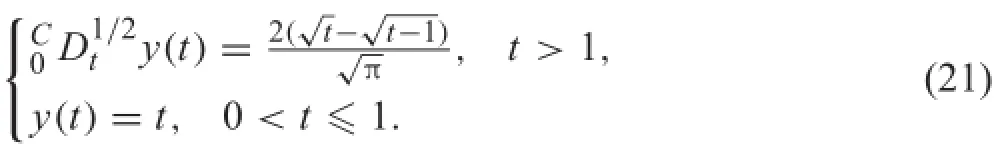
Actually,noting c=1 and ϕ（t）=t and using Eq.（15）, for t＞1

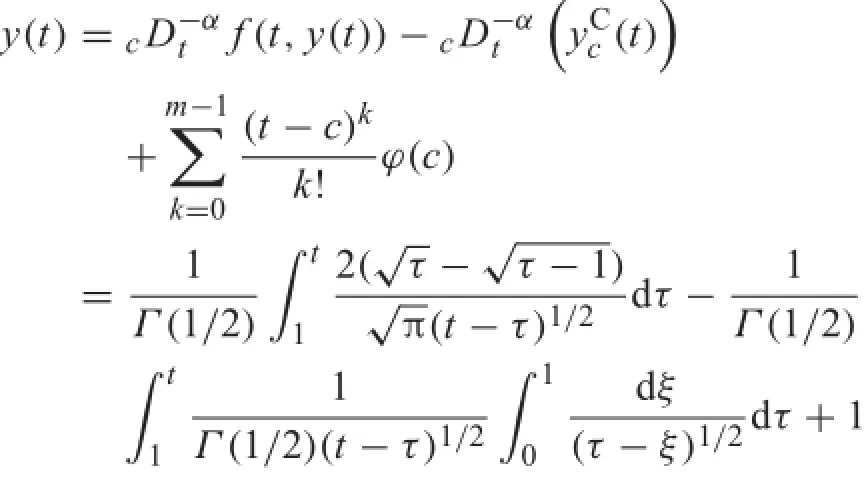
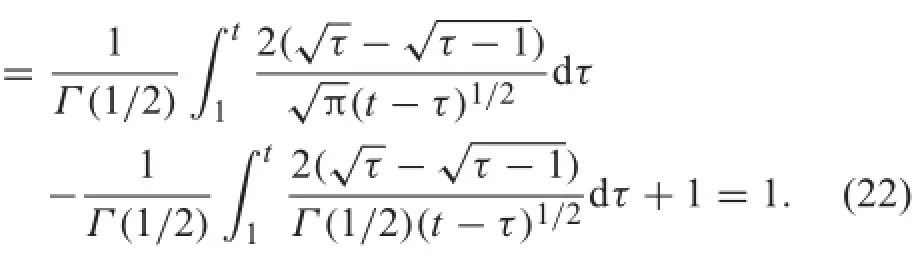
4　Examples

4.1Example 1

Asimplefractionaldifferentialequation,ScottBlare’smodel ［5］,can be used to model memory phenomena such as the creep and recovery of nitrocellulose compound［5］and SiA-lYON ceramics［39］,Ebbinghause’s learning and forgetting tests,and protein adsorption kinetics［29］.The model is

where μ is a physical constant.In viscoelastic material modeling,ε（t）is the strain,and σ（t）the stress.A standard test is usually performed with constant σ（t）=σ0in creep （0＜t≤tM）then σ（t）=0 in recovery（t＞tM）.With zero history ε（t）=0 for t≤0,using the equivalent integral Eq.（10）,the solutions of Eq.（23）are

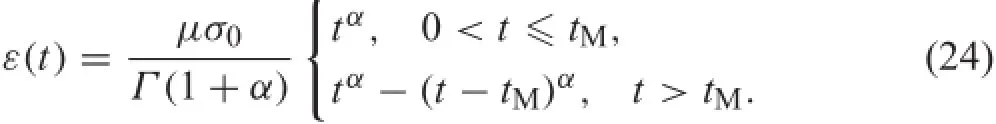
Some works describe history-dependent phenomena with power-law,forexample,inRefs.［41-45］.Althoughthesame solutionEq.（24）ofEq.（23）isobtainedwithzerohistoryand with conventional zero initial values,the physical meaning of the initial conditions are different.The former is clear, while the latter is not.Without loss of the physical property,let α=0.5,μ=1,σ0=1 for 0＜t≤1,and σ=0 for t＞1,Eq.（24）denotes the creep and recovery of a viscoelastic material as shown in Fig.1a.Replacing the Riemann-Liouville derivative with the Caputo derivative in Eq.（23）,the solution has the same form of Eq.（24）.

If the starting point is chosen to be t=1,for t＞1,we construct an initial history problem

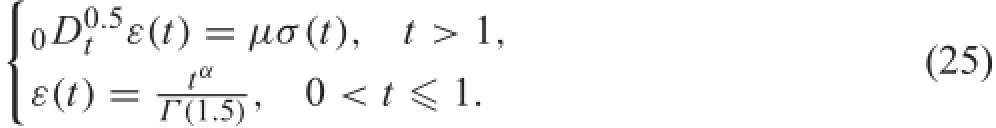
Using the equivalent integral Eq.（7）,the recovery behavior Eq.（24）still holds for t＞1.However,in a conventional way,if the starting point is t=1,in the recovery stage the deformation is governed by

Fig.1　Right and wrong initial conditions.a For the recovery stage, the red line represents the correct initial history.b The conventional initialization.The creep histories are removed and initializations are at point t=1.The dashed line represents the solution with the Caputo derivative,andthesolidlineisthesolutionwiththeRiemann-Liouville derivative

The solution of Eq.（26）is b（t−1）−0.5/Γ（0.5）.Since the physical meaning of the initial value b is unclear,we fi the initial value b=1 at will.As shown in Fig.1b the strain ε（t）goes to infinit as t approaches 1.Obviously this solution doesnotreflec therecoveryofanyviscoelasticmaterial.For the Caputo derivative,in the recovery stage,

The solution of Eq.（27）is a constant,namely ε（t）=ε（1）= 1/Γ（1.5）for t＞1.This constant solution,as shown in Fig.1b,also does not agree with the recovery behavior of real materials.

4.2Example 2

Inapplication,theanalysisbecomesmucheasierifaproblem can be constructed with zero history.For demonstration,we consider a forced fractional Lorenz system

where σ=10,r=28,b=3/8,Fx=σF,and Fy=−F throughoutthisexample.Equation（28）isageneralizationof the model of monsoon prediction,and it is a strange attractor when F=1［46］.If F=0 and α=0.99,Eq.（28）with dimension 2.97＜3,under conventional initial condition （10,0,10）,has a chaotic solution［19］.

We assume

With zero history x（t）=0,y（t）=0,z（t）=0 for t≤0, we determine the solutions of Eq.（28）numerically withα= 0.99 and step size 0.0005［47］.The solutions are shown in Figs.2,3,4.

Fig.2　The x components of the forced Lorenz system.a A=1.For t≤A and t＞A,the x（t）components are shown in red and black lines,respectively.b A=33.For A=1,2,...,33,the behaviors of the system are similar

Fig.3　Phase-space portrait of the forced Lorenz system for A=34 and t∈［0,100］

If x（t）,y（t）,and z（t）are measured in advance for t≤A, for example,x（t）shown in red lines in Fig.2,we can construct a history problem given these non-zero initial conditions.For t＞A,the solutions are the same as that of the modelbeginatt=0,butthecalculationismorecomplicated withEq.（7）.Figure2showsthatthesolutionsarenotchaotic when A=1,2,...,33.Theyaredifferentfromthecommon Lorenz system［48］,which is globally chaotic with σ=10, r=28,b=3/8.In this case the behaviors of fractional dynamical systems are more convenient to predict than that of the corresponding integer order systems.Increasing A to 34,chaos occurs as shown in Figs.3 and 4.

Fig.4　The x components of the forced Lorenz system.（a-c）Respectively,very closed initial conditions A=33.9995,34,and 34.0005 yield far apart solutions

5　Conclusions

Weshowthattheconventionalinitializationoffractionaldifferential equation is wrongly define at a point.We propose and validate history-dependent initializations.In this way, the dimension of a fractional differential equation is infinit because the initial conditions are define in function spaces. Since our finding are fundamental,many established theories and applications require modification

AcknowledgmentsThisworkwassupportedbytheNationalNatural Science Foundation of China（Grants 11372354 and 10825207）.

References

1.Podlubny,I.:Fractional Differential Equations.Academic Press, San Diego（1999）

2.Oldham,K.B.,Spanier,J.:The Fractional Calculus.Academic Press,New York（1974）

3.Miller,K.S.,Ross,B.:An Introductory to the Fractional Calculus and Fractional Differential Equations.John Wiley&Sons Inc., New York（1993）

4.Kilbas,A.A.,Srivastava,H.M.,Trujillo,J.J.:Theory and Applications of Fractional Differential Equations.Elsevier,Amsterdam （2006）

5.Stiassnie,M.:Ontheapplicationoffractionalcalculusforformulationofviscoelasticmodels.Appl.Math.Model.3,300-302（1979）

6.Velasco,M.P.,Vzquez,L.:On the fractional Newton and wave equation in one space dimension.Appl.Math.Model.38,3314-3324（2014）

7.Tan,W.C.,Xu,M.Y.:Unsteadyflwsofageneralizedsecondgrade fluiwith the fractional derivative model between two parallel plates.Acta Mech.Sin.20,471-476（2004）

8.Qi,H.T.,Jin,H.:Unsteady rotating flws of a viscoelastic flui withthefractionalMaxwellmodelbetweencoaxialcylinders.Acta Mech.Sin.22,301-305（2006）

9.Hayat,T.,Khan,M.,Asghar,S.:On the MHD flw of fractional generalized Burgers’flui with modifie Darcy’s law.Acta Mech. Sin.23,257-261（2007）

10.Hu,K.X.,Zhu,K.Q.:The exact solution of Stokes second problem includingstart-upprocesswithfractionalelement.ActaMech.Sin. 25,577-582（2009）

11.Jamil,M.,Fetecau,C.,Fetecau,C.:Unsteady flw of viscoelastic flui between two cylinders using fractional Maxwell model.Acta Mech.Sin.28,274-280（2012）

12.Rossikhin,Y.A.,Shitikova,M.V.:Applicationoffractionalcalculus for dynamic problems of solid mechanics:novel trends and recent results.Appl.Mech.Rev.63,101080（2010）

13.Papoulia,K.D.,Panoskaltsis,V.P.,Kurup,N.V.,et al.:Rheological representation of fractional order viscoelastic material models. Rheol.Acta 49,381-400（2010）

14.Metzler,R.,Jeon,J.-H.,Cherstvy,A.G.,etal.:Anomalousdiffusion models and their properties:non-stationarity,non-ergodicity,and ageing at the centenary of single particle tracking.Phys.Chem. Chem.Phys.16,24128-24164（2014）

15.Lutz,E.:Fractional langevin equation.Phys.Rev.E 64,051106 （2001）

16.Mandelbrot,B.B.,Ness,J.W.V.:Fractionalbrownianmotions,fractional noises and applications.SIAM Rev.10,422-437（1968）

17.Friedrich,R.,Baule,F.J.A.:Anomalous diffusion of inertial, weakly damped particles.Phys.Rev.Lett.96,230601（2006）

18.Bisquert,J.:Fractional diffusion in the multiple-trapping regime and revision of the equivalence with the continuous-time random walk.Phys.Rev.Lett.91,010602（2003）

19.Grigorenko,I.,Grigorenko,E.:Chaotic dynamics of the fractional Lorenz system.Phys.Rev.Lett.91,034101（2003）

20.delCastillo-Negrete,D.,Carreras,B.A.,Lynch,V.E.:Nondiffusive transport in plasma turbulence:a fractional diffusion approach. Phys.Rev.Lett.94,065003（2005）

21.Laskin,N.:Fractionalquantummechanics.Phys.Rev.E 62,3135-3145（2000）

22.Uchainkin,V.V.:Fractional Derivative for Physicists and Engineers,vol.II.Applications.High Education Press,Beijing（2013）

23.Herrmann,R.:FractionalCalculus:AnIntroductionforPhysicists. World Scientific Hackensack（2011）

24.Hilfer,R.:Applications of Fractional Calculus in Physics.World Scientific Singapore（2000）

25.Toledo-Hernandez,R.,Rico-Ramirez,V.,Iglesias-Silva,G.A., et al.:A fractional calculus approach to the dynamic optimization of biological reactive systems.Part I:Fractional models for biological reactions.Chem.Eng.Sci.117,217C228（2014）

26.Magin,R.L.:Fractional calculus in bioengineering.Crit.Rev.Biomed.Eng.32,1-104（2004）

27.Davis,G.B.,Kohandel,M.,Sivaloganathan,S.,et al.:The constitutive properties of the brain paraenchyma:Part 2.Fractional derivative approach.Med.Eng.Phys.28,455-459（2006）

28.Lundstrom,B.N.,Higgs,M.H.,Spain,W.J.,et al.:Fractional differentiation by neocortical pyramidal neurons.Nat.Neurosci.11, 1335-1342（2008）

29.Du,M.L.,Wang,Z.H.,Hu,H.Y.:Measuring memory with the order of fractional derivative.Sci.Rep.3431（2013）

30.Trigeassou,J.C.,Maamri,N.,Sabatier,J.,etal.:Statevariablesand transients of fractional order differential systems.Comput.Math. Appl.64,3117-3140（2012）

31.Caputo,M.:Linear models of dissipation whose Q is almost frequency independent-II.Geophys.J.R.Astron.Soc.13,529-539 （1967）.Reprinted.In:Fractional Calculus&Applied Analysis 11, 4-14（2008）

32.Uchainkin,V.V.:Fractional Derivative for Physicists and Engineers,vol.I.Background and Theory.High Education Press, Beijing（2013）

33.Fukunaga,M.,Shimizu,N.:Role of prehistories in the initial value problems of fractional viscoelastic equations.Nonlinear Dyn.38, 207-220（2004）

34.Lorenzo,C.F.,Hartley,T.T.:Initialization,conceptualization,and applicationinthegeneralizedfractionalcalculus.NASATP1998-208415.National Aeronautics and Space Administration,Lewis Research Center（1998）

35.Lorenzo,C.F.,Hartley,T.T.:Initialized fractional calculus,NASA TP2000-209943.NationalAeronauticsandSpaceAdministration, Glenn Research Center（2000）

36.Lorenzo,C.F.,Hartley,T.T.:Initialization of fractional-order operators and fractional differential equations.J.Comput.Nonlinear Dyn.3,021101（2008）

37.Hartley,T.T.,Lorenzo,C.F.,Trigeassou,J.-C.,et al.:Equivalence of history-function based and infinite-dimensional-stat initializations for fractional-order operators.J.Comput.Nonlinear Dyn.8, 041014（2013）

38.Trigeassou,J.C.,Maamri,N.:Initial conditions and initialization of linear fractional differential equations.Signal Process.91,427-436（2011）

39.Du,M.L.,Wang,Z.H.:Initialized fractional differential equations with Riemann-Liouville fractional-order derivative.Eur.Phys.J. Spec.Top.193,49-60（2011）

40.Bandyopadhyay,B.,Kamal,S.:Stabilization and Control of Fractional Order Systems:A Sliding Mode Approach.Springer, Heidelberg（2015）

41.Nutting,P.G.:A new general law of deformation.J.Frankl.Inst. 191,679-685（1921）

42.Chaplain,R.A.:Simple viscoelastic model for the stress relaxation of rubber vulcanizates.Nature 220,1028-1029（1968）

43.Cherstvy,A.G.,Metzler,R.:Population splitting,trapping,and non-ergodicity in heterogeneous diffusion processes.Phys.Chem. Chem.Phys.15,20220-20235（2013）

44.Cherstvy,A.G.,Chechkin,A.V.,Metzler,R.:Ageing and confine ment in non-ergodic heterogeneous diffusion processes.J.Phys.A 47,485002（2014）

45.Cherstvy,A.G.,Chechkin,A.V.,Metzler,R.:Particle invasion, survival,and non-ergodicity in 2D diffusion processes with spacedependent diffusivity.Soft Matter 10,1591-1601（2014）

46.Mittal,A.K.,Dwivedi,S.,Pandey,A.C.:Bifurcation analysis of a paradigmatic model of monsoon prediction.Nonlinear Process. Geophys.12,707-715（2005）

47.Diethelm,K.,Ford,N.J.,Freed,A.D.:A predictor-corrector approach for the numerical solution of fractional differential equations.Nonlinear Dyn.29,3-22（2002）

48.Lorenz,E.N.:Deterministic nonperiodic flw.J.Atmos.Sci.20, 130-141（1963）

15 February 2015/Revised:2 May 2015/Accepted:6 May 2015/Published online:14 August 2015

✉Zaihua Wang

zhwang@nuaa.edu.cn

1Institute of National Defense Engineering,PLA University of

Science and Technology,Nanjing 210007,China

2Institute of Science,PLA University of Science and

Technology,Nanjing 211101,China

3State Key Laboratory of Mechanics and Control of

Mechanical Structures,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China