基于随机真度的理论的随机相容度分布
2016-09-05李修清魏海新
李修清 魏海新
(1 桂林航天工业学院 理学部,广西 桂林 541004;2 桂林航天工业学院 计算机科学与工程系,广西 桂林 541004)
基于随机真度的理论的随机相容度分布
李修清*1魏海新2
(1桂林航天工业学院理学部,广西桂林541004;2桂林航天工业学院计算机科学与工程系,广西桂林541004)

随机真度;随机直径;随机相容度
以王国俊为代表的一批数学家,对以符号化为特点的数理逻辑进行了数值运算研究,从而产生了计量逻辑学[1-4]。计量逻辑学中考虑的命题公式真度,是以概率的均匀分布为基础的,惠小静,李修清等在计量逻辑学的基础上,进一步考虑一般概率的情形,提出了随机真度的概念,将计量逻辑学的结论推广到了随机化的情形[5-11]。

1 随机逻辑度量空间
首先给出要用到的概念和性质,没有说明的符号和概念,可参见文献[12]。
设S={q1,q2,…}是命题变元(或原子命题)集,F(S)是由S生成的(,∨,→)型自由代数,称F(S)中的元素为命题公式或公式。

设N={1,2,…}为自然数的集合, 设p=(p1,p2,…),其中p1=(p11,p21)T,p2=(p12,p22)T,…,均为任意的两点概率分布,且pij>0(i=1,2;j=1,2,…),则我们称p=(p1,p2,…)为随机两点分布序列。其中概率分布p1,p2,…是相互独立的。我们记Ρ为随机两点分布序列的集合,即
Ρ={p=(p1,p2,…)|p为随机两点分布序列}。
设p=(p1,p2,…)是随机两点分布序列,且p1=(p11,p21)T,p2=(p12,p22)T,…,∀α=(x1,…,xm)∈{0,1}m,令φp(α)=φp1(x1)×φp2(x2)×…×φpm(xm),定义为:当xi=0时φpi(xi)=p1i,当xi=1时φpi(xi)=p2i(i=1,…,m),则显然得到一个m维映射φp:{0,1}m→(0,1),我们称为空间{0,1}m的一个p-随机化映射,简称随机化映射。


定义1.1设A=A(q1,…,qm)∈F(S)是含有m个命题变元的命题公式,p=(p1,p2,…)为任取的随机两点分布序列,φp为{0,1}m上的p-随机化映射,令
则称τp(A)为命题公式A的p-随机真度,或随机真度。
由随机真度的定义易得
命题1.1设A=A(q1,…,qm)∈F(S)是含有m个命题变元的命题公式,p=(p1,p2,…)为任取的随机两点分布序列,则
下面给出随机真度的一些基本性质。
定理1.1设A,B∈F(S),则:
(ⅰ)若A是重言式,则∀p∈Ρ均有τp(A)=1;反之,若∃p∈Ρ使τp(A)=1,则A是重言式。
(ⅱ)若A是矛盾式,则∀p∈Ρ均有τp(A)=0;反之,若∃p∈Ρ使τp(A)=0,则A是矛盾式。

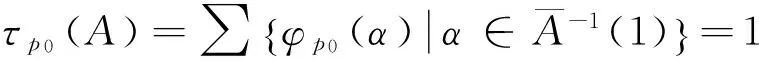
(ⅱ)同理可证。证毕。
定理1.2[5]设A,B∈F(S),∀p∈Ρ,则以下各结论成立:
(ⅰ)τp(A)=1-τp(A)。
(ⅱ)τp(A∨B)=τp(A)+τp(B)-τp(A∧B)。
由随机真度的性质,我们可以引入随机伪距离的概念,从而建立随机逻辑度量空间。
定义1.2[6]设A,B∈F(S),∀p∈Ρ,令
δp(A,B)=τp((A→B)∧(B→A))
则称δp(A,B)为公式A与B之间的p-随机相似度或随机相似度。显然δp(A,B)=δp(B,A)。又定义ρp(A,B)=1-δp(A,B),称ρp(A,B)为公式A与B之间的p-随机伪距离或随机伪距离,这时空间(F(S),ρp)称为p-随机逻辑度量空间或随机逻辑度量空间[6]。
要证明ρp(A,B)是随机伪距离,还要用到下面关于随机相似度的结论,具体论述参见文献[5-6]。
定理1.3[6]设A,B,C∈F(S),∀p∈Ρ,则
(ⅰ)A≈B当且仅当δp(A,B)=1;
(ⅱ)δp(A,B)+δp(B,C)≤1+δp(A,C)。
2 理论的随机相容度的分布
定义2.1[12]设Γ∈F(S),则Γ称为一个理论,若存在一个有限的公式序列A1,A2,…,An,对于每一个Ai(i≤n),Ai是公理或Ai∈Γ,或存在j,k≤i,使Ai是由Aj与Ak使用MP规则推出的结果,则称An为Γ-结论,记作ΓAn。当Γ是空集时,称Γ的结论A为定理,记作A。Γ的全体结论之集,记作D(Γ)。若D(Γ)=Γ,则称Γ为逻辑闭理论。


为了研究理论的随机相容度问题,先给出理论的随机直径、随机极指标等概念。
定义2.2设Γ是F(S)的一个理论,D(Γ)是理论Γ的全体结论之集,∀p∈Ρ,

称dp(Γ)为理论Γ的p-随机直径或随机直径。
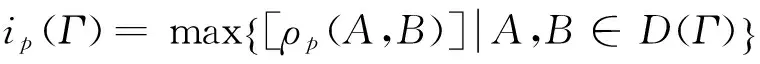

定理2.1[8]∀p∈Ρ,设Γ是F(S)的一个理论,则Γ是相容理论当且仅当ip(Γ)=0,Γ是不相容理论当且仅当ip(Γ)=1。
定义2.3[8]设Γ是F(S)的一个理论,∀p∈Ρ,
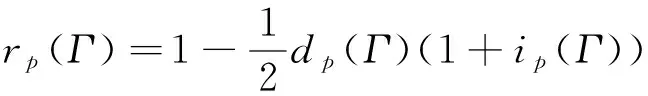
称rp(Γ)为理论Γ的p-随机相容度或随机相容度。
定理2.2设Γ是F(S)的一个理论,p是任取的两点分布序列,则
(ⅰ)Γ是不相容理论当且仅当rp(Γ)=0;


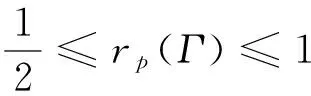
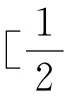
为了证明的需要,首先给出伪距离的一个结论。
定理2.3设A,B∈F(S),∀p∈Ρ,则ρp(A,B)=τp(A∨B)-τp(A∧B)。
证明:在二值命题逻辑系统中,就a,b∈{0,1}的不同情形,容易验证下面的等式成立:
1-(a→b)∧(b→a)=(a∨b)-(a∧b)


上式两边同乘随机化映射φp(α)得:


上面等式两边对α∈{0,1}m求和得:
故由命题1.1得:
1-δp(A,B)=τp(A∨B)-τp(A∧B),即得:ρp(A,B)=τp(A∨B)-τp(A∧B)。证毕。
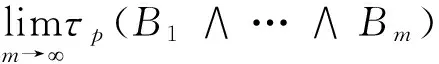

我们知道,在计量逻辑学中全体命题变元之集S的直径为1[4],但对于随机真度而言,全体命题变元之集S的p-随机直径要复杂的多,为了研究其随机直径,先给出下面定理。

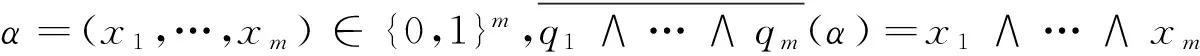

∀α∈(0,1),则由对数的意义,显然有-lnα∈(0,+),记为β,即设β=-lnα,我们构造两点分布序列p=(p1,p2,…)如下:令。则对于我们构造的这个两点分布序列有,
由级数的计算公式易得:

定理2.5设S是全体命题变元的集合,则对于任何一个实数0<α≤1,都存在两点分布序列p=(p1,p2,…),使dp(S)=α。
证明对于α=1,取均匀两点分布序列p0=(p10,p20,…),则有dp0(S)=1(见文献[4])。设α∈(0,1),则显然1-α∈(0,1),则由定理2.4知,存在两点分布序列p=(p1,p2,…),使

这个定理说明,全体命题变元集S的随机直径是与随机两点分布序列p的取值相关的,且得出了S的随机直径可以随着p的不同取值,等于区间(0,1]中的任何一个实数。



3 结束语
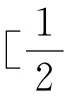
[1]Wang G J, Leung Y. Integrated semantics and logic metric spaces[J]. Fuzzy Sets and Systems,2003,136(1):71-91.
[2]王国俊,李壁镜.Lukasiewiczn值命题逻辑中公式的真度理论和极限定理[J].中国科学:E辑,2005,35(6):561-569.
[3]王国俊,王伟.逻辑度量空间[J].数学学报,2001,44(1):159-168.
[4]王国俊.计量逻辑学(Ⅰ) [J].工程数学学报,2006,23(2):191-215.
[5]惠小静,王国俊.经典推理模式的随机化研究及其应用[J].中国科学:E辑,2007,37(6):801-812.
[6]惠小静,王国俊.经典推理模式的随机化研究及其应用(Ⅱ)[J].模糊系统与数学,2008,22(3):21-26.
[7]惠小静.三值R0命题逻辑系统的随机化[J].应用数学学报,2009,32(1):19-27.
[8]惠小静,李宏设,李丽.D-逻辑度量空间中的相容理论[J].模糊系统与数学,2009,23(2):12-17.
[9]李修清,魏海新,林亮.修正的n值Gödel逻辑系统的随机化[J].计算机工程与应用,2012,48(24):45-49.
[10]李修清,朱宁.R0型命题逻辑系统的随机化[J].模糊系统与数学,2013,27(1):63-70.
[11]李修清,魏海新.n值Lukasiewicz逻辑系统中理论的随机发散度[J].模糊系统与数学,2013,27(6):93-98.
[12]王国俊.数理逻辑引论与归结原理(第二版)[M].北京:科学出版社,2006.
(责任编辑骆桂峰)
O141.1
A
2095-4859(2016)02-0221-05
**作者简介:李修清,男,河南清丰人。教授。研究方向:布尔代数、数理逻辑。
