双动压力机用压边滑块串联四连杆工作机构的优化

贾　先　赵升吨　范淑琴　谭栓斌

1.西安思源学院，西安，710038　　2.西安交通大学，西安，710049



双动压力机用压边滑块串联四连杆工作机构的优化

贾先1赵升吨2范淑琴2谭栓斌1

1.西安思源学院，西安，7100382.西安交通大学，西安，710049

针对J45-315型闭式单点双动拉延压力机所使用的杆系长度与角度尺寸不合理的机构所造成的外滑块压边过程中位移波动量大，严重影响板材拉延过程中压边效果的问题，建立了该机构的优化数学模型，运用步长搜索法对外滑块的位移波动量进行了优化。优化后的研究结果表明，外滑块位移波动量由原来的0.092mm减小到0.015mm，即压边外滑块位移波动量比原机构减小83.7%时，外滑块压紧角增大3.4%，有效提高了双动拉延机械压力机冲压的工作性能，从而为双动拉延机械压力机压边用外滑块驱动的工作机构优化打下了基础。

双动拉延机械压力机；串联四连杆工作机构；运动特性

0　引言

我国汽车产销总量多年位居全球第一。汽车工业的迅速发展，迫切需要大吨位压力机和深拉延性能好的优质冷轧钢板来满足车身生产需求，这就促进了深拉延冷轧薄钢板的大量生产。

薄板深拉延工艺可在单动、双动和三动等压力机上进行[1-2]。对于形状比较复杂的拉深件，为了防止零件周边起皱需要采用压边装置，一般都在双动拉延压力机上进行拉深[1]。在双动压力机压边开始时，外滑块已处于极限位置(连杆机构处于共线位置)，滑块运行速度接近于零，接触冲击很小，因而双动拉延压力机主要用于拉延形状较为复杂的零件。这种压力机有两个滑块，即内滑块和外滑块。外滑块用于压边，内滑块用于拉深毛坯[3]。在压紧角内，最理想的状态是外滑块不动，但该机构的外滑块不可避免地有微小的波动。拉延工艺要求外滑块的波动量不超过0.050 mm。对于外滑块传动机构这样复杂而要求较高的机构，传统设计只能用作图的方法，靠相关经验或直观判断来试凑外滑块的波动量，外滑块的波动量往往达不到拉延工艺的要求，需要继续优化。如J45-315型闭式单点双动压力机的外滑块波动量为0.092 mm，严重影响压边效果和拉延件的质量。

传统的连杆机构设计方法计算量大，精度不高[4-12]。本文以J45-315型闭式单点双动拉延机械压力机为例，以其外滑块在压紧角范围内的位移波动量为研究对象，以外滑块的波动量在满足限定数值的前提下，压紧角最大为目标函数，建立了外滑块机构的优化模型，在MATLAB软件中运用步长搜索法改变各个设计变量，从而得出J45-315型闭式单点双动压力机外滑块传动机构的构件尺寸参数的最优解。

1　外滑块驱动机构的三种类型及其特点分析

在双动拉延压力机上拉延零件时，零件毛坯周边的压边力是由外滑块(又称压边滑块)产生的。外滑块由多连杆机构或凸轮机构驱动，作近似停歇运动。当内滑块(又称拉延滑块)进行拉延时，外滑块压紧毛坯周边。驱动外滑块的连杆机构一般采用串接四连杆机构，它是由三组四连杆机构串联而成的，利用其在曲柄与连杆共线位置附近，主动曲柄与从动摇杆间较大的瞬时减速比，当被串接的四连杆机构数增加，并且均在共线位置附近工作时，机构可获得很大的降速比。

串联四连杆机构可分为三类：单边驱动串联四连杆机构、双边驱动的串联四连杆机构和三角摆杆式串联四连杆机构。

单边驱动串联四连杆机构(图1)由曲柄摇杆机构OABO1、双摇杆机构O1CDO2和曲柄滑块机构O2EF共同组成。滑块和机架之间存在4个移动副，其中3个移动副为虚约束，虚约束可以使外滑块受力均衡，刚度增大，但同时要求4个移动副的导路务必要平行，如果由于制造和安装的误差使4个移动副的导路不平行，虚约束就会转化为有效约束，使整个机构不能运动。

图1　单边驱动串联四连杆机构

双边驱动的串联四连杆机构(图2)是由3个曲柄滑块机构OAB、O1DE和O1EF共同组成，该机构的特点是左右两边各由完全对称的2个曲柄滑块机构组成，这样可以使外滑块受力均衡，刚度增大，但同时要求左右两边的机构完全对称。如果由于制造和安装的误差使左右两边的机构不完全对称，整个机构将不能运动。

图2　双边驱动的串联四连杆机构

三角摆杆式串联四连杆机构(图3)不存在虚约束，只要设计变量合理，就能实现预期的运动规律。对制造和安装精度要求不高，可以降低成本，提高机构运动的可靠性。所以双动拉延机械压力机压边滑块采用三角摆杆式串联四连杆机构时综合性能较好。

图3　三角摆杆式串联四连杆机构(J45-315型)

事实上在内滑块拉延外滑块压边过程中，外滑块并非绝对静止不动，而是在夹紧角范围内做近似的停顿，即有微量波动Δs，Δs愈小压边效果愈好，外滑块(以下简称滑块)压边力即为压力机受力零件(机身等)的弹性恢复力，它由调节装模高度的方法控制。在压边过程中，滑块停顿时的波动量Δs和滑块压紧角(滑块压边过程中主动曲柄转过的角度)ψ的值必须符合技术条件的规定，在夹紧角范围内外滑块的位移波动量Δs应远小于压力机受力零件的弹性变形量，微量波动Δs值在设计时由技术要求规定，根据参考文献[13],一般取0.030～0.050mm，波动越小压边效果越好。双动拉延压力机外滑块要求压力机在内滑块工作行程开始前10°～15°压紧坯料，超前量取内滑块行程的0.1～0.15倍。“超前”能保证外滑块在拉延前压紧毛坯。为了使拉延零件不致卡在上模上，外滑块应滞后于内滑块10°～15°回程。在内滑块到达上死点时，外滑块已经过自己的上死点开始向下行。向下行程量应保证拉延零件能从模具中取出。行程长度与内滑块行程长度之比一般取0.6～0.7。外滑块的压紧角ψ一般取100°左右。为扩大压力机的应用范围(能拉延更深的拉延件)，应尽量使外滑块的压紧角为最大[14]。

2　串联四连杆机构滑块运动特性的理论分析

J45-315型闭式单点双动压力机外滑块三角摆杆式串联四连杆机构如图3所示，其主要工作参数见表1。该机构是由3个四杆机构串联而成的八连杆间歇运动机构，即由曲柄摇杆机构OABC、双摇杆机构CDEO和曲柄滑块机构OFG共同组成。整个外滑块机构首先由曲柄摇杆机构OABC中的曲柄OA通过连杆AB带动摇杆BC做往复摆动，三角连杆BCD中杆BC和杆CD做同步往复摆动，由杆CD将运动传入双摇杆机构CDEO，通过杆DE带动杆EO做往复摆动，角杠杆OEF中杆EO和杆OF做同步往复摆动，将运动传入曲柄滑块机构OFG，由杆OF的往复摆动带动滑块G上下运动。

表1　J45-315型双动拉延机械压力机技术参数表

由于四杆机构在曲柄与连杆共线位置附近，曲柄与摇杆之间有较大的减速比，所以可通过合理确定机构设计参数，使3个四杆机构各自的减速运动衔接起来，从而在主动曲柄OA的某一规定转角范围内，实现滑块G在其下死点的近似停顿，即实现压边。

假设曲柄以顺时针方向等角速度ω旋转，该机构共有12个变量：曲柄OA长度R,连杆AB长度L2，三角连杆BCD中杆BC长度L3，三角连杆BCD中CD杆长度L4，连杆DE长度L5，三角连杆EOF中杆OE长度L6，三角连杆EDF中杆OF长度L7，连杆FG长度L8，机架上OC两点之间的水平距离X,机架上OC两点之间的垂直距离Y,角杠杆EOF中杆OE和OF夹角δ1，角杠杆BCD中杆BC和CD夹角δ2。由解析法得出三角摆杆式串联四连杆机构的运动学方程如下：

(1)滑块位移方程为

s=L7+L8-L7cosφ5-L8cosβ

(1)

为了简化运动学方程，特引入中间变量H、I、M、N、a、b、c、d：

a=Y+Rcosα

b=X+Rsinα

则

(2)

(2)滑块速度方程为

(3)

(3)滑块加速度方程为

(4)

3　串联四杆机构优化模型的建立

如何正确选择各杆长度和有关参数，以保证Δs和ψ满足工艺要求是该机构设计的关键。以往用图解法设计，不能保证机构具有最佳运动特性，而且设计工作量很大。如果用解析法求设计参数，则问题归结为求解由机构待定参数组成的非线性方程组，待定参数多，求解困难。然而用最优化设计方法，则可克服上述困难，求得最佳设计参数，在满足给定的Δs条件下使压紧角ψ值最大，从而获得具有最佳运动特性的机构，大大提高设计效率，缩短设计时间。

本次优化的目的为使外滑块波动量Δs满足限定值时，压紧角ψ最大。

3.1设计变量

如图3所示，三角摆杆式串联四连杆机构共有个12个设计变量。设计变量向量为

X=(x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12)T=

(R,L2,L3,L4,L5,L6,L7,L8,X,Y,δ1,δ2)T

(5)

3.2约束条件

满足某些限制条件的设计才是可行的设计，这些限制条件就是约束条件。三角摆杆式串联四连杆机构的约束条件如下：

(6)

(7)

g7(X)=L8-L7≥0

(8)

式(6)为曲柄摇杆机构OABC存在的条件，式(7)为双摇杆机构CDEO存在的条件，式(8)为滑块机构OFG存在的条件。

外滑块最大位移smax应满足压力机技术参数所规定的外滑块行程量的要求：

(9)

(10)

式中，sH1为外滑块位移最大值smax允许变化的下限；sH2为外滑块位移最大值smax允许变化的上限；sH为压力机技术参数规定的外滑块行程量；Δsm为位移最大值smax允许变化的量。

以Rmax和Rmin分别表示所允许的R的最大值和最小值，其余各变量依次与此类同表示,则12个设计变量的边界条件总共有24个：

(11)

3.3目标函数

根据双动拉延压力机外滑块压边的工艺要求，在其下死点做微量波动时，在满足给定的Δs条件下使ψ值最大，这个角度即为外滑块的压紧角。因外滑块开始停歇时曲柄的位置α0和压紧角ψ未知，Δα和Δψ分别为运用步长搜索法时曲柄的位置α和压紧角ψ的步长增量，ψ0为满足给定的Δs条件下的压紧角ψ的最大值。目标函数可通过图4所示的流程计算得到。

图4　目标函数计算流程简图

设目标函数为

minf(x)=-ψ

(12)

式(5)～式(12)为双动压力机滑块串联四杆机构的优化模型。这是一个具有12个独立自变量和33个不等式约束的非线性规划问题。

4　最优化计算及其结果

将原来设计的J45-315型双动压力机外滑块机构的各个设计变量输入到MATLAB软件中,对其机构数学模型编写运动特性仿真程序，设滑块行程次数为9次/min，对其运动学特性进行模拟仿真，可得原机构在压紧角ψ内(Δs=0.092mm)的滑块位移、速度、加速度曲线，如图5所示。

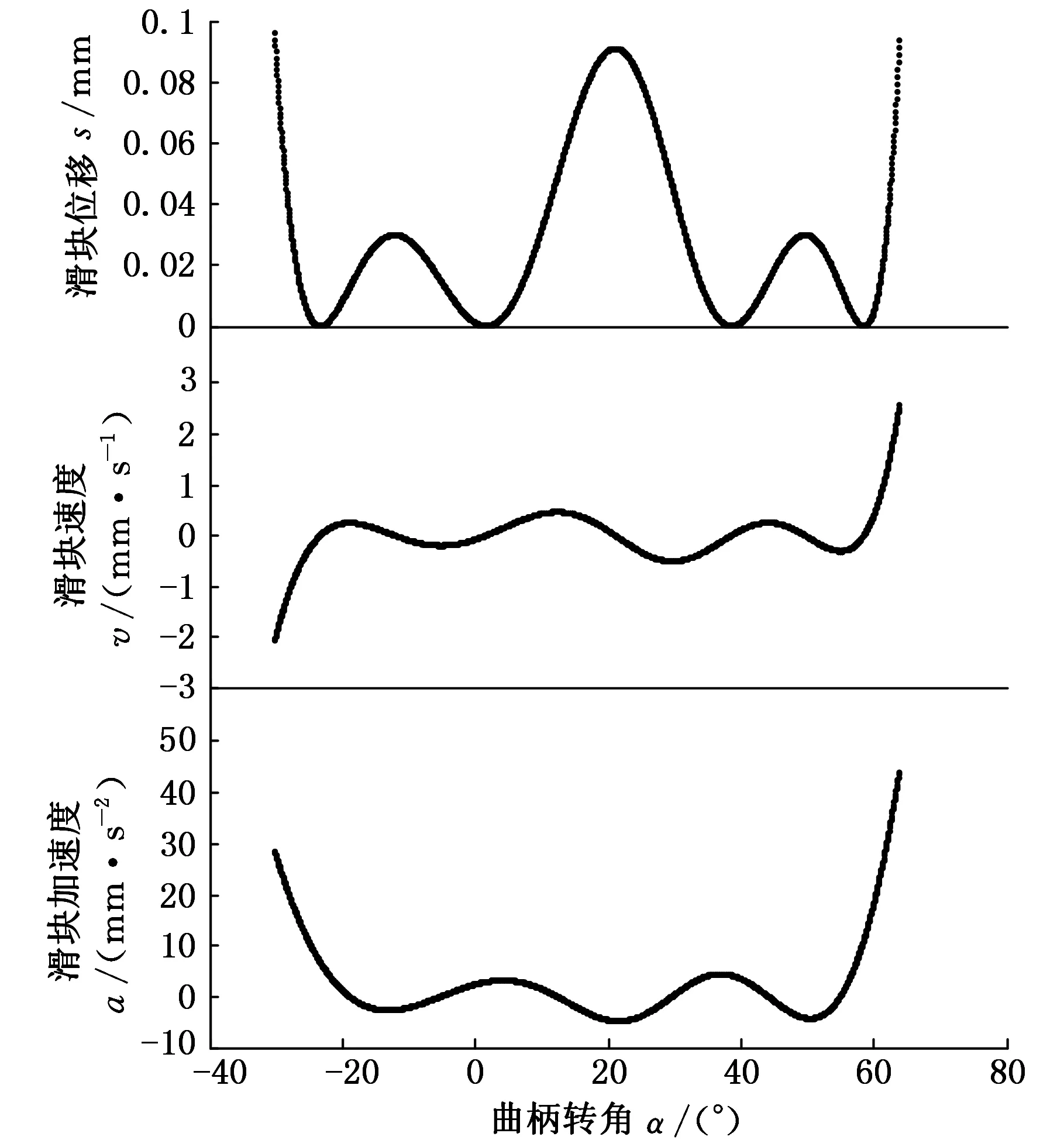
图5　原机构在压紧角内运动曲线

从图5可以看出原机构中，滑块微波动量Δs=0.092mm，压紧角ψ=93.908°，在压紧角ψ内滑块最大速度vmax=2.525mm/s,最大加速度amax=43.966mm/s2。

限定串联四杆机构滑块微波动量为Δs=0.015mm，在MATLAB软件中运用步长搜索法改变各个设计变量值进行优化，优化后机构各部分的尺寸和对应的外滑块压紧角ψ如表2所示。

表2　优化前后有关数据

设滑块行程次数9次/min，利用MATLAB软件，对其数学模型编写运动特性仿真程序进行模拟仿真，可得优化后机构在压紧角ψ内的滑块位移、速度、加速度曲线，如图6所示。

图6　Δs=0.015 mm时的滑块运动曲线

从图6可以看出以Δs=0.015 mm为条件经过优化后的串联四连杆机构，即在微波动量Δs比原方案减小83.7%时，压紧角ψ=97.059°，比原方案增大3.4%，最大速度vmax=0.506 mm/s，比原方案减小80.0%，最大加速度amax=10.932 mm/s2，比原方案减小75.1%。

5　结论

(1)对双动拉延机械压力机外滑块驱动机构的三种常用类型的优缺点进行了分析，指出三角摆杆式串联四连杆机构综合性能较好。

(2)对J45-315型闭式单点双动机械压力机压边滑块所使用的三角摆杆式串联四连杆工作机构进行了运动学分析，获得了外滑块的位移、速度、加速度的数学表达式。

(3)建立了J45-315型双动拉延压力机压边滑块使用的三角摆杆式串联四连杆工作机构的优化模型，并用MATLAB编制了优化程序。

(4)使用所研制的优化程序，对J45-315型双动拉延压力机使用的外滑块驱动三角摆杆式串联四连杆工作机构进行了优化，优化后的研究结果表明，外滑块位移波动量由原来的0.092 mm减小到0.015 mm，即压边外滑块位移波动量比原机构减小83.7%时，外滑块压紧角增大3.4%，有效提高了双动拉延机械压力机冲压的工作性能。

[1]耶晓东，何亚银．基于虚拟样机的拉延压力机外滑块机构运动性能研究[J]．机械设计，2013，30(7)：38-41.

Ye Xiaodong,He Yayin.Study on Motion Characteristics of Drawing Press Outer Slide Mechanisms Based on the Virtual Prototype[J]．Journal of Mechanical Design，2013，30(7)：38-41.

[2]彭玉海．基于虚拟样机的拉延压力机工作机构运动性能研究[J]．机械设计与制造，2013(3):211-213.

Peng Yuhai.Analysison the Motion Characteristics of Drawing Press Working Mechanism Based on the Virtual Prototype[J]．Machinery Design & Manufacture，2013(3):211-213.

[3]于珊珊，贺磊，郭前建．基于ADAMS软件的机械压力机工作机构优化设计[J]．机械设计，2013,30(2):24-27.

Yu Shanshan,He Lei, Guo Qianjian.Optimal Design of Working Mechanism in Mechanical Press Based on Software ADAMS[J]．Journal of Mechanical Design，2013,30(2):24-27.

[4]杨春峰，张盛，李云鹏．机械压力机六连杆机构优化设计[J]．大连理工大学学报，2013，53(1):64-70.

Yang Chunfeng,Zhang Sheng,Li Yunpeng．The Optimum Design for Six-bar Linkage of Mechanical Press[J]．Journal of Dalian University of Technology，2013，53(1):64-70.

[5]谢嘉，赵升吨，梁锦涛．压力机杆系优化求解的变量循序组合响应面法[J]．西安交通大学学报，2012,46(5)：57-62.

Xie Jia,Zhao Shengdun,Liang Jintao. Variable Sequential Combination Response Surface Methodology for Press Rod System Optimization[J]．Journal of Xian Jiaotong University，2012,46(5)：57-62.

[6]尚万峰，赵升吨．伺服压力机加工工艺的Bezier模型及其优化研究[J]．西安交通大学学报，2012,46(3)：31-35.

Shang Wanfeng,Zhao Shengdun.Servo Press Processing Bezier-model with Optimum[J]．Journal of Xi’an Jiaotong University，2012,46(3)：31-35.

[7]车林仙，何兵，程志红．扇形采样约束多目标差分进化算法及工程应用[J]．机械工程学报，2013，49(23)：150-160.

Che Linxian,He Bing,Cheng Zhihong.Sector-sampling-based Constrained Multi-objective Differential Evolution and Its Engineering Application[J]．Journal of Mechanical Engineering，2013，49(23)：150-160.

[8]李烨健，孙宇，胡峰峰．多杆高速机械压力机机构优化设计[J]．中国机械工程，2015，26(1)：31-36.

Li Yejian, Sun Yu ,Hu Fengfeng．Optimization Design for Multi-linkage of High-speed Mechanical Press[J]．China Mechanical Engineering，2015，26(1)：31-36.

[9]Kriechenbauer S,Mauermann R,Landgrebe D.Deep Drawing with Local Hardening on Digital Multi-axis Servo Press[J].Acta Metallurgica Sinica (English Letters),2015，28(12)：1490-1495.

[10]Kitayama S，Saikyo M，Kawamoto K，et al.Multi-objective Optimization of Blank Shape for Deep Drawing with Variable Blank Holder Force via Sequential Approximate Optimization[J].Structural and Multidisciplinary Optimization，2015,52(5)：1001-1012.

[11]李建，王建新，殷文齐．六连杆机械压力机传动机构优化设计[J]．一重技术,2011(1): 7-10.

Li Jian,Wang Jianxin,Yin Wenqi．Optimization Design of the Six-link Transmission Mechanism Used in Mechanical Press[J]．CFHI Technology,2011(1): 7-10.

[12]李启鹏, 刘万俊, 仝崇楼．基于SolidWorks运动仿真的平面八连杆机构优化设计[J]．机械传动, 2009, 33(1): 63-67.

Li Qipeng,Liu Wanjun,Tong Chonglou. Flat Eight-bar linkage Optimum Design based on SolidWorks Motion Simulation[J]．Journal of Mechanical Transmission, 2009, 33(1): 63-67.

[13]何德誉．曲柄压力机[M]．北京：机械工业出版社，1981．

[14]罗中华，彭炎荣．双动拉延压力机外滑块传动机构的优化设计[J]．锻压技术，1997(3):46-49.

Luo Zhonghua，Peng Yanrong.Optimum Design for Transmission Mechanism of Outer Slide in Double Action Drawing Press[J]．Forging & Stamping Technology,1997(3):46-49.

(编辑王旻玥)

Optimization of Pressure Side Slider Series Four-bar Linkage Working Mechanism Used by Double-action Press

Jia Xian1Zhao Shengdun2Fan Shuqin2Tan Shuanbin1

1.Xi’an Siyuan University,Xi’an,710038 2.Xi’an Jiaotong University,Xi’an,710049

Concerning the side-pressing effects and large displacement variations in outer sliders conducting side-pressing action by unreasonable lengthes and angles of truss system in J45-315 closed single-point and double-acting drawing press, an optimized mathematical model of the organization was built by using step-length searching method to optimize the variations of displacement shifts. After optimization, the variations are deduced from 0.092 mm to 0.015 mm, which means the pressing angle adds 3.4% while the variation is decreased to 83.7% of the original. The stamping property of double-acting mechanical press can be effectively increased and it lays a foundation for the optimization of working organizations when double-acting mechanical press conducts side-pressing action driven by outer sliders.

double-action drawing mechanical press; series four-bar linkage working mechanism; motion characteristics

2016-01-13

国家自然科学基金资助项目(51335009，51305333)；陕西省教育厅科研计划资助项目(12JK1069)

TG315

10.3969/j.issn.1004-132X.2016.09.014

贾先，女，1971年生。西安思源学院工学院讲师，副院长。主要研究方向为机械传动及其动态特性。赵升吨(通信作者)，男，1962年生。西安交通大学机械工程学院教授、博士研究生导师。范淑琴，女，1977年生。西安交通大学机械工程学院讲师。谭栓斌，男，1970年生。西安思源学院工学院高级工程师。