识别黏弹性阻尼材料力学参数用约束阻尼试件设计方法
2016-09-05吕振华顾叶青
王 超 吕振华 顾叶青
1.南京电子技术研究所,南京,210039 2.清华大学,北京,100084
识别黏弹性阻尼材料力学参数用约束阻尼试件设计方法
王超1吕振华2顾叶青1
1.南京电子技术研究所,南京,2100392.清华大学,北京,100084
悬臂梁弯曲共振法识别刚度较低的黏弹性阻尼材料力学参数的实验中常以约束阻尼结构试件为实验对象,试件设计的合理程度直接关系到材料力学参数的测试精度。为了更好地指导试件设计,根据灵敏度分析法提出了影响系数的概念,并将其应用于分析试件的厚度比、共振频率比、密度比、损耗因子等参数的测量误差对黏弹性材料力学参数测试精度的影响中,进而为试件的设计提供了一些有重要工程价值的技术指标。最后,基于悬臂梁弯曲共振法实验理论,分析得到适合使用约束阻尼结构试件识别其力学参数的黏弹性阻尼材料。
黏弹性阻尼材料;试件设计;灵敏度分析;影响系数;约束阻尼结构
0 引言
大多数车身结构都是薄钢板焊接结构,其阻尼损耗因子通常只能达到5×10-3左右[1]。因此,车身薄板结构通常还需要附加黏弹性阻尼材料(简称阻尼材料),以衰减来自动力总成、传动系统、悬架系统等的振动能量,从而减少车身结构的振动和噪声。
对于普通轿车,通常至少需要10~15 kg的结构阻尼材料用于减振降噪,而对于某些高级轿车,阻尼材料的用量可达30 kg[2]。为了实现轻量化和动态舒适性的双重要求,就需要对车身薄板上附加的结构阻尼进行优化设计。因此,精确获取阻尼材料的力学参数是对其进行合理化设计的基础。
识别阻尼材料力学参数的方法主要有动态机械分析(dynamic mechanical analysis, DMA)法[3]和悬臂梁弯曲共振法[4-5],但也有通过有限元法和模态应变能法相结合来获取阻尼材料的力学参数,但这种方法只能较准确地获取中高频段(100~2500 Hz)内阻尼材料的力学参数[6]。车身上常用的某些约束阻尼材料弹性较差且刚度较低,这类材料制成的试件在DMA法测试中易发生断裂或不便于夹持,该情况下悬臂梁弯曲共振法将是仅有的选择。同时,悬臂梁弯曲共振法因其理论成熟、设备通用性好且测试精度较高而得到广泛的应用。如Caracciolo等[7]根据Oberst梁理论设计了一种阻尼材料动态力学参数自动测试系统,该系统具有较高的测试精度,但存在测试系统比较复杂、低频测试精度较低的问题。
悬臂梁弯曲共振法主要通过调节试件的规格参数(长度、厚度、基体材料等)来识别不同频率下阻尼材料的力学参数,但由于测试理论及设备的限制,试件的设计有许多约束条件,对试件的设计方法进行研究,可避免试件制作的盲目性,提高实验的测试精度。关于弯曲共振法用试件设计方法的研究较少,胡卫强等[8-9]通过分析提出了单边自由阻尼结构试件的设计中应注意的一些问题,并研究了基础梁阻尼对实验结果精度的影响。文献[10-11]对约束阻尼结构试件的设计方法进行了简单探讨。研究者虽对阻尼结构试件的设计提出了若干建议,有一定的指导意义,但其给出的设计建议相对零散,没有指出试件设计中需重点关注的一些共性指标,不便于应用。
约束阻尼结构试件适用于识别某些刚度较低且重点关注其剪切刚度的阻尼材料,同时该试件因其结构简单、便于测试等优点而被广泛应用于悬臂梁弯曲共振法实验中。本文通过灵敏度分析法对约束阻尼结构试件的设计方法进行理论分析,得出试件设计过程中需重点关注的多个指标,且试件设计的各项要求间是相互关联且相对统一的,在试件设计中应重点关注这些共性要求,进而为试件的设计提供便利。
1 基本理论
1.1弯曲共振法识别阻尼材料剪切模量和损耗因子的基本理论
通过弯曲共振法实验可测得图1所示的约束阻尼结构试件的共振频率f及对应阶次的损耗因子η,进而根据ASTM E756-05[4]求得阻尼材料的剪切模量G2和损耗因子ηv:
(1)
(2)
α=(f/f1)2(2+Dh)A=αB/2
其中,未说明的参数的含义参见文献[4]。

图1 约束阻尼结构试件
可见,阻尼材料的剪切模量G2是复合梁与基础梁对应阶次频率比(f /f1)、密度比D(D=ρ2/ρ1)、厚度比h(h=H2/H1)、复合梁损耗因子η、基础梁弹性模量E1、试件长度L、基础层厚度H1的函数;阻尼材料的损耗因子ηv是f /f1、D、h、η的函数。
1.2试件参数测量误差对力学参数测试精度影响的理论分析
试件的厚度比h、共振频率比f /f1、密度比D及损耗因子η等参数的测量误差对实验结果测试精度的影响程度是有差异的,因此,在试件设计时须先明确各试件参数的测量误差对阻尼材料力学参数测试精度的影响,以便在设计试件时确定合适的参数。下面采用灵敏度分析法研究各试件参数测量误差对力学参数测试精度的影响。
对式(1)和式(2)进行变分,并将各变量予以归一化以消除各变量的数值差异:
(3)
(4)
由式(3)和式(4)可知,E1、f /f1、D、h等参数的测量精度直接关系到阻尼材料剪切模量G2和损耗因子ηv的测试精度,故引入影响系数的概念来评价各变量的测量误差对力学参数测试精度的影响,各参数的影响系数如下:
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
P=A-B-2(A-B)2-2(Aη)2
R=(1-2A+2B)2+4(Aη)2
2 通过影响系数法分析各试件参数测量误差对测试精度的影响
本文主要采取以下思路研究试件参数测量误差对悬臂梁弯曲共振法实验测试精度的影响:首先,以基础层和约束层的材料是钢材的约束阻尼结构试件为研究对象,阻尼材料的密度取ρ2= 1.0×103kg/m3,复合梁结构的损耗因子取η=0.4,通过影响系数法分析各试件参数的测量误差对实验结果测试精度的影响。然后,进一步研究阻尼材料的密度(密度比)和复合梁结构的损耗因子等参数对各影响系数的影响。最后得出普遍适用的便于指导约束阻尼结构试件设计的结论。
2.1试件参数测量误差对阻尼材料剪切模量测试精度的影响


1.h=0.05 2.h=0.10 3.h=0.20 4.h=0.30图随频率比f/f1的变化
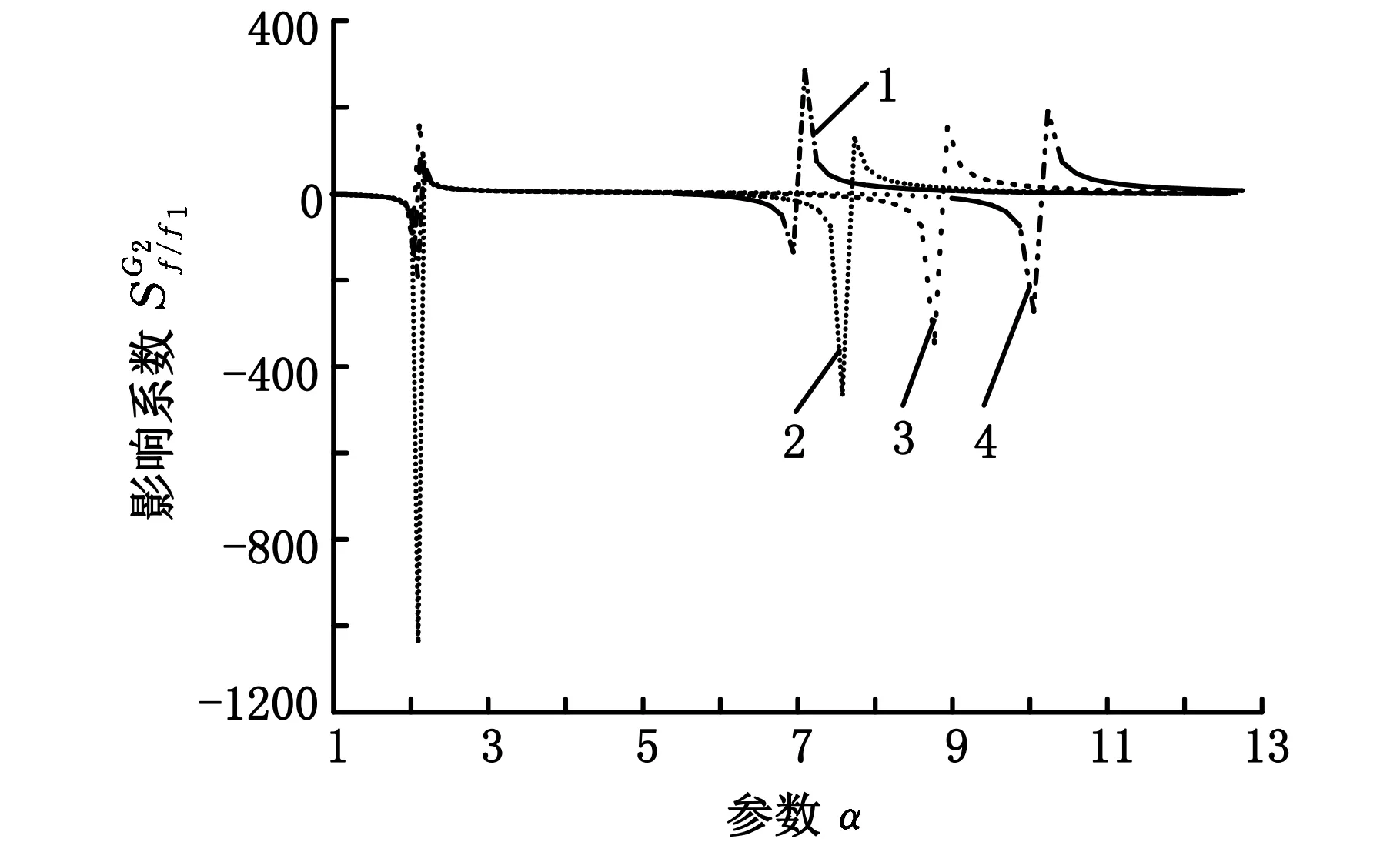
1.h=0.05 2.h=0.10 3.h=0.20 4.h=0.30图f/f1随参数α的变化

1.h=0.05 2.h=0.10 3.h=0.20 4.h=0.30图随频率比f/f1的变化

1.h=0.05 2.h=0.10 3.h=0.20 4.h=0.30图D随参数α的变化


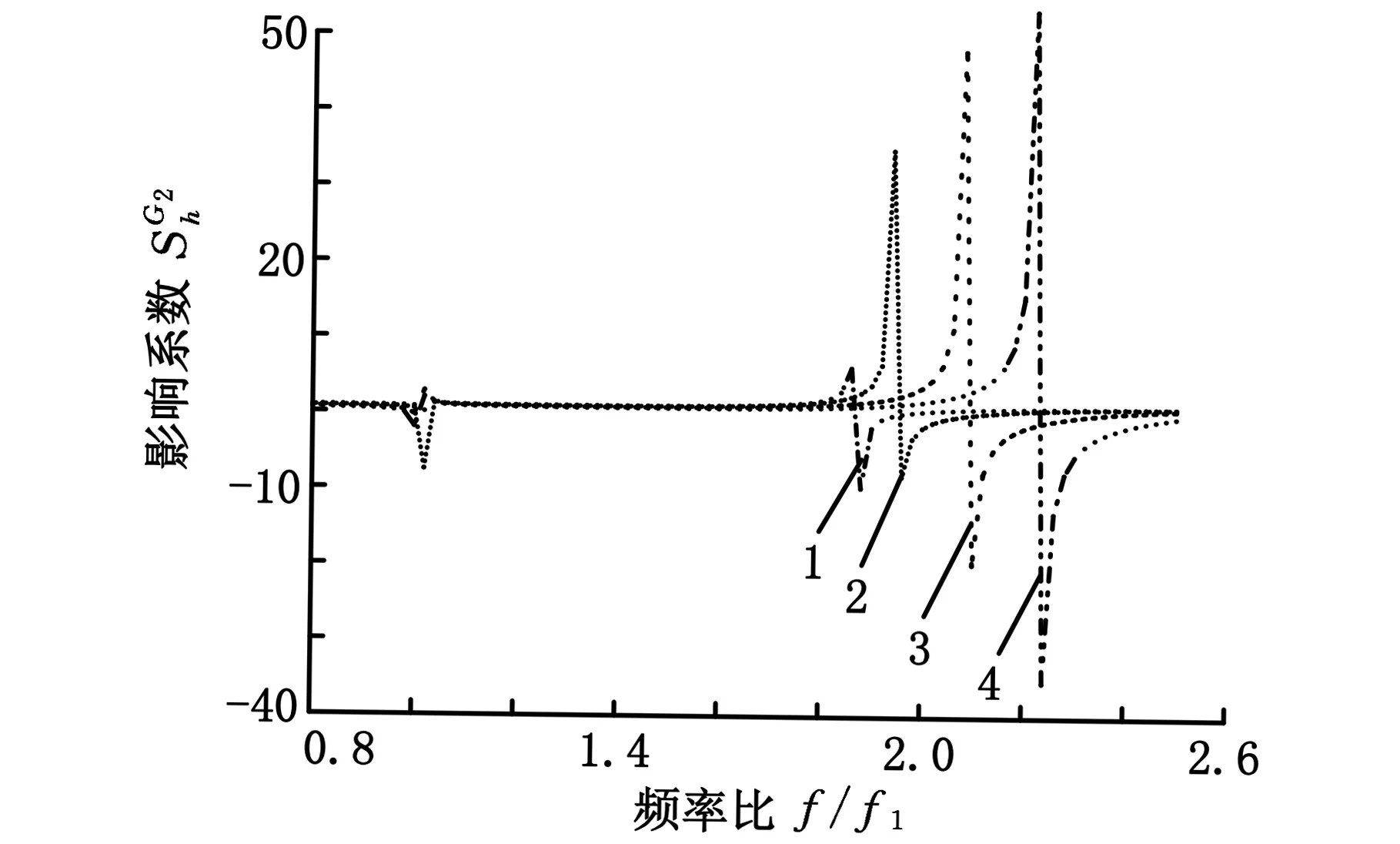
1.h=0.05 2.h=0.10 3.h=0.20 4.h=0.30图随频率比f/f1的变化

1.h=0.05 2.h=0.10 3.h=0.20 4.h=0.30图h随参数α的变化


1.h=0.05 2.h=0.10 3.h=0.20 4.h=0.30图随频率比f/f1的变化

1.h=0.05 2.h=0.10 3.h=0.20 4.h=0.30图η随参数α的变化



1.h=0.05 2.h=0.10 3.h=0.20 4.h=0.30图随频率比f/f1的变化

1.h=0.05 2.h=0.10 3.h=0.20 4.h=0.30图H1随参数α的变化
2.2试件参数测量误差对阻尼材料损耗因子测试精度的影响

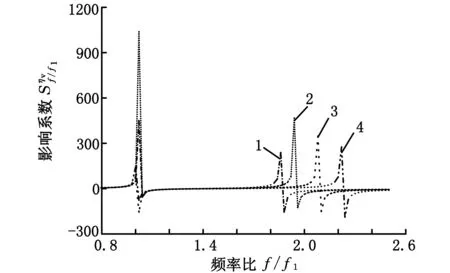
1.h=0.05 2.h=0.10 3.h=0.20 4.h=0.30图随频率比f/f1的变化
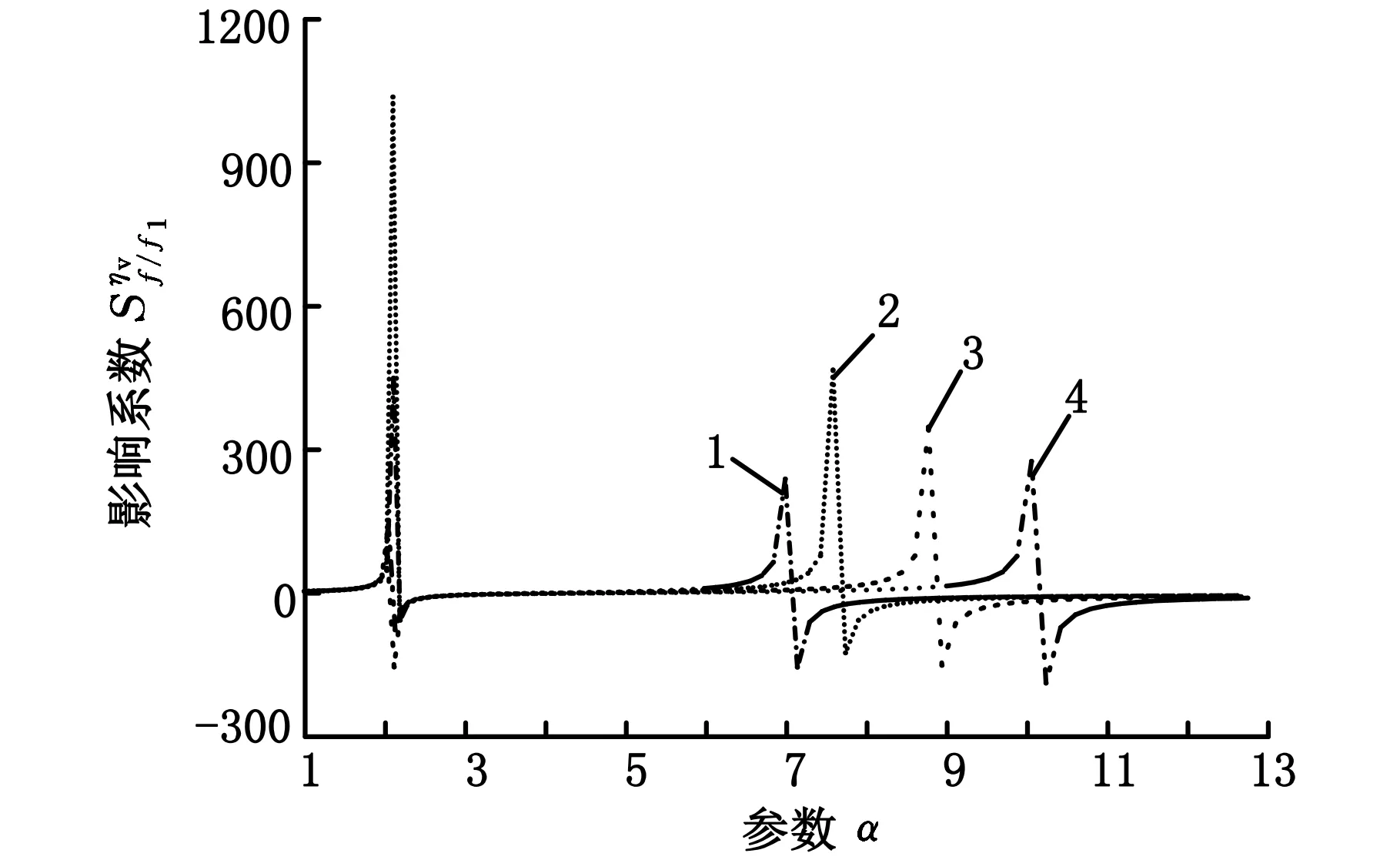
1.h=0.05 2.h=0.10 3.h=0.20 4.h=0.30图f/f1随参数α的变化

1.h=0.05 2.h=0.10 3.h=0.20 4.h=0.30图随频率比f/f1的变化

1.h=0.05 2.h=0.10 3.h=0.20 4.h=0.30图D随参数α的变化


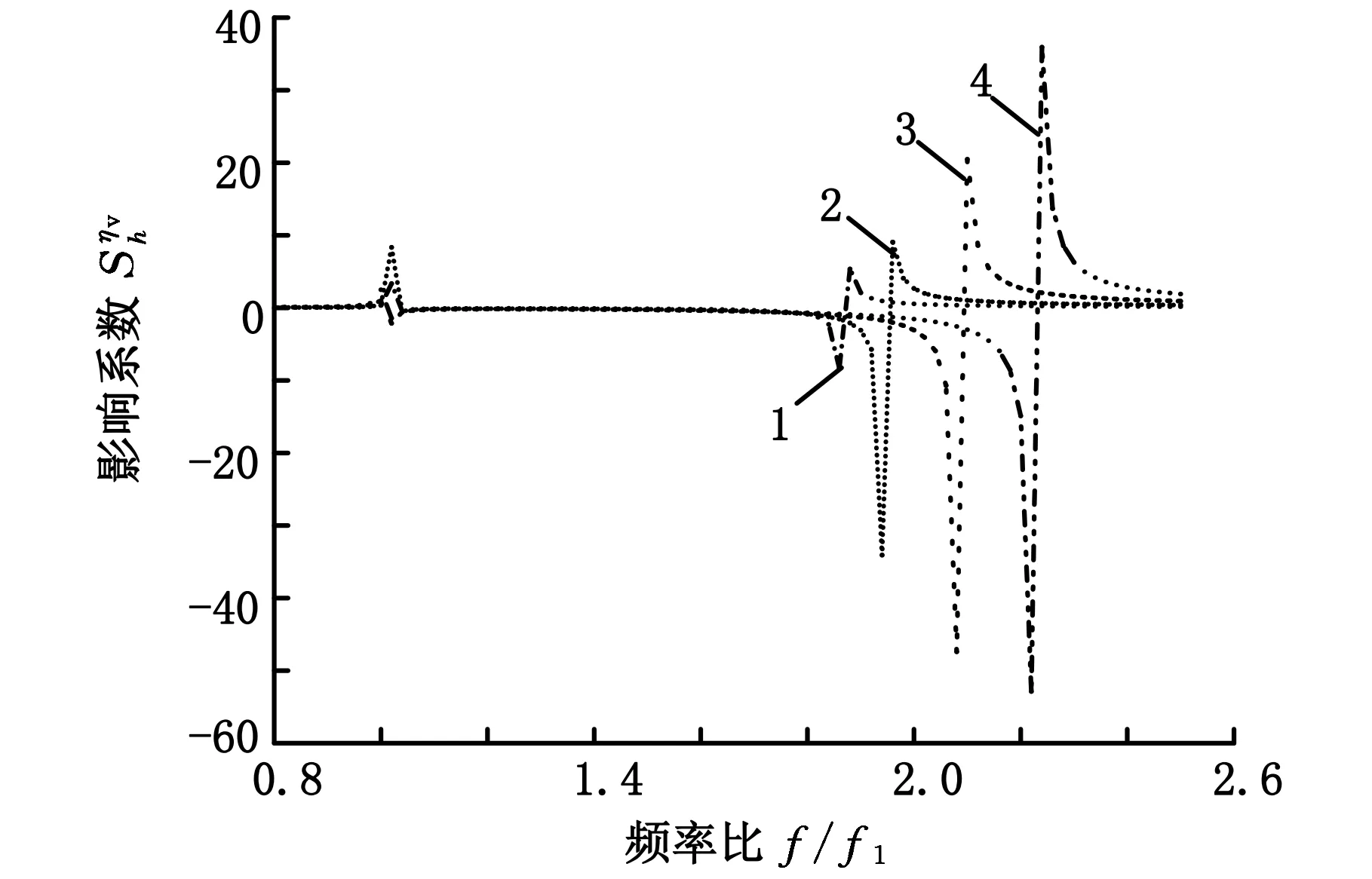
1.h=0.05 2.h=0.10 3.h=0.20 4.h=0.30图随频率比f/f1的变化

1.h=0.05 2.h=0.10 3.h=0.20 4.h=0.30图h随参数α的变化


1.h=0.05 2.h=0.10 3.h=0.20 4.h=0.30图随频率比f/f1的变化

1.h=0.05 2.h=0.10 3.h=0.20 4.h=0.30图η随参数α的变化
2.3各参数测量误差对实验结果测试精度的影响分析
由图2~图19可以得出:各影响系数随参数α的变化规律均表明,在α=2附近时各系数均有很大的幅值,说明ASTM中规定α≥2.01有一定的合理性,但通过前述分析得到各影响系数随α的变化规律,认为α≥2.2更为合理,且应同时满足α≤6;在满足2.2≤α≤6的条件下,制作试件时应使其频率比f/f1尽量偏离1。由于实际情况下采用的是对称约束阻尼结构,所以一般情况下f/f1>1,但在稍高阶次的振动下频率比f/f1近似等于1,进而产生较大的测试误差;实验中应尽可能精确测量频率比f/f1,因为该参数的测试误差对实验结果测试精度的影响比其他因素大得多;基础层弹性模量E1以及悬臂梁的长度L的测量误差对测试精度的影响最小且保持不变。
3 讨论
3.1阻尼材料密度对测试精度的影响


(a)频率比不同的情况下

(b)参数α不同的情况下图20 密度比对影响系数D变化规律的影响
3.2复合梁试件损耗因子对测试精度的影响


(a)频率比不同的情况下
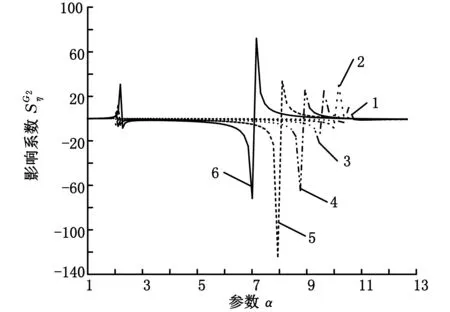
(b)参数α不同的情况下1.η=0.1 2.η=0.2 3.η=0.34.η=0.4 5.η=0.5 6.η=0.6图21 复合梁结构损耗因子对影响系数η变化规律的影响
3.3试件频率比的合理范围
前述分析表明,当2.2≤α≤6时,利用附加约束阻尼层的复合梁试件测试阻尼材料的力学参数具有较高的精度。图22和图23所示为满足该条件的试件的厚度比与其频率比应满足的关系。
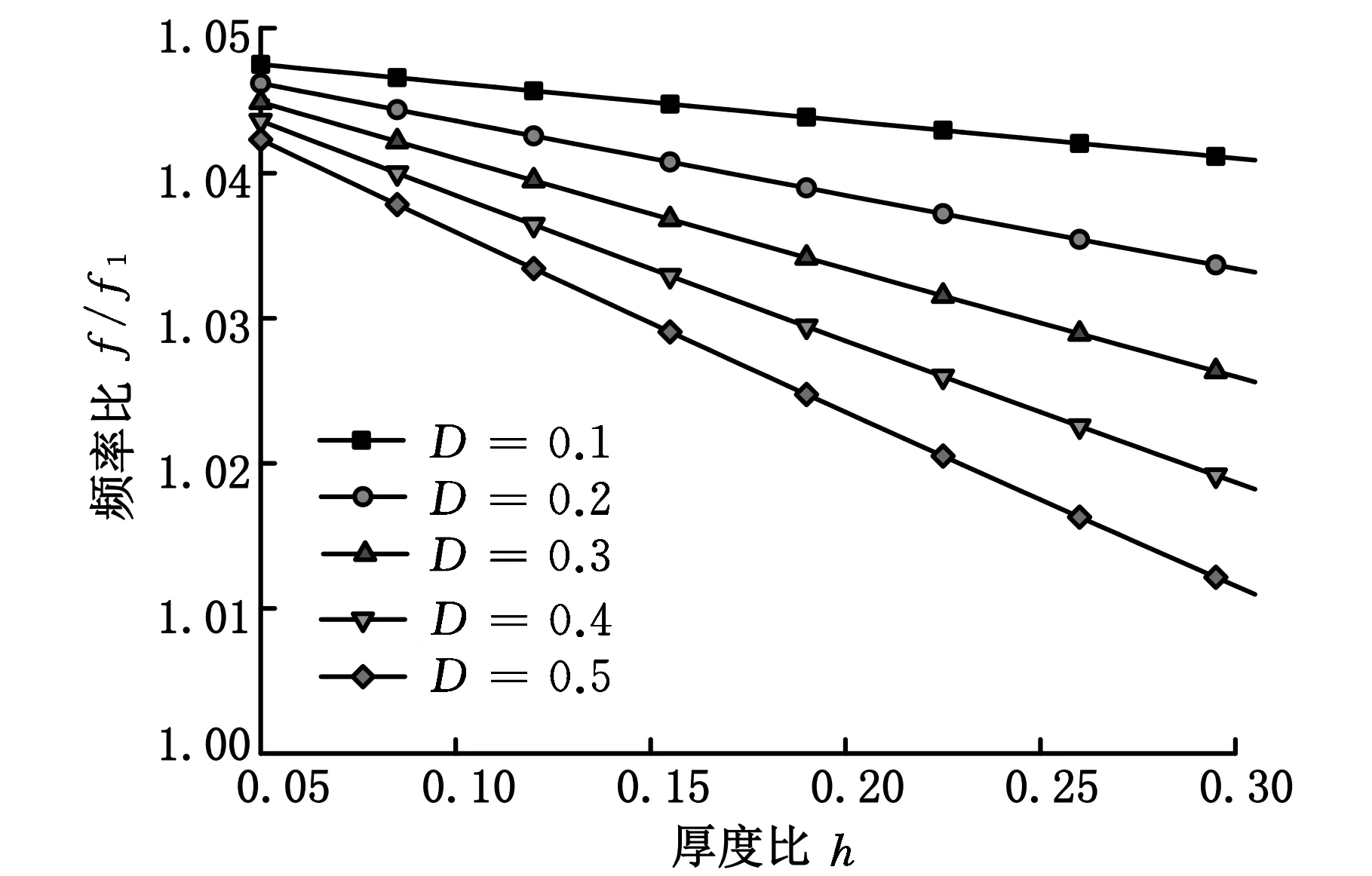
图22 厚度比h对应的f/f1下限

图23 厚度比h对应的f/f1上限
4 结论
(1)根据灵敏度分析法提出的影响系数法研究了各试件参数测量误差对实验结果测试精度的影响。各影响系数随参数α的变化规律均表明,在参数α=2附近和α>6的某一范围内各影响系数均会出现峰值,试件设计时应使参数α满足2.2≤α≤6,并将此要求作为约束阻尼结构试件设计时须首先遵循的技术要求。
(2)各试件在参数α满足2.2≤α≤6的条件下,应使其频率比f/f1满足图22和图23所示的上下限值的要求,这样才可以保证有较高的测试精度。
(3)实验中应尽可能准确地测量频率比f/f1,因为由此产生测量结果的误差比厚度比h、密度比D等其他参数的影响大很多。
(4)基础层和约束层材料的弹性模量E1及试件的长度L的测量误差对测试精度的影响最小且保持不变。
(5)复合梁结构试件的损耗因子η和密度比D的变化不影响各影响系数随频率比f/f1和参数α的变化规律。
[1]庞剑,谌刚,何华. 汽车噪声与振动——理论与应用[M]. 北京:北京理工大学出版社,2006.
[2]戴德沛. 阻尼技术的工程应用[M]. 北京:清华大学出版社,2004.
[3]GJB 981-1990.黏弹性阻尼材料强迫非共振型动态测试方法[S].北京:中国标准出版社,1991.
[4]ASTM E756-05. Standard Test Method for Measuring Vibration Damping Properties of Materials[S]. New York :American National Standards Institute, 2010.
[5]GB/T 16406-1996.声学材料阻尼性能的弯曲共振测试方法[S]. 北京:中国标准出版社,1996.
[6]Ghiringhelli G L, Terraneo M. Analytically Driven Experimental Characterization of Damping in Viscoelastic Materials[J]. Aerospace Science and Technology, 2015, 40: 75-85.
[7]Caracciolo R, Gasparetto A, Giovagnoni M. An Experimental Technique for Complete Dynamic Characterization of a Viscoelastic Material[J]. Journal of Sound and Vibration, 2004, 272(3/5): 1013-1032.
[8]胡卫强,王敏庆,刘志宏. 悬臂梁弯曲共振法自由阻尼结构试件设计研究[J]. 实验力学,2008, 23(3): 241-247.
Hu Weiqiang, Wang Minqing, Liu Zhihong. Study of the Design of Free-damping form Specimen in Resonance Method[J]. Journal of Experimental Mechanics, 2008, 23(3): 241-247.
[9]胡卫强,王敏庆,刘志宏. 基底层阻尼对悬臂梁弯曲共振法测量结果的影响分析[J]. 振动与冲击, 2008, 27(6):170-172.
Hu Weiqiang, Wang Minqing, Liu Zhihong. Influence of Based-beam Damping on Test Results of Resonance Method[J]. Journal of Vibration and Shock, 2008, 27(6):170-172.
[10]马少璞,王敏庆,胡卫强,等.对称夹层结构的共振梁法理论误差研究[J]. 噪声与振动控制, 2008, 28(4):38-41.
Ma Shaopu, Wang Minqing, Hu Weiqiang, et al. Study on Theoretical Error of the Resonance Beam Testing Method about Sandwich Specimen[J]. Journal of Noise and Vibration Control, 2008, 28(4):38-41.
[11]朱蓓丽,沈庆元. 黏弹性材料复剪切模量的测量及误差分析[J]. 噪声与振动控制, 1999(6):38-41.
Zhu Beili, Shen Qingyuan. Measurement of the Viscoelastic Material’s Complex Shear Modulus and the Error Analysis[J]. Journal of Noise and Vibration Control, 1999(6):38-41.
(编辑陈勇)
Design Methods of Constrained Damping Specimen Used in Measurement of Viscoelastic Damping Material’s Mechanics Parameters
Wang Chao1Lü Zhenhua2Gu Yeqing1
1.Nanjing Research Institute of Electronics Technology,Nanjing,210039 2.Tsinghua University,Beijing,100084
The sandwich specimens with supplemental structural damping were frequently used in the measurement of mechanics parameters of viscoelastic material with low stiffness through flexural resonating cantilever beam method (FRCBM), so appropriate designed specimens might assure the accuracy of experimental results. Through sensitivity analysis, influence coefficient was proposed and used in the precision analysis of experimental results which were affected by the measurement accuracy of thickness ratio, resonance frequency ratio, density ratio and loss factor of the specimen, and some significant technical specifications were proposed to help design specimens. Finally, the applicability of the sandwich specimens used in the measurement of viscoelastic material’s mechanics parameters through FRCBM was analyzed.
viscoelastic material; specimen design; sensitivity analysis; influential coefficient; constrained damping structure
2015-07-14
国家高技术研究发展计划(863计划)资助项目(2006AA110103);国家自然科学基金资助项目(51490664)
U465.4;TQ317.3
10.3969/j.issn.1004-132X.2016.09.012
王超,男,1984年生。南京电子技术研究所工程师、博士。主要研究方向为汽车振动特性分析与优化设计方法、大型相控阵雷达阵面结构设计方法。吕振华,男,1961年生。清华大学汽车工程系汽车安全与节能国家重点实验室教授、博士研究生导师。顾叶青,男,1979年生。南京电子技术研究所高级工程师。
