基于Kriging代理模型的结构损伤识别新方法

郭俊龙　马立元　李永军　王天辉

军械工程学院，石家庄，050003



基于Kriging代理模型的结构损伤识别新方法

郭俊龙马立元李永军王天辉

军械工程学院，石家庄，050003

提出一种基于Kriging代理模型的损伤识别方法。利用初始样本建立结构响应与结构损伤参数之间的关系，代替原结构响应与结构物理参数之间的关系，有效减少损伤识别过程中反复调用有限元软件对结构进行网格划分和有限元计算的次数，提高了识别效率。采用加点准则对代理模型进行修正，保证代理模型可以准确反映结构响应与结构损伤参数之间的关系。通过一个管梁结构的数值算例验证了所提方法的有效性。最后，将该方法应用于某导弹发射台模型的损伤识别中，实验结果表明，该方法可应用于工程实际。

损伤识别；Kriging代理模型；大型复杂结构；程度识别

0　引言

近年来，基于有限元模型修正的结构损伤识别方法得到广泛的关注，并取得了许多成果[1-2]。目前，有限元模型修正方法主要分为两类[3]：一类为矩阵型模型修正方法[4]；一类为参数型模型修正方法[5]。这两类方法所得模型的精度受诸多因素影响，难以达到很高的精度。基于模型修正的损伤识别方法识别结果依赖于初始有限元模型的精度，这样将导致识别结果的不准确，而且损伤识别过程需要进行大量有限元计算，效率很低。

代理模型是一种可以跳过复杂的有限元计算过程，而直接构造结构动态响应与结构损伤参数之间关系的简化模型。常用的代理模型有RSM(响应面法)代理模型、RBF(径向基函数)代理模型、Kriging(克立格)代理模型等。很多学者将响应面模型应用到模型修正中[6]，并取得了较好的效果。但响应面法在解决多局部极值问题时易陷入局部最优，而且构建响应面模型需要大量的样本点，这在一定程度上降低了损伤识别的效率。而Kriging代理模型是基于Kriging插值技术的一种等效模型，它根据样品空间位置的不同和样品间相关程度的不同，对每个样品的品位赋予一定的权值，进行滑动加权平均，以此估计某一未知点的品位。Kriging代理模型不仅考虑了待估点位置与已知数据位置的相关关系，而且还考虑了变量的空间相关性[7]，因此仅需少量样本便能准确描述系统响应与系统输入之间的关系，常被用于金属矿探测[8]以及结构的优化设计[9]和结构稳健性设计[10]，但在损伤识别领域的应用还比较少见。

本文将Kriging代理模型应用到大型复杂结构的损伤识别中，使用Kriging代理模型代替原有复杂的有限元模型，简化了复杂的有限元网格划分和计算过程，提高了损伤识别效率。

1　Kriging代理模型

Kriging代理模型包括回归部分和非参数部分，因此该模型由多项式和随机分布两部分组成，则某一未知点x的预测响应为

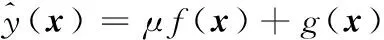
(1)

其中，f(x)为回归模型，是关于损伤变量的多项式，在设计空间中，提供模拟损伤与动态响应的全局近似，可以是常数、一阶多项式或二阶多项式等；μ为回归系数；g(x)为代理模型的估计误差，是一个随机过程，其均值为0，方差为σ2，协方差矩阵中的元素可表示为

C[g(xi),g(xj)]=σ2R(θ,xi,xj)i,j=1,2,…,n

(2)

xi=[xi1xi2…xim]

式中，xi为关于损伤的第i个样本，包含损伤的位置、程度等；R(θ,xi,xj)为任意两样本点xi、xj之间的带有参数θ的空间相关函数，决定了代理模型的精度；n为样本点数。

由此可见，构建Kriging代理模型的关键是回归系数μ和方差σ2的确定。

设样本点组X={x1,x2,…,xn}对应的结构响应为Y={y(x1),y(x2),…,y(xn)}，则回归系数μ和方差σ2可估计为

(3)

(4)

F=[f(x1)f(x2)…f(xn)]T

R为各样本点之间的空间相关函数矩阵，即：

(5)

在求得θ值后，进行回代，便可完成Kriging代理模型的构造过程。MATLAB中提供了Kriging代理模型的工具箱DACE，可通过编写相应程序获得结构响应的Kriging代理模型。

此时，某一未知点x的估计响应值为

(6)

r(x)=[R(θ,x1,x)R(θ,x2,x)…R(θ,xn,x)]

式中，r(x)为未知点与各个已知样本点的相关函数向量。

针对不同情况，可选取不同相关函数。本文所选相关函数为

(7)

式(6)即为用Kriging代理模型替代原有有限元模型后结构响应与损伤参数之间的关系。

为了评价Kriging代理模型对未知点预估能力的准确性，采用平方相关系数准则γSC和平方误差准则γEISE进行验证：

(8)

(9)

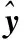
如果代理模型预测的响应不能满足以上准则，则需要通过加点准则进行修正，本文选用多点加点准则[11]对Kriging代理模型进行修正。

2　基于Kriging代理模型的损伤识别步骤

成功构建结构的Kriging代理模型后，则结构损伤识别问题转化为多目标优化问题，即在一定的搜索区域内，寻求一组损伤参数值，使得实际测得的结构响应与Kriging代理模型预估的结构响应误差最小，从而识别出损伤。由此构建目标函数如下：

(10)

具体识别过程如下：

(1)应用有限元软件构建结构的有限元模型，并进行修正，得到修正后结构的精准有限元模型；

(2)采用拉丁超立方方法抽取若干组损伤参数值作为样本，并通过有限元软件计算对应损伤状况下的结构响应；

(3)利用样本与其对应的响应构建结构的Kriging代理模型，得到结构输出响应与损伤参数之间的关系；

(4)针对待识别工况的响应，通过优化算法搜寻一组损伤参数值使得目标函数达到最小值，同时通过式(8)、式(9)验证Kriging代理模型的准确性(γSC>0.99，γEISE<0.01)；

(5)若Kriging代理模型满足以上准则，则此时的损伤参数值即为待识别工况的实际损伤情况，否则，需要通过加点准则对Kriging代理模型进行修正；

(6)重复步骤(4)、步骤(5)，直至Kriging代理模型满足准确性准则，则可求得对应待识别工况下的损伤参数值。

为了验证上述方法，本文首先通过一个数值算例验证该方法的有效性，随后将该方法应用于某导弹发射台模型的损伤识别研究中，证明其在工程实际应用中的可行性。

3　数值算例

某管梁结构示意如图1所示，其长度为0.70m，外径50mm，内径40mm，材料弹性模量E=207GPa，泊松比ν=0.27，密度ρ=7800kg/m3，结构为瑞利阻尼，结构一端简支，一端铰支。通过ANSYS软件建立有限元模型，有限元建模中，单元类型选用Beam189单元，将结构划分为20个单元，21个节点。一般认为结构的损伤表现为单元刚度的降低，单元质量保持不变，ANSYS有限元分析中，通过材料弹性模量的折减来模拟单元刚度的降低。

图1　管梁有限元模型

首先抽取20个损伤样本建立结构响应与损伤参数之间的Kriging代理模型，并依据加点准则对模型进行修正，得到修正后的Kriging代理模型。对4种工况进行损伤识别，各损伤工况参数如表1所示(括号内为损伤单元编号)。

表1　损伤工况

设置完损伤后，首先通过有限元分析方法计算出对应的结构响应，然后使用多族群粒子群优化算法对目标函数进行优化，族群个数设为2，群规模为20，粒子搜索维度为5，搜索范围为(0，1)，通过调整损伤位置和损伤程度的相关参数使目标函数取得最小值，得到识别结果如表2所示(括号内为损伤单元编号)。

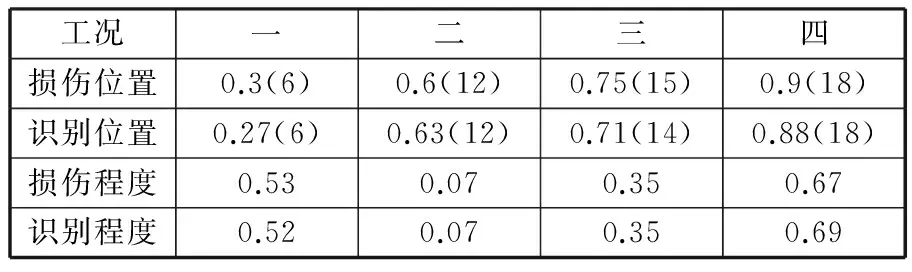
表2　损伤识别结果

从识别结果可以看出，通过Kriging代理模型可以基本确定损伤位置，而且对损伤程度也有较好的识别效果。图2所示为结构前4阶固有频率与损伤参数间Kriging代理模型的响应面。

4　实验验证

某导弹发射台骨架模型如图3所示，该结构由9根钢管和两个连接耳片焊接组成，材料为Q235钢。左右弯管直径为60mm，其余钢管直径为48mm，钢管壁厚5mm。

(a)第一阶频率

(b)第二阶频率

(c)第三阶频率

(d)第四阶频率图2　前4阶模态频率Kriging代理模型响应面

图3　发射台骨架模型

建立其有限元模型，如图4所示，有限元建模时选用beam189单元，模型包含138个梁单元和271个节点。建立好结构初始有限元模型后，需要对其进行模型修正，获得结构的精准有限元模型。之后，建立结构的Kriging代理模型并进行损伤识别。

图4　发射台骨架结构有限元模型

通过拉丁超立方方法获得50组损伤样本，利用ANSYS软件计算各损伤对应的响应，建立发射台骨架模型的Kriging代理模型，验证Kriging代理模型的准确性并依据加点准则进行修正，得到结构响应与损伤参数之间的关系，即为修正后的发射台骨架Kriging代理模型。

得到发射台骨架的Kriging代理模型后，在发射台骨架模型上设置真实损伤进行损伤识别，损伤通过在发射台骨架上方直管左侧1/4处(第79号单元)锯裂缝的方式进行设置，如图5所示，具体情况见表3。

(a)工况一　　　　(b)工况二(c)工况三图5　发射台骨架实验工况设置

工况一二三裂缝深度(cm)1.02.03.0等效刚度折减0.150.260.43

为了表征损伤程度，通过有限元模型修正方法获得单元79处裂缝深度为1cm、2cm、3cm时对应的结构损伤处刚度折减分别为15%、26%、43%。

首先在发射台骨架上通过力锤敲击的方式施加脉冲激励，使用江苏东华公司生产的DH5920动态信号测试分析仪及其配套软件对结构进行试验数据采集和模态分析，得到结构的模态频率和模态振型，然后利用建立好的发射台骨架Kriging代理模型，使用多族群粒子群优化算法进行优化识别，族群个数设为5，族群规模为20，搜索维度为10，搜索范围为(0，1)，通过调整代理模型中的损伤参数使目标函数取得最小值，得到对应的识别结果，如表4所示。

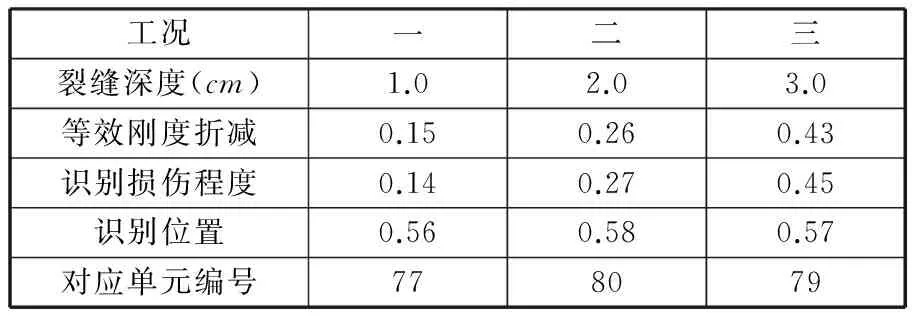
表4　损伤识别结果

由表4识别结果可以看出，虽然实际工程应用中存在噪声等不利因素的影响，但本文所提方法仍可有效确定损伤位置和损伤程度，且识别精度较高。

5　结论

(1)Kriging代理模型可以准确描述结构响应与结构损伤参数之间的关系，能够有效替代原有结构响应与结构物理参数之间的关系。

(2)基于Kriging代理模型的损伤识别方法可有效确定结构损伤位置和损伤程度，且识别精度较高。

(3)使用Kriging代理模型可以避免在损伤识别过程中进行复杂的有限元计算，简化了计算过程，提高了损伤识别的效率。

特别指出，本文是在假定损伤个数的前提下进行损伤识别研究的，针对损伤个数的确定问题，笔者已另文详述。

[1]钟儒勉，宗周红，秦中远，等. 基于多尺度模型修正的结合梁斜拉桥损伤识别方法[J]. 东南大学学报(自然科学版), 2014,44(2):350-356.

ZhongRumian,ZongZhouhong,QinZhongyuan，etal.DamageIdentificationMethodofCompositeCable-stayedBridgeBasedonMulti-scaleModelUpdating[J].JournalofSoutheastUniversity(NaturalScienceEdition), 2014,44(2):350-356.

[2]PereraR,FangSE,HuertaC.StructuralCrackDetectionwithoutUpdatedBaselineModelbySingleandMultiobjectiveOptimization[J].MechanicalSystemsandSignalProcessing, 2009,23(3):752-768.

[3]胡俊亮，颜全胜，郑恒斌，等. 基于Kriging模型的钢管混凝土连续梁拱桥有限元模型修正[J]. 振动与冲击.2014,33(14):33-39.

HuJunliang,YanQuansheng,ZhengHengbin,etal.CFSTArch/continuousBeamBridgeFEMModelUpdatingBasedonKrigingModel[J].JournalofVibrationandShock, 2014,33(14):33-39.

[4]向锦武, 周传荣, 张阿舟.基于建模误差位置识别的有限元模型修正方法[J]. 振动工程学报,1997,10(1):1-6.

XiangJinwu,ZhouChuanrong,ZhangAzhou.ModificationofFiniteElementModelBasedonIdentifiedErrorLocations[J].JournalofVibrationEngineering, 1997,10(1):1-6.

[5]李伟明, 洪嘉振. 基于频响函数的模型修正方法[J].上海交通大学学报,2011,45(10):1455-1459.

LiWeiming,HongJiazhen.ResearchonModelUpdatingMethodBasedonFrequencyResponseFunctions[J].JournalofShanghaiJiaotongUniversity, 2011,45(10):1455-1459.

[6]马立元, 李世龙, 王维峰, 等. 大型复杂钢管焊接结构损伤识别方法研究[J]. 中国机械工程, 2014, 25(18): 2478-2483.

MaLiyuan,LiShilong,WangWeifeng,etal.StudyonDamageIdentificationMethodsofLargeandComplexSteelTubeWeldedStructures[J].ChinaMechanicalEngineering, 2014,25(18):2478-2483.

[7]KrigeDG.AStatisticalApproachtoSomeBasicMineValuationProblemsontheWitwatersrand[J].JournaloftheChemecal,MetallurgicalandMiningSocietyofSouthAfrica,1951,52:119-139.

[8]邢红星, 琚太忠, 林建阳.普通克里格法在矿产储量计算中的应用[J]. 地质与勘探, 1997(4):46-51.

XinHongxing,JuTaizhong,LinJianyang.TheOrdinaryKriging’sApplicationtoMineralCalculationofReserves[J].GeologyandProspecting, 1997(4):46-51.

[9]肖立峰,张广泉,张以都. 基于Kriging代理模型的结构形状优化方法[J]. 机械设计, 2009,26(7):57-60.

XiaoLifeng,ZhangGuangquan,ZhangYidu.OptimizationMethodofStructuralShapeBasedonKrigingSurrogateModel[J].JournalofMachineDesign, 2009,26(7):57-60.

[10]陈永亮,刘双,王汉涛, 等.基于Kriging代理模型的主轴箱稳健设计[J]. 天津大学学报,2011,44(12):1111-1117.

ChenYongliang,LiuSuang,WangHantao,etal.RobustDesignofHeadstockBasedonKrigingSurrogateModel[J].JournalofTianjinUniversity, 2011,44(12):1111-1117.

[11]高月华,王希诚.基于Kriging代理模型的多点加点序列优化方法[J]. 工程力学,2012,29(4):90-95.

GaoYuehua,WangXicheng.ASequentialOptimizationMethodwithMulti-pointSamplingCriterionBasedonKrigingSurrogateModel[J].EngineeringMechanics, 2012,29(4):90-95.

[12]于开平, 刘荣贺.多族群粒子群优化算法飞行器结构模型修正[J].振动与冲击, 2013,32(17):79-83.

YuKaiping,LiuRonghe.ModelUpdatingofaSpacecraftStructureBasedonMRPSO[J].JournalofVibrationandShock, 2013,32(17):79-83.

(编辑袁兴玲)

A New Structural Damage Identification Method Based on Kriging Surrogate Model

Guo JunlongMa LiyuanLi YongjunWang Tianhui

Ordnance Engineering College,Shijiazhuang,050003

A new damage identification method was proposed based on Kriging surrogate model. The initial samples were used to construct the initial Kriging surrogate model to represent the relationship between the dynamic response and the structural damage parameters instead of that between the dynamic response and the structural physics parameters. Reducing the finite element mesh generation and the finite element calculation during the damage identification effectively, the efficiency of damage identification was improved. Updating the Kriging surrogate model by sampling criterion, making sure the Kriging surrogate model might exactly describe the relationship between the dynamic response and the structural damage parameters. A numerical example of a tube and grider structure was given to prove the effectiveness of the method. Finally, the method was used in damage identification of a missile launch platform model. The results show that the method is effective.

damage identification; Kriging surrogate model; large and complex structure; severity identification

2015-05-13

军队科研项目([2012]80)

TU311

10.3969/j.issn.1004-132X.2016.09.011

郭俊龙，男，1990年生。军械工程学院导弹工程系硕士研究生。主要研究方向为装备状态监测与故障预测。马立元，男，1962年生。军械工程学院导弹工程系教授、博士研究生导师。李永军，男，1972年生。军械工程学院导弹工程系副教授。王天辉，男，1986年生。军械工程学院导弹工程系博士研究生。