基于形态滤波和Laplace小波的轴承故障诊断

臧怀刚　刘子豪　李玉奎

燕山大学工业计算机控制工程河北省重点实验室，秦皇岛，066004



基于形态滤波和Laplace小波的轴承故障诊断

臧怀刚刘子豪李玉奎

燕山大学工业计算机控制工程河北省重点实验室，秦皇岛，066004

针对强噪声背景下，轴承故障冲击响应的提取易被周围噪声干扰的问题，提出了一种基于数学形态学滤波和Laplace小波的包络谱分析方法。首先通过形态学滤波来滤除信号中的复杂噪声，增强信号的冲击特征，然后采用Laplace小波相关滤波法提取信号的冲击响应，最后对提取的冲击相关系数进行包络谱分析，即可诊断出故障。该方法结合了数学形态滤波和Laplace小波两者的优点，可以准确地捕捉到强噪声下的故障脉冲。将该方法应用于轴承内圈、外圈的故障诊断，与传统包络谱分析方法的对比结果很好地验证了所提方法的有效性。

形态滤波；Laplace小波；相关滤波；包络分析；故障诊断

0　引言

滚动轴承是各种旋转机械中最关键的零件之一，当其出现故障，将会产生周期性的脉冲冲击。若能有效地提取故障引起的脉冲冲击，便可以诊断出故障存在的部位[1-2]。然而工业现场环境复杂，故障特征信息往往被噪声所淹没，同时轴承振动信号具有非线性、非平稳的特征，所以常规的故障诊断方法难以取得理想的效果[3]。

对于故障信号的处理，如何有效地将故障脉冲信息从源数据中分离出来是首要问题。而信号分离的重点则是应用与信号波形最匹配的基函数对信号进行分解[4]，Laplace小波在满足小波的基本条件的同时，还具备与脉冲响应信号类似的单边衰减性质[5]，是故障诊断的理想工具。然而随着干扰噪声的增强，单纯的Laplace小波识别的准确率大大下降。数学形态滤波[6]是一种基于数学形态学变换的非线性滤波方法，近年来的研究结果表明，它可以有效地抑制噪声和其他干扰，是一种信号预处理的有效方法[7-8]。

本文系统地研究了Laplace小波的各种特性，着重对其单边衰减特性进行了分析。在此基础上，结合数学形态滤波，提出了一种基于数学形态滤波和Laplace小波的滚动轴承故障诊断方法。

1　数学形态滤波基本原理

形态滤波是一种基于数学形态学的非线性滤波器，其基本原理为设计一个称作结构元素的“探针”，通过探针在信号中的移动来提取有用的信息进行结构分析[9]，达到消除噪声并提取信号结构特征的目的。

1.1形态学变换

在形态学变换中，腐蚀(erosion)和膨胀(dilation)是两个基本运算，以此为基础可推导出其他常用的形态运算，如开运算、闭运算等。形态变换可以分为二值形态变换和灰度值形态变换[10-11]，由于轴承故障振动只涉及一维离散信号，故本文只对一维情况下的灰度值形态变换进行研究。基本形态运算的定义如下：

设信号f(n)为定义在F={0,1,…,N-1}上的离散函数，结构元素g(n)为G={0,1,…,M-1}上的离散函数，且N≫M，则f(n)关于g(n)的腐蚀和膨胀分别为

(f⊙g)(n)=min(f(n+m)-g(m))

(1)

(f⊕g)(n)=max(f(n-m)+g(m))

(2)

m=0,1,…,M-1

f(n)关于g(n)的开运算和闭运算分别为

(f∘g)(n)=(f⊙g⊕g)(n)

(3)

(f•g)(n)=(f⊕g⊙g)(n)

(4)

其中，符号⊙和⊕分别表示腐蚀和膨胀运算，符号∘和•分别表示形态开和形态闭运算。虽然这四种运算都能够提取信号的结构特征，但所采用的运算不同，取得的效果也不一样。这四种运算对信号中冲击成分的不同作用[12]见表1。

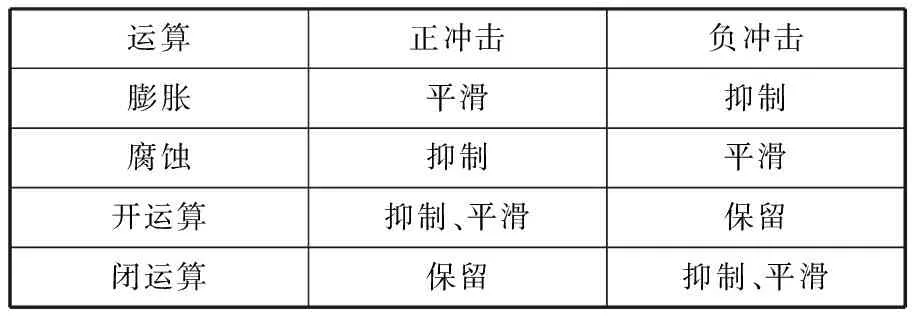
表1　形态学运算对冲击成分的作用

1.2滤波器的构建

从表1中可看出，膨胀、腐蚀、开运算和闭运算的滤波效果是不同的。为了能够同时去除信号中的正负两种噪声，通常采用开运算、闭运算的级联形式。Maragos等[13]提出通过不同顺序级联开运算、闭运算，得到形态开-闭滤波器和形态闭-开滤波器：

Foc(f(n))=(f∘g•g)(n)

(5)

Fco(f(n))=(f•g∘g)(n)

(6)

但是，由于开运算的收敛性导致开-闭滤波器的输出偏小，闭运算的扩张性导致闭-开滤波器的输出偏大，因而存在统计偏倚现象。因此，本文对故障信号的滤波处理采用以下组合滤波器：

(7)

1.3结构元素的选择

结构元素在形态滤波中的作用可以理解为一般信号处理中的滤波窗，其形状和长度是影响滤波的关键因素，常见的形状有扁平形、三角形、半圆形及正弦形等。据Nikolaou等[8]的分析结果，结构元素长度为脉冲周期长度的0.6～0.7倍时，去噪效果较好。考虑轴承故障信号的特点，为了最大程度地滤去噪声，同时保留信号中的脉冲响应成分，经反复试验验证，本文选取正弦形结构元素作为后续轴承故障信号去噪的结构元素。

2　Laplace小波相关滤波

2.1Laplace小波及其特性

Laplace小波是一种单边衰减的复指数小波[14]，其解析表达式为

ψ(ω,ζ,τ,t)=ψγ(t)=

(8)

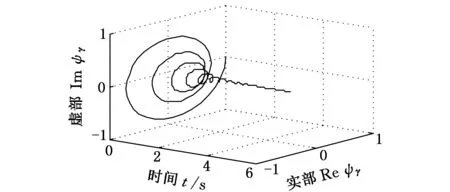
(a)Laplace小波

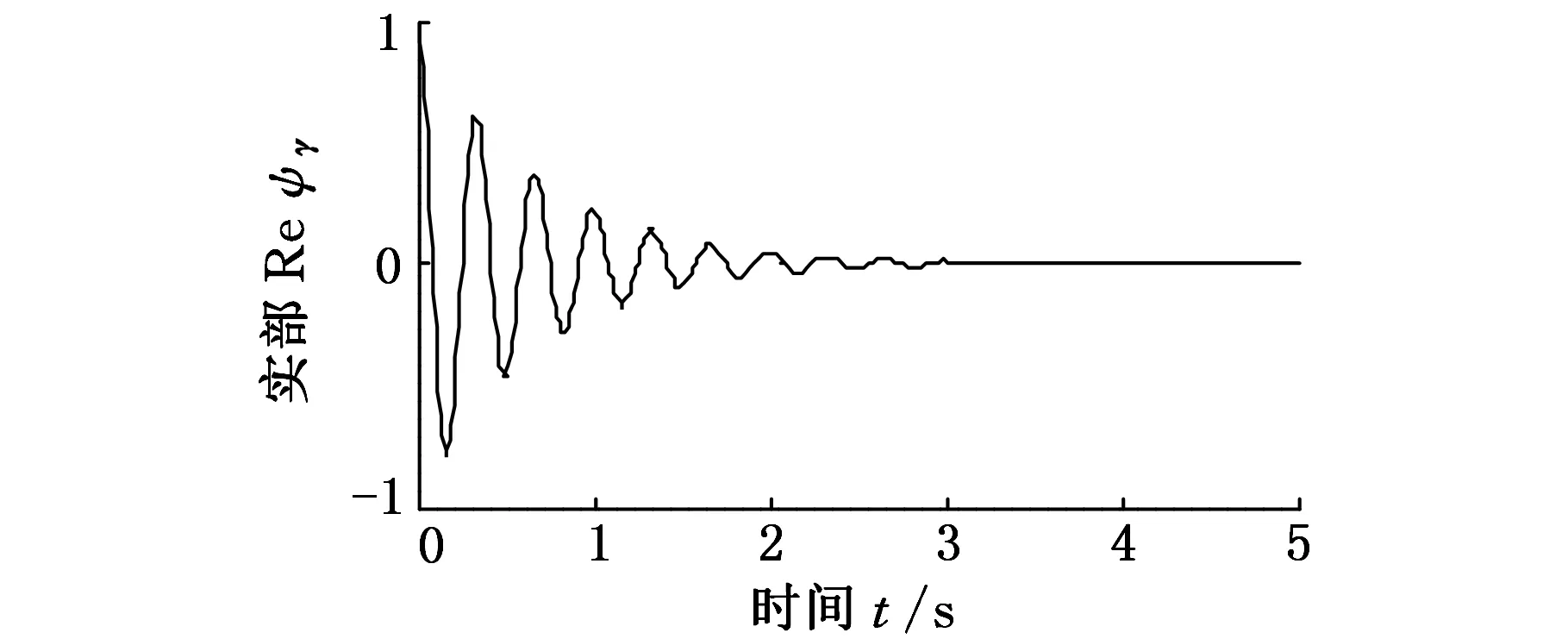
(b)Laplace小波实部图1　Laplace小波和轴承故障波形

2.2相关滤波

应用Laplace小波主要是为提取振动信号中的脉冲响应，不需要关心信号的其他成分。同时Laplace小波缺乏正交性，因而不能用基于正交展开的传统小波分解和重构的方法来应用Laplace小波[15-16]。基于这两点，本文提出了Laplace小波相关滤波法，搜寻信号中的单边衰减波形，实现被测对象中脉冲响应的提取。Laplace小波相关滤波法的实现方法如下。

一个参数矢量γ确定一个Laplace小波原子ψγ。对于两个有限长度的离散矢量x(t)和ψγ(t)，其内积可定义为

〈ψγ(t),x(t)〉=‖ψγ‖2‖x‖2cosθ

(9)

其中，‖ψγ‖2、‖x‖2表示矢量的模，θ为矢量的夹角。内积越大，则两者越相似。定义相关系数kγ来量化x(t)和ψγ(t)之间的相关程度，其表达式为

(10)

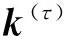
3　实际应用对比

处理轴承故障诊断问题最有效的方法之一就是包络谱分析，因为包络谱对周期性故障脉冲敏感。同时为了减少噪声干扰，提高诊断准确率，在包络分析之前，通常会利用各种滤波方法对信号作预处理。这就构成了最常用的一种故障诊断流程。

然而在实际工况下，背景噪声较强而且复杂，传统的包络谱分析对于某些故障情况，尤其是轴承早期微弱故障，并不能很准确地诊断出故障频率。按照本文方法，结合形态滤波和Laplace小波各自的优点，先通过形态滤波滤去原始信号中的噪声，再通过Laplace小波提取信号中反映轴承故障脉冲信息的相关系数，然后进行包络谱分析，可在一定程度上改进诊断结果。算法流程如图2所示。

图2　基于形态滤波和Laplace小波的轴承故障诊断算法流程图

下面针对某风力发电机驱动端轴承实际信号，分别就常规方法和本文改进方法的分析结果进行对比，进一步说明本文方法的有效性和可靠性。

轴承有关参数说明如下：风机型号为GamesaG58-850，轴承型号为SKF6326，内径为130mm、外径为280mm，转速为1611.116r/min，转频为26.852Hz，采样点数N=2048，采样频率fs为2500Hz。根据轴承手册和相关公式计算得出外圈、内圈故障频率分别为84.12Hz和130.70Hz。

3.1外圈频谱对比

首先对轴承外圈故障振动信号进行验证。图3a所示为轴承外圈故障振动信号的时域波形，不难看出，冲击响应信号完全被周围噪声淹没，无法看出明显的脉冲响应成分。图3b所示为形态滤波后得到的时域信号，经过形态滤波后，无关的噪声成分大大减少，同时突出了信号的结构特征。形态滤波完成后按照传统的包络分析流程，对滤波后的信号直接进行包络谱分析，结果如图4所示。

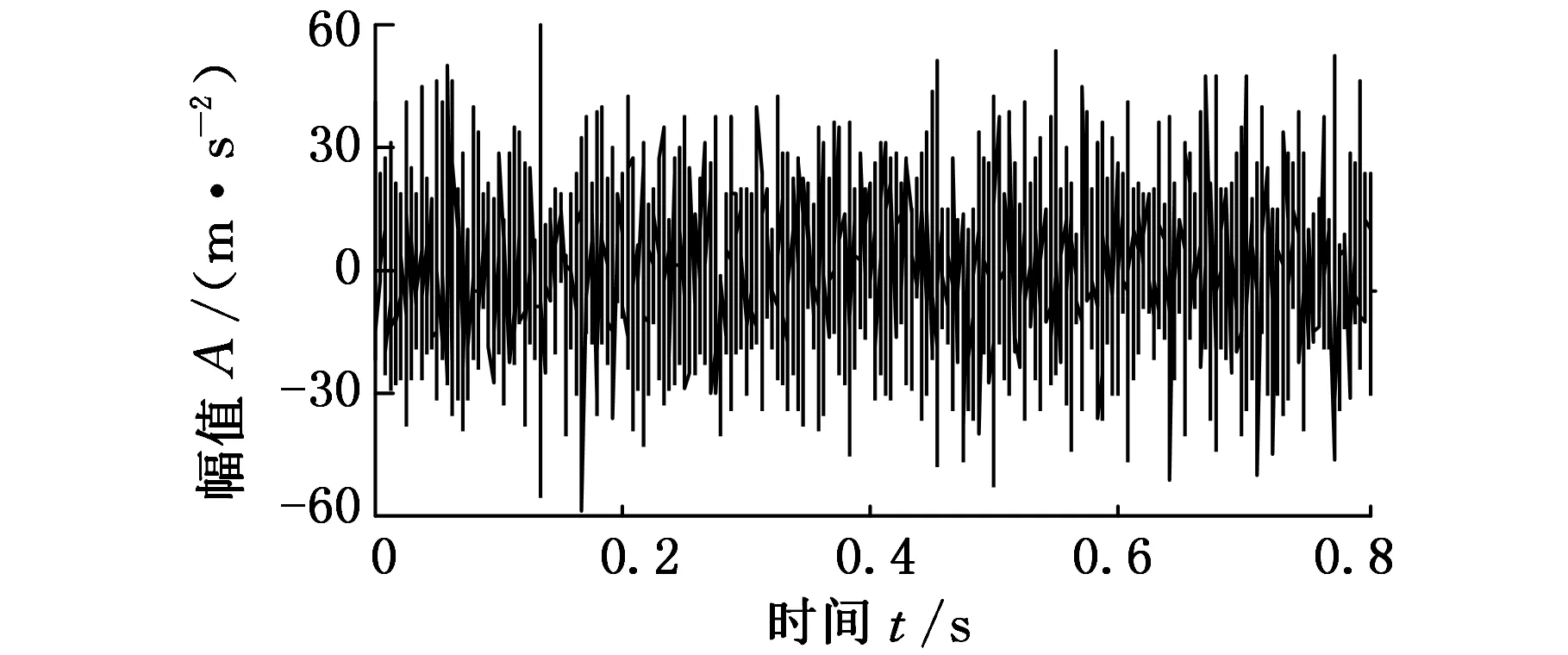
(a)原始信号

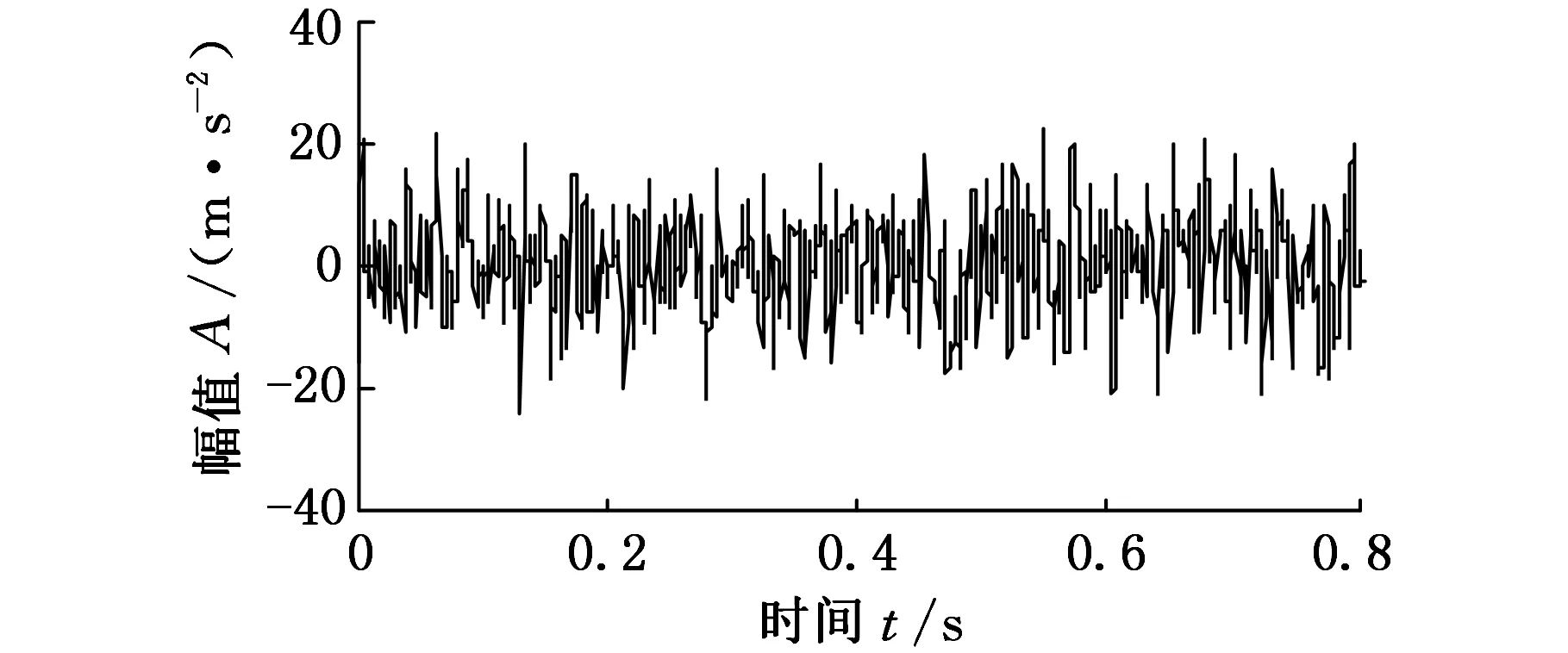
(b)形态滤波后信号图3　外圈故障振动波形

图4　外圈包络频谱

按本文改进方法进行分析，对形态滤波后信号进行Laplace小波相关滤波，提取的脉冲相关系数如图5所示。

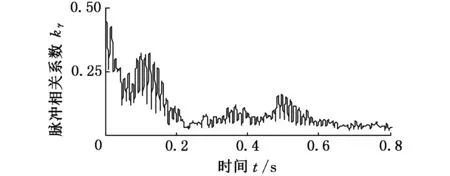
图5　滤波后的外圈相关系数

再对相关系数进行包络谱分析，结果如图6所示。频谱图上85.84Hz处存在明显的峰值，这与计算的外圈故障频率84.12Hz处基本相符，其二倍频169Hz和三倍频254Hz在频谱上也有明显的峰值，由此推断轴承外圈确实存在故障。因为相关系数曲线有一个总体衰减趋势，所以包络谱会存在一个8Hz的低频分量。

图6　外圈相关系数的局部包络谱

对比图4和图6可以看出，加入Laplace小波后，故障诊断结果更加准确，且没有边频等无关频率的影响，减少了误判率。

3.2内圈频谱对比

对内圈故障信号进行分析，图7a、图7b所示分别为轴承内环振动信号的原始信号和形态滤波后的信号。直接进行包络谱分析所得结果如图8所示。

由图8可看出，采用传统的包络谱分析方法虽然可以诊断出故障，但是频谱分析结果不清晰，存在大量的无关频率信息，这会对轴承故障的判断造成很大的影响。

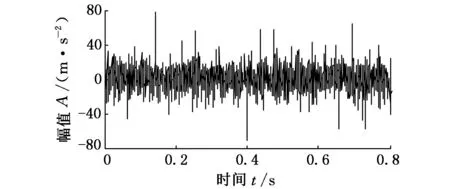
(a)原始信号

(b)形态滤波后信号图7　内圈故障振动波形

图8　内圈包络频谱

按本文方法提取相关系数并进行包络谱分析，结果分别如图9、图10所示，包络谱中可以明显看到132Hz的峰值与其二倍频264Hz，与计算的内圈故障频率130.7Hz基本相符。由此推断轴承内圈确实存在故障。

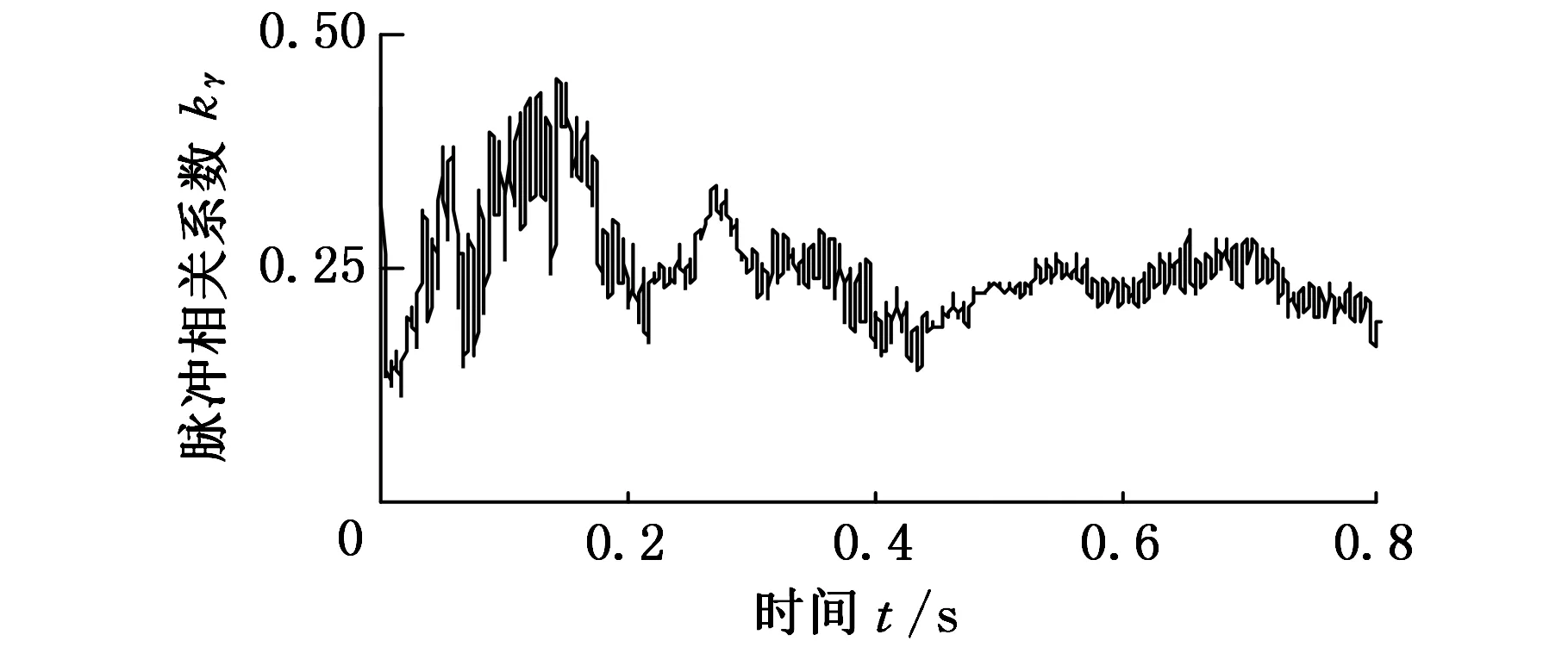
图9　滤波后的内圈相关系数

图10　内圈相关系数的局部包络谱

通过对Gamesa850风力发电机组驱动的轴承外圈、内圈故障振动信号的分析对比可以看出，采用数学形态滤波和Laplace小波相结合的方法对于故障频率的提取是很有效的。但应用该方法也存在缺点，因为Laplace小波需要进行大量卷积运算，所以比较耗时，不利于数据实时分析。此外，对于故障频率的诊断精度提升有限，总体来说仍需进行深入研究，使其在故障诊断方面得到更多的应用。

4　结论

(1)形态滤波应用于轴承故障诊断，结构元素的选择至关重要。通过分析，确定利用正弦形结构元素对信号进行匹配，抑制噪声和增强冲击特征的效果最好。

(2)Laplace小波具有单边衰减特性，应用Laplace小波作为基函数提取振动信号中的脉冲响应，效果更加显著。

(3)提出了一种基于数学形态滤波与Laplace小波相关滤波的包络谱分析方法，对轴承故障信号的分析结果表明：该方法比常用的传统包络谱分析方法精确、有效，具有实际应用价值。

(4)该方法计算量大，比较耗时，需进一步研究改进，提升该方法的诊断效率。

[1]张文斌，杨辰龙，周晓军.形态滤波方法在振动信号降噪中的应用[J].浙江大学学报(工学版)，2009，43(11)：2096-2099.

ZhangWenbin,YangChenglong,ZhouXiaojun.ApplicationofMorphologyFilteringMethodinVibrationSignalDenoising[J].JournalofZhejiangUniversity(EngineeringScience), 2009, 43(11):2096-2099.

[2]李季，潘孟春，唐莺，等.基于形态滤波和HHT的地磁分析与预处理[J].仪器仪表学报，2012，33(10)：2175-2180.

LiJi,PanMengchun,TangYing,etal.AnalysisandPreprocessingofGeomagneticSignalsBasedonMorphologicalFilterandHilbert-HuangTransform[J].ChineseJournalofScientificInstrument,2012,33(10):2175-2180.

[3]沈路，杨富春，周晓军，等.基于改进EMD与形态滤波的齿轮故障特征提取[J].振动与冲击，2010，29(3)：154-157.

ShenLu,YangFuchun,ZhouXiaojun,etal.GearFaultFeatureExtractionBasedonImprovedEMDandMorphologicalFilter[J].JournalofVibrationandShock,2010,29(3): 154-157.[4]訾艳阳，李庆祥，何正嘉.Laplace小波相关滤波法与冲击响应提取[J].振动工程学报，2003，16(1)：67-70.ZiYanyang,LiQingxiang,HeZhengjia.ExtractionofImpulseResponseBasedonCorrelationFilteringMethodofLaplaceWavelet[J].JournalofVibrationEngineering,2003,16(1):67-70.

[5]李建，武新军，孙鹏飞.基于实Laplace小波的脉冲涡流检测系统特性分析[J].仪器仪表学报，2013，34(11) 2056-2512.

LiJian,WuXinjun,SunPengfei.CharacteristicAnalysisofPulsedEddyCurrentTestingSystemBasedonRealLaplaceWavelet[J].ChineseJournalofScientificInstrument, 2013, 34 (11): 2506-2512.

[6]崔屹.图像处理与分析：数学形态学方法及应用[M].北京：科学出版社，2000.

[7]沈路.数学形态学在机械故障诊断中的应用研究[D].杭州：浙江大学，2010.

[8]NikolaouNG,AntoniadisIA.ApplicationofMorphologicalOperatorsasEnvelopeExtractorsforImpulsive-typePeriodicSignals[J].MechanicalSystemsandSignalProcessing, 2003, 17(6):1147-1162.

[9]郝如江，卢文秀，褚福磊.形态滤波器用于滚动轴承故障信号的特征提取[J].中国机械工程，2009，20(2)：197-201.

HaoRujiang,LuWenxiu,ChuFulei.MorphologicalFiltersinFeatureExtractionforRollingBearingDefectSignals[J].ChinaMechanicalEngineering,2009,20(2):197-201.

[10]章立军，杨德斌，徐金梧，等.基于数学形态滤波的齿轮故障特征提取方法[J].机械工程学报，2007，43(2)：71-75.

ZhangLijun,YangDebin,XuJinwu,etal.ApproachtoExtranetGearFaultFeatureBasedonMathematicalMorphologicalFiltering[J].ChineseJournalofMechanicalEngineering,2007,43(2):71-75.

[11]HeWei,JiangZhinong,QinQiang.AJointAdaptiveWaveletFilterandMorphologicalSignalProcessingMethodforWeakMechanicalImpulseExtraction[J].JournalofMechanicalScienceandTechnology,2010,24(8):1709-1716.

[12]王书涛，张金敏，李圆圆,等.基于数学形态学和模糊聚类的旋转机械故障诊断[J].仪器仪表学报，2012，33(5)：1055-1061.

WangShutao,ZhangJinmin,LiYuanyuan,etal.RotatingMachineryFaultDiagnosisBasedonMathematicalMorphologyandFuzzyClustering[J].ChineseJournalofScientificInsstument,2012,33(5):1055-1061.

[13]MaragosP,SchaferRW.MorphologicalFilters.PartⅡ:TheirRelationtoMedian,Order-statistic,andStackFilters[J].IEEETransactionsonASSP,1987,35(8): 1170-1184.

[14]祁克玉，向家伟，訾艳阳，等.基于Laplace小波相关滤波的结构模态参数精确识别方法[J].机械工程学报，2007，43(9)：167-172.

QiKeyu,XiangJiawei,ZiYanyang,etal.AnAccurateIdentificationMethodforStructuralModalParametersBasedonLaplaceWavelet[J].ChineseJournalofMechanicalEngineering,2007,43(9):167-172.

[15]吴俊伟.Laplace小波在机车轴承故障诊断中的应用研究[D].北京：北京交通大学，2009.

[16]江天，周培钰.经验模态分解Laplace小波在机车柴油机齿轮系故障诊断中的应用[J].机械工程学报，2011，47(7)：109-115.

JiangTian,ZhouPeiyu.FaultDiagnosisforGearTrainofLocomotiveDieselEngineBasedonEmpiricalModeDecompositionandLaplaceWavelet[J].JournalofMechanicalEngineering,2011,47(7):109-115.

(编辑陈勇)

Fault Diagnosis of Bearings Based on Morphological Filter and Laplace Wavelet

Zang HuaigangLiu ZihaoLi Yukui

Key Laboratory of Industrial Computer Control Engineering of Hebei Province，Yanshan University，Qinhuangdao，Hebei，066004

Under stronger noise background，the extraction of the impulse responses appearing in fault vibration signals was usually affected by noise around. Aiming at this issue，an envelopment analysis method was proposed to diagnose localized defects in bearings based on the mathematical morphological filtering and Laplace wavelet. Firstly，to filter the complex noises in the signals with morphological filter and to enhance the impact features of signals, then，the impulse responses were extracted by Laplace wavelet correlation filtering method. At last，the envelope spectrum analysis was carried out on the correlation coefficient of impulse responses. The advantages of morphological filter and Laplace wavelet were combined, which might accurately capture the fault pulses under strong noises. This method was applied to bearings fault diagnosis of the inner rings and outer rings. It is nice to verify the effectiveness of the proposed method by the results of the fault detection comparing with the traditional envelope spectrum analysis.

morphological filter; Laplace wavelet; correlation filtering; envelopment analysis; fault diagnosis

2015-06-16

TH133.33；TH165.3

10.3969/j.issn.1004-132X.2016.09.010

臧怀刚，男，1960年生。燕山大学电气工程学院副教授。主要研究方向为信号处理、超声波智能仪器仪表、实用型通信技术等。刘子豪，男，1988年生。燕山大学电气工程学院硕士研究生。李玉奎，男，1989年生。燕山大学电气工程学院硕士研究生。