基于FSWT细化时频谱SVD降噪的冲击特征分离方法

何志坚　周志雄

1.湖南大学，长沙，410082　　2.湖南信息职业技术学院，长沙，410200



基于FSWT细化时频谱SVD降噪的冲击特征分离方法

何志坚1,2周志雄1

1.湖南大学，长沙，4100822.湖南信息职业技术学院，长沙，410200

为有效提取滚动轴承故障振动信号的故障冲击特征，提出了基于FSWT细化时频谱SVD降噪的冲击特征分离提取方法。首先对原始信号进行频率切片小波变换得到全频带下的时频分布，然后根据时频谱能量分布特点选择出感兴趣的时频区域，再以较高的时频分辨率对感兴趣的时频区域进行细化分析得到细化的时频谱，从而分割出含有故障特征时频区域。为克服噪声对细化时频谱精度的影响，FSWT细化分析过程融入SVD降噪，通过对FSWT细化时频谱系数矩阵进行奇异值差分谱阈值降噪，使得FSWT细化时频谱的冲击特征更加明显，最后通对降噪后的细化时频谱进行FSWT逆变换重构，分离出故障冲击信号。仿真分析和故障诊断实例表明，基于FSWT细化时频谱SVD降噪的冲击特征分离提取方法能够成功从低信噪比信号中提取出周期性的冲击特征，有效地实现对滚动轴承各种故障的诊断。

频率切片小波变换；奇异值分解；滚动轴承；故障诊断

0　引言

滚动轴承是旋转机械系统的重要支撑元件，同时也是此类系统的主要故障来源。如何利用有效的故障诊断方法及时诊断出滚动轴承的各类故障，对于保障生产安全和减少经济损失具有重要意义[1]。

滚动轴承的各组成元件出现局部损伤故障时，故障点伴随滚动轴承的运行会与工作表面发生周期性的撞击，使得滚动轴承故障振动信号表现出显著的冲击性特征。理论上故障特征冲击频率即故障点被撞击的频率[2]。由于旋转机械系统结构设备的复杂性和工作环境的多样性，实际采集的滚动轴承故障振动信号为典型的非线性、非平稳信号。加之现场设备振源丰富以及大量噪声和干扰成分的影响，滚动轴承故障振动信号的冲击特征极易淹没在噪声和背景信号中，若能从复杂的信号成分中成功地分离冲击特征信号，则可有效地对滚动轴承的各种故障做出诊断[3]。

共振解调法是目前广泛应用的滚动轴承故障诊断方法，其核心思想是通过带通滤波获得处在共振频带的冲击性较强的振动信号，但如何自适应地确定带通滤波的带宽及中心频率一直是共振解调技术的难点[4]。为从滚动轴承故障振动信号中分离出故障特征信号，经验模态分解、集合经验模态分解、局部均值分解、本征时间尺度模态分解等自适应信号分解方法相继被应用到滚动轴承故障诊断中，并取得了较好的分析效果[5-8]。但由于信号分解方法自身的一些问题，分解出的信号仍受到一定的干扰。此外，时频分析方法也是处理滚动轴承故障振动信号的常用分析工具。典型的时频分析方法有短时傅里叶变换(STFT)、Wigner分布、连续小波变换(CWT)等[9-11]。

频率切片小波变换是在吸纳STFT和CWT所有优点基础之上提出的一种新的自适应时频分析方法。该方法的时频分辨率可控，可灵活地在时频空间进行区域分割和特定频率区间的信号重构[12]。由于FSWT的这些优良特性使之在机械故障诊断领域的研究逐渐兴起[13-14]。为有效提取滚动轴承故障特征信号的时频特征，同时从滚动轴承复杂的振动信号成分中分离出故障特征信号，本文将FSWT融合SVD，提出了一种基于FSWT细化时频谱SVD降噪的冲击特征分离提取方法。该方法首先利用FSWT全频带时频谱分析粗略估计滚动轴承的共振频带，然后通过对此频带信号进行细化分析，分离出故障特征信号的时频特征。为抑制噪声等干扰成分的影响，FSWT细化分析过程中融入SVD降噪，将FSWT细化分析时频谱系数矩阵进行SVD降噪突出细化时频谱的冲击特性，最后对降噪细化时频谱进行FSWT逆变换重构，分离出故障冲击信号。

1　FSWT基本原理

1.1FSWT算法

(1)

根据Parseval方程，可将式(1)转换到时域：

(2)

1.2FSWT尺度因子的选择

为不失分析的一般性，令λ=1，根据Morlet小波变换原理，σ∝ω，故设尺度因子σ=ω/k,k>0，则

(3)

其中，k与ω、u无关，用来调节FSWT的频率或时间的灵敏度，称作时频分辨率系数。同时式(2)可变为

(4)

由Heisenberg不确定性原理可知，无法同时在时域和频域得到高的分辨率，故频率切片小波变换中采用折中方案估计σ和ω，引入两个系数评价被分析信号，一是频率分辨比率η：

η=Δω/ω

(5)

(6)

即

(7)

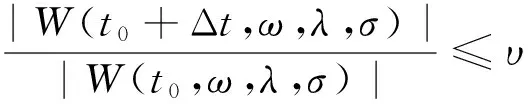
(8)

即

(9)

μ=ΔωΔt

1.3FSWT逆变换及细化时频谱

FSWT时频分析结果是冗余的，理论上其逆变换可采取不同的形式，其中一种最简单有效的逆变换形式为

(10)

式(10)表明，FSWT的逆变换与频率切片函数p(t)或p(ω)以及σ无关，逆变换可以直接用快速傅立叶变换求得[15]。

若信号f(t)的FSWT变换为W(t,ω,σ)，则在时频区域(t1,t2,ω1,ω2)的信号分量为

(11)

显然，可在f(t)的FSWT时频区间内选择任意的时频区域(t1,t2,ω1,ω2)即时频切片，同时可自由地在时频空间上提取所需的信号分量。实际故障诊断中可先对信号进行FSWT获得全频带的时频分布，然后观察时频分布的能量分布特点，选取感兴趣的时频切片进行细化分析，得到FSWT细化时频谱，并利用FSWT逆变换获取细化时频谱对应的信号分量。

2　SVD降噪

SVD降噪的本质是利用正交化理论消除信号的噪声成分[16]。设A为m×n型的实数矩阵，秩为r(r≤n)，则必存在m×m型的正交阵U和n×n型的正交阵V使得

A=UDVT

(12)

其中，D为m×n型的对角矩阵，D的主对角线元素(σ1,σ2,…,σr,0,…,0)为A的奇异值矢量。而此矢量的前面r个非零奇异值元素σ1,σ2,…,σr主要反映信号的有用成分和噪声成分的能量集中情况，且按照σ1≥σ2≥…≥σr的大小顺序排列。其中前i个元素将主要反映信号的有用成分，较小的奇异值σi+1,σi+2,…,σr主要反映噪声成分，将这一部分反映噪声成分的奇异值置零，就能够消除信号中的噪声成分，上述过程为SVD的降噪原理。影响SVD降噪效果的主要因素是信号中有用的奇异值个数的确定。为描述信号中有用成分和噪声成分的差异，实现奇异值个数的自动确定，文献[16]提出了奇异差分谱bj的概念，其定义为

bj=σj-σj+1j=1,2,…,r-1

(13)

奇异差分谱理论认为奇异值差分序列的最大突变点包含重要信息，选择最大峰值突变点对应的奇异值进行信号重构和实现理想的消噪效果，对于奇异值的选取具有一定的借鉴意义。同时实际应用中发现，仅选取最大峰值突变点对应的奇异值进行信号重构也容易使得一些弱冲击特征丢失。为了获得良好的降噪效果，同时尽可能保留信号的冲击特性，本文将奇异值差分谱中峰值群的最后一个峰值点序号对应的奇异值σi作为奇异值阈值，通过将小于此阈值的奇异值置零进行SVD降噪，其具体步骤如下：

(1)计算矩阵A的奇异值序列并得到奇异差分谱bj。

(2)观察奇异差分谱bj的分布，找出奇异差分谱峰值群最后一个峰值位置对应的奇异值σi。

(3)设定σi为奇异值选取阈值，将小于σi的奇异值置零。然后利用SVD降噪得到降噪矩阵B。

3　基于FSWT细化时频谱SVD降噪的冲击特征提取原理

滚动轴承原始故障振动信号x(t)为包含冲击特征信号、噪声及干扰频率成分的混合信号。为有效提取x(t)的故障冲击特征信号，本文提出了基于FSWT细化时频谱SVD降噪的冲击特征分离提取方法。具体步骤如下：

(1)对f(t)进行全频带FSWT分析，求取f(t)的时频分解系数W(t,ω,k)，得到f(t)在全频带下的时频谱。

(2)通过观察f(t)的全频带下时频谱的能量分布，选择感兴趣的频率切片区间[ω1,ω2]进行FSWT细化分析得到细化时频分布W(t,[ω1,ω2],k)，分割出含有故障特征时频区域。

(3)将细化时频谱W(t,[ω1,ω2],k)的系数矩阵作为矩阵A，进行SVD降噪突出细化时频分布的冲击特征，然后进行FSWT逆变换，分离出故障冲击特征信号。

4　仿真验证

为验证基于FSWT细化时频谱SVD降噪的冲击特征分离提取方法的有效性，利用文献[17]中的滚动轴承故障模型模拟滚动轴承外圈故障信号进行仿真验证。具体方法如下：

(14)

图1a所示为外圈故障冲击模拟信号s(t)的时域波形。图1b所示为x(t)的时域波形。可以看出由于噪声影响，滚动轴承的故障冲击特征不易被识别。

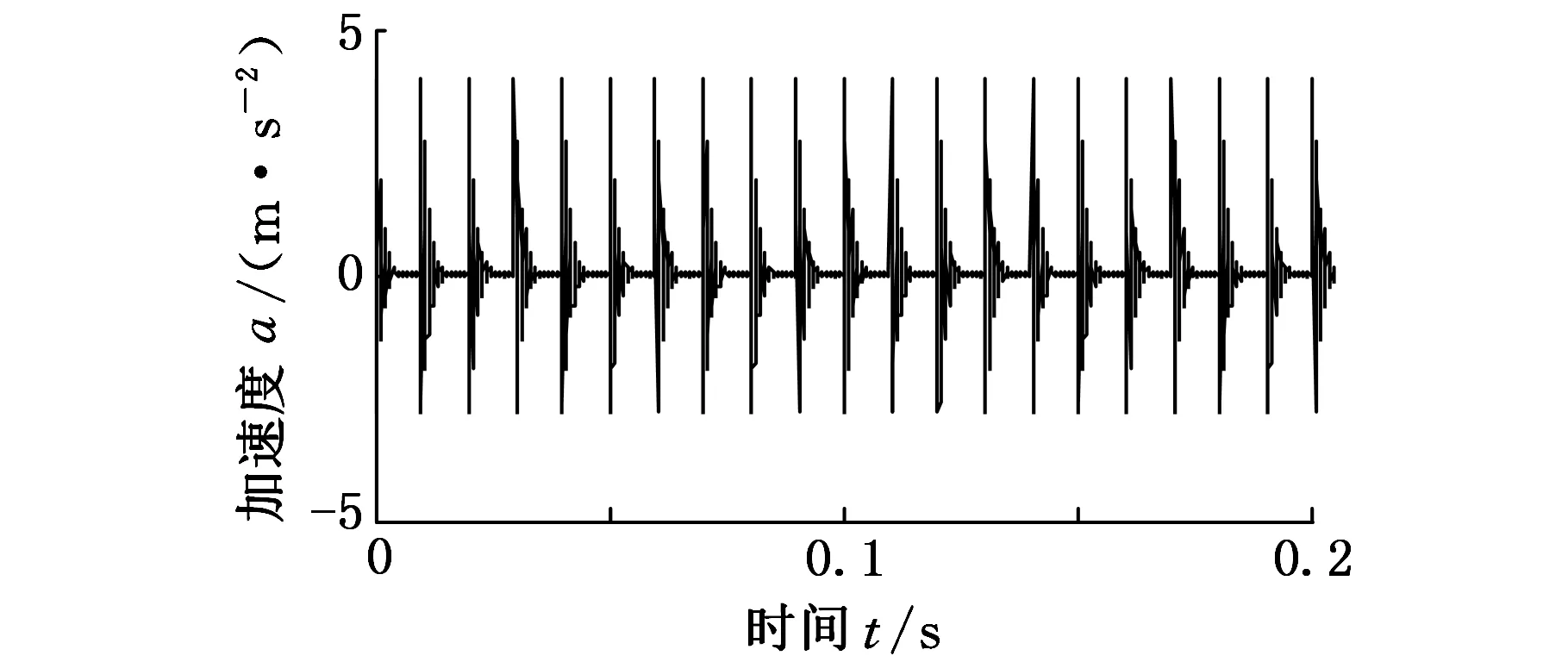
(a) s(t)的时域波形

(b) x(t)的时域波形图1　滚动轴承故障仿真信号

图2所示为采用频率切片函数p(ω)=e-0.5ω2对x(t)进行FSWT得到的全频带时频谱，其中η=0.08。从图2中可以看出颜色较深的能量集中频带中心频率为2000Hz。以2000Hz为中心频率，对[1000,3000]Hz的频带进行FSWT细化分析得到细化时频谱，见图3。细化时频谱的时频特征体现出一定的冲击性，但受困于背景噪声影响，造成冲击的具体时间间隔不易识别。对细化时频系数矩阵进行SVD降噪，图4所示为细化时频系数矩阵的奇异值差分谱。选择差分谱峰值群中最后一个峰值点的序号20作为奇异值谱阈值，FSWT细化时频谱SVD降噪结果如图5所示，图5中体现出明显的冲击特征，且沿时间轴的冲击间隔为0.01s，与滚动轴承的故障冲击周期一致。

图2　x(t)的FSWT全频带时频谱

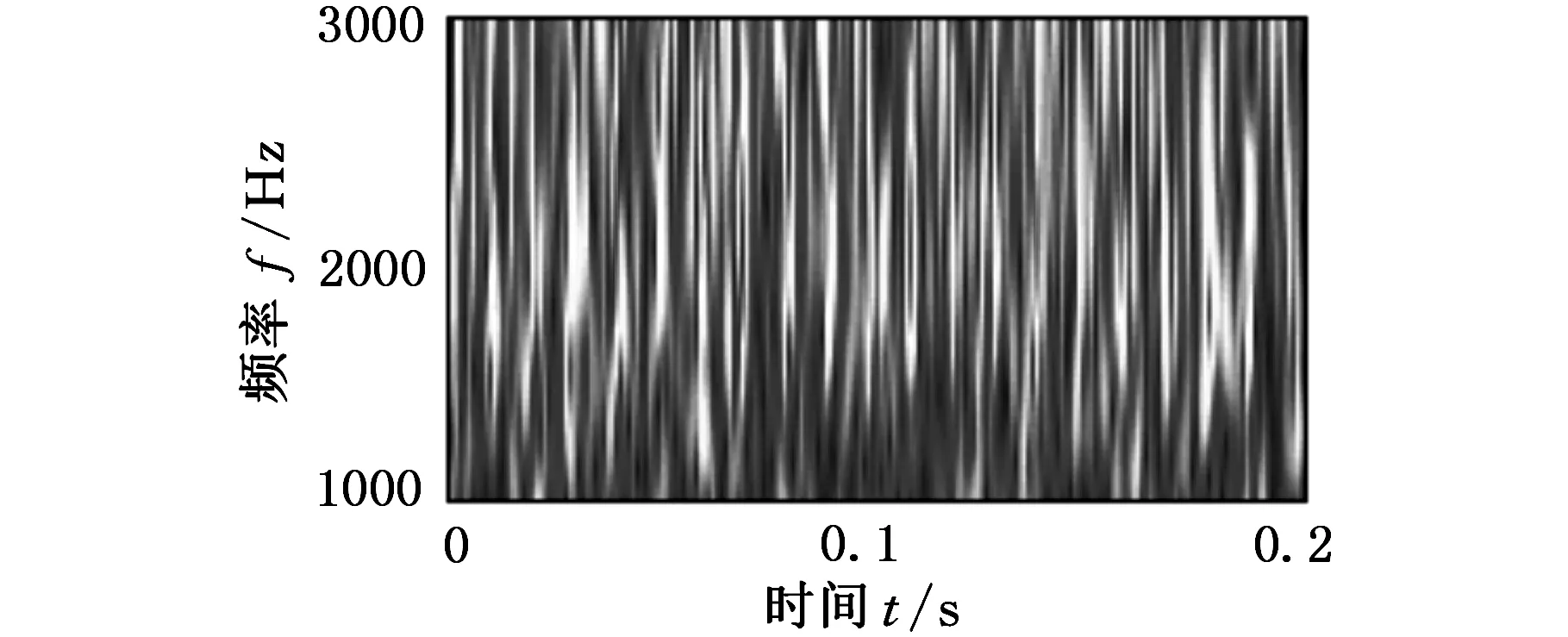
图3　x(t)的FSWT细化时频谱

图4　x(t)的FSWT细化时频谱系数矩阵奇异值差分谱

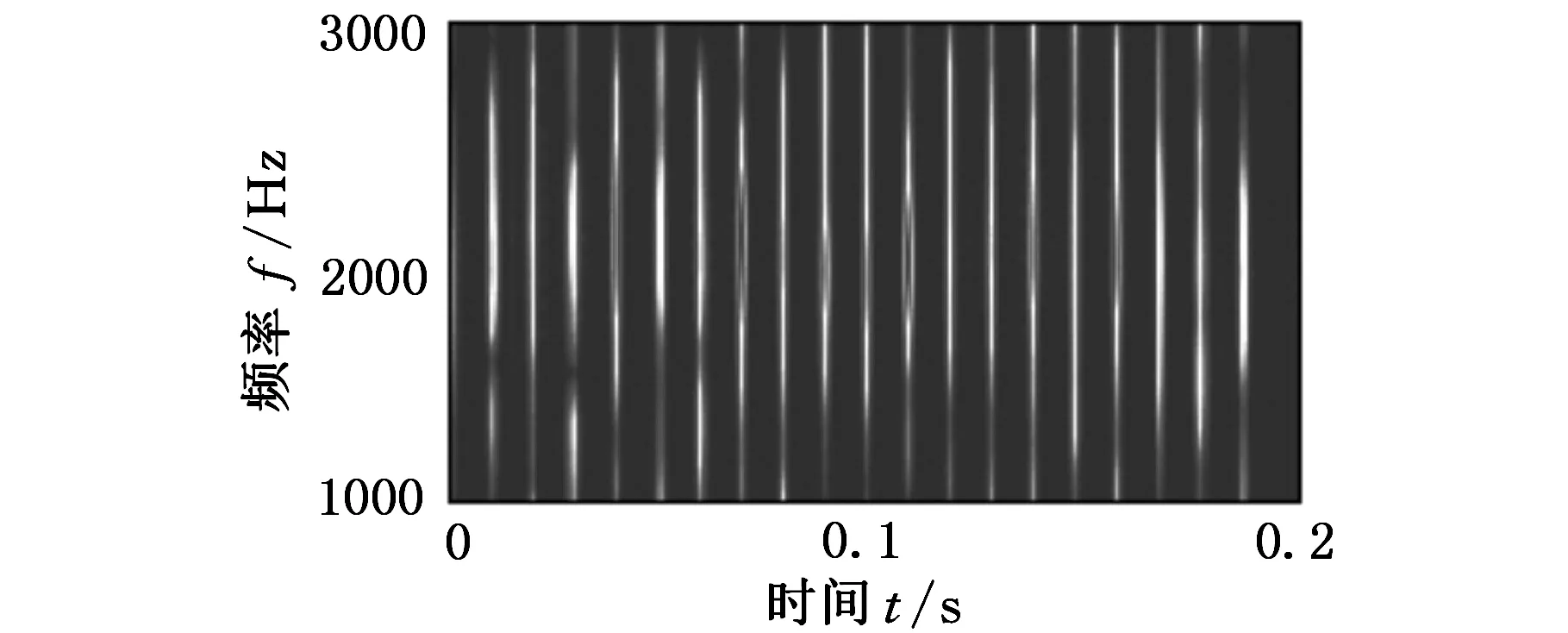
图5　x(t)的FSWT细化时频谱SVD降噪结果

选取SVD降噪的细化时频谱[1000,3000]Hz的频带并用式(11)对此频带的特征信号进行提取，结果如图6所示。虽然提取的冲击特征信号相对于原始冲击信号存在一定程度的变形和失真，但两者冲击特征重复频率表现一致，将故障诊断过程中最为重要的信息提取出来，同时有效地抑制了噪声。

图6　本文方法分离出的冲击特征信号

为充分体现该方法的优越性，同小波-SVD冲击特征提取方法进行了对比分析。小波基函数选用文献[18]中的Morlet小波。图7所示为信号x(t)的Morlet小波系数，由于存在噪声干扰，图7中显示的冲击特征并不明显。图8所示为对Morlet小波系数矩阵SVD降噪的奇异值差分谱，可看出其峰值特征与FSWT细化时频谱系数矩阵奇异值差分谱相比并不明显，难以通过本文方法确定阈值σi，在此效仿文献[18]选择小波系数前3个奇异值进行SVD降噪，结果如图9所示。降噪后的小波系数时频冲击特征得到增强，但冲击特性不如图5所示的本文方法的结果明显。图10所示为信号x(t)的Morlet小波-SVD特征提取结果，提取的特征信号时域冲击特征得到了增强，噪声得到了一定的抑制，但冲击增强效果仍不如图6所示的本文方法的分析结果。

图7　x(t)的Morlet小波系数

图8　x(t)的Morlet小波系数矩阵奇异值差分谱

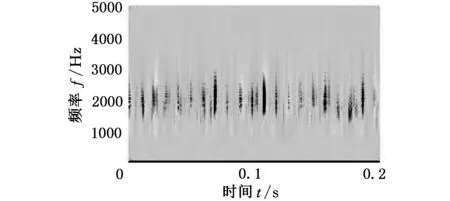
图9　保留前3个小波系数奇异值的SVD降噪结果

图10　x(t)的Morlet小波-SVD降噪结果

仿真分析结果表明，通过FSWT全频带时频谱找到滚动轴承的能量集中的故障特征频带，即与滚动轴承故障振动信号的共振频带相对应，对此频带进行细化时频谱SVD降噪可以有效地提取故障特征信号的时频冲击特征，将故障冲击特征信号从背景噪声中分离出来。并且该方法分析效果明显优于小波-SVD冲击特征提取方法的分析效果。与本文方法相比，小波-SVD冲击特征提取方法的小波基函数需要满足容许条件才可进行逆变换，且小波基函数一旦选定，小波系数就不会发生改变，缺乏广泛的自适应性。而频率切片小波变换可以调节参数改变时频谱的时频分辨率，以得到最佳的时频矩阵进行SVD降噪，自适应性强，且可以进行时频细化分析。

5　故障诊断实例

为进一步验证基于FSWT细化时频谱SVD降噪的冲击特征分离提取方法的有效性，采用美国凯斯西储大学电气工程实验室公开的轴承故障数据进行试验验证。试验中使用SKF6205-2RS型深沟球轴承，通过使用电火花在滚动轴承内圈上加工出0.1778mm的凹坑模拟单点微弱故障。选取的轴承内圈故障信号的采样频率为12kHz，分析点数为1024，转轴转速为1750r/min，轴承的各尺寸参数见表1，经理论计算可得到内圈故障频率(ballpassfrequencyoninnerrace，BPFI)约159.92Hz。

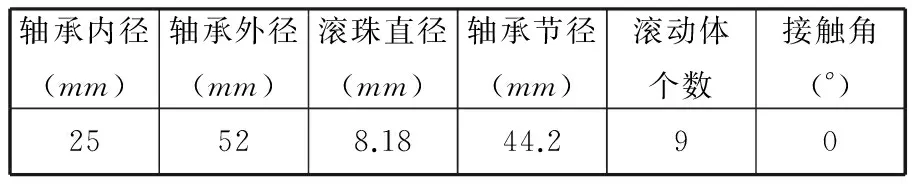
表1　轴承各尺寸参数

图11所示为内圈故障振动信号的时域波形，受噪声成分影响谱线较为杂乱，无法识别具体的冲击特征。对内圈故障振动信号采用函数p(ω)=e-0.5ω2进行FSWT(η=0.05)得到全频带时频谱，结果如图12所示。观察得出全频带时频谱中能量较大的频带的中心频率约为3500Hz。对[2500,4500]Hz的频带进行FSWT细化分析，图13所示为对应的细化时频谱。内圈故障信号的细化时频谱体现出一定的冲击特征，但背景干扰成分较多，造成冲击特征识别困难。为抑制噪声等干扰成分的影响，对细化时频谱系数矩阵进行SVD降噪分析，图14所示为细化时频谱系数奇异值差分谱，按照本文SVD降噪理论，选择差分谱峰值群中最后一个峰值点的序号13作为奇异值谱阈值，对细化时频谱进行奇异差分谱阈值降噪，结果如图15所示。降噪后的细化时频谱冲击特征更为明显，且完全抑制了噪声干扰。选取SVD降噪的细化时频谱[1000,3000]Hz的频带并采用式(11)对此频带的特征信号进行提取，结果如图16所示。分离出的冲击信号的冲击最小间隔Δt对应内圈故障振动信号的冲击周期，本文方法有效地抑制了噪声干扰，将滚动轴承的故障冲击成分提取出来。

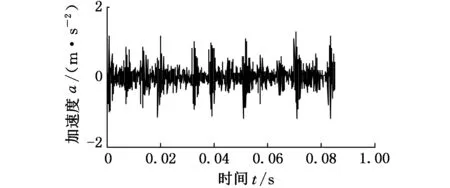
图11　内圈故障振动信号的时域波形

图12　内圈故障振动信号的FSWT全频带时频谱

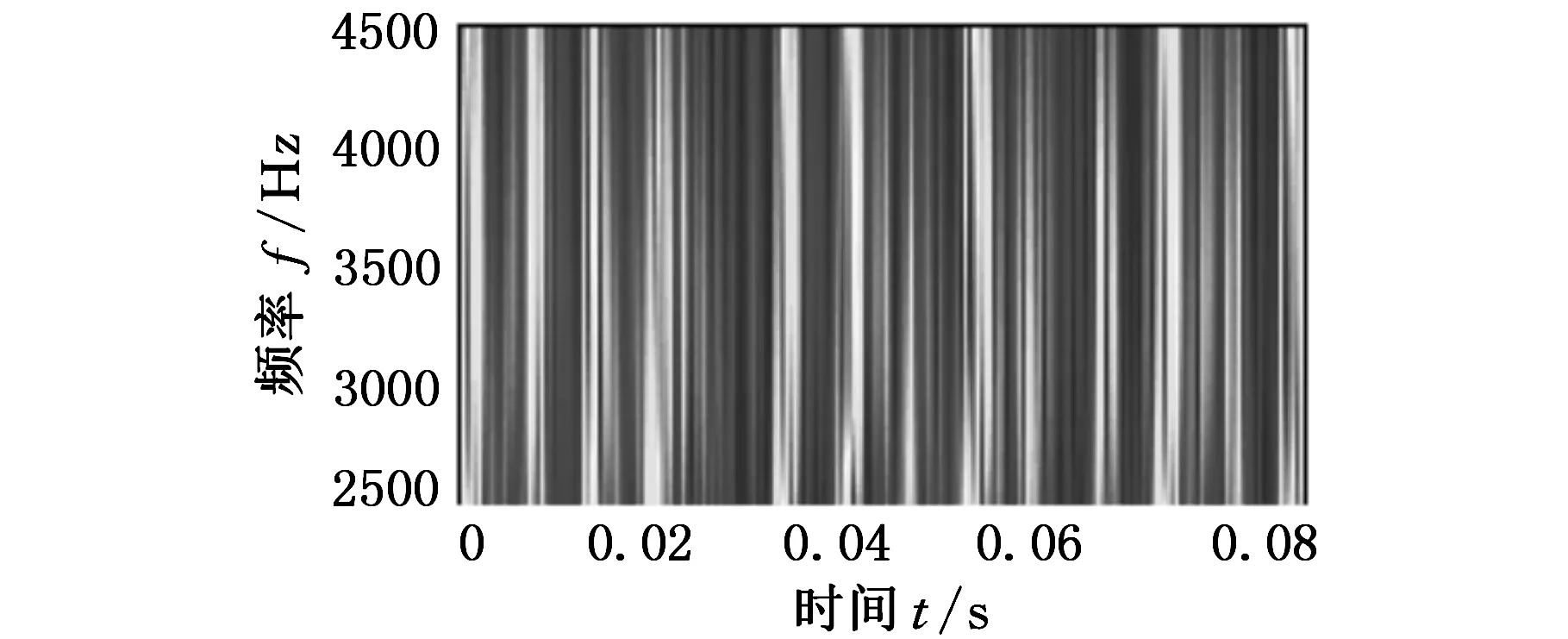
图13　内圈故障振动信号的细化时频谱

图14　细化时频谱系数的奇异值差分谱

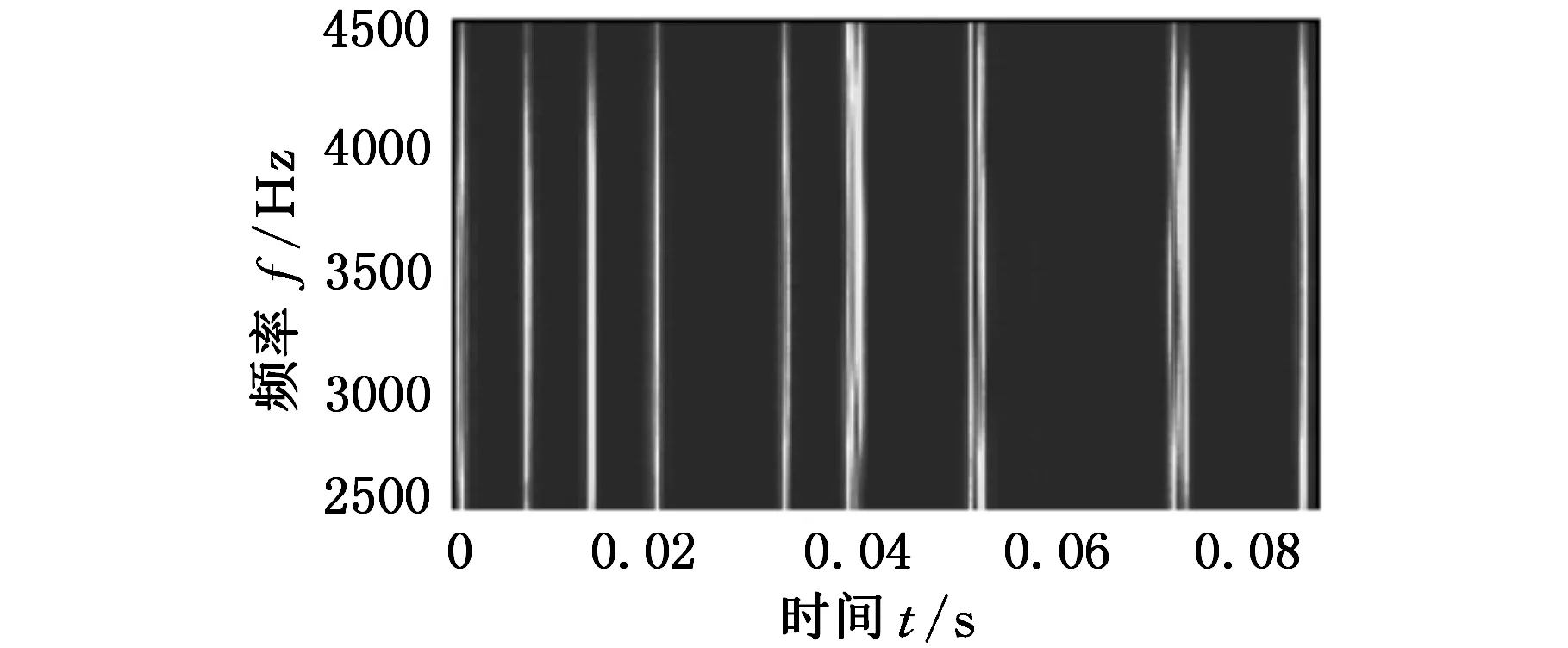
图15　细化时频谱的SVD降噪结果

6　结论

(1)FSWT通过引入频率切片函数可实现对原始信号的全频带时频分析及任意频带细化分析。通过观察全频带时频谱的能量分布可粗略估计信号的共振频带，对此频带进行时频区域细化分析可进一步得到细化时频谱，分离出隐含的时频故障特征，同时通过FSWT逆变换可分离出对应的故障冲击特征信号。

(2)将FSWT细化时频谱系数作为Hankel矩阵进行SVD降噪，可抑制噪声等干扰成分的影响，增强细化时频谱的冲击特性，同时使得分离出的故障特征信号的时域冲击特征增强。二者结合增强了FSWT的故障特征提取能力。

(3)基于FSWT细化时频谱SVD降噪的冲击特征分离提取方法可直观地、有效地提取滚动轴承故障特征信号的时频冲击及时域冲击特性，同时结合对应的滚动轴承故障特征频率可实现对滚动轴承各类故障的诊断。

[1]钟秉林, 黄仁. 机械故障诊断学[M]. 北京: 机械工业出版社, 2007.

[2]王天杨, 李建勇, 程卫东. 基于低次故障特征阶比系数的变转速滚动轴承等效转频估计算法[J]. 机械工程学报, 2015, 51(3): 121-128.

WangTianyang,LiJianyong,ChengWeidong.EquivalentRotationalFrequencyEstimationAlgorithmofFaultyRollingBearingunderVaryingRotationalSpeedBasedontheLowerFaultCharacteristicOrderCoefficient[J].ChineseJournalofMechanicalEngineering, 2015, 51(3): 121-128.

[3]王建国, 吴林峰, 秦绪华. 基于自相关分析和LMD的滚动轴承振动信号故障特征提取[J]. 中国机械工程, 2014, 35(2): 186-190.

WangJianguo,WuLinfeng,QinXuhua.RollingBearingVibrationSignalFaultFeatureExtractionMethodBasedonAutocorrelationAnalysisandLMD[J].ChinaMechanicalEngineering, 2014, 35(2): 186-190.

[4]王宏超, 陈进, 董广明, 等. 基于快速Kurtogram算法的共振解调方法在滚动轴承故障特征提取中的应用[J]. 振动与冲击, 2013, 32(1): 35-38.

WangHongchao,ChenJin,DongGuangming,etal.ApplicationofResonanceDemodulationinRollingBearingFaultFeatureExtractionBasedonFastComputationofKutrogram[J].JournalofVibrationandShock, 2013, 32(1): 35-38.

[5]LeiYaguo,LinJing,HeZhengjia,etal.AReviewonEmpiricalModeDecompositioninFaultDiagnosisofRotatingMachinery[J].MechanicalSystemsandSignalProcessing, 2013, 35(1):108-126.

[6]胡爱军, 马万里, 唐贵基. 基于集成经验模态分解和峭度准则的滚动轴承故障特征提取方法[J].中国电机工程学报, 2012, 32(11): 106-111.

HuAijun,MaWanli,TangGuiji.RollingBearingFaultFeatureExtractionMethodBasedonEnsembleEmpiricalModeDecompositionandKurtosisCriterion[J].ProceedingsoftheCSEE, 2012, 32(11): 106-111.

[7]ZhuangYunpeng,GaiQiang,ZhouYang.ApplicationofLocalMeanModeDecompositioninBearingFaultDiagnosis[J].InformationEngineeringandApplications, 2012, (15):323-330.

[8]AnXuli,JiangDongxiang,ChenJie,etal.ApplicationofIntrinsicTime-scaleModeDecompositionMethodtoWindTurbineBearing[J].JournalofVibrationandControl, 2012, 18 (2):240-245.

[9]Al-BadourF,SunarM,ChededL.VibrationAnalysisofRotatingMachineryUsingTime-frequencyAnalysisandWaveletTechniques[J].MechanicalSystemsandSignal, 2011, 25(6): 2083-2101.

[10]龚海建, 黄伟国, 赵凯, 等. 基于Wigner-Ville分布于小波融合的时频特征提取方法[J].振动与冲击, 2011, 30(2): 35-38.

GongHaijian,HuangWeiguo,ZhaoHai,etal.Time-frequencyFeatureMethodBasedonWinger-VilleDistributionandWaveletScalogram[J].JournalofVibrationandShock, 2011, 30(12): 35-38.

[11]程军圣, 于德介, 邓乾旺, 等. 连续小波变换在滚动轴承故障诊断中的应用[J]. 中国机械工程, 2003, 14(3): 2037-2040.

ChengJunsheng,YuDejie,DengQianwang,etal.RollingBearingFaultDiagnosisUsingContinuousWaveletTransform[J].ChinaMechanicalEngineering, 2003, 14(3): 2037-2040.

[12]YanZ,MiyamotoA,JiangZ,etal.AnOverallTheoreticalDescriptionofFrequencySliceWaveletTransform[J].MechanicalSystemsandSignalProcessing, 2010,24(2): 491-507.

[13]段晨东, 高强. 基于时频切片分析的故障诊断方法及应用[J].振动与冲击, 2011, 30(9): 1-5.

DuanChendong,GaoQiang.NovalFaultDiagnosisApproachUsingTime-frequencySliceAnalysisandItsApplication[J].JournalofVibrationandShock, 2011, 30(9): 1-5.

[14]钟先友, 赵春华, 陈宝家, 等. 基于形态自相关和时频切片分析的轴承故障诊断方法[J]. 振动与冲击, 2014, 33(4): 11-16.

ZhongXianyou,ZhaoChunhua,ChenBaojia,etal.BearingFaultDiagnosisMethodBasedonMorphologicalFiltering,Time-delayedAutocorrelationandTine-frequencySliceAnalysis[J].JournalofVibrationandShock, 2014, 33(4): 11-16.

[15]YanZ,MiyamotoA,JiangZ.FrequencySliceWaveletTransformforTransientVibrationResponseAnalysis[J].MechanicalSystemsandSignalProcessing, 2009, 23(5): 1474-1489.

[16]赵学智, 叶邦彦, 陈统坚. 奇异值差分谱理论及其在车床主轴箱故障诊断中的应用[J]. 机械工程学报, 2010, 46(1): 100-108.

ZhaoXuezhi,YeBangyan,ChenTongjian.DifferenceSpectrumTheoryofSingularValueandItsApplicationtotheFaultDiagnosisofHeadstockofLathe[J].ChineseJournalofMechanicalEngineering, 2010, 46(1): 100-108.

[17]HoD,RandallRB.OptimizationofBearingDiagnosticTechniqueUsingSimulatedandActualBearingFaultSignals[J].MechanicalSystemandSignalProcessing,2000,14(5):763-788.

[18]耿宇斌, 赵学智. 基于Morlet小波变换与SVD的故障特征提取[J]. 华南理工大学学报(自然科学版), 2014, 42(7): 55-61.

GengYubin,ZhaoXuezhi.FaultFeatureExtractionBasedonMorletWaveletTransformandSingularValueDecomposition[J].JournalofSouthChinaUniversityofTechnology(NaturalScienceEdition), 2014, 42(7): 55-61.

(编辑陈勇)

Impact Feature Separation Method Based on FSWT Zoom Time-frequency Spectrum De-noised by SVD

He Zhijian1,2Zhou Zhixiong1

1.Hunan University,Changsha，410082 2.Hunan College of Information,Changsha，410200

In order to extract the impact features of rolling bearings effectively,an impact feature separation method was proposed based on FSWT zoom time-frequency spectrum de-noised by SVD. Firstly, the original signals were analyzed by FSWT to get their whole time-frequency distributions. Then the interesting time-frequency region could be selected according to the time-frequency energy distribution characteristics, furthermore the fault characteristics region could be separated by a zoom analysis to the interested time-frequency region with higher resolutions. So as to inhibit the influences of the noise on the accuracy of zoom time-frequency distribution maps, FSWT zoom analysis was integrated with the SVD de-noising process, the FSWT zoom analysis time-frequency distribution matrix was de-noised by the SVD singular value difference spectrum threshold de-noising method to make the impact features outstanding. Finally, the fault impulse signals were separated by applying the FSWT inverse transform to the de-noised zoom analysis time-frequency spectrum. The simulated analysis and actual fault diagnosis example results demonstrate the impact feature separation method based on FSWT zoom time-frequency de-noised by SVD may extract the periodic impact features from low SNR signals and accomplish the fault diagnosis of rolling bearings.

frequency slice wavelet transform (FSWT); singular value decomposition(SVD); rolling bearing; fault diagnosis

2015-06-04

国家科技重大专项(2012ZX04003041)；国家自然科学基金资助项目(51475158)

TH13

10.3969/j.issn.1004-132X.2016.09.008

何志坚，男，1974年生。湖南大学机械与运载工程学院博士研究生，湖南信息职业技术学院高级工程师。主要研究方向为机床设备故障诊断与复杂刀具设计。周志雄，男，1953年生。湖南大学机械与运载工程学院教授、博士研究生导师。