基于贝叶斯网络的复杂系统动态故障树定量分析方法

房丙午,黄志球,李　勇,王　勇

(1.南京航空航天大学计算机科学与技术学院,江苏南京 210016;2.安徽财贸职业学院电子信息系,安徽合肥 230061)



基于贝叶斯网络的复杂系统动态故障树定量分析方法

房丙午1,2,黄志球1,李勇1,王勇1

(1.南京航空航天大学计算机科学与技术学院,江苏南京 210016;2.安徽财贸职业学院电子信息系,安徽合肥 230061)

动态故障树的贝叶斯网络分析方法存在局部组合爆炸和备件门节点失效时间仅能是指数分布的不足.首先,给出动态故障树转换为离散时间贝叶斯网络的方法,该方法使用一个确定性函数来替代条件概率表,避免了局部组合爆炸.然后,根据备件门的失效机理和对应的贝叶斯网络结构特征,解决了备件节点失效时间仅能是指数分布的限制.最后,提出一种基于动态故障树的贝叶斯网络精确推理算法,基于该算法给出了系统失效分布、组件重要度等概率计算.实验结果表明,该方法能有效地分析和评估安全攸关系统的概率特性.

动态故障树;贝叶斯网络;定量分析;安全攸关系统

1　引言

动态故障树(DFT)通过定义优先与门,备件门和功能依赖门等动态门来扩展故障树的建模能力,使其在具有时间相关性、功能相关性等复杂系统安全性分析领域获得广泛应用[1,2].DFT是半形式化模型,需要转换为数学模型进行分析[2],但是随着系统规模和复杂性的增长,DFT模型也越来越复杂,目前的分析方法存在状态空间爆炸和组件失效时间仅服从指数分布等缺点,难以适应大型复杂系统DFT分析需求.

DFT分析方法主要分为状态空间分析法[2～5],代数解析法[6～8],仿真方法[9,10]和贝叶斯网络分析法(BN)[11～19]四类.状态空间分析法存在状态空间爆炸和只能处理组件失效时间服从指数分布.代数解析法理论性强,无工具支撑,建模工作量大、易出错.仿真方法可以处理任意失效分布,但计算精度不高.BN分析法避免了全局状态空间爆炸,但存在条件概率表的参数组合爆炸和备件节点失效时间仅能是指数分布.针对上述不足,本文在离散时间BN(Discrete-Time BN,DTBN)分析法的基础上,提出针对大型复杂系统DFT分析方法:(1)给出一种DFT向DTBN转换方法.将非根节点CPD表示为父节点的一个确定性函数,避免条件概率表指数增长问题.(2)给出BN中备件节点CPD计算方法,克服了备件节点失效时间只能是指数分布的限制.(3)根据DFT转换的BN结构特征,提出一种基于DFT的BN推理算法.实验结果表明,本文提出的方法计算效率和精度优于DTBN方法,能有效地避免条件概率表指数增长并能分析任意失效分布,满足大型复杂系统DFT分析需求.

2　DFT向BN转换方法

DFT逻辑门包括与门(AND)、或门(OR)和K/M选举门,动态门包括顺序增强门(SequentialEnforcingGate,SEQ)、优先与门(PriorityAND,PAND)、备件门(SPare,SP)和功能依赖门(FunctionalDEPendencygate,FDEP)[2,3].K/M选举门可由与门和或门组合表示[4],SEQ可由备件门组合表示[11].本节给出AND、OR、PAND、SP和FDEP向BN转换.DFT门表示、建模场景和失效机理参见相关文献[2,3].

2.1DFT门的BN结构表示

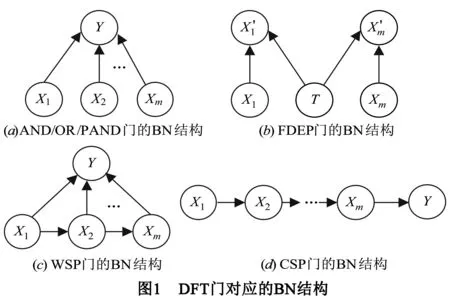
DFT门对应的BN结构如图1所示,其中X=(X1,X2,…,Xm)表示组件向量对应BN根节点集合,Y表示(子)系统,对应BN的中间节点或叶节点. Y的CPD表示DFT门的一种逻辑或时序关系,是父节点的一个确定性函数,如式(1)所示

(1)

其中,pay表示Y的父节点.

为了表达动态门时序关系将BN节点CPD按失效时间离散化[12].整个时间 [0,+∞)划分成n+1个子区间,其中,任务时间区间[0,T]被分成n个长度相等的子区间,每个子区间的长度为Δ=T/n,第n+1个子区间是(t,∞).节点的状态由子区间 (0,Δ],(Δ,2Δ],…,((n-1)Δ,nΔ],(nΔ,+∞)来表示.如果在任务时间T内,节点X在第i∈{1,2,…,n})个区间((i-1)Δ,iΔ]内发生失效,记为X=i.X=n+1表示X在T内未失效而是在[t,∞)内失效.在整个时间[0,+∞)上,节点必然处在某一状态.

2.2BN中子系统节点参数表示

AND/OR/PAND门对应的BN结构相同,如图1(a)所示,但Y的CPD是不同的.根据AND门失效机理,Y状态是所有组件状态值的最大值,Y的CPD由式(2)表示.根据OR门失效机理,Y状态是所有组件状态值的最小值,Y的CPD由式(3)表示.PAND门在AND门上增加组件失效时序约束,Y的CPD由式(4)表示.

(2)

(3)

P(Y=l|X)=

(4)

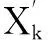
(5)

SP门包括温备件门(WSP),冷备件门(CSP)和热备件门(HSP).WSP和CSP门的BN结构如图1(c)和(d)所示,X1为主件,X2,…,Xm为备件,HSP门主件和备件同时处于工作状态,BN结构和节点的CPD和AND门等价[14].根据WSP门失效机理,Y的CPD和AND门Y的CPD相同由式(2)表示.CSP对应的BN中一旦Xm失效,Y立即失效,Y的CPD由式(6)表示.

(6)

2.3BN中备件节点CPD计算

在SP对应的BN中,备件节点失效行为受父节点的影响,目前的BN分析方法仅能处理节点失效时间服从指数分布[12～14],本节根据备件门失效机理和对应BN结构,将备件节点失效分布扩展为任意分布.

假设组件失效率为λ(t),作备件时,失效率由其工作状态决定,处于激活状态失效率为λ(t),处于备用状态失效率为αλ(t)(冷备件α=0,热备件α=1,温备件0<αλ(t)<1).Xk-1和Xk是SP对应BN中的两个组件,Xk-1是Xk父节点,失效时间分别为tk和tk-1.首先给出WSP对应BN备件节点的条件概率密度函数,分两种情况来讨论:

(1)tk≤tk-1,Xk在Xk-1之前或同时失效,也就是Xk在备用状态失效,Xk失效不受Xk-1影响,条件概率密度函数如式(7)所示.

=αfXk(tk)[1-FXk(tk)]α-1,tk≤tk-1

(7)

(2)tk>tk-1,Xk-1在Xk之前失效,由于Xk-1失效,使Xk进入工作状态,Xk失效受Xk-1影响且Xk和Xk-1都在激活状态失效,条件概率密度函数如式(8)所示.Xk的CPD分别由式(9)计算.

fXk|Xk-1(tk|tk-1)

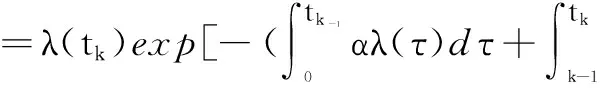
=fXk(tk)[1-FXk(tk-1)]α-1,tk>tk-1

(8)

P(Xk=i|Xk-1=j)=

(9)

对于CSP门,α=0,Xk不会在Xk-1之前失效,Xk的CPD由式(10)计算,

P(Xk=i|Xk-1=j)=

(10)

3　基于DFT的BN推理算法

DFT转换的BN是典型的层次结构,失效行为传播方式是自底向上的,利用该特征来优化通用BN推理算法,以提高分析效率.算法1通过BN中子系统节点来组织变量消元.基本操作是CPD相乘和求和操作.节点CPD是父节点的确定性函数,采用决策树存储CPD[20].在算法1中,Ф表示子系统的后验边缘分布,Ψ表示节点CPD,Xij和Yij分别表示第i层第j个组件和子系统,Z和C分别表示Yij拥有的下层子系统和组件集合,P表示Xij父节点的集合.

算法1效率分析,(1)时间复杂度用第10行函数来度量,该函数变量个数是|C|+|Z|+1,假设BN中子系统结点个数为m,组件个数为k(一般k远大于m),节点的状态数为n,那么算法1 时间复杂度为O(mn|C|+|Z|+1),而采用连接树推理算法[20]时间复杂度大于O((m+k)n|C|+|Z|+1).(2)存储空间方面,采用决策树存储CPD,存储空间由O(mnm)降低为O(mn)解决了局部存储空间爆炸问题(m为某一节点的父节点数).

4　实验分析

根据DFT到BN转换方法,图2给出了心脏辅助系统(Cardiac Assist System,CAS)DFT模型[12]等价的BN结构.BN采用SamIam分析工具,CTMC采用Galieo DFT分析工具,代数解析法(Algebraic Analysis,AA)采用MATLAB进行辅助计算.实验平台配置为CPU型号为Intel I5,主频为2.6 GHz,内存为4GB.本文提出的方法记为IDTBN,分别与DTBN、CTMC和AA进行比较.

4.1性能分析

假设CAS各组件的失效时间服从指数分布,WSP中α=0.5,各组件失效率如表1所示.

表1　CAS系统各组件的失效率

表2给出不同的离散时间粒度下IDTBN和DTBN的执行时间.从表2可以看出,随着n的增大,IDTBN时间性能明显优于DTBN,当n=30时计算时间相差两个数量级,IDTBN时间性能基本满足系统实时分析的需求.

表3给出n=3时,T从1h到10h,分别使用CTMC、IDTBN和DTBN计算的CAS失效概率.

IDTBN和DTBN计算结果相对CTMC的误差如图3(a)所示,DTBN最大相对误差为5.47‰,算术平均误差是2.29‰.标准误差是3.13‰;IDTBN最大相对误差为3.42‰,算术平均误差是1.39‰.标准误差是1.92‰,从计算结果可以看出,IDTBN计算精度要优于DTBN.

表2　IDTBN和DTBN方法的执行时间

表3　CTMCs 、IDTBN和DTBN方法计算的系统失效概率

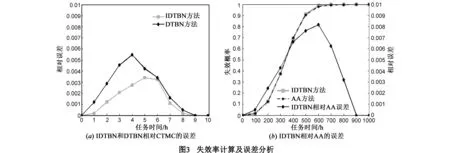
选取CPUs子系统验证IDTBN处理失效时间服从任意分布的有效性,假设组件失效时间服从威布尔分布,尺度参数a=500,形状参数b=3,T=1000h,n=3.图3(b)分别给出了IDTBN与AA计算的CPUs子系统失效概率和相对误差,其中最大相对误差为8.17‰,算术平均误差是3.08‰.标准误差是4.52‰.

4.2系统组件重要度及后验失效分布计算

在表1的参数设置下,n=3,T=10h,IDTBN和CTMC的组件Birnbaum重要度计算结果如表4所示.虽然结果存在一定的误差,但这并不影响组件重要度的定性.

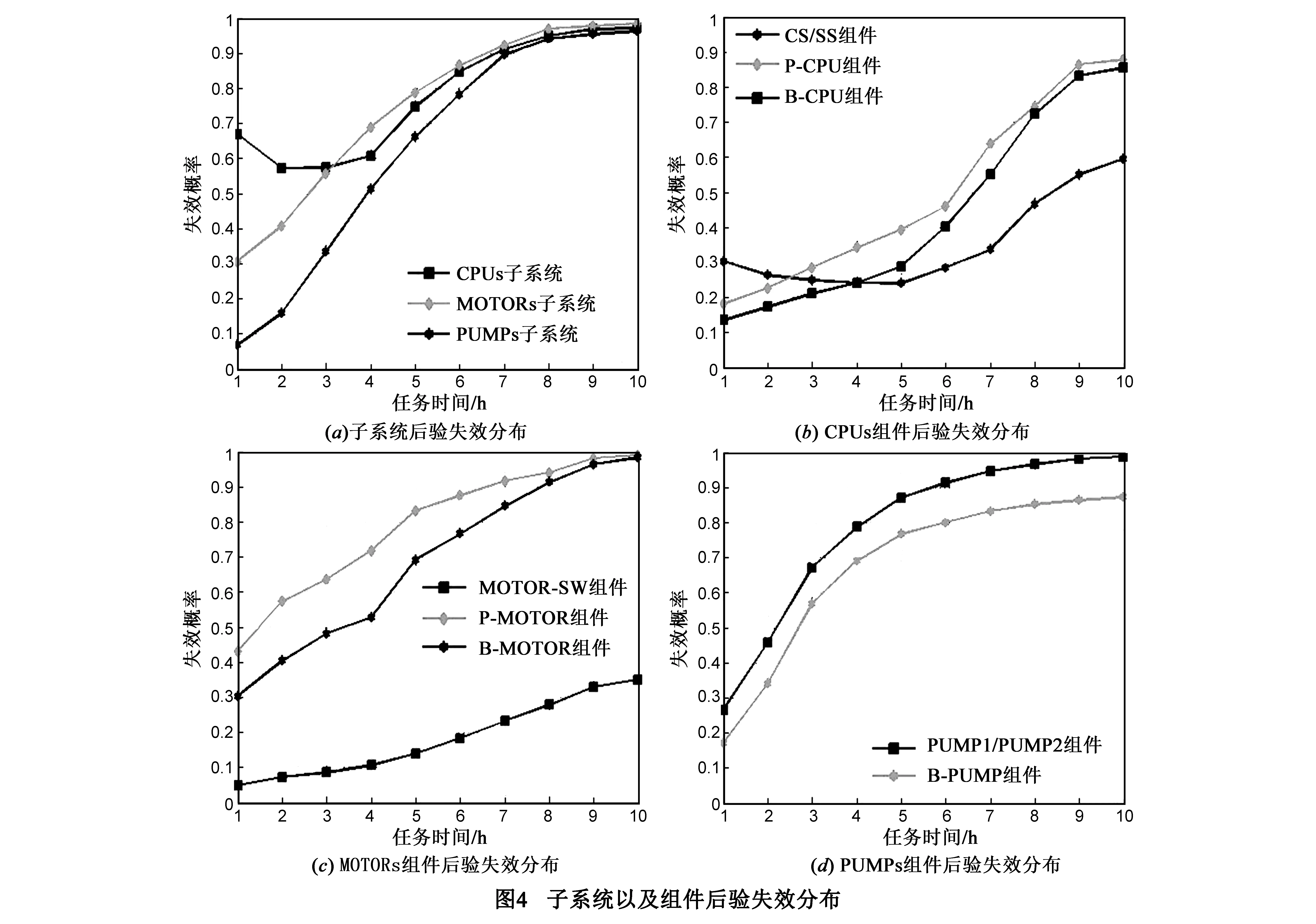
和CTMC等其他方法相比,IDTBN法能够在给定证据下进行后验概率查询.当CAS系统失效时,IDTBN计算的各子系统以及组件后验失效分布如图4所示.

表4　组件Birnbaum重要度

5　总结

IDTBN方法,克服了BN节点CPD组合爆炸缺点,消除了BN备件节点失效时间仅能是指数分布的限制,提高了分析效率和分析能力.在实验中,将IDTBN和DTBN,CTMC等方法在时间性能、计算精度方法进行比较,然后利用该方法对系统失效分布和组件重要度等安全攸关系统概率特性计算,实验结果表明,IDTBN方法的分析能力和效率优于现存的分析方法.

[1]黄志球,徐丙凤,阚双龙,等.嵌入式机载软件安全性分析标准、方法及工具研究综述[J].软件学报,2014,25(2):200-218.

HuangZQ,XuBF,KanSL,etal.Surveyonembeddedsoftwaresafetyanalysisstandards,methodsandtoolsforairbornesystem[J].JournalofSoftware,2014,25(2):200-218.(inChinese)

[2]JBDugan,SJBavuso,MABoyd.Dynamicfault-treeforfault-tolerantcomputersystems[J].IEEETransactionsonReliability,1992,41(3):363-377.

[3]JBDugan,KJSullivan,DCoppit.Developingalowcosthigh-qualitysoftwaretoolfordynamicfault-treeanalysis[J].IEEETransactionsonReliability,2000,49(1):49-59.

[4]LiudongXing,MorrissetteBA,DuganJB.Combinatorialreliabilityanalysisofimperfectcoveragesystemssubjecttofunctionaldependence[J].IEEETransactionsonReliability,2014,63(1):367-383.

[5]徐丙凤,黄志球,胡军,等.一种状态事件故障树的定量分析方法[J].电子学报,2013,41(8):1480-1486.XUBing-feng,HUANGZhi-qiu,HUJun,etal.Amethodforquantitativeanalysisofstate/eventfaulttree[J].ActaElectronicaSinica,2013,41(8):1480-1486.(inChinese)

[6]GMerle,JMRoussel,JJLesage,etal.Probabilisticalgebraicanalysisoffaulttreeswithprioritydynamicgatesandrepeatedevents[J].IEEETransactionsonReliability,2010,59(1):250-261.

[7]JunNi,WenchengTang,YanXing.Asimplealgebraforfaulttreeanalysisofstaticanddynamicsystems[J].IEEETransactionsonReliability,2013,62(4):856-872.

[8]DaochuanGe,MengLin,YanhuaYang,etal.Quantitativeanalysisofdynamicfaulttreesusingimprovedsequentialbinarydecisiondiagrams[J].ReliabilityEngineeringandSystemSafety,2015,142(10):289-299.

[9]KDRao,VGopika,VVSSRao,etal.Dynamicfaulttreeanalysisusingmontecarlosimulationinprobabilisticsafetyassessment[J].ReliabilityEngineeringandSystemSafety,2009,94(4):872-883.

[10]PeicanZhu,JieHan,LeiboLiu,etal.Astochasticapproachfortheanalysisoffaulttreeswithpriorityandgates[J].IEEETransactionsonReliability,2014,63(2):480-495.

[11]MontaniS,PortinaleL,BobbioA,etal.RADYBAN:atoolforreliabilityanalysisofdynamicfaulttreesthroughconversionintodynamicBayesiannetworks[J].ReliabilityEngineeringandSystemSafety,2008,93(7):922-932.

[12]BoudaliH,DuganJB.Adiscrete-timeBayesiannetworkreliabilitymodelingandanalysisframework[J].ReliabilityEngineeringandSystemSafety,2005,87(3):337-349.

[13]周忠宝,周经伦,孙权.基于离散时间贝叶斯网络的动态故障树分析方法[J].西安交通大学学报,2007,41(6):732-736.

ZhouZhongbao,ZhouJinglun,SunQuan.DynamicfaulttreeanalysisbasedondynamicBayesiannetworks[J].JournalofXianJiaoTongUniversity,2007,41(6):732-736.(inChinese)

[14]NKhakzad,FKhan,PAmyotte.Risk-baseddesignofprocesssystemsusingdiscrete-timeBayesiannetworks[J].ReliabilityEngineeringandSystemSafety,2013,109(1):5-17.

[15]BoudaliH,DuganJB.Acontinuous-timeBayesiannetworkreliabilitymodelingandanalysisframework[J].IEEETransactionsonReliability,2006,55(1):86-97.

[16]Yan-FengLi,Hong-ZhongHuang,YuLiu,etal.Anoveldynamicfaulttreeanalysismethod[A].TheProceedingsof2013InternationalConferenceonQuality,Reliability,Risk,Maintenance,andSafetyEngineering[C].Piscatawa:IEEE,2013.81-84.

[17]DanieleCodetta-Raiteri,LuigiPortinale.ModelingandanalysisofdependablesystemsthroughgeneralizedcontinuoustimeBayesiannetworks[A].ReliabilityandMaintainabilitySymposium(RAMS),2015Annual[C].Piscataway:IEEE,2015.1-6.

[18]XiaopengLi,NanAo,LeileiWu.Therefiningreliabilitymodelingmethodforthesatellitesystem[A].TheProceedingsof2014 10thInternationalConferenceonReliabilityMaintainabilityandSafety[C].Piscataway:IEEE,2014.484-488.

[19]王桢珍,姜欣,武小悦,等.信息安全风险概率计算的贝叶斯网络模型[J].电子学报,2010,38(2A):18-22.

WANGZhen-zhen,JIANGXin,WUXiao-yue,etal.Planningexploitationgraph-Bayesiannetworksmodelforinformationsecurityriskfrequencymeasurement[J].ActaElectronicaSinica,2010,38(2A):18-22.(inChinese)

[20]KollerD,FriedmanN.ProbabilisticGraphicalModels:PrinciplesandTechniques[M].Cambridge:MITPress,2009.

房丙午男,1974年生于安徽安庆.现为南京航空航天大学计算机科学与技术学院博士研究生,副教授.主要研究方向软件工程,软件系统安全性分析.

E-mail:bingwufang@163.com

黄志球(通信作者)男,1965 年生于江苏南京.现为南京航空航天大学教授,博士生导师,CCF杰出会员.主要研究方向为软件工程,形式化方法,软件分析与验证.

E-mail:zqhuang@nuaa.edu.cn

Quantitative Analysis Method of Dynamic Fault Tree of Complex System Using Bayesian Network

FANG Bing-wu1,2,HUANG Zhi-qiu1,LI Yong1,WANG Yong1

(1.CollegeofComputerScienceandTechnology,NanjingUniversityofAeronauticsandAstronautics,Nanjing,Jiangsu210016,China; 2.DepartmentofElectronicsandInformation,AnhuiVocationalCollegeofFinanceandTrade,Hefei,Anhui230061,China)

There exist limitations of local combinatorial explosion and only exponential distribution of spare nodes in Bayesian network(BN)-based dynamic fault tree(DFT) analysis method.First,an approach of mapping DFT into discrete-time BN is proposed in which a deterministic function instead of conditional probability tables is used to avoid local combinatorial explosion.Second,according to the failure mechanism and BN structure of spare door,we remove the limitation that the failure time of spare nodes in BN is only exponential distribution.Finally,an exact inference algorithm of DFT-based BN is presented and based on which the failure distribution of system and the importance measurement of components is calculated.Experimental results show that the proposed method can analyze and evaluate the probability characteristics of safety-critical systems effectively.

dynamic fault tree;Bayesian network;quantitative analysis;safety-critical system

2015-06-15;

2015-08-26;责任编辑:覃怀银

国家自然科学基金(No.61272083,No.61562087);安徽省教育厅自然科学基金 (No.KJ2013B009,No.KJ2015A400)

TP311

A

0372-2112 (2016)05-1234-06

电子学报URL:http://www.ejournal.org.cn10.3969/j.issn.0372-2112.2016.05.032