基于SMC的STBC-MC-CDMA信号扩频码及信息序列盲估计
2016-09-02钟兆根张立民林洪文
钟兆根,张立民,林洪文
(海军航空工程学院电子信息工程系,山东烟台 264001)
基于SMC的STBC-MC-CDMA信号扩频码及信息序列盲估计
钟兆根,张立民,林洪文
(海军航空工程学院电子信息工程系,山东烟台 264001)
针对具有空时分组码的多载波CDMA(Space Time Block Coding Multi Carrier Code Division Multiple Access,STBC-MC-CDMA)信号扩频码及信息序列的联合估计问题,结合序贯蒙特卡罗(Sequential Monte Carlo,SMC)算法和卡尔曼滤波技术,充分利用STBC和OFDM(Orthogonal Frequency Division Multiplexing)调制的正交属性,提出了一种快速的盲解扩算法.该算法通过将信号模型按不同符号路数和天线数目进行分段处理,采用卡尔曼滤波方法对均值和协方差进行迭代更新,并用一组带有权值的抽样粒子来近似建立的联合后验概率分布,根据抽样值和重要性权值大小进行参量状态估计,大大提高了算法的计算效率.理论分析和仿真结果验证了本文算法的有效性.
扩频通信;码分多址;空时分组码;序贯蒙特卡罗;扩频码;信息序列
1 引言
随着DS-CDMA(Direct Sequence,DS)技术的不断发展,传统的扩频技术因为存在处理增益和数据率之间的矛盾,从而限制了其在高速数据传输方面的应用.为了更好的满足卫星通信的需求,国外现有的卫星广泛采用WCDMA(Wide Code Division Multiple Access)通信体制,并在扩频通信中引入了多载波直接序列扩频技术,同时采用STBC进行编码,以提高数据的传输速率和增加系统的容量.因此,在非合作通信条件下,对STBC-MC-CDMA信号进行扩频码及信息序列的盲估计具有重要的理论研究与实用价值[1,2].
目前,对STBC-MC-CDMA信号的侦察处理研究仍处于起步阶段,现有的研究成果[3~6]主要是针对多载波CDMA进行的,由于该类方法不能很好地解决空时分组编码所带来的天线处理模糊问题,因此不能有效的应用于STBC-MC-CDMA系统中.文献[7]在合作条件下采用吉布斯抽样的方法对该系统信息序列和信道参数进行了有效的估计,得到了较好的结果;但针对非合作情况,文献[8,9]分别采用高阶统计量和最大似然估计方法进行处理,得到了较好的估计精度,但两种算法的计算量都比较大,且没有较好地解决天线处理模糊的问题;文献[10]采用相关矩阵的方法能很好的适应低信噪比的需求,且计算量相对较低,但其收敛速率较慢,鲁棒性较差;文献[11]采用最小均方误差自适应滤波方法进行处理,其收敛速度较快,但对信噪比的适应能力不强.因此,针对非合作时的STBC-MC-CDMA系统,如何有效的解决天线处理模糊问题、改善方法对低信噪比的适应能力和减少计算复杂度就成为该领域的研究难点.
针对上述情况,本文假设已经估计出各用户的扩频周期、码片周期和用户个数,将信号模型按不同符号路数和天线数目进行分段,采用SMC方法进行分析处理,以解决天线处理的模糊问题.首先建立频域扩频的信号模型;然后考虑时变的信道环境,将其建模成一阶的AR模型,从理论上推导出了基于SMC的各用户扩频码和信息序列联合估计算法;最后利用文献[12]给出的修正思想对算法进行修正,并充分利用空时分组码和多载波调制的正交属性,简化算法的实现过程,从而完成参数的迭代估计.仿真结果验证了算法对不同用户数、不同扩频长度和不同粒子数的适应情况,同时在低信噪比条件下,该算法能较好的对时变信道的幅度参数进行跟踪.
2 信号模型的构建
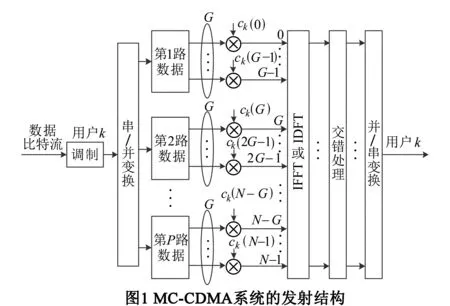
考虑一个K用户的MC-CDMA系统,各用户的传输速率相同,包含N个子载波,扩频码长度为G,在每一帧时间里有P=N/G个符号并行传输在N个子载波上.假设第k个用户的发射信号模型如图1所示,输入数据先经过调制,然后进行串/并转换成P路数据,于是第m帧的P路数据表示成向量的形式bk,m≜[bk,m(1),…,bk,m(P)]T,接着将每一路数据复制成G个相同的数据,并与扩频长度也为G的扩频序列ck(p),p=1,…,P相乘,以实现频域扩频.最后经过交错码函数T,并依次对N个数据进行傅里叶逆变换,并/串转换之后通过天线发射出去.将所有P路数据的扩频码向量组成一个N维的向量ck,即
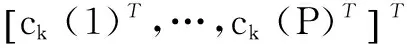
(1)
于是扩频信号也可表示成N维向量的形式

(2)
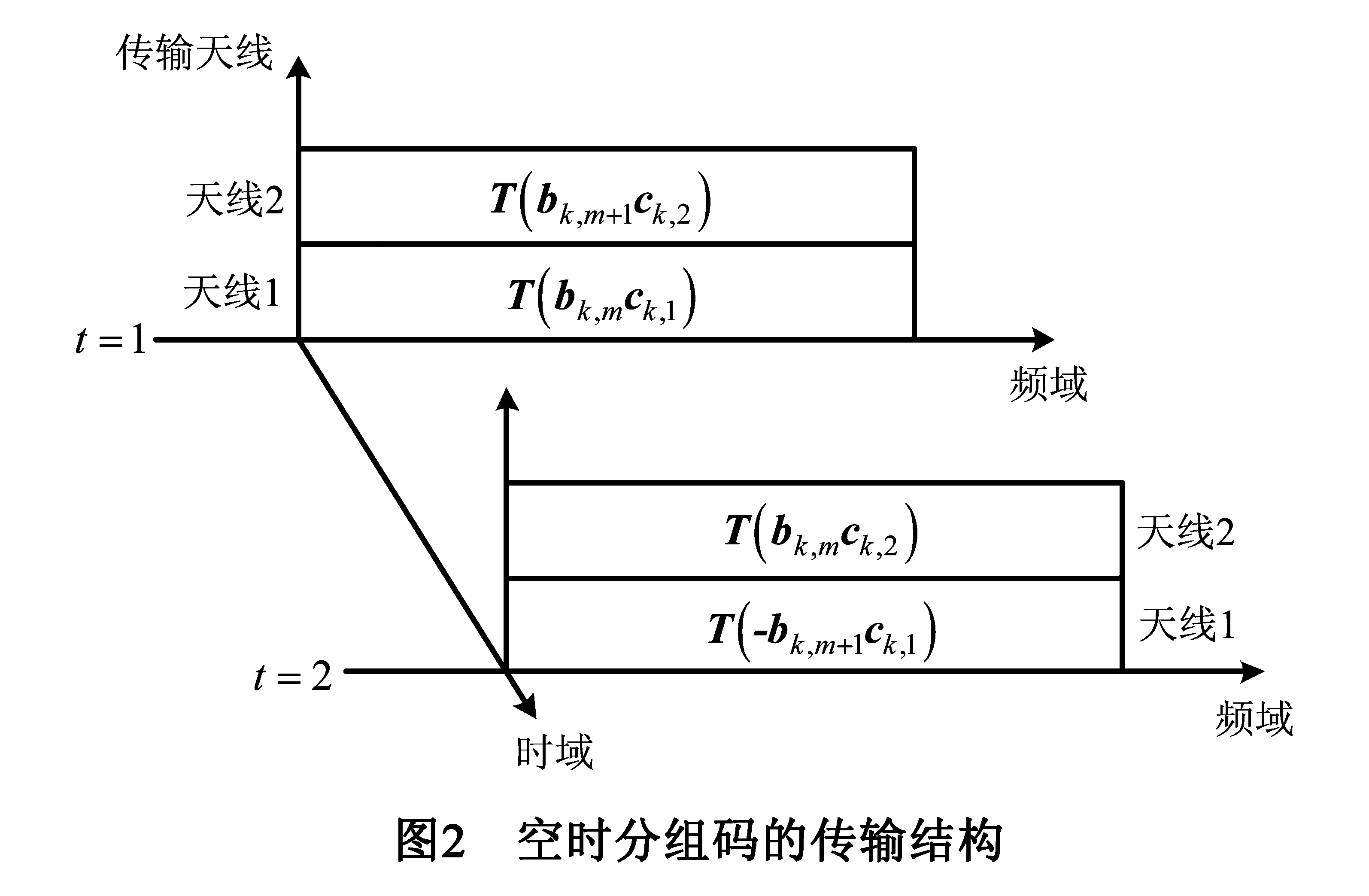
式中:符号bk,mck并不代表向量的乘积,只表示进行的扩频操作,下面用该符号来描述具有空时分组码MC-CDMA系统.采用文献[13]给出的(2×2)STBC编码方式,如图2所示,该系统一次传送两帧的数据bk,m和bk,m+1,在第一帧的时间内,扩频信号bk,mck,1经过交错处理后通过第一个天线在N个子载波上发送T(bk,mck,1),与此同时T(bk,m+1ck,2)信号由第二个天线在N个子载波上传输;在第二帧的时间内,天线1发送T(-bk,m+1ck,1),天线2发送T(bk,mck,2).由图2可知,在数据的传送过程中,天线1和天线2采用不同的扩频码向量ck,1和ck,2,这样就可有效的解决系统的天线模糊问题.
假设第k个用户的第m帧数据在第j个天线上经过多径信道传播,其表达式为
(3)
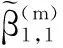
Hk,m,j(n)≜Hk,m,j(nΔf)
(4)
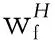
wf(n)≜[1,exp(-j2πn/N),…,
·exp(-j2πn(L-1)/N)]H
(5)
于是在接收端首先对接收信号进行匹配滤波,然后以码片速率对信号采样,再做离散傅里叶变换,并取M帧的STBC数据进行处理(此时包含2M帧的时域数据,因为在一个分组内传送2帧的数据),可得用户总数为K的离散接收信号为
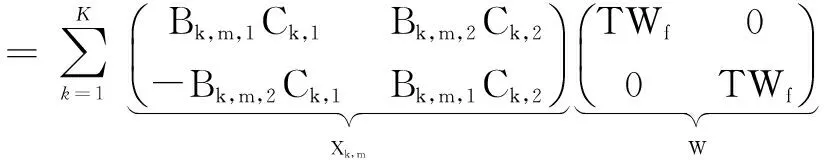
(6)
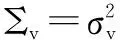
Ck,j≜diag{ck,j}N×N,
ck,j=[ck,j(1)T,…,ck,j(P)T]T, j =1,2
(7)
Bk,m,j≜diag{bk,m,j⊗IG}
=diag{bk,m,j(1)IG,…,bk,m,j(P)IG}N×N,
j=1,2
(8)

(9)
其中:⊗代表Kronecker乘积,bk,m,j,j=1,2为第m帧STBC时刻需发送的符号向量,ck,j为分配给第j个天线的扩频码向量.为减少本节算法在迭代抽样时的计算量和有效解决天线处理的模糊问题,将式(6)得到的信号模型按照不同的符号路数和天线数目进行分段处理,分别对p=1,…,P和j=1,2取不同值时采用SMC方法进行迭代抽样,其信号模型为
m=1,…,M. p=1,…,P. j=1,2
(10)
式中:Xk,m(p,j)为从矩阵Xk,m中抽取的(G×G)维子矩阵,该子矩阵由包含元素bk,m,j(p)的所有行和列组成;同理ym(p,j)、W(p,j)、hk,m,j和vm(p,j)也为从对应矩阵中抽取组成的子矩阵.由于对所有的用户K,交错函数T是相同的,于是将上式写成矩阵相乘的形式可得
ym(p,j)=Xm(p,j)Ψ(p,j)hm,j+vm(p,j)
m=1,…,M. p=1,…,P. j=1,2
(11)
式中:hm,j为KL维列向量,且有
Xm(p,j)≜[X1,m(p,j),…,XK,m(p,j)]G×KG
(12)
(13)
3 算法原理推导
为表述方便,作如下定义
bm(p,j)=[b1,m,j(p),b2,m,j(p),…,bK,m,j(p)]
(14)
Bm(p,j)=[b1(p,j),b2(p,j),…,bm(p,j)]
(15)
c(p,j)=[c1,j(p)T,c2,j(p)T,…,cK,j(p)T]T
(16)
Ym(p,j)=[y1(p,j),y2(p,j),…,ym(p,j)]
(17)
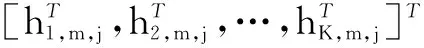
(18)
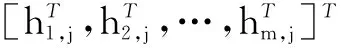
(19)
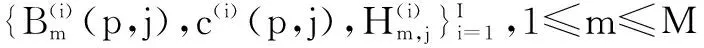
假设信道在一帧的STBC时间内是非时变的,而在不同的M内,将时变的衰落幅度建模为一阶AR模型,即
hm,j=Fhm-1,j+wm
(20)
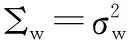
p(Bm(p,j),c(p,j),Hm,j|Ym(p,j))
=p(Hm,j|Bm(p,j),c(p,j),Ym(p,j))
·p(Bm(p,j),c(p,j)|Ym(p,j))
(21)
从上式可以看出,对未知参量的估计可以分成两部分进行,对于等号右边第一项可以根据文献[14]给出的卡尔曼滤波方法对Hm,j的均值和协方差进行迭代更新,同时针对本文的研究内容,充分利用STBC的正交特性,提出了一种快速的计算方法.第二项为低维的后验分布概率,采用SMC方法进行序贯抽样.下面对这两部分内容分别进行讨论.首先研究采用SMC方法对式(21)第二项的迭代抽样估计,为表述方便,令Zm(p,j)=(Bm(p,j),c(p,j)),zm(p,j)=(bm(p,j),c(p,j)).并选择最优的后验分布作为重要密度函数,即
(22)
经推导可得重要性权值为
(23)
于是对扩频码和信息序列等参数的估计就是通过计算式(22)和(23),从中抽取粒子和对应的重要性权值,下面给出具体的抽取方案.
首先将式(23)的预测分布分解为
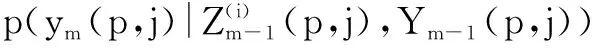
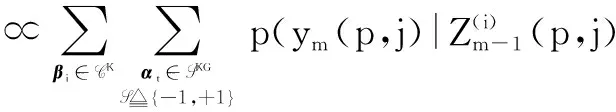
Ym-1(p,j),bm(p,j)=βs,c(p,j)=αt)
·p(bm(p,j)=βs)p(c(p,j)=αt)
(24)
式中:C为信息序列的离散有限字符集,文中假设调制样式已知,离散有限字符集的数目为V;S≜{-1,+1}为扩频码的有限字符集;p(bm(p,j)=βs)和p(c(p,j)=αt)分别为信息序列和扩频码的先验分布.同样,令
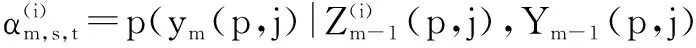
bm(p,j)=βs,c(p,j)=αt)
·p(bm(p,j)=βs)p(c(p,j)=αt)
(25)
(26)
由式(11)的信号模型可知,DI部分的分布服从复高斯分布,其表达式为
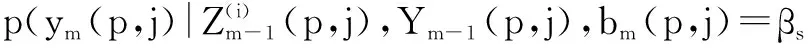
c(p,j)=αt,hm,j)
=p(ym(p,j)|bm(p,j)=βs,c(p,j)=αt,hm,j)
(27)
下面考虑DII部分的分布情况,由式(11)和(20)可知,在第m帧STBC时间内,hm,j服从复高斯分布,即
(28)
(29)
(30)
(31)
(32)
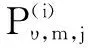
(33)
(34)
(35)
(36)
(37)
将式(27)和(37)代入(26)可得
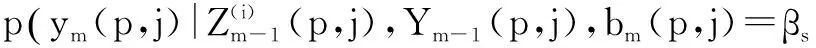
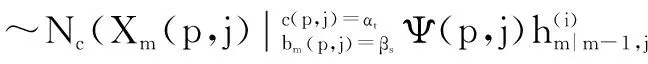
(38)
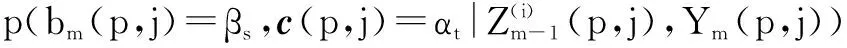
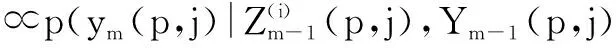
bm(p,j)=βs,c(p,j)=αt)
(39)
4 算法简化与性能分析
由式(10)和(11)的定义可知
[Xm(p,j)Ψ(p,j)]H[Xm(p,j)Ψ(p,j)]
=KG·IKL
(40)
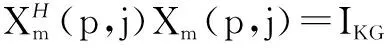
(41)
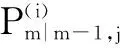
(42)

(43)
代入式(40)和(42)可得
(44)
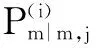
(45)
(46)
(47)
(48)
(49)
(50)
下面给出算法的具体实现步骤:

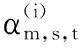
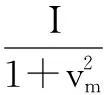
步骤5令m=m+1,重复步骤2~4进行多次迭代,最终得到各状态参量估计结果.
下面分析比较文中SMC算法和文献[8]中高阶统计量方法(Higher-OrderStatistics,HOS)的计算复杂度.本文算法的计算量主要集中在两部分:(1)对扩频码和信息序列有限字符集的搜索,对于分段的2P个数据在M帧的时间内抽取I个粒子需要的计算量为2PMNKV2K;(2)对Hm,j均值和协方差的迭代更新,需要的计算量为4PGMNK2L2.由文献[8]可知,对于与本文相同的(2×2)STBC编码方式,其算法的计算量主要集中在对协方差矩阵的特征值分解和计算峰度函数上.给出固定的输入变量,在相同的处理器上采用Matlab进行仿真,两种方法的平均计算时间如表1所示.
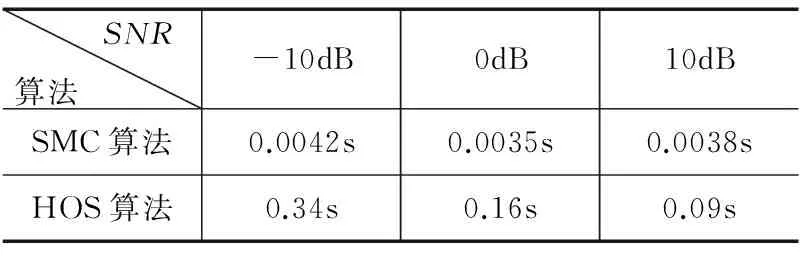
表1 两种算法的平均计算时间比较
本文算法的性能分析:(1)首先采用文献[12]的思想进行了修正,消除了SMC算法的计算量随用户数的增加成指数增长的缺陷,然后再结合空时分组码和多载波调制的正交属性,避免了新息矩阵的求逆运算,大大提高了计算效率;(2)将不同符号路数和天线数目进行分段处理,很好的解决了天线处理的模糊问题;(3)能在较低信噪比条件下实现参数的盲估计.
5 仿真实验与分析
仿真实验1验证不同用户数目时的估计性能
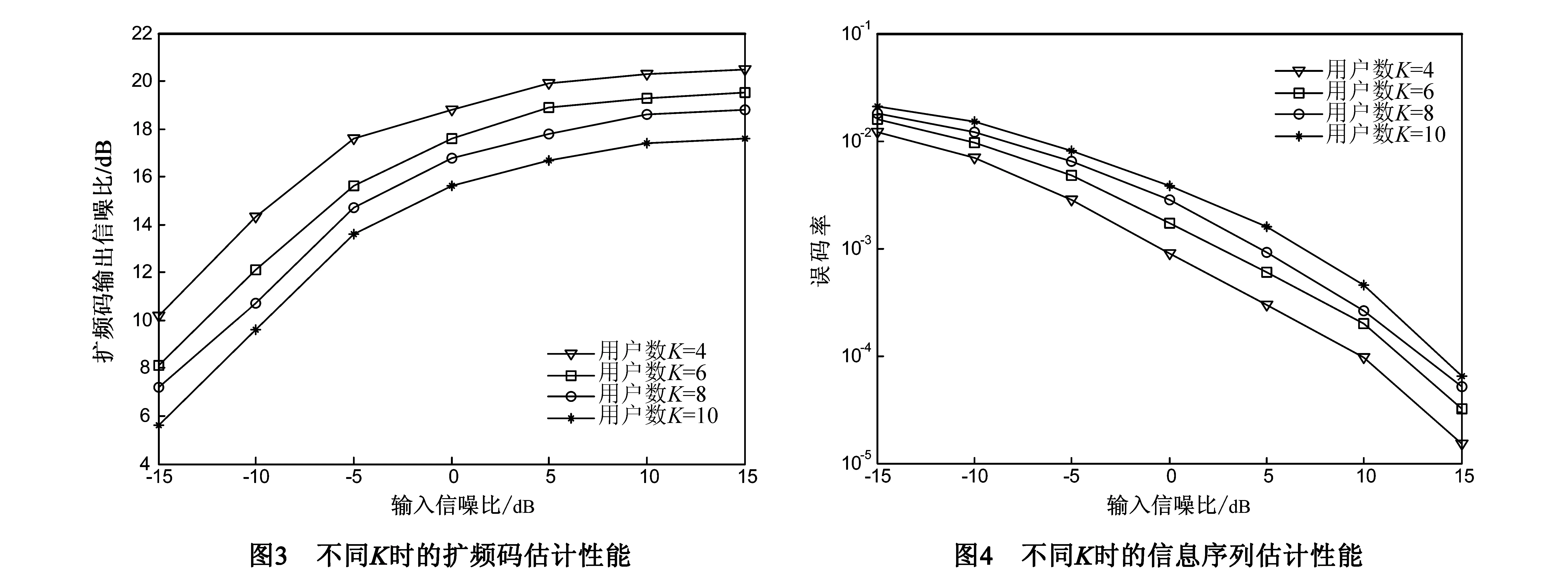
仿真条件:用户数K分别为4、6、8、10,子载波数N=128,每个用户在第p路数据上(p=1,2)的扩频码为长度G=64的随机序列,各用户的多径路数均为L=3,将时变信道衰落幅度建模成一阶AR模型,即hm,j=Fhm-1,j+wm,取F=0.999IKL,wm为零均值,协方差矩阵为Σw=0.01IKL的复高斯分布,采用M=200帧的STBC数据进行处理,输入信噪比变化范围为-15dB到15dB,算法迭代过程中取粒子数I=100.
图3和图4分别为用户数目K为4、6、8、10时,本文算法得出的扩频码和信息序列估计性能随输入信噪比变化的曲线.在多用户情况下,输出信噪比和误码率的计算为对所有用户的扩频码和信息序列粒子抽样值求平均得到,且图3中的扩频码输出信噪比是对两个天线的结果求平均后获得.仿真结果表明,在不同用户数目时,本节算法能在较低信噪比条件下盲估计出扩频码和信息序列,当信噪比大于-5dB,用户数不超过10时,恢复出的扩频码平均输出信噪比大于13dB,所有用户的信息序列估计误码率均低于10-2.
仿真实验2验证不同扩频长度和不同粒子数时的估计性能
仿真条件:K=4,子载波数N=128,扩频码长度G分别取16、32、64、128,迭代过程中分别取粒子数I为50、100、200.其它参数与仿真实验1相同.
图5和图6分别给出在不同G时,粒子数I=100,扩频码和信息序列的估计性能.从图可以看出,随着G的增加,序列的估计性能随着提高.其主要原因是在迭代过程中,分组的路数越多,信号间产生交叠的概率就越大,从而导致算法的性能降低.图7给出G=64,粒子数I分别为50、100、200时信息序列误码率随输入信噪比变化曲线.由图可以看出,粒子数越大,其估计性能越好,但是计算量也成倍增加,因此在选择粒子数时应折中考虑.

仿真实验3验证算法对时变信道的跟踪估计性能
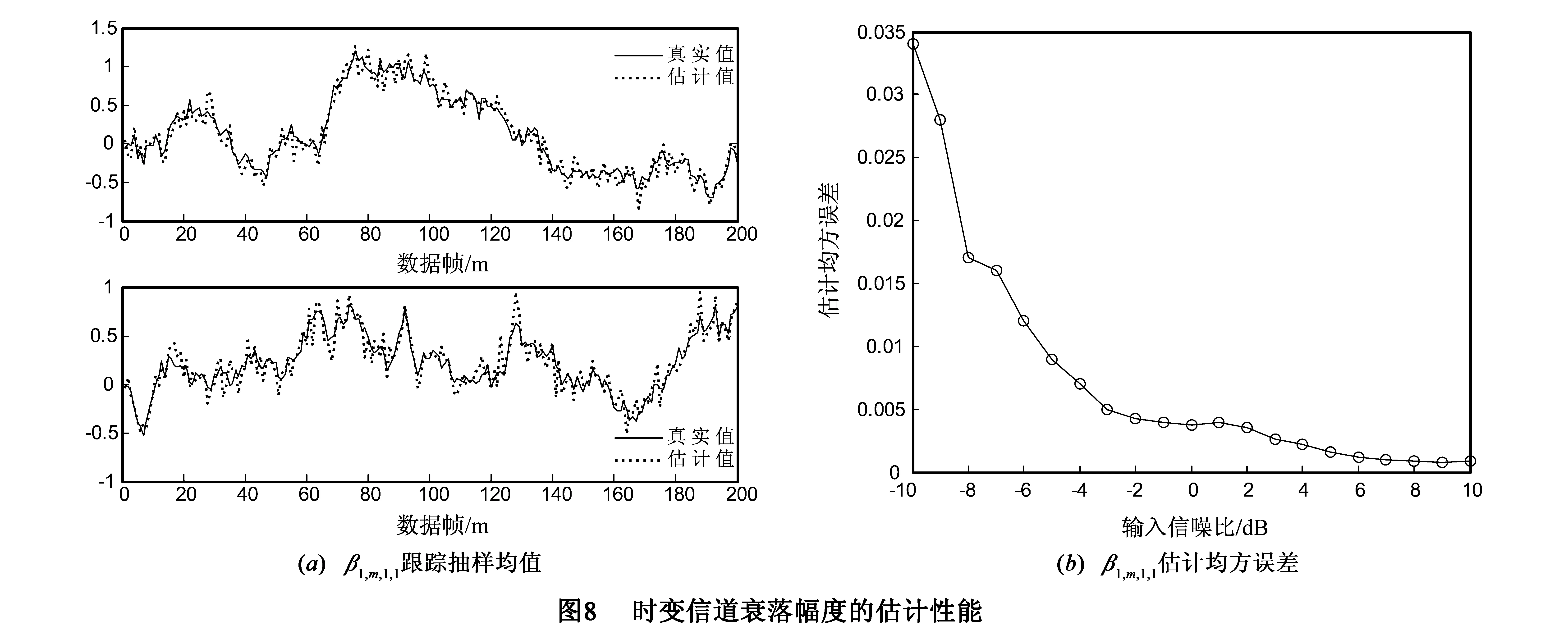
仿真条件:本次实验的仿真条件与实验1基本相同,实验主要验证用户数K=4时的信道估计性能.
图8(a)给出了信噪比为-6dB时时变衰落信道幅度β1,m,1,1的跟踪抽样均值;图(b)给出了不同信噪比条件下,仿真次数为1000,对M=200帧数据计算均方误差所得的结果.仿真结果表明,在低信噪比条件下,本文算法能够较好的对信道幅度参数进行跟踪.
6 结论
本文以STBC-MC-CDMA信号为研究对象,为解决天线处理模糊问题,在分析信号模型的基础上,按照不同的符号路数和天线数目进行分段处理,分别采用SMC方法进行扩频码及信息序列的迭代抽样估计.该算法考虑时变的衰落信道环境,充分利用空时分组码和多载波的正交性,结合卡尔曼滤波方法简化算法的执行流程,有效的降低了算法的计算复杂度.仿真结果验证了本文算法的估计性能.通过对多速率的STBC-MC-CDMA信号建模可以发现,与文中的单速率模型相似,区别主要在于对观测信号的抽取上.因此,在接下来的研究中,可以将本文的方法进行有效的扩展,应用在多速率的系统中.
[1]Mohamed Marey,Octavia A Dobre,Robert Inkol.Classification of space-time block codes based on second-order cyclostationarity with transmission impairments[J].IEEE Transactions on Wireless Communications,2012,11(7):2574-2584.
[2]He Jin,Ahmad M O,Swamy M N S.Joint space-time parameter estimation for multicarrier CDMA systems[J].IEEE Transactions on Vehicular Technology,2012,61(7):3306-3311.
[3]Nzéza C N,Berbineau M,Moniak G,et al.Blind MC-DS-CDMA parameters estimation in frequency selective channels[A].Workshops of IEEE Global Telecommunications Conference[C].Honolulu,Nov 2009:1-6.
[4]Fu P W,Chen K C.Rate.Sub-carrier,and power allocations for multi-carrier CDMA with LMMSE multiuser detection[J].IEEE Transactions on Wireless Communications,2007,6(5):1574-1580.
[5]Bangwon Seo.SINR lower bound based multiuser detector for uplink MC-CDMA systems with residual frequency offset[J].IEEE Communications Letters,2012,16(10):1612-1615.
[6]Wang Shuai,et al.Joint timing and channel estimation for band limited long-code-based MC-DS-CDMA:A low-complexity near-optimal algorithm and the CRLB[J].IEEE Transactions on Communications,2013,61(5):1998-2011.
[7]Yang Zigang,Lu Ben,Xiaodong Wang.Bayesian monte carlo multiuser receiver for space-time coded multi-carrier CDMA systems[J].IEEE Journal on Selected Areas in Communications,2001,19(8):1625-1637.
[8]Choqueuse V,et al.Blind channel estimation for STBC systems using higher-order statistics[J].IEEE Transactions on Wireless Communications,2011,10(2):495-505.
[9]Choqueuse V,Marazin M,Collin L,et al.Blind recognition of linear space-time block codes:A likelihood-based approach[J].IEEE Transactions on Signal processing,2010,58(3):1290-1299.
[10]Tsui-Tsai Lin,Fuh-Hsin Hwang.MCMOE-based CFO estimator aided with the correlation matrix approach for alamouti’s STBC MC-CDMA downlink systems[J].IEEE Transactions on Vehicular Technology,2012,61(8):3790-3795.
[11]Bangwon Seo,et al.Fast convergent LMS adaptive receiver for MC-CDMA systems with space-time block coding[J].IEEE Communications Letters,2010,14(8):737-739.
[12]Giremus A,Grivel E,Grolleau J,et al.A rao-blackwellized particle filter for joint channel/symbol estimation in MC-DS-CDMA systems[J].IEEE Transactions on Communications,2010,58(8):2292-2304.
[13]S M Alamouti.A simple transmit diversity technique for wireless communications[J].IEEE Journal on Selected Areas in Communications,1998,16(8):1451-1458.
[14]Balakumar Balasingam.Computationally efficient blind-adaptive algorithms for multi-antenna systems[D].Mcmaster University,Canada:2008.
[15]Qian Yu,et al.Modified SMC method of blind multiuser detection for DS-CDMA systems over fading channels[J].Wireless Personal Communications,2007,43:1339-1349.

钟兆根男,1984年出生,江西南昌人,博士,讲师,主要研究领域为通信侦察和空间信息对抗.
E-mail:zhongzhaogen@163.com

张立民(通信作者)男,1966年出生,辽宁开原人,教授,博士生导师,主要研究领域为卫星信号处理、武器系统仿真等.
E-mail:iamzlm@163.com
Blind Estimation of Spreading Codes and Information Sequences for STBC-MC-CDMA Signals Based on SMC
ZHONG Zhao-gen,ZHANG Li-min,LIN Hong-wen
(DepartmentofElectronicsandInformationEngineering,NavalAeronauticalandAstronauticalUniversity,Yantai,Shandong264001,China)
To deal with the problem of blind estimation of spreading codes and information sequences for space-time block coded multi-carrier CDMA signals,combined with SMC (Sequential Monte Carlo) and Kalman filtering techniques,this paper introduces a fast blind despreading algorithm by making full use of the orthogonality property of the STBC and the OFDM multi-carrier modulation.Firstly,the proposed algorithm segments the signal model through different symbols and antennas.Secondly,use Kalman filtering method to update the mean and covariance iteratively.Then,use a set of properly weighted samples to approximate the joint posterior distribution,Finally,exploit these samples to estimate the quantity of interest,which improve the computational efficiency greatly.The theoretical analysis and simulation results verify the effectiveness of the proposed algorithm.
spread spectrum communication;code division multiple access;space-time block coding;sequential monte carlo;spreading code;information sequence
2014-09-22;
2015-05-15;责任编辑:马兰英
国家自然科学基金(No.91538201);泰山学者工程专项经费资助(No.ts201511020)
TN911.7
A
0372-2112 (2016)05-1025-07
电子学报URL:http://www.ejournal.org.cn10.3969/j.issn.0372-2112.2016.05.003
