一种新的基于复指数函数映射的盲均衡算法
2016-09-02高惠娟段美怡张建秋
饶 伟,高惠娟,段美怡,张建秋
(1.复旦大学信息科学与工程学院,上海 200433;2.南昌工程学院信息工程学院,江西南昌 330099)
一种新的基于复指数函数映射的盲均衡算法
饶伟1,2,高惠娟2,段美怡2,张建秋1
(1.复旦大学信息科学与工程学院,上海 200433;2.南昌工程学院信息工程学院,江西南昌 330099)
定义了一个新的复指数函数将典型的16-QAM非常模信号的实部和虚部分别映射至单位圆上.然后利用映射后星座坐标的实部和虚部之间的关系建立代价函数,从而提出了一种新的盲均衡算法.新算法克服了著名的恒模盲均衡算法及其典型的改进算法在对非常模信号均衡时稳态误差大的缺点.通过理论证明验证了新算法在无噪声环境下稳态均方误差为0;通过仿真实验验证了新算法在有噪环境下比恒模及其改进算法具有更低的稳态均方误差.
盲均衡;恒模算法;复指数代价函数
1 引言
在数字传输系统中受信道带宽有限及多径传输的影响,接收信号中会存在码间干扰(Intersymbol interference,ISI),致使信号产生严重失真[1].因此在接收端常采用盲均衡技术[2,3]来消除或减少ISI,其中恒模盲均衡算法[4](Constant Modulus Algorithm,CMA)因其强鲁棒性和易于实现性[3,5]而被广泛使用与研究[6,7].在发射端为了提高信道带宽的利用率,常采用高阶正交幅度调制(Quadrature Amplitude Moduluation,QAM)信号[8,9].对于低阶QAM(4-QAM)信号,基于CMA的T/2分数间隔均衡器(Fractionally Spaced Equalizer,FSE)在无信道噪声环境下能实现迫零均衡[5,10].而对于高阶QAM信号,如16-QAM信号,均衡器会呈现出相对较大的误调,致使算法稳态均方误差(Mean Square Error,MSE)大,收敛速度慢.为了克服这一缺点,可以先利用CMA使接收信号的眼图睁开,然后切换到判决引导(Decision-directed,DD)算法来进一步减小残留误差[11,12].但是只有当CMA的输出误差足够小时才能保证切换成功,而在实际环境中CMA往往达不到要求[13].又或者采用软切换的方法[13,14]在稳态MSE和切换的可靠性上进行折衷处理.但是这种方法需要做大量的判决处理,计算复杂度大幅提升.为了能够减小CMA的稳态误差,近年来提出了例如融入了粒子群优化以及正交小波变换的盲均衡[15],或者基于电域反馈神经网络的自适应盲均衡方法[16],或者基于混合误差函数的盲均衡[17~19];又或者针对CMA和DD切换方式提出新的切换方法[20]或降低其计算复杂度[21].上述算法的稳态MSE较CMA虽有所减少,但对于非常模信号却仍无法收敛至0.为此,文献[22]提出了一种基于坐标变换的盲均衡算法,并通过DSP加以实现[23].但是这种变换并不是一一映射,这对算法的鲁棒性有一定影响.因此作者在文献[24]中定义了一种一一映射的变换方式,并提出了一种类似于Sign-GA[25]准则的代价函数与变换方式相配合.但是该算法在信道失真严重或者信噪比较低的情况下性能提升不明显[24].
本文针对典型的16-QAM非常模信号定义了一种新的一一映射的复指数函数,该函数能将16-QAM信号的实部和虚部分别映射至2个单位圆上,再利用各单位圆上信号坐标的实部和虚部之间的关系建立起一个全新的代价函数,从而提出了一种新的盲均衡算法.该算法克服了传统盲均衡算法对非常模信号均衡时稳态误差大的缺点,并且新算法在信道失真严重或者信噪比较低的情况下依然具有良好的性能.利用理论证明的方式验证了在无噪声环境下新算法的稳态MSE为0.同时,采用Rice大学信号处理数据库(SPIB)中的微波信道[26]以及严重失真信道[27]模型,在无噪和有噪环境下将新算法与具有代表性的盲均衡算法:CMA、CMA+SDD[14]、MCMA[28]、MMA[29]、文献[24]算法,进行仿真实验对比,实验结果进一步验证了新算法的优越性能.
2 T/2分数间隔盲均衡
研究T/2分数间隔均衡器[5],其结构模型如图1所示.

图中s(k)为发射信号;长度为2M的信道冲激响应c分成奇偶两部分ce、co;长度为2N的均衡器抽头系数向量f也分成奇偶两部分fe、fo,形成2个子均衡器.k时刻2个子均衡器的输入向量分别为xo,k=[xo(k)…xo(k-N+1)],xe,k=[xe(k)… xe(k-N+1)];y(k)为均衡器输出信号.令xk=[xo,kxe,k],fk-1=[fe,k-1fo,k-1],则
(1)
式中,T表示取转置操作.
在T/2-FSE结构中可以使用不同的盲均衡算法,这里以应用最为广泛的CMA[4,5]为例.CMA的代价函数定义为
(2)
式中,R2为发射信号的统计模值,定义为
R2=E[|s(k)|4]/E[|s(k)|2]
(3)
利用瞬时随机梯度下降法对f进行更新以最小化代价函数,则f更新公式为
(4)
式中,▽表示求瞬时梯度操作,eo(k)为误差函数项.将代价函数(2)代入上式得CMA误差函数项
eo(k)=y(k)[R2-|y(k)|2]
(5)
由代价函数式(2)可知,CMA的目的是期望每个输出信号的幅度模值|y(k)|与|R|相等,此时代价函数被最小化为零,误差函数项(5)为零,均衡器抽头系数停止更新.当均衡器稳定后的输出信号满足|y(k)|=|R|=|s(k)|时,称之为理想均衡,此时CMA稳态MSE为0.对于常模信号,基于CMA的T/2-FSE(简称CMA)在无噪声环境下,可以实现理想均衡;但对于非常模信号,CMA无法实现理想均衡[5,30].
3 新算法
非常模信号的幅度模值与CMA统计模值的平方根不相等是导致CMA稳态误差大,收敛速度慢的主要原因之一.因此,针对典型的16-QAM非常模信号,通过映射处理再结合适当的代价函数相配合,从而克服上述缺陷:
考虑到16-QAM信号的实部和虚部均与4阶脉冲幅度调制(Pulse-amplitudeModulation,PAM)信号相同.因此,先以4-PAM非常模实信号为例引出新算法,然后在通过对实部和虚部分开均衡的方法将新算法引入16-QAM信号中.
针对4-PAM信号定义复指数映射函数
(6)
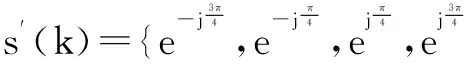
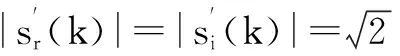
(7)
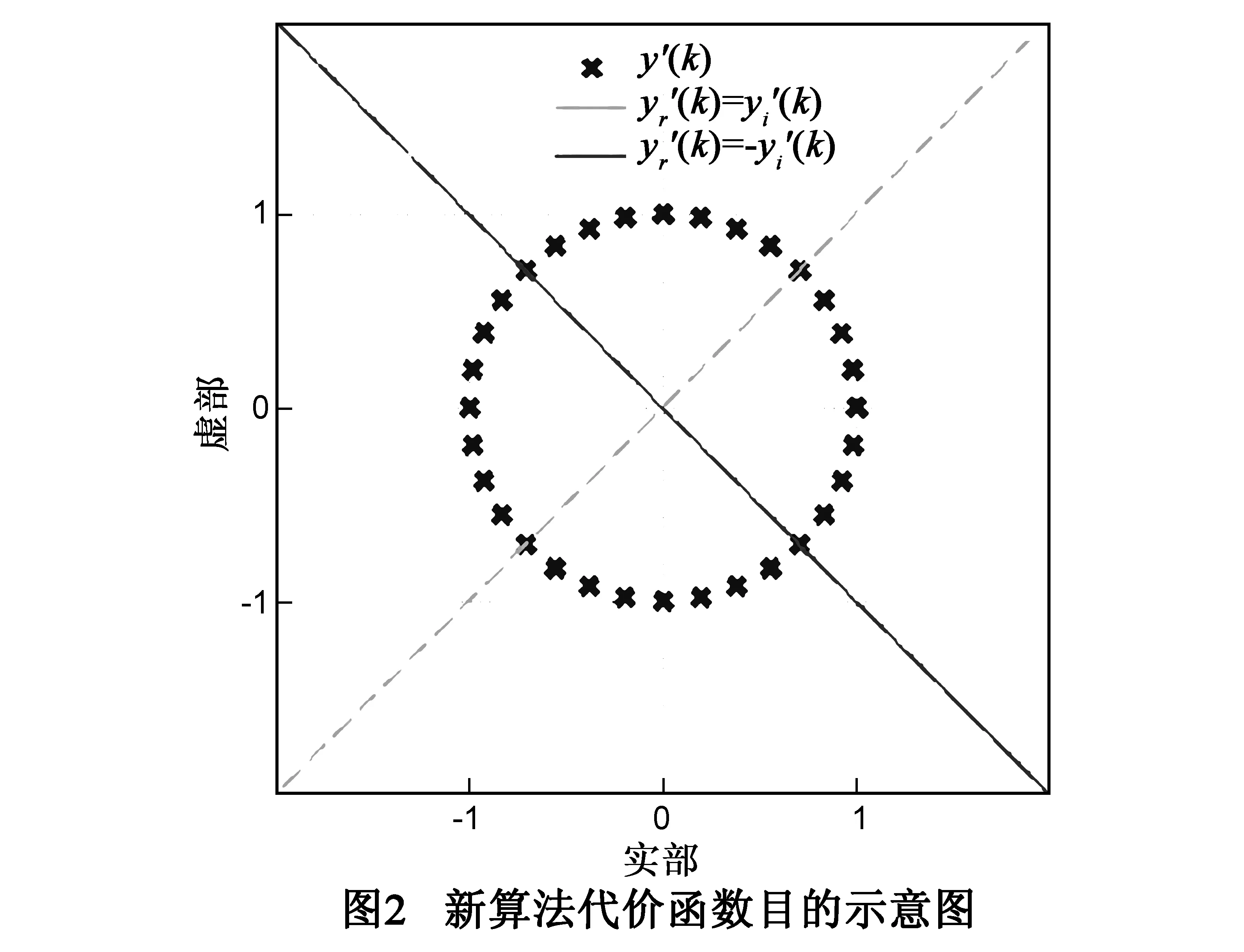
式中,下标r和i分别代表取实部和虚部操作.因此建立新算法代价函数
(8)

⟹y′(k)
(9)
这正是我们所期望的理想均衡.
结合式(4)、(6)、(8)得适用与4-PAM信号的新算法误差函数项
(10)
式中,sgn[·]为符号函数.
由于16-QAM信号星座可以由2个正交的4-PAM信号星座组合而成,因此利用实部和虚部分开均衡处理的思想可得适用于16-QAM信号的盲均衡新算法:
(1)代价函数为
(11)
(2)将式(11)带入式(4)得新算法误差函数项
(12)
4 新算法性能分析
4.1新算法稳态MSE性能分析
应用一种反馈式性能评估方法[30],对新算法收敛后的稳态MSE进行评估,其核心计算式为[30]
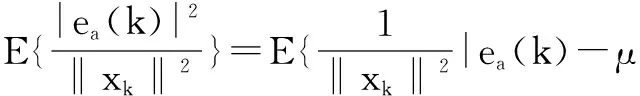
(13)
(14)
通过该式,可以得到算法的稳态MSE:E{|ea|2}.
在进行评估之前,先提出以下合理假设[30]:
(a)稳态时,发射信号s与误差ea相互独立,即E{s*ea}=0.
(b)稳态时,μ2‖x‖2与y相互独立,μ2‖x‖2与ea相互独立.

(1)计算T1
将新算法误差项(12)代入T1得
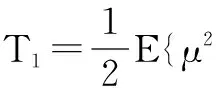
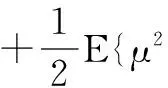
(15)
利用余弦函数的麦可劳林展开式
(16)
并将yr=sr-ear、yi=si-eai[30]代入T1,再结合假设得

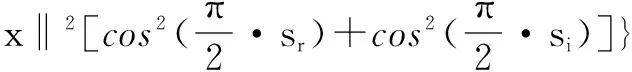
(17)
(2)计算T2
(18)

(19)
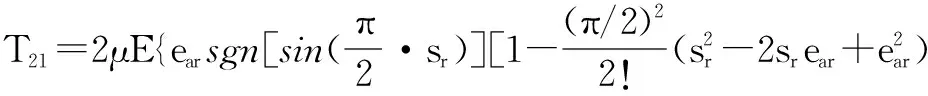
(20)
当μ、ear足够小时,忽略包含ear的3次及更高次幂项,则
(21)
利用式(16)及正弦函数的麦可劳林展开式
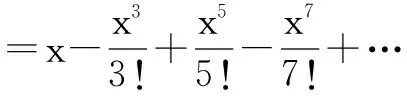
(22)
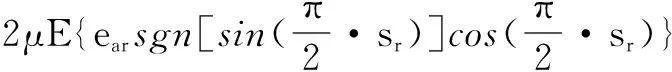
(23)
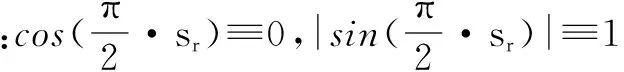
(24)
同理可得
(25)
所以
T2=T21+T22≈πμE{|ea|2}
(26)
(3)稳态MSE
由T1=T2,并结合式(17)、(26)得
E{|ea|2}
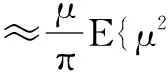
(27)
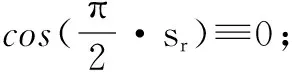
E{|ea|2}≈0
(28)因此,针对16-QAM非常模复信号,新算法稳态MSE约为0.
针对4-PAM非常模实信号,在分析其稳态MSE时可以把它看成虚部为0的16-QAM信号,因此易得其稳态MSE

(29)
可见,无论是4-PAM非常模实信号还是16-QAM非常模复信号,新算法收敛后稳态MSE约为零,而CMA稳态MSE不为零[5,30].
4.2新算法与文献[24]算法性能对比分析
新算法与文献[24]算法属同一类算法,因此有必要对这两种算法进行对比分析(这里以4-PAM信号为例),详见表1.
可见,新算法的映射函数和文献[24]相比虽然只是一个π/4的变化,但是后续匹配代价函数的建立是全新的且它给算法性能,包括计算量、收敛速度、稳态MSE、工作环境的适应性等,带来了较大的提升.
5 计算机仿真分析
为了进一步验证新算法的性能,我们将新算法与5个极具代表性的盲均衡算法:CMA、CMA+SDD[14]、MCMA[28]、MMA[29]以及文献[24]中的算法,进行仿真实验对比.首先,通过无噪仿真实验来验证前面对新算法所做出的理论分析.其次,利用Rice大学信号处理数据库(SPIB)中的微波信道模型在不同信噪比的情况下,对上述算法进行仿真实验分析.最后,通过仿真实验的方式来说明即便是在失真较为严重的信道环境[27]中,新算法同样能够体现出其优越的性能.

表1 新算法与文献[24]算法对比分析表(以4-PAM为例)
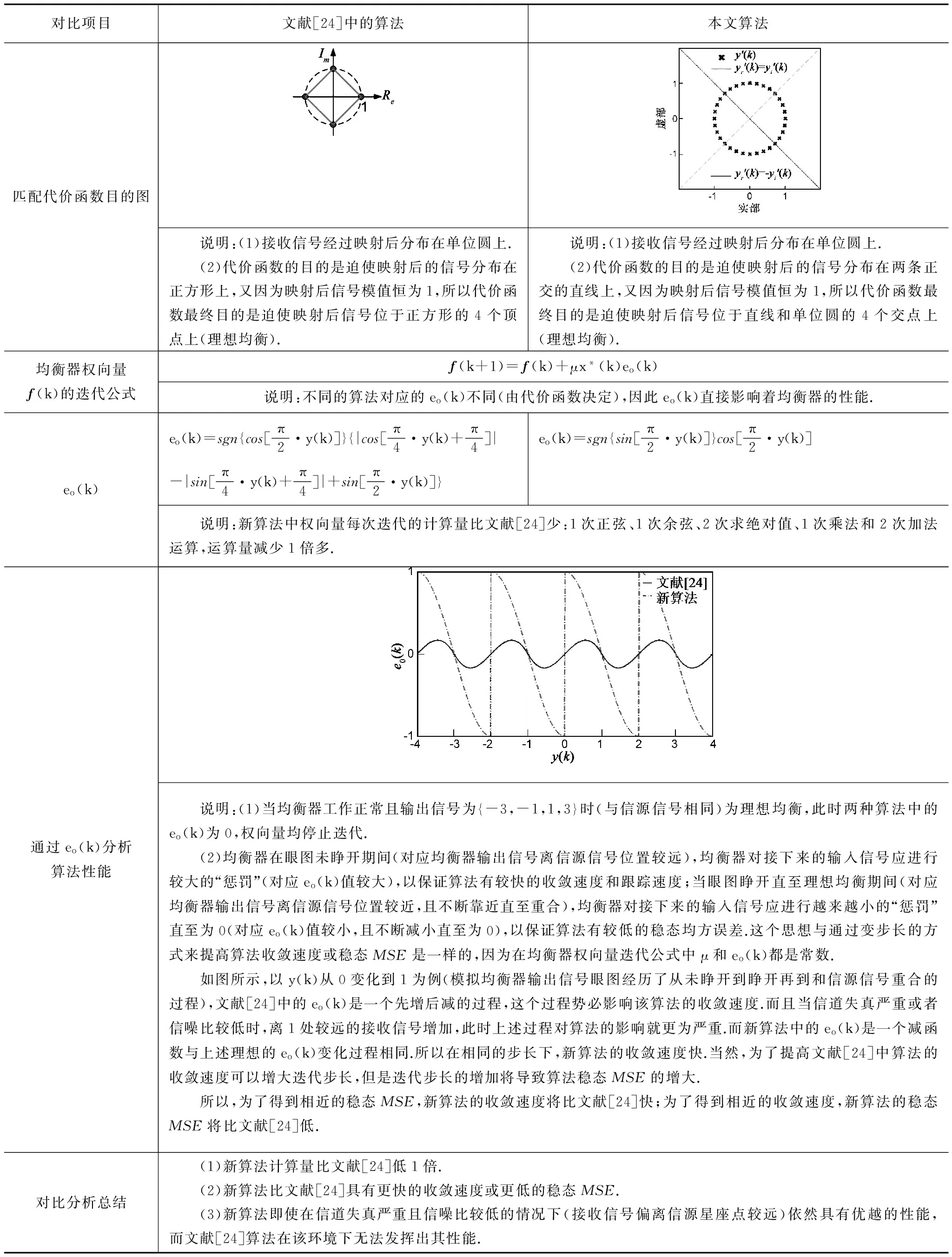
续表
5.1无噪声环境下仿真实验
该仿真实验中,无噪声信道的脉冲响应为c=[-0.0901,0.6853,0.7170,0.0901][30],发射信号为16-QAM信号.所有算法均采用T/2分数间隔均衡器结构,各子均衡器抽头个数均为5.新算法的步长均为0.001;文献[24]中算法的步长为0.002;CMA和MMA的步长均为0.000016;MCMA中步长为0.000016,另一个参数取值为100;CMA+SDD中CMA部分步长为0.000016,SDD部分步长为0.0016,另一个参数取值为0.3.仿真结果如图3所示,当各算法收敛后新算法和文献[24]算法的输出稳态MSE约为-300dB,即MSE≈10-30近似为0,远远小于其它几种算法的稳态MSE.但需要注意的是,虽然新算法和文献[24]算法均能得到近似为0的稳态MSE,但是在保证这两种算法稳态MSE近似相等(实际上新算法稳态MSE略低)的前提下新算法收敛速度比文献[24]快了近1倍.
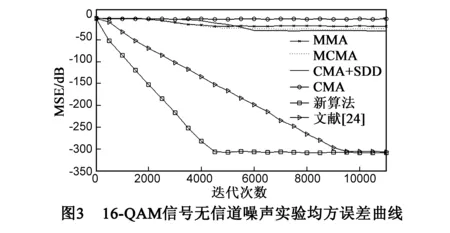
5.2有噪声环境下微波信道仿真实验
采用Rice大学信号处理数据库(SPIB)中的微波信道模型chan2[26],在不同信噪比下对比分析各算法的稳态MSE,且实验过程中以各算法经过大约1500次迭代后收敛为前提.各算法参数设置及仿真结果如表2所示.
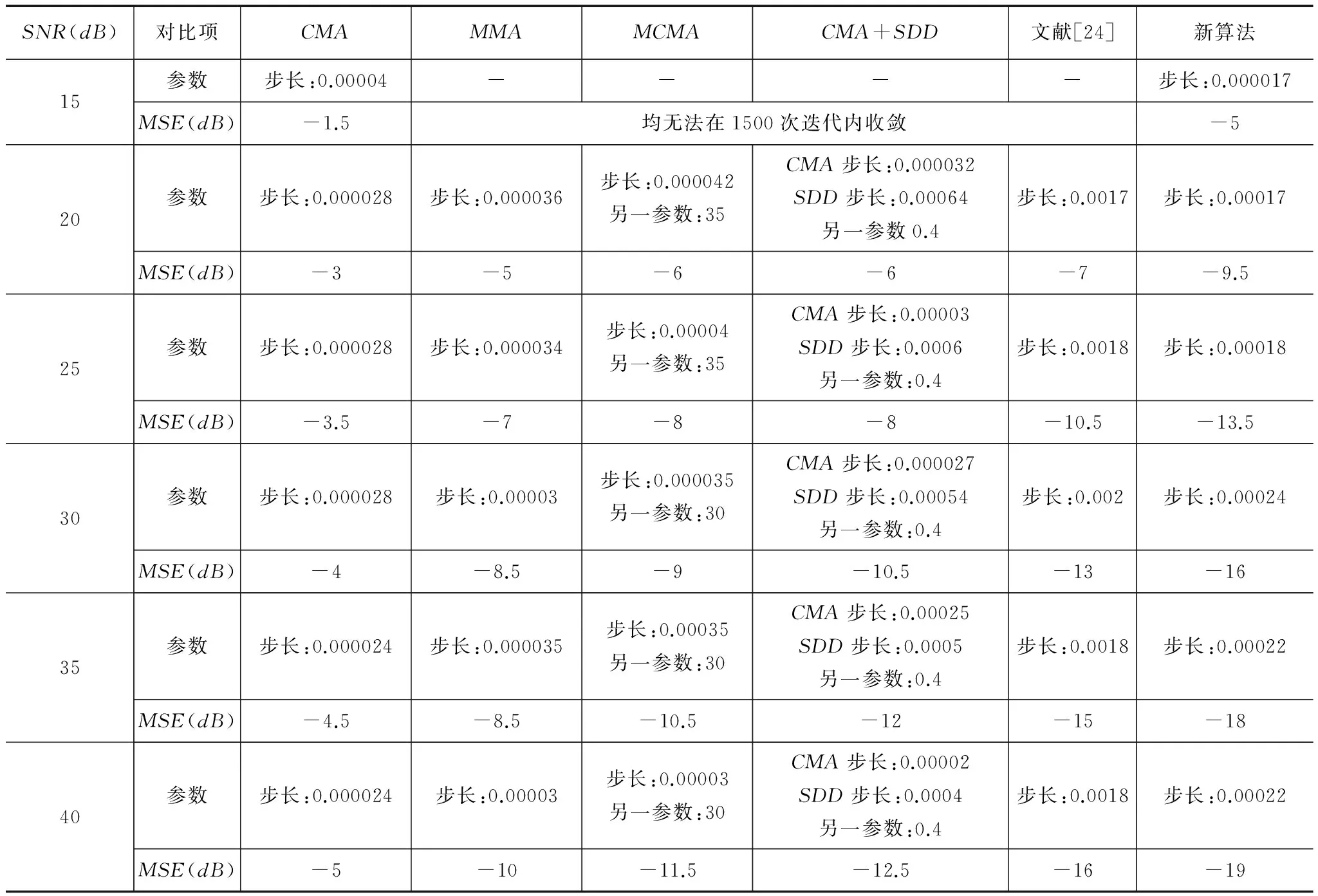
表2 各算法在相同收敛速度(约1500次迭代)不同SNR情况下的仿真结果
可见,新算法在不同的信噪比下均具有最小的稳态MSE且比次优算法(文献[24])小约1倍;此外,在低信噪比下(如20dB)文献[24]算法与已有算法相比优势不够明显(这与文献[24]中的分析是一致的),但是新算法却依然能够体现出其优越的性能,该结论同样体现在接下来的仿真实验中.
5.3有噪声环境下严重失真信道仿真实验
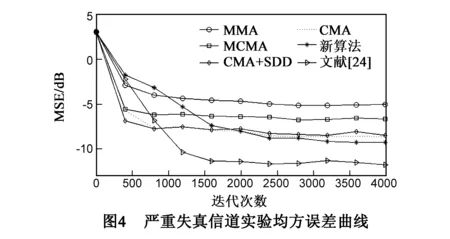
采用文献[27]中失真最严重的信道模型对新算法的适用性进行仿真验证.发射信号为16-QAM信号,信噪比为20dB.所有算法均采用T/2分数间隔均衡器结构,各子均衡器抽头个数均为9.CMA、MMA、文献[24]算法、新算法的步长分别为0.000032、0.0002、0.003、0.0004;MCMA中步长为0.0001,另一个参数取值为40;CMA+SDD中CMA部分步长为0.00004,SDD部分步长为0.0008,另一个参数取值为0.8.仿真结果如图4所示:新算法收敛后的稳态MSE约为-12dB≈0.0631,比文献[24]算法的-9dB≈0.1259减少约一倍多.此外,就此次实验而言,其中的两种算法MCMA和CMA+SDD在5.1和5.2中后者的性能要略优于前者,而在5.3中正好相反.造成这个问题的一个重要原因是这两种算法除步长外还受其它参数控制,且参数和步长对算法性能的影响并不相互独立,不同的参数组合对算法性能会产生不同的影响.但是新算法不存在这种多参数的选择问题,从这个角度讲新算法除了稳态MSE最低以外,其在操作实现上也要比MCMA和CMA+SDD简单得多.
6 结论
传统CMA及其改进的盲均衡算法虽然能有效克服多径衰落,但是对于非常模信号均衡效果并不理想.本文详细分析了产生上述问题的一个重要原因,并据此针对典型的16-QAM非常模信号提出了一种基于复指数映射的盲均衡新算法.利用理论证明和仿真实验验证了新算法在无噪声环境下稳态MSE能收敛至零;在有噪环境下通过仿真实验验证了新算法同样具有比同类算法更加优越的性能及强可操作性.
虽然新算法只适用于4-PAM和16-QAM信号,但是却能为进一步提高现有盲均衡的性能提供一条新的途径.例如对于其它类型非常模调制信号以及更高阶的QAM信号,如果能找到适合的映射对象以及与之相匹配的代价函数,那么盲均衡的性能可以得到很大提升.
[1]Simon Haykin.郑宝玉,等.自适应滤波器原理(第四版)[M].北京:电子工业出版社,2010:188-189.
[2]张玲,张贤达.MIMO-OFDM系统的盲信道估计算法综述[J].电子学报,2007,35(6A):1-6.
ZHANG Ling,ZHANG Xian-da.An overview of blind channel estimation algorithms for MIMO-OFDM systems[J].Acta Electronica Sinica,2007,35(6A):1-6.(in Chinese)
[3]孙云山,等.改进恒模盲均衡在医学CT图像盲恢复中的应用[J].仪器仪表学报,2012,33(4):878-884.
Sun Yunshan,et al.Application of improved constant module blind equalization algorithm in medical CT image blind restoration[J].Chinese Journal of Scientific Instrument,2012,33(4):878-884.(in Chinese)
[4]D Godard.Self-recovering equalization and carrier tracking in two dimensional data communication systems[J].IEEE Transactions on Communications,1980,28(11):1867-1875.
[5]C R Johnson Jr,P Schniter,et al.Blind equalization using the constant modulus criterion:a review[J].Proceedings of the IEEE,1998,86(10):1927-1950.
[6]Shafayat Abrar,Anum Ali,Azzedine Zerguine,Asoke K.Nandi.Tracking Performance of Two Constant Modulus Equalizers[J].IEEE Communications Letters,2013,17(5):830-833.
[7]Adem Coskun,Izzet Kale.All-Adaptive blind matched filtering for the equalization and identification of multipath channels—a practical approach[J].IEEE Transactions on Circuits and Systems-I:Regular Paper,2013,60(1):232-242.
[8]阮秀凯,等.一族新的Bussgang类指数拓展多模盲均衡算法[J].电子与信息学报,2013,35(9):2187-2193.
Ruan Xiu-kai,et al.A novel bussgang category of blind equalization with exponential expanded multi-modulus algorithm[J].Journal of Electronics & Information Technology,2013,35(9):2187-2193.(in Chinese )
[9]李进,等.MIMO通信系统中QAM信号的快速半盲均衡算法研究[J].电子与信息学报,2013,35(1):185-190.
Li Jin,et al.Study of fast semi-blind equalization algorithm for MIMO systems with QAM signal[J].Journal of Electronics & Information Technology,2013,35(1):185-190.(in Chinese )
[10]Jenq-Tay Yuan,Tzu-Chao Lin.Equalization and carrier phase recovery of CMA and MMA in blind adaptive receivers[J].IEEE Transactions on Signal Processing,2010,58(6):3206-3217.
[11]K N Oh,J H Park.Property restoral approach to blind equalization of digital transmission channels[J].IEEE Transactions on Consumer Electronics,1997,43(3):544-549.
[12]L He,M Amin.A dual-mode technique for improved blind equalization for QAM signals[J].IEEE Signal Processing Letters,2003,10(2):29-31.
[13]F C C.De Castro,M C F.De Castro,D S Arantes.Concurrent blind deconvolution for channel equalization[A].IEEE International Conference on Communications[C].Helsinki:IEEE,2001.366-371.
[14]S Chen.Low complexity concurrent constant modulus algorithm and soft decision directed scheme for blind equalization[J].IEE Proceedings Vision,Image & Signal Processing,2003,50(5):312-320.
[15]郭业才,胡苓苓,丁锐.基于量子粒子群优化的正交小波加权多模盲均衡算法[J].物理学报,2012,61(5):054304-1-054304-7.
Guo Ye-Cai,Hu Ling-Ling,Ding Rui.Orthogonal wavelet transform weighted multi-modulus blind equalization algorithm based on quantum particle swarm optimization[J].Acta Physica Sinica,2012,61(5):054304-1-054304-7.(in Chinese )
[16]阮秀凯,等.基于电域反馈神经网络的自适应盲均衡方法[J].光学学报,2013,33(5):05060021-050600212.
Ruan Xiukai,et al.Adaptive blind equalization using electrical recurrent Neural Networks[J].Acta Optica Sinica,2013,33(5):05060021-050600212.(in Chinese )
[17]李进,等.快速QAM信号多模盲均衡算法[J].电子与信息学报,2013,35(2):273-279.
Li Jin,et al.A fast multimodulus blind equalization algorithm for QAM signal[J].Journal of Electronics & Information Technology,2013,35(2):273-279.(in Chinese)
[18]刘祖军,等.一种新的混合信道盲均衡算法[J].电子与信息学报,2009,31(7):1606-1609.
Liu Zu-jun,et al.A novel hybrid blind channel equalization algorithm[J].Journal of Electronics & Information Technology,2009,31(7):1606-1609.(in Chinese )
[19]王彬,葛临东,霍亚娟.适用于高阶QAM信号的多模混合盲均衡算法[J].数据采集与处理,2011,26(1):8-14.
Wang Bin,Ge Lindong,Huo Yajuan.Multi-modulus based hybrid blind equalization algorithm for high-order QAM signals[J].Journal of Data Acquisition & Processing,2011,26(1):8-14.(in Chinese )
[20]肖瑛,董玉华.并联滤波的常数模与判决引导融合盲均衡算法[J].声学学报,2012,37(5):495-500.
XIAO Ying,DONG Yuhua.The fusion blind equalization algorithm based on constant modulus algorithm and decision direction with parallel filter[J].Acta Acustica,2012,37(5):495-500.(in Chinese)
[21]Ning Xie,Hengyun Hua,Hui Wanga.A new hybrid blind equalization algorithm with steady-state performance analysis[J].Digital Signal Processing,2012,22(2):233-237.
[22]饶伟,郭业才,汪胜前,等.基于坐标变换的常数模盲均衡新算法[J].电子学报,2011,39(1):7-12.
RAO Wei,GUO Ye-cai,WANG Sheng-qian,et al.New constant modulus algorithm for blind equalization based on coordinate transformation[J].Acta Electronica Sinica,2011,39(1):7-12.(in Chinese )
[23]郭业才,等.坐标变换并行软切换盲均衡算法及其DSP实现[J].数据采集与处理,2014,29(2):186-190.
GUO Ye-cai,et al.Coordinate transformation parallel soft switching blind equalization algorithm and its DSP implementation[J].Journal of Data Acquisition and Processing,2014,29(2):186-190.(in Chinese)
[24]RAO Wei.Blind equalization algorithm using a coordinate mapping approach for 4-PAM and 16-QAM signals[J].2014,23(CJE-1):124-128.
[25]V Weerackody,S A Kassam,K R Laker.A simple hard-limited adaptive algorithm for blind equalization[J].IEEE Transactions on Circuits and Systems II:Analog and Digital Signal Processing,1992,39(7):482-487.
[26]Microwave Data.Signal Processing Information Base[DB/OL].http://spib.rice.edu/spib,2014-01-20.
[27]Shahzad Amin Sheikh,Pingzhi Fan.Two efficient adaptively varying modulus blind equalizers:AVMA and DM/AVMA[J].Digital Signal Processing,2006,16(6):832-845.
[28]Lin He,Amin M G,Reed C Jr,Malkemes R C.A hybrid adaptive blind equalization algorithm for QAM signals in wireless communications[J].IEEE Transactions on Signal Processing,2004,52(7):2058-2069.
[29]K N Oh,Y O Chin.Modified constant modulus algorithm:blind equalization and carrier phase recovery algorithm[A].Proc.of IEEE International Conference on Communications[C].Seattle:IEEE,1995.498-502.
[30]Junyu Mai,Ali H Sayed.A feedback approach to the steady-state performance of fractionally spaced blind adaptive equalizers[J].IEEE Transactions on Signal Processing,2000,48(1):80-91.

饶伟男,1982年出生,南昌工程学院信息工程学院副教授,复旦大学信息科学与工程学院在读博士研究生,主要从事通信信号处理及应用等方面的研究工作.
E-mail:wrao14@fudan.edu.cn
高惠娟女,1977年出生,硕士研究生,南昌工程学院信息工程学院讲师,主要从事通信信号处理、图像处理等方面的研究工作.
New Blind Equalization Algorithm Based on a Mapping from a Complex Exponential Function
RAO Wei1,2,GAO Hui-juan2,DUAN Mei-yi2,ZHANG Jian-qiu1
(1.SchoolofInformationScienceandTechnology,FudanUniversity,Shanghai200433,China; 2.SchoolofInformationEngineering,NanchangInstituteofTechnology,Nanchang,Jiangxi330099,China)
A new complex exponential function is defined to map the real and imaginary parts of a classic 16-QAM nonconstant modulus signal to the unit circle,respectively.With the relationship between the real and imaginary parts of the new constellation after mapping,a new cost function is built and then a new blind equalization algorithm is proposed.The proposed algorithm can converge the steady-state mean square error (MSE) to zero under a noiseless environment,which is different from the famous constant modulus algorithm (CMA) and some CMA-based improved algorithms.In addition,we provide the theoretical analysis of the proposed algorithm.Simulation results demonstrate that the proposed algorithm has the lower steady-state MSE than CMA and some CMA-based improved algorithms.
blind equalization;constant modulus algorithm;complex exponential cost function
2014-11-05;
2015-03-04;责任编辑:马兰英
国家自然科学基金(No.61401188,No.61171127);江西省科技支撑计划项目(No.2013ZBBE50016);国家(江西省)大学生创新创业训练计划项目(No.201311319029)
TN911.5
A
0372-2112 (2016)05-1009-08
电子学报URL:http://www.ejournal.org.cn10.3969/j.issn.0372-2112.2016.05.001
