矢量网络分析仪测量不确定度评估算法
2016-09-02赵永久周永刚邓宏伟
王 敏,赵永久,周永刚,贺 莹,邓宏伟
(南京航空航天大学雷达成像与微波光子技术教育部重点实验室,江苏南京 210016)
矢量网络分析仪测量不确定度评估算法
王敏,赵永久,周永刚,贺莹,邓宏伟
(南京航空航天大学雷达成像与微波光子技术教育部重点实验室,江苏南京 210016)
虽然目前校准算法已趋成熟,但由于随机误差和剩余系统误差等的存在,矢量网络分析仪(Vector network analyzer,VNA)的测量结果不可避免地会有一定的不准确性.而现有的矢网测量不确定度评估算法中往往只考虑剩余系统误差,忽略了系统线性性能、线缆状态以及测试环境等因素.本文同时考虑了校准后剩余系统误差、系统非线性误差,随机误差及测量环境等因素,建立了整机测量不确定度模型,实现了矢量网络分析仪整机测量不确定度的评估.与现有矢网不确定度评估算法相比,本算法考虑的误差因素更为全面,评估结果更为可靠.利用误差上限传递思想推导出商用VNA散射参数测量不确定度评估公式,并提供了相应的参数获取方案.应用该算法对安捷伦8753ES矢量网络分析仪进行测量不确定度评估,并与安捷伦提供的技术数据进行对比,其结果数据吻合良好.
矢量网络分析仪;误差模型;散射参数;不确定度
andInformationEngineering,NanjingUniversityofAeronauticsandAstronautics,Nanjing,Jiangsu210016,China)
1 引言
矢量网络分析仪是目前微波/射频研究、开发中使用最广泛的测量仪器.虽然现今已有较为成熟的校准处理技术,但在任何的测量过程中,测量结果仍会受到随机误差和剩余系统误差等的影响,从而引起测量结果的不准确,故测量值伴随其对应的测量不确定度,才是完整的量测结果.近年来,对矢量网络分析仪测量不确定度算法的研究成为新的热点,利用不确定度评价测量结果质量已成为微波仪器生产商的共识.
在目前VNA测量不确定度算法的研究中,大多采用传统12项误差模型[1~7].若单独考虑各项误差对总体测量结果的影响,可通过雅可比矩阵求解协方差以确定误差上限[3,4].但这样算法本身复杂度很高,通用性和灵活性欠佳,并会在求解过程中增加不必要的误差量,从而造成评估结果的不准确.Ulrich Stumper提出的误差偏微分法是最为常用的不确定度分析方法,针对不同的校准方法分析了校准件的非理想性对二端口矢网S参数测量结果的影响[5~7].上述算法均局限于理想的系统线性性能、线缆状态以及测试环境,且运算复杂.为此,J.P.Hoffmann的蒙特卡洛仿真方法考虑了随机误差项对测量结果的影响,但抽样操作繁琐,不利于实际应用[8].
本文通过对商用VNA实际测试机理的研究,对传统12项误差模型进行补充和规划,建立的整机测量不确定度模型充分考虑了剩余系统误差、随机误差及非线性误差等因素,使得对VNA测量不确定度评估更为可靠.利用误差上限传递思想推导商用VNA散射参数测量不确定度算法,并提供了完整的参数获取方案,使不确定度评估工作更具实际操作性.最后,通过该算法对安捷伦E5071C矢量网络分析仪的测量不确定度评估结果与安捷伦技术手册提供的技术数据的对比,验证了该算法的可靠性.
2 VNA测量不确定度算法
2.1系统测试机理及误差模型
在现代微波、射频以及毫米波工程实践中,三通道矢量网络分析仪是目前应用最为广泛的测量仪器.文献[1]中详细分析了VNA的仪器内部结构和测试工作机理,图1给出了三通道VNA的简要内部框图.
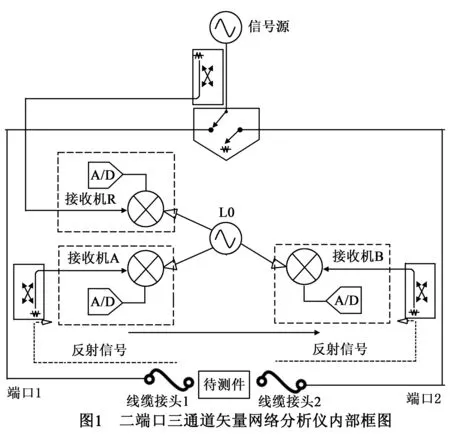
建立一个科学合理且完整的测量系统误差模型是最终获得准确测量不确定度计算结果的根本.校准三通道VNA时,一般采用经典12项误差模型,如图2所示.而在实际测量过程中,尽管可通过校准消除大量误差,大大提高矢量网络分析仪的测量精度,但由于系统误差模型的不精确,校准件的不理想以及人为操作不可重复等因素,校准后系统仍会有部分剩余误差及无法通过校准消除的随机误差残留,导致测量误差.

考虑校准后的剩余系统误差,再引入系统非线性误差和随机误差项,对12项误差模型进行补充和规划,建立如图3所示的32项整机测量不确定度模型.其中包括
(1)系统误差:源端的剩余方向性误差ED、源失配误差ES和反向跟踪误差ER以及负载端的负载失配误差EL和正向跟踪误差ET以及1,2端口之间的串话误差EX.
(2)随机误差:源幅度不稳定度δSR、由线缆弯曲度引起的传输幅度误差δCT和反射幅度误差δCR、由接头重复性引起的传输幅度误差δRT和反射幅度误差δRR以及接收机端的本底噪声NF.
(3)漂移误差:由线缆不理想性引起的相位漂移δCP(图中未标出)以及系统温漂误差DT.
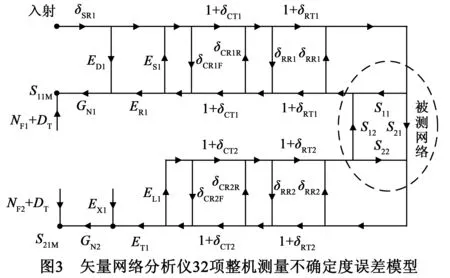
(4)系统非线性误差:接收机线性增益压缩偏差GN.2.2不确定度算法
利用流图化简法可将图3所示的不确定度模型简化成图4所示的简化流图.此过程将原模型的部分不确定度因素合并到新的二端口M网络中.
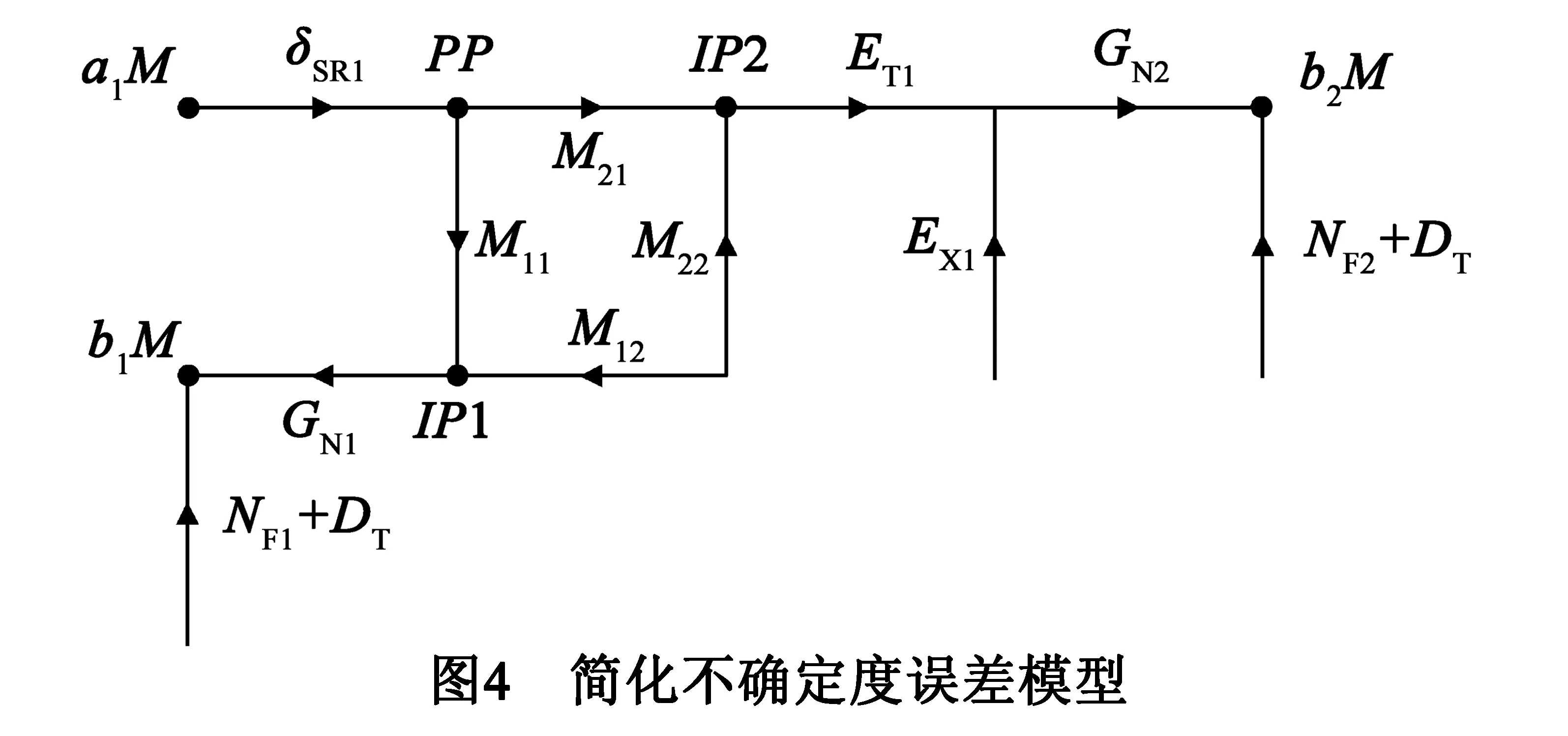
并有,
(1)
(2)
其中,
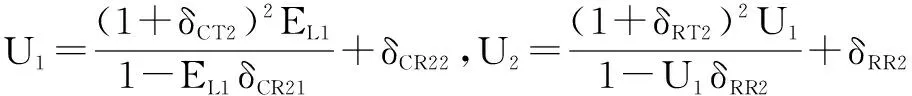
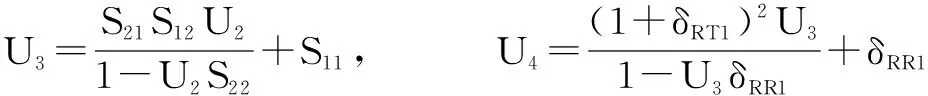
假设1,2端口接收功率RP1、RP2与输入功率IP1、IP2相等,则接收端的实际噪声功率即为:
(3)
其中,NRc为系统本底噪声,PP为用户选定的端口功率.
由图4可以得到二端口待测件的散射参数测量值与真值以及各个误差项之间的数值关系式:
S11M=δSR1×M11×GN1+NF1+DT
(4)
(5)
根据误差传递原理,将不确定度误差模型中各误差项均取其绝对值上限时,最终得到的误差值也必为其误差上限绝对值,即为所求的测量不确定度.
先确定S参数幅度测量不确定度:
US11M=Max{|S11M-S11|}(dB)
US21M=Max{|S21M-S21|}(dB)
(6)
相位测量不确定度可由幅度测量不确定度、被测器件S参数测量值与真值在平面内的关系计算得出.
如图5所示关系,当测量值与真实值达到如图5(b)所示情况时,相位误差最大,此时的α角的大小即为相位测量不确定度.根据图5(b)情况可以计算得
(7)
最终,反射系数相位测量不确定度为:
UPSiiM=α+2δCPi
(8)
传输系数相位测量不确定度为:
UPSjiM=α+δCPi+δCPj
(9)

2.3剩余系统误差参数获取
根据不确定度定义,算法中各误差项参数均为各种可能情况下的误差上限值.商用矢量网络分析仪技术手册可提供部分误差参数的信息,如系统温漂误差和系统非线性误差参数等.为更准确地评估单次测量的不确定度信息,可通过实际测量操作获取各剩余系统误差项参数.
因随机误差不可预示且无法消除,故矢网经校准后,先暂不考虑其影响.
单端口测量时,测量结果仅受剩余系统误差项ED,ES和ER影响,剩余系统误差模型如图6.
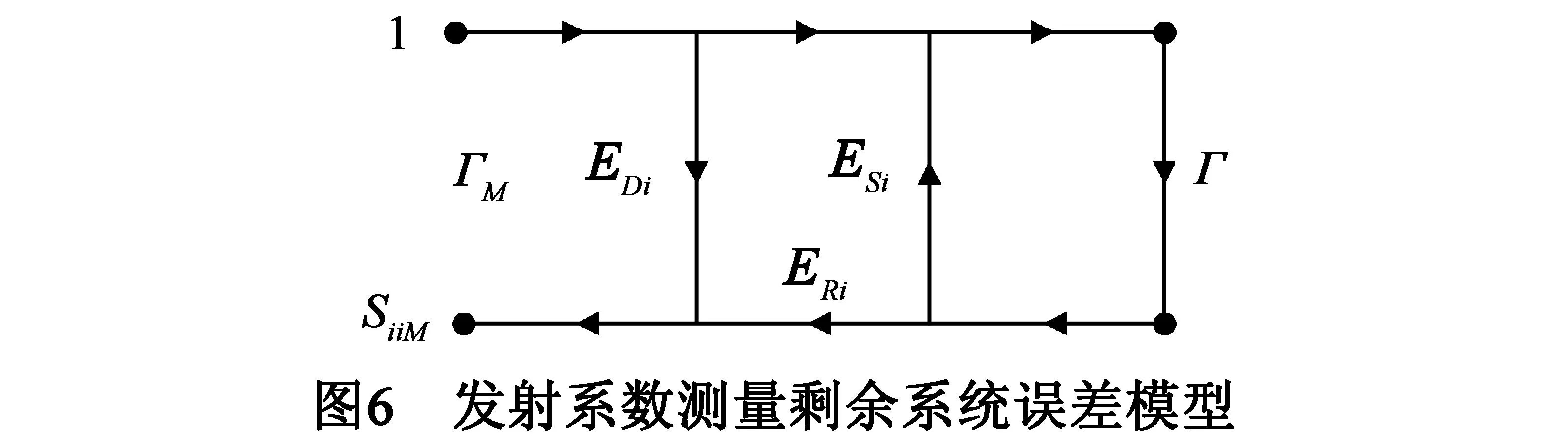
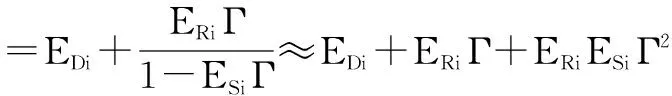
(10)
B.Bianco提出了利用复数交比不变性获取单端口剩余系统误差参数的方法[10].在矢网校准后,分别端接匹配负载、开路及短路标准件,通过测量可得到反射系数真值和偏差值分别为:
端接匹配负载时,Γ1=0,Δ1=ΓL;开路时,Γ2=1,Δ2=ε1;短路时,Γ3=-1,Δ3=ε2;最终可计算得:
EDi=-ΓL
ERi=(ε2-ε1)/2+1
ESi=(ΓL-ε1/2-ε2/2)/ERi
(11)
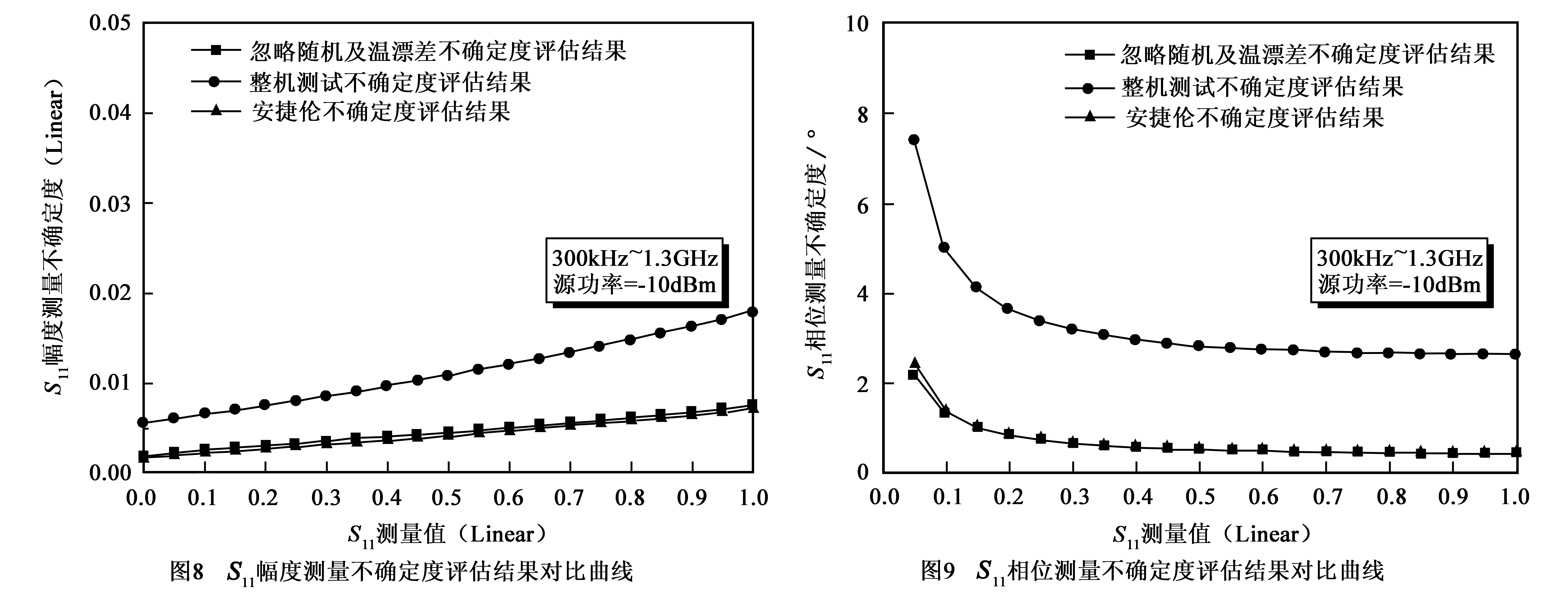
剩余传输跟踪误差、剩余负载失配误差和串话误差可通过传输剩余误差模型确定.由图7可导出:

(12)
从而有
(13)
其中,Δ=S11S22-S21S12.当1、2端口端接匹配负载时,可以直接测得串话误差EXi=Smij(L),i≠j.
ELi做全微分,并忽略二阶及高阶余子式,则剩余负载匹配误差上限的误差函数式为:
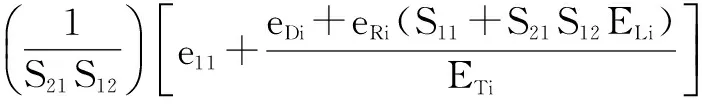
+S21S12ELi2(eSi+e22ETi)+E21ETiS12eLi
(14)
同样可得剩余负载匹配误差上限的误差函数式为:
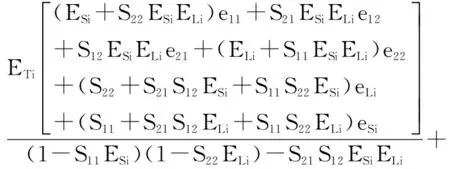
(15)
其中,eDi、eSi、eRi、eTi、eLi、eXi为校准前系统误差,e11、e21、e12、e22分别为S11、S21、S12、S22的测量误差.
可以看出,当1、2端口间为理想直通时,即S11=S22=0,S21=S21=1,此时,ELi≈EDi.而(15)式则简化为:
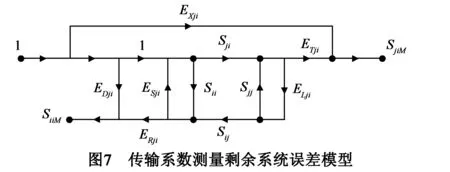
τ=λESi+eSiELi.
2.4算法验证
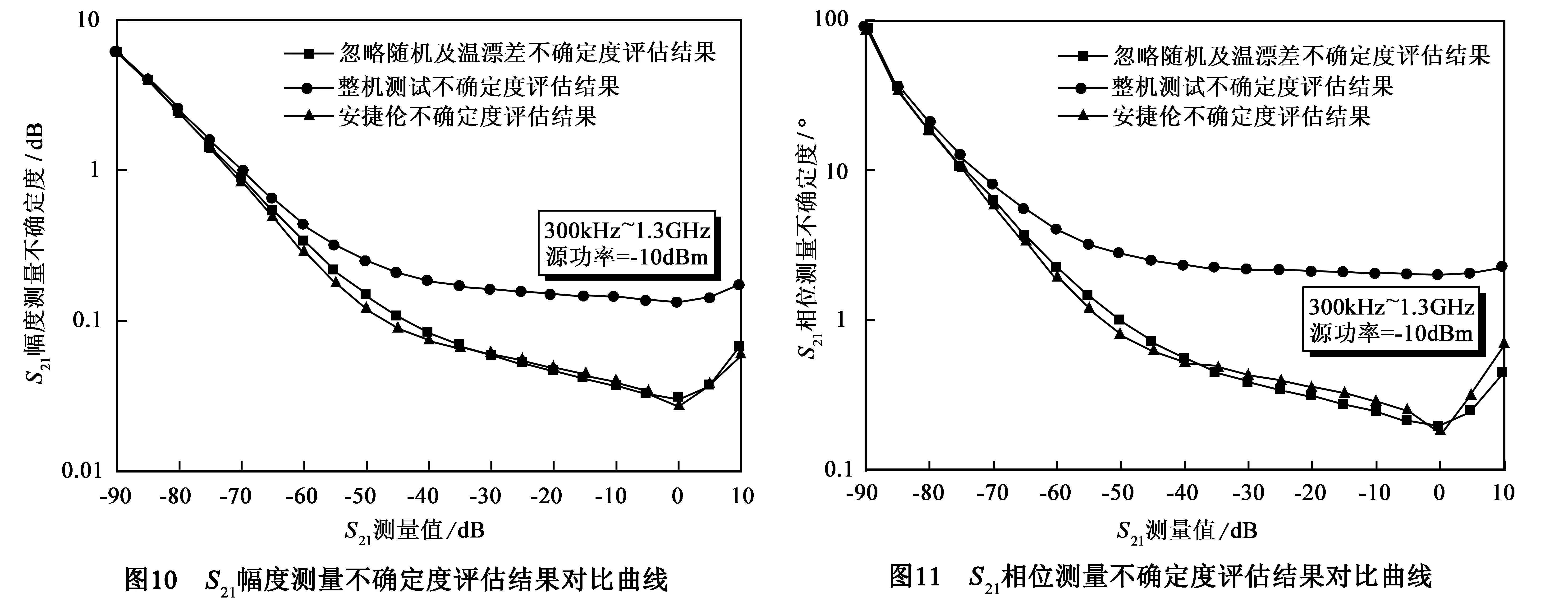
为了验证本算法,选取安捷伦矢量网络分析仪8753ES,利用850313B校准件进行校准.根据技术手册提供的误差参数信息,先忽略线缆、接头引入的随机误差以及系统温漂误差项,即只考虑剩余系统误差与系统非线性误差,利用本文算法对其测量进行不确定度分析;再引入省略误差项,重新评估整机测量不确定度,并与安捷伦技术手册提供的不确定度评估数据进行对比.
图8~11给出了本算法分别只考虑剩余系统误差与系统非线性误差时和整机测量情况下的不确定度评估结果,以及安捷伦评估数据的对比曲线.从图中对比结果可以看出,若忽略线缆、接头引入的随机误差以及系统温漂误差项,本算法的测量不确定度评估结果与安捷伦结果基本吻合,证明了本算法的正确性,而整机测量不确定度评估考虑的误差项更全面,因此评估结果更为可靠.
3 结论
本文通过对商用矢量网络分析仪测量不确定度构成元素及合成机理的分析,建立了更为可靠的整机测量不确定度模型.根据误差上限传输思想推导了不确定度评估算法公式,并提供相应剩余系统误差项参数的获取方案,使该不确定度评估方案更具实际操作性.本文提出算法经实验验证正确可靠.
[1]赵伟.多端口矢量网络分析仪校准技术研究[D].南京航空航天大学,2011.
[2]赵伟,赵永久,秦红波.一种基于10项误差模型的二端口矢量网络分析仪校准方法[J].电子学报,2011,39(10):2469-2472.
Zhao Wei,ZhaoYongjiu,Qin Hongbo.A calibration procedure for two-port vector network analyzer based on 10-term error model[J].Acta Electronica Sinica,2011,39(10):2469-2472.(in Chinese)
[3]张亦弛,齐晓辉,林茂六.基于协方差矩阵的 VNA/NVNA/LSNA 测量不确定度传播规律与分析方法研究[J].仪器仪表学报,2013,33(11):2495-2502.
Zhang Yichi,Qi Xiaohui,Lin Maoliu.Covariance-matrix-based measurement uncertainty propagation law and analysis method for VNA,NVNA and LSNA[J].Chinese Journal of Scientific Instrument,2013,33(11):2495-2502.(in Chinese)
[4]Tong L,Lin M,Zhang Y.Covariance-matrix-based uncertainty propagation analysis for complex-valued quantities throughout VNA S-parameter measurements and power-meter calibration[A].Precision Electromagnetic Measurements (CPEM),2012 Conference on[C].IEEE,2012.106-107.
[5]Stumper U.Influence of nonideal calibration items on S-parameter uncertainties applying the SOLR calibration method[J].Instrumentation and Measurement,IEEE Transactions on,2009,58(4):1158-1163.
[6]Stumper U.Uncertainties of VNA S-parameter measurements applying the TAN self-calibration method[J].Instrumentation and Measurement,IEEE Transactions on,2007,56(2):597-600.
[7]Stumper U.Uncertainty of VNA S-parameter measurement due to non-ideal TMSO or LMSO calibration standards[J].Advances in Radio Science,2003,1(1):1-8.
[8]Hoffmann J P,Leuchtmann P,Schaub J,et al.Computing uncertainties of S-parameters by means of monte carlo simulation[A].ARFTG Conference,2007 69th[C].IEEE,2007.1-7.
[9]Wollensack M,Hoffmann J,et al.VNA Tools II:S-parameter uncertainty calculation[A].Microwave Measurement Conference (ARFTG),2012 79th ARFTG[C].IEEE,2012.1-5.
[10]B.Bianco,A.Corana,S.Ridella,C.Simicich.Evaluation of errors in calibration procedures for measurements of reflection coefficient[J].IEEE Transaction on Instrumentation and Measurement,1978,27(4):354-358.

王敏女,1988年出生于江苏扬中.2011年毕业于南京航空航天大学大学电子信息工程学院电子科学与技术系,2012年考取南京航空航天大学电子信息工程学院电磁场与微波工程系研究生,现在南京航空航天大学电子信息工程学院硕博连读.研究方向为微波电路,微波测量系统.

赵永久(通信作者)男,1964年出生.分别于1990年和1998年获得西安电子科技大学工学硕士和博士学位.博士研究生导师.研究方向为微波电路与子系统、天线理论与技术、现代微波测量技术.
E-mail:yjzhao@nuaa.edu.cn
Measurement Uncertainty Evaluation of Vector Network Analyzer
WANG Min,ZHAO Yong-jiu,ZHOU Yong-gang,HE Ying,DENG Hong-wei
(TheKeyLaboratoryofRadarImagingandMicrowavePhotonics,MinistryofEducation,CollegeofElectronic
Although the VNA calibration theory,at present,has been much mature,measurement uncertainty inevitably exists in practical measurement,due to random errors,linearization and measurement conditions,etc.In the existing VNA measurement uncertainty evaluation algorithms,only residual systematic error is considered,with the ignorance of the influence of system's nonlinearity,random error caused by connector and cable performance and environment conditions.In this paper,four categories of measurement error are taken into account,including residual system error,system's nonlinearity,random error and environment conditions of the measurement.Thus the rational and complete model for uncertainty in measurement is put forward and the uncertainty evaluation method for complete measurement system of VNA is established.Compared with the current VNA measurement uncertainty evaluation algorithms,a more comprehensive consideration of error factors is presented in this algorithm,leading to more reliable assessment results.The formulae of the uncertainty of S-parameter measurement are deduced in term of the theory of error limit transfer,and the corresponding method to get the error parameters is given.The algorithm is applied to measurement uncertainty evaluation for the vector network analyzer Agilent 8573ES and the results are in great agreement with the technical data provided by Agilent.
vector network analyzer;error model;S-parameter;uncertainty
2014-09-29;
2014-12-02;责任编辑:蓝红杰
国家自然科学基金(No.61471193);江苏省普通高校研究生科研创新计划(No.KYLX15-0284)
TM931
A
0372-2112 (2016)05-1085-05
电子学报URL:http://www.ejournal.org.cn10.3969/j.issn.0372-2112.2016.05.011
