可证安全的基于证书广播加密方案
2016-09-02李继国张亦辰卫晓霞
李继国,张亦辰,卫晓霞
(河海大学计算机与信息学院,江苏南京 210098)
可证安全的基于证书广播加密方案
李继国,张亦辰,卫晓霞
(河海大学计算机与信息学院,江苏南京 210098)
广播加密可使发送者选取任意用户集合进行广播加密,只有授权用户才能够解密密文.但是其安全性依赖广播中心产生和颁布群成员的解密密钥.针对这一问题,本文提出基于证书广播加密的概念,给出了基于证书广播加密的形式化定义和安全模型.结合基于证书公钥加密算法的思想,构造了一个高效的基于证书广播加密方案,并证明了方案的安全性.在方案中,用户私钥由用户自己选取,证书由认证中心产生,解密密钥由用户私钥和证书两部分组成,克服了密钥托管的问题.在方案中,广播加密算法中的双线性对运算可以进行预计算,仅在解密时做一次双线性对运算,提高了计算效率.
广播加密;基于证书加密;双线性对
1 引言
对于有N个用户的系统,假设需要通过公开的信道发送某个消息给其中S个用户,要求只有这S个用户能够解密密文,其余用户不能由密文恢复出消息.直观的方法是用这S个用户的公钥分别进行加密,将对应的密文通过公开信道传送,由于这S个用户拥有对应的私钥,可以保证只有指定用户才能进行解密.但这种方法的计算代价很大,消息发送者需要将同一段消息加密S次并传输,而广播加密就可以很好地解决这类问题.广播加密方案是实现一点对多点通信的一种方式,在一个广播加密系统中,广播者可以对某个集合内的用户发起广播,加密后的消息在公开信道上进行传送,任何监听广播的用户均能获得广播密文,只有被授权的合法接收者才可以进行解密,恢复出广播消息,而其它监听广播信道的不法用户均无法恢复广播的明文.在收费电视、数字版权保护、安全电子邮件等特殊领域,其效率远远高于传统的点对点通信方式,有广泛的实际应用背景.
广播加密是一种在不安全信道上给一组用户传输加密信息的密码体制,它可使发送者选取任意用户集合进行广播加密,只有授权用户才能够解密密文.2001年,Naor等人[1]用完备子树和子集差分的方法巧妙地构造了一个高效的广播加密方案,该方案分割集合的效率很高,并使用数学知识证明了两种分割方法的正确性,适用于数量较大的合法用户和数量较少的非法用户集合.Boneh等人[2,3]提出了可抗完全联合攻击的广播加密方案,方案的优点是缩短了密文和密钥的长度,其缺点是公钥长度与接收用户数目成正比.为了克服文献[2,3]中的缺点,Liu等人[4]提出了一个公钥定长的广播加密方案,并缩减了私钥的长度,并证明方案在随机预言模型下可抵抗完全联合攻击.2007年,Delerablée[5]结合基于身份的公钥密码体制提出了基于身份的广播加密方案,方案中密文和私钥长度都是固定的,但是公钥长度与接收用户集合数目成线性关系.Gentry和Waters[6]提出一个半静态安全的新概念,并给出从半静态安全系统到自适应安全系统的通用“双密钥”转换.进一步,构造了具有固定密文长度的广播加密系统.最近,Boneh等[7]使用多线性映射技术较好地解决了公钥广播加密中密文和密钥过长的问题,并给出三个构造.提出的方法能够完全抵抗任意数量合谋者的攻击.上述方案中接收者的解密密钥都是由广播中心计算生成,通过安全通道发送给各个用户,存在密钥托管问题,并且需要建立安全信道.Tan等人[8]提出了一个传统公钥密码体制下的安全公钥广播加密方案,用户的私钥由用户自己选择,避免了密钥托管问题,但是用户私钥由6个群元素组成,公钥由4个群元素组成,用户的密钥存储代价较大,并且存在证书管理问题.Phan等[9]去除了群管理者,提出了分布式动态广播加密的概念,利用“黑盒”思想,给出一个具体的构造,该构造可以看作子集覆盖框架的拓展.伍前红等[10]结合了广播加密和群密钥协商提出了捐助广播加密(ContributoryBroadcastEncryption)密码原语.在这种新密码原语下,提出了具有短密文的捐助广播加密方案.为了解决叛徒跟踪和撤销问题,Hofheinz和Striecks[11]基于文献[12],提出了具有跟踪和撤销的广播加密方案.Boneh和Zhandry[13]使用不可区分混淆技术,构造了多方密钥交换,高效广播加密和叛徒跟踪方案.
Gentry[14]在2003年首次提出基于证书的公钥密码体制(Certificate-BasedCryptography,简称CBC),该体制中用户私钥由用户自己选取,加密方案中的解密密钥由用户私钥和CA颁发的证书构成.由于解密密钥由两部分组成,且证书在公开信道中发送,避免了密钥托管和建立安全信道的问题,也简化了证书的管理,所以基于证书的公钥密码体制为构建安全高效的公钥基础设施PKI(PublicKeyInfrastructure,简称PKI)提供了有效的方法.2006年,Morillo等人[15]基于Waters[16]IBE(Identity-BasedEncryption,简称IBE)方案提出了第一个标准模型下满足自适应选择密文安全的CBE(Certificate-BasedEncryption,简称CBE)方案.Dodis等人[17]利用选择密文安全的IBE方案和PKE(PublicKeyEncryption,简称PKE)方案以及一次签名构造出选择密文安全的CBE方案.为了减少通信代价,Galindo等人[18]对文献[17]中的CBE方案进一步改进,缩短了密文的长度,使其安全规约更加简洁,并在标准模型下证明了方案是自适应选择密文安全的.Lu等人[19]提出高效的基于证书加密方案,该方案通过预计算减少了双线性对的运算次数,仅在解密时做一次双线性对运算,与其它方案相比提高了计算效率.
本文集成基于证书公钥密码体制[14,20,21]的思想,首次提出基于证书广播加密的概念,给出方案的形式化定义和安全模型,构造了一个具体的基于证书广播加密方案,并证明方案在自适应选择密文攻击下是安全的.提出的广播加密方案中用户的私钥为两个群元素,用户的公钥也由两个群元素组成,用户的密钥存储代价较低.在方案中,广播加密算法中的双线性对运算可以进行预计算,仅在解密时做一次双线性对运算,计算效率较高.并且广播系统中的用户可以随时加入或退出广播系统,而不需要对其它用户的密钥进行更新.此外,本文提出的方案可以抵抗完全联合攻击.
2 困难问题假设
定义1双线性映射G1和G2是两个q阶加法循环群,GT是q阶乘法循环群,q为大素数.P1和P2分别是群G1、G2的两个生成元,双线性映射e:G1×G2→GT具备以下三个性质[17,18]:
(1)双线性:对任意的P∈G1,Q∈G2,a,b∈Zq,有e(aP,bQ)=e(P,Q)ab.
(2)非退化性:e(P1,P2)≠1(GT中单位元).
(3)可计算性:e是可有效计算的.
若G1和G2相同,该双线性映射被称为对称双线性映射,G1和G2不同则称为非对称双线性映射.本文使用的双线性映射为对称双线性映射.
定理1如果p=2q+1,且p和q为两个大的奇素数,对于整数a,若0 k-mBDHI困难问题假设如果不存在概率多项式时间算法A能以不可忽略的优势解决G1上的k-mBDHI问题,则称群G1上的k-mBDHI问题是难解的. DDH困难问题假设若不存在概率多项式时间算法能以不可忽略的优势判断T是否等于gab,则称DDH问题在有限域中是难解的. 结合基于证书加密方案的形式化定义和广播加密的一般构造,下面分别给出基于证书广播加密方案的形式化定义及安全模型. 3.1基于证书广播加密的形式化定义 设SN为所有广播用户的集合,其中N={1,2,…,n}.一个基于证书的广播加密方案由一个广播密钥封装机制和一个对称加密方案组成,包括下面五个算法: 系统参数设置算法Setup该算法由CA运行.CA选择系统的安全参数ζ,运行此算法产生主公钥和主密钥(mpk,msk)以及其它系统参数,公开系统参数params(包括系统主公钥mpk),CA保存系统主密钥msk. 用户密钥生成算法Extract该算法由用户IDi(i∈N)运行.用户IDi利用系统参数params生成自己的公/私钥对(PKi,SKi),私钥SKi自己保存,公钥PKi公开. 证书产生算法Certify该算法由CA中心运行.CA以用户IDi的身份信息、公钥PKi、系统参数params和主私钥msk为输入,产生用户证书CertIDi,τ,并通过公开信道发送给用户IDi. 加密算法Enc该算法由广播者运行.广播者选择广播集合S={ID1,ID2,…,IDw},满足w≤n.对于需要广播的消息m,算法以广播集合S、广播公钥PKS和系统公开参数params为输入,先计算(Hdr,k)=Enc(S,PKS),其中报头Hdr是对对称密钥k的封装,k∈K,K为对称加密方案(E,D)的密钥空间,再用对称加密算法E以k为密钥对m进行加密,生成对应的密文C0=Ek(m),将C=(S,Hdr,C0)通过广播信道进行广播. 解密算法Dec该算法由用户IDi(IDi∈S)运行.在收到广播密文C后,用户IDi首先利用私钥SKi、证书CertIDi,τ以及报头信息Hdr恢复出对称加密算法的密钥k=Dec(Hdr,SKi,CertIDi,τ),最后以k和对称加密方案的解密算法D恢复出对应的消息m=Dk(C0)或者直接输出无效标志⊥. 一个安全的基于证书广播加密方案必需满足以下性质: (1)正确性按照方案的步骤正常运行生成的广播密文可以被合法用户正确解密. (2)保密性在不知道合法用户的私钥和证书的情况下,任何监听广播的用户都无法正确解密. (3)抗联合攻击若广播集合外的所有用户联合起来也无法破解广播密文,则称该方案可抵抗完全联合攻击. (4)用户的动态加入和退出可以方便的实现用户加入和退出广播集合,并且对于新加入的用户而言,只能正常解密加入后的广播消息,而不能解密之前的广播消息,对于已撤销的用户而言,不能对撤销之后的广播消息进行解密. 3.2基于证书广播加密的安全模型 2005年,Boneh等人[2]定义了广播加密的静态安全模型.2007年,Delerablée[5]结合基于身份公钥加密的性质,给出了基于身份广播加密方案的安全模型.本文结合上述两个安全模型以及Gentry[14]提出的基于证书加密方案的安全模型,引入公钥替换攻击思想[23~26],首次刻画了基于证书广播加密方案的安全模型.在本文所定义的安全模型下,基于证书广播加密方案的安全性是指在自适应选择密文攻击下,对于静态敌手而言是密文不可区分的,且能抵抗完全联合攻击. 基于证书广播加密方案中包含两类攻击者AI和AII.AI模拟了未认证的用户这一类敌手,它可以获得任意用户的私钥,不可以获得目标广播集合内任何用户的证书,但可以询问目标广播集合外任意用户的证书,可以进行除目标密文外的解密询问,AI还可以进行公钥替换攻击,可以获得替换后公钥所对应的证书,但若敌手AI对目标广播集合内的用户进行了公钥替换攻击,则AI不能询问替换后公钥所对应的证书.AII模拟了一个恶意的CA,它拥有系统主密钥,可以生成任意用户的证书,不可以询问目标广播集合内用户的私钥,但可以获得目标广播集合外任意用户的私钥,AII也可以进行公钥替换,但不可以替换目标广播集合内用户的公钥,可以进行除目标广播密文外的解密询问. 广播加密方案一般是由一个密钥封装算法和一个对称加密算法组成,对称加密算法都是选取自适应选择密文攻击下安全的算法,在定义方案的安全模型时只对密钥封装算法部分进行定义.由于我们的安全模型是针对静态敌手,所以敌手在系统参数生成前需要确定目标广播集合.结合上述两类敌手及其各自不同的攻击能力,下面分别给出两类敌手与挑战者之间的游戏: 游戏1 初始化阶段AI选择目标广播集合S*,S*⊆SN. 系统参数设置挑战者C运行算法Setup,生成系统的主公/私钥对(mpk,msk)以及其它系统参数,C保存主私钥msk,把系统参数params(包括主公钥mpk)发送给AI. 第一阶段询问(Phase 1)在该阶段,AI可向挑战者C自适应地进行下列询问: 公钥询问AI提交任意用户IDi的身份信息,C返回IDi所对应的公钥信息. 私钥提取询问AI提交用户IDi的身份信息,C返回IDi所对应的私钥. 公钥替换AI提交(IDi,PKi′,SKi′),C将IDi的公钥替换为PKi′. 证书询问AI提交(IDi,PKi),若IDi∈S*,C拒绝回复询问;否则C运行证书生成算法,返回(IDi,PKi)对应的证书. 解密询问AI提交(IDi,Si,Hdri),其中IDi∈Si.C运行解密算法返回对应的ki或无效标志⊥. 挑战阶段AI判断Phase1询问结束后,C运行广播加密算法,计算(Hdr*,k*)=Enc(S*,PKS*),k*∈K,然后C随机选择λ∈{0,1},k∈K,令kλ=k*,k1-λ=k,将(Hdr*,k1-λ,kλ)返回给AI. 第二阶段询问(Phase2):AI可继续类似Phase1中的步骤进行询问,但解密询问时不可对Hdr*进行询问. 猜测Phase2询问结束后AI输出λ′,若λ′=λ,则称AI赢得该游戏. 我们定义AI赢得游戏1的优势为: 游戏2 初始化阶段AII选择目标广播集合S*,S*⊆SN. 系统参数设置挑战者C运行算法Setup,生成系统的主公/私钥对(mpk,msk)以及其它系统参数,将主私钥msk和系统参数params(包括系统主公钥mpk)都发送给敌手AII. 第一阶段询问(Phase 1)在该阶段,AII可以自适应地向挑战者C进行下列询问: 公钥询问AII提交任意用户IDi的身份信息,C返回IDi对应的公钥信息. 私钥提取询问AII提交用户IDi的身份信息,若IDi∈S*,C拒绝回复询问;否则返回用户IDi所对应的私钥. 公钥替换AII提交(IDi,PKi′,SKi′),若IDi∈S*,C拒绝替换;否则C将IDi的公钥替换为PKi′. 解密询问AII提交(IDi,Si,Hdri),其中IDi∈Si,C运行解密算法返回对应的ki或无效标志⊥. 挑战阶段AII判断Phase1询问结束后,C运行广播加密算法,生成(Hdr*,k*)=Enc(S*,PKS*),k*∈K,随机选择λ∈{0,1},k∈K,令kλ=k*,k1-λ=k,将(Hdr*,k1-λ,kλ)返回给AII. 第二阶段询问(Phase 2)AII可类似Phase1中的步骤继续进行询问,但解密询问时不可对目标Hdr*进行询问. 猜测Phase2询问结束后AII输出λ′,若λ′=λ,则称AII赢得该游戏. 我们定义AII赢得游戏2的优势为: 注:敌手在进行询问时,允许敌手询问目标广播集合以外的所有用户信息,因此本文给出的安全模型是可以抵抗完全联合攻击的. 在这部分中,首次提出了一个基于证书广播加密方案,并对它进行正确性分析.该方案由以下五个算法组成: 加密算法Enc该算法由广播者运行.广播加密算法由一个密钥封装算法和一个安全的对称加密算法共同来实现: 步骤1广播者选择需要广播的集合S⊆SN. 步骤2对于IDi∈S,广播者依次计算hi=H1(τ‖IDi‖PKi),QIDi∈S=hiP+Q. 步骤4广播者通过公开的广播信道广播消息C=(Hdr,S,C0). 解密算法Dec该算法由用户IDi(IDi∈S)运行.在收到广播密文C后,用户IDi以其私钥SKi、证书CertIDi,τ为输入,按照下面的步骤计算,最后输出C对应的消息m或者无效标志⊥: 步骤4验证H3(σ′,k′)是否等于H3(σ,k),若相等,则以对称加密方案中的解密算法D返回m=Dk′(C0),否则返回⊥. 对于广播的消息该方案只需要进行一次加密,系统可以对g1=e(P,P)进行预计算,加密算法中就不需要进行双线性对运算,仅在解密算法中做一次双线性对运算,提高了计算效率. 正确性分析 本文的方案里,广播集合里的合法用户可将接收到的正确的广播密文恢复出对应的广播消息. (1)用户IDi∈S收到广播密文后计算: 下面根据3.2节提出的安全模型给出本方案的安全性证明.由于不同的敌手具备不同的能力,本文刻画了两个游戏来模拟不同敌手与挑战者之间的交互,从而证明方案的安全性.本文提出的方案是由一个密钥封装算法和一个安全的对称加密算法构成,假定选取的对称加密算法为自适应选择密文安全的算法,在进行安全性证明时,只对密钥封装算法部分进行分析,分析敌手是否能由头文件Hdr以不可忽略的优势区分出对称加密算法的对称密钥k.由于是静态敌手,所以在系统参数产生之前两类敌手都需要先选定目标广播集合. 定理2如果存在概率多项式时间静态敌手AI,经过最多qPK次公钥询问、qSK次私钥询问、qr次公钥替换询问、qH1次H1询问、qH2次H2询问、qC次证书询问、qd次解密询问后,在最多t时间内以不小于ε的概率赢得游戏1,那么就存在一个算法可以在t′时间内以不小于ε′的概率解决k-mBDHI问题,其中k≥(qH1-w),ε′=(1-w/qt)qdε/qH2,w为广播集合内的用户个数,qt=(qPK+qSK+qr+qC+qd). 初始化阶段AI选择目标广播集合S*⊆SN,|S*|=w. 系统参数设置算法(Setup)B运行算法Setup.B令系统主公钥Q=sP,其中sP为k-mBDHI困难问题的输入,主私钥为s未知.将系统参数params={ζ,G1,G2,e,q,P,Q,g1,g2,p,SN,pi,K,H1,H2,H3}发送给AI. 第一阶段询问(Phase 1)B保存列表LAI:{IDi,PKi,SKi,hi,CertIDi,τ,δ},列表初始化为{⊥,⊥,⊥,⊥,⊥,0},列表LH2:{(gi,σi),ki},初始化为{(⊥,⊥),⊥}.在该阶段,AI可以向B自适应地进行下列询问: 公钥询问AI提交任意用户IDi的身份信息,B检查LAI: (2)若IDi不为⊥,B直接返回IDi的公钥PKi. 私钥提取询问AI提交用户IDi的身份信息,B检查LAI. (2)若IDi不为⊥,B直接返回IDi的私钥SKi. 公钥替换AI提交(IDi,PKi′,SKi′),B直接更新列表LAI为:{IDi,PKi′,SKi′,⊥,⊥,1}. H1询问AI提交用户的身份信息IDi和公钥信息PKi,B检查LAI: (1)若IDi∉S*,B随机选择hi,满足hi∈(h1,h2,…,hk)且未曾出现过,更新列表LAI为:{IDi,PKi,SKi,hi,⊥,δ},δ表示保持原状.B返回hi. H2询问AI提交(gi,σi),B检查LH2: (1)若存在{(gi,σi),ki}元组,则B返回ki. (2)若不存在{(gi,σi),ki}元组,B随机选择ki∈K且未曾出现过,将{(gi,σi),ki}添加到LH2中,返回ki. 证书询问AI提交用户IDi的身份信息,若IDi∈S*,B输出⊥并退出(对目标集合中用户公钥询问证书,拒绝询问),否则若IDi∉S*则检查LAI,CertIDi,τ不为⊥时,直接返回CertIDi,τ,否则: 解密询问AI对(IDi,Si,Hdri)进行询问,其中IDi∈Si.若IDi∈S*,则B失败并退出;否则B按步骤计算生成(SKi,CertIDi,τ),运行解密算法: =e(P,P)ri 挑战阶段AI判断Phase1询问结束后,B运行广播加密算法: 第二阶段询问(Phase 2)AI可继续进行Phase1中的各种询问,但解密询问时不可对(IDi,S*,Hdr*)进行询问,其中IDi∈S*. 猜测Phase2询问结束后AI猜测λ′∈{0,1}.B在LH2中随机选择{(gi,σi),ki},B输出(gi)1/li作为k-mBDHI的解. 分析 下面分析B解决k-mBDHI困难问题的概率: B要解决k-mBDHI困难问题就必须保证在与AI进行交互时没有失败退出.由游戏模拟过程可知,当AI对目标集合内用户进行解密询问时,B挑战失败.记事件E1表示AI未对目标集合内用户进行解密询问,其概率Pr[E1]=(1-w/qt)qd. 事件E2表示LH2中存在{(g*,σ*),k*},即AI对(g*,σ*)进行过H2询问,则Pr[λ′=λ]=Pr[λ′=λ|E2]Pr[E2]+Pr[λ′=λ|E2]Pr[E2]≥ε,若AI未对(g*,σ*)进行H2询问,而是随机猜测,则Pr[λ′=λ|E2]=1/2,即[E2] ≥[,可知Pr[E2]≥2Pr[λ′=λ]-1=ε. 事件E3表示B选择了满足需要的{(g*,σ*),k*}元组,其概率Pr[E3]≥1/qH2. B要成功破解k-mDBDHI问题必须保证事件E1,E2,E3同时发生,Pr[B Success]≥(1-w/qt)qd·ε·1/qH2=(1-w/qt)qdε/qH2,即若存在概率多项式时间的敌手AI能在t时间内以不可忽略的优势ε赢得游戏1,则必然存在一个概率多项式时间的算法能够以不小于ε′的概率解决k-mBDHI问题,其中ε′=(1-w/qt)qdε/qH2.而由于k-mBDHI困难问题是难解的,所以不存在概率多项式时间的敌手AI能在t时间内以不可忽略的优势赢得游戏1,即该方案能够抵抗第一类敌手攻击. 定理3如果存在概率多项式时间静态敌手AII,经过最多qPK次公钥询问、qSK次私钥询问、qr次公钥替换询问、qd次解密询问后,在最多t时间内以不小于ε的概率赢得游戏2,那么就存在一个算法可以在t′时间内以不小于ε′的概率解决DDH问题,其中ε′=(1-w/qt)qd(1+ε)/2,w为广播集合内的用户个数,qt=(qPK+qSK+qr+qd). 证明(g,ga,gb,T)为一个DDH问题的输入,构造算法B,在游戏中B模拟挑战者与敌手AII进行交互,最后判断T是否等于gab. 初始化阶段AII选择目标广播集合S*⊆SN,|S*|=w. 第一阶段询问(Phase 1)B保存列表LAII:{IDi,PKi,SKi,δ},初始化为{⊥,⊥,⊥,0},AII可以自适应地向挑战者B进行下列询问: 公钥询问AII提交任意用户IDi的身份信息,B检查LAII: (2)若IDi已存在,B直接返回IDi的公钥PKi. 私钥提取询问AII提交用户IDi的身份信息,若IDi∈S*,B拒绝并输出⊥退出,若IDi∉S*,B检查LAII: (2)若IDi已存在,B直接返回IDi的私钥SKi. 公钥替换AII提交(IDi,PKi′,SKi′),若IDi∈S*,B拒绝替换并输出⊥退出,否则B直接更新列表LAI为:{IDi,PKi′,SKi′,1}. 解密询问AII对(IDi,Si,Hdri)进行解密询问,其中IDi∈Si.若IDi∈S*,则B失败并退出;否则,B同时拥有系统主密钥和用户私钥,直接运行解密算法: =σi. (2)根据riQIDi再计算 e(riQIDi,CertIDi,τ)1/xi2 =e(P,P)ri 挑战阶段AII决定Phase 1询问结束后,B运行广播加密算法: (1)对于IDi∈S*,B计算QIDi∈S*=hiP+Q. 第二阶段询问(Phase 2)AII可类似Phase1中的步骤继续进行询问,但解密询问时不可以对(IDi,S*,Hdr*)进行询问,其中IDi∈S*. 猜测Phase2询问结束后猜测λ′∈{0,1},若λ′=λ,则B输出T=gab,否则输出T≠gab. 分析 下面分析B成功破解DDH问题的概率: B要解决DDH困难问题就必须保证在与AII进行交互时没有失败退出.由游戏模拟过程可知,当AII对目标集合内用户进行解密询问时,B挑战失败.记事件E1表示AII未对目标集合内用户进行解密询问,其概率Pr[E1]=(1-w/qt)qd. E2表示在AII未退出游戏、输出猜测后B解决DDH困难问题的概率,则Pr[E2]=Pr[λ′=λ|T=gab]·Pr[T=gab]+Pr[λ′≠λ|T≠gab]·Pr[T≠gab].T=gab时AII能够区分λ′的概率不小于(1/2+ε),即Pr[λ′=λ|T=gab]≥(1/2+ε),T≠gab时AII不能从各种询问中获得有用信息,只能随机猜测λ′,即Pr[λ′=λ|T≠gab]=Pr[λ′≠λ|T≠gab]=1/2,因此B在AII输出猜测后解决DDH困难问题的概率Pr[E2]≥(1/2+ε)·1/2+1/2·1/2=(ε+1)/2. B要成功破解DDH困难问题必须保证事件E1,E2同时发生,即Pr[B Success]=Pr[E1]·Pr[E2]≥(1-w/qt)qd(1+ε)/2. 若存在概率多项式时间的敌手AII能在t时间内以不可忽略的优势ε赢得游戏2,则必然存在一个概率多项式时间的算法能够以不小于ε′的概率解决DDH问题,其中ε′=(1-w/qt)qd(1+ε)/2.而由于DDH问题是难解的,所以不存在概率多项式时间的敌手AII能在t时间内以不可忽略的优势赢得游戏2,即该方案是能抵抗第二类敌手攻击的. 本文构造了一个高效的基于证书广播加密方案,并证明了方案在自适应选择密文攻击下是安全的.在基于证书广播加密方案中,用户的密钥由用户自己选择,而不是由广播中心分发,避免了密钥托管的问题,同时,由于证书通过公开信道发送,也就不需要建立安全信道.对于需要广播的消息,广播发送者只需要进行一次加密.系统可以对双线性对进行预计算,因此在加密过程中就不需要进行双线性对的运算,在解密时只要做一次双线性对运算,提高了计算效率.并且该方案可以实现用户的动态加入和撤销,不需要更新其它用户的密钥信息,新添加的用户只需将公钥信息添加到公钥列表,而撤销的用户只需删除其公钥信息.但本文给出的具体构造中密文长度与广播集合中用户数量呈线性增长,下一步将重点研究密文定长广播加密方案. [1]Naor D,Naor M,Lotspiech J.Revocation and tracing schemes for stateless receiver[A].Advances in Cryptography-CRYPTO 2001[C].LNCS 2139,Berlin:Springer-Verlag,2001.41-62. [2]Boneh D,Gentry C,Waters B.Collusion resistant broadcast encryption with short ciphertexts and private keys[A].Advances in Cryptology-CRYPTO 2005[C].LNCS 3621,Berlin:Springer-Verlag,2005.258-275. [3]Boneh D,Waters B.A fully collusion resistant broadcast,traces,and revokes system[A].Proceedings of the 13th ACM Conference on Computer and Communications Security[C].ACM New York,NY,USA:2006.211-220. [4]Liu Y R,Tzeng W G.Public key broadcast encryption with low number of keys and constant decryption time[A].PKC 2008[C].LNCS 4939,Berlin:Springer-Verlag,2008.380-396. [5]Delerablée C.Identity-based broadcast encryption with constant size ciphertexts and private keys[A].Advances in Cryptology-ASIACRYPT 2007[C].LNCS 4833,Berlin:Springer-Verlag,2007.200-215. [6]Gentry C,Waters B.Adaptive security in broadcast encryption systems (with short ciphertexts)[A].Advances in Cryptology-EUROCRYPT 2009[C].LNCS 5479,Berlin:Springer-Verlag,2009.171-188. [7]Boneh D,Waters B.Zhandry M.Low overhead broadcast encryption from multilinear maps[A].Advances in Cryptology-CRYPTO 2014[C].LNCS 8616,Berlin:Springer-Verlag,2014.206-223. [8]Tan Z W,Liu Z J,Xiao H G.A fully public key tracing and revocation scheme provably secure against adaptive adversary[J].Journal of Software,2005,16(7):1333-1343. [9]Phan D H,Pointcheval D,Strefler M.Decentralized dynamic broadcast encryption[A].Security and Cryptography for Networks[C].LNCS 7485,Berlin:Springer-Verlag,2012.166-183. [10]Wu Q H,Qin B,Zhang L,Ferrer J D,Farràs O.Bridging broadcast encryption and group key agreement[A].Advances in Cryptology-ASIACRYPT 2011[C].LNCS 7073,Berlin:Springer-Verlag,2011.143-160. [11]Hofheinz D,Striecks C.A generic view on trace-and-revoke broadcast encryption schemes[A].Topics in Cryptology-CT-RSA 2014[C].LNCS 8366,Berlin:Springer-Verlag,2014.48-63. [12]Wee H.Threshold and revocation cryptosystems via extractable hash proofs[A].Advances in Cryptology-EUROCRYPT 2011[C].LNCS 6632,Berlin:Springer-Verlag,2011.589-609. [13]Boneh D,Zhandry M.Multiparty key exchange,efficient traitor tracing,and more from indistinguishability obfuscation[A].Advances in Cryptology-CRYPTO 2014[C].LNCS 8616,Berlin:Springer-Verlag,2014.480-499. [14]Gentry C.Certificate-based encryption and the certificate revocation problem[A].Advances in Cryptology-EUROCRYPT 2003[C].LNCS 2656,Berlin:Springer-Verlag,2003.272-293. [15]Morillo P,Ràfols C.Certificate-based encryption without random oracles[DB/OL].Cryptology ePrint Archive,Report 2006/12,2006. [16]Waters B.Efficient identity-based encryption without random oracles[A].Advances in Cryptology-EUROCRYPT 2005[C].LNCS 3494,Berlin:Springer-Verlag,2005.114-127. [17]Dodis Y,Katz J.Chosen-ciphertext security of multiple encryptions[A].TCC 2005[C].LNCS 3378,Berlin:Springer-Verlag,2005.188-209. [18]Galindo D,Morillo P,Ràfols C.Improved certificate-based encryption in the standard model[J].Journal of Systems and Software,2008,81(7):1218-1226. [19]陆阳,李继国,肖军模.一个高效的基于证书的加密方案[J].计算机科学,2009,36(9):28-31. Lu Y,Li J G,Xiao J M.Efficient certificate-based encryption scheme[J].Computer Science,2009,36(9):28-31.(in Chinese ) [20]Li J G,Huang X Y,Hong M X,Zhang Y C.Certificate-based signcryption with enhanced security features[J].Computers and Mathematics with Applications.2012,64(6):1587-1601. [21]Li J G,Wang Z W,Zhang Y C.Provably secure certificate-based signature scheme without pairings[J].Information Sciences,2013,233(6):313-320. [22]Selvi S,Vivek S,Shukla D.Efficient and provable secure certificateless multi-receiver signcryption[A].ProvSec 2008[C].LNCS 5324,Berlin:Springer-Verlag,2008.52-67. [23]Al-Riyami S S,Paterson K G.Certificateless public key cryptography[A].Advances in Cryptology-ASIACRYPT 2003[C].LNCS 2894,Berlin:Springer-Verlag,2003.452-473. [24]Li J G,Huang X Y,Mu Y,Susilo W,Wu Q H.Certificate-based signature:security model and efficient construction[A].Advances in Cryptology-EuroPKI’07[C].LNCS 4582,Berlin:Springer-Verlag,2007.110-125. [25]Li J G,Huang X Y,Mu Y,Susilo W,Wu Q H.Constructions of certificate-based signature secure against key replacement attacks[J].Journal of Computer Security,2010,18(3):421-449. [26]Li J G,Huang X Y,Zhang Y C,Xu L Z.An efficient short certificate-based signature scheme[J].Journal of Systems and Software,2012,85(2):314-322. 李继国(通信作者)男,1970年生于黑龙江富裕,博士,教授,博士生导师,主要研究领域为信息安全、密码学理论与技术、云计算安全等. E-mail:ljg1688@163.com 张亦辰女,1971年生于黑龙江齐齐哈尔,学士,博士研究生,讲师,主要研究领域为密码学理论与技术. A Provably Secure Certificate-Based Broadcast Encryption Scheme LI Ji-guo,ZHANG Yi-chen,WEI Xiao-xia (CollegeofComputerandInformationEngineering,HohaiUniversity,Nanjing,Jiangsu210098,China) Broadcast encryption allows a sender to securely broadcast to any subset of the group members.However,its security heavily depends on broadcast centre to generate and distribute decryption secret keys for group members.In order to solve the above problem,we propose the notion of certificate-based broadcast encryption,describe the formal definition and security model of the certificate-based broadcast encryption.Furthermore,we also provide an efficient certificate-based broadcast encryption scheme.In our scheme,the decryption key includes user’s private key and a certificate,where the private key is chosen by user himself,and the certificate is generated by certification authority.Therefore,our scheme overcomes the key escrow problem.In addition,our scheme is efficient,because it needs only one paring in decryption algorithm and paring operation in encryption algorithm can be pre-computed. broadcast encryption;certificate-based encryption;bilinear paring 2014-07-29; 2014-11-28责任编辑:马兰英 国家自然科学基金(No.61272542);中央高校基本科研项目(No.2013B07014) TP309 A 0372-2112 (2016)05-1101-10 电子学报URL:http://www.ejournal.org.cn10.3969/j.issn.0372-2112.2016.05.013
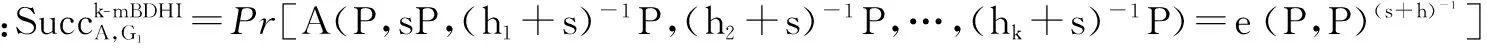
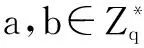
3 基于证书广播加密方案的形式化定义及安全模型
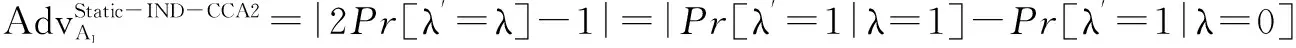
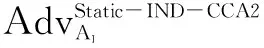
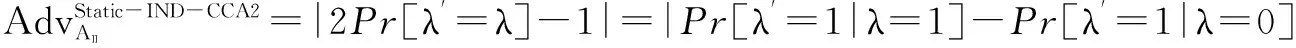
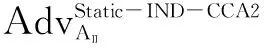
4 基于证书广播加密方案
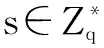

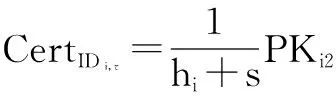
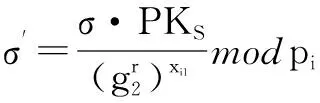

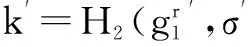

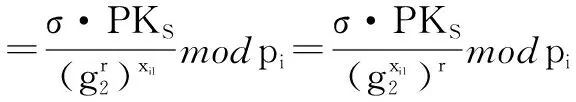

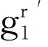

5 安全性证明





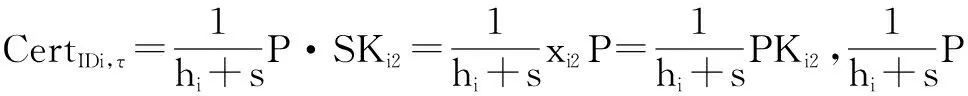
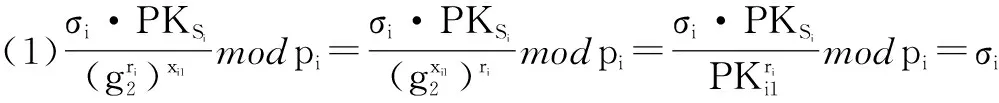

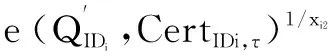
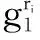

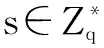
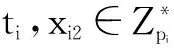

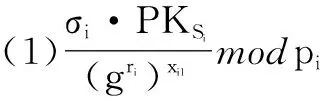
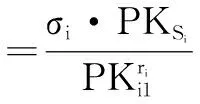
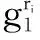
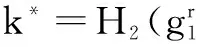

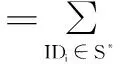
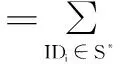
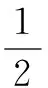
6 结论


