影响复摆周期误差因素的分析研究

许敏明， 王萍

(河池学院　物理与机电工程学院， 广西　宜州　546300)



影响复摆周期误差因素的分析研究

许敏明， 王萍

(河池学院物理与机电工程学院， 广西宜州546300)

针对复摆摆角、空气浮力和复合阻力对复摆周期的影响，分别给出了相应的周期修正公式和周期普遍修正公式，并利用给出的相关公式结合实验实际，定量评估了上述因素对测量复摆周期的影响，分析发现，在大学物理实验中，摆角、空气浮力的影响应该考虑，而复合阻力的影响可忽略不计。

复摆；实验；误差；修正

0　引言

1　复摆实验简介

1.1实验原理

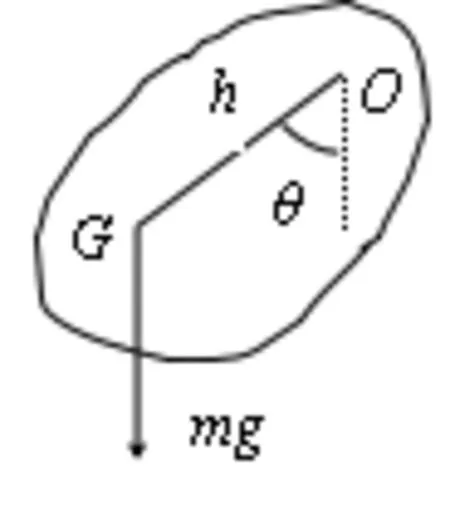
图1　复摆

如图1表示一个形状不规则的刚体，挂于过O点的水平轴(回转轴)上，若刚体离开竖直方向转过θ角度后释放，它在重力力矩的作用下将绕回转轴自由摆动，这就是一个复摆。摆动过程中，复摆受重力和转轴的反作用力，而重力矩起着回复力矩的作用。

设质量为m的刚体绕转轴的转动惯量为I，让刚体绕固定轴O在竖直平面内作左右摆动，G是该物体的质心，质心与轴O的距离为h，θ为其摆动角度。

此时刚体受到一个转动力矩的作用而发生转动，此力矩为

M=-mghsinθ

(1)

其中，θ为转动角位移，负号表示力矩的方向，它总是与角位移方向相反。

根据转动定律，转动力矩M应为刚体转动惯量I与角加速度的乘积，即

(2)

将式(1)的M代入式(2)中稍加整理得

(3)

当转角很小，满足θ<5°时，上式成为

由上式可看出此时刚体的运动是一种谐振动，其振动的圆频率为

(4)

此时复摆的振动周期为

(5)

设a为复摆对质心轴G的回转半径，则刚体对过质心G且平行于回转轴O的转动惯量TG=ma2，根据平行轴定理得

I=ma2+mh2

将此公式代入式(5)，得

(6)

上式即为复摆在无空气阻力、支点光滑无摩擦、摆角无穷小的理想情况下作简谐振动的周期公式，我们把T0称为理想周期，ω0则为理想状态下的圆频率。通过测量复摆在不同支点摆动的周期和回转轴到质心轴的距离h，就可以利用公式(6)近似地算出当地的重力加速度g。

1.2实验仪器装置

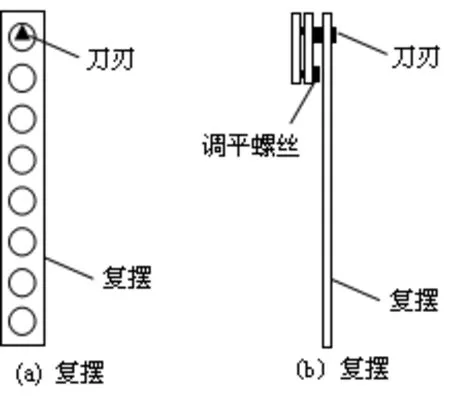
图2　复摆

以如图2所示实验装置为例，实验所用复摆为一均匀钢板，宽约几厘米，长约100厘米。它上面从中心向两端对称地开有数量相同的小孔。测量时分别将复摆通过小圆孔悬挂在固定刀刃上。

常用的计时仪器有数字毫秒计(精度为0.000 1 s)或电子秒表(精度0.01 s)和机械秒表(精度为0.1 s)；测量长度所用的钢尺精度为0.001 m。

2　影响复摆实验误差的因素

2.1影响复摆实验误差因素概述

影响复摆实验误差的因素有系统误差也有随机误差。解决误差问题的重点在于解决系统误差问题，而系统误差的难点在于分析实验方法带来的系统误差，其中包括了实验原理的近似性、实验条件与理论要求的偏差、测量方法等因素，以下重点分析和评估复摆的摆角、浮力以及阻力对实验带来的影响。

2.2复摆周期的理论公式

2.2.1任意摆角的复摆周期公式

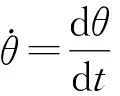
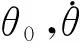
可得出

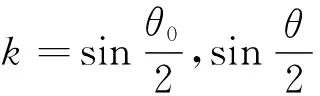
上式是第一类勒让德椭圆积分[1]，其模数为k,按其级数解可求得

略去高次项，得

(7)

由式(7)可看出，考虑摆角影响后的运动周期大于理想周期。

2.2.2在浮力作用下的复摆周期公式

设复摆受浮力为f，则复摆总的转动力矩为

M=(-mgh-fh)sinθ

将上式代入式(2)中稍加整理得

设空气密度为ρ0，复摆密度为ρ，当θ很小时，sinθ≈θ，则上式化为

则周期为

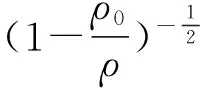
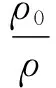
(8)

因此可从式(8)看出引入了浮力之后的周期大于理想周期。

2.2.3在复合阻力作用下的复摆周期公式

在流体中运动的物体受到的阻力比较复杂，一般与物体的截面积、流体的密度成正比，与相对运动速度成正比，影响转轴处摩擦阻力的因素也很复杂，摩擦阻力的大小与转轴的光滑程度及压力状况等有关，摩擦阻力不可能消除。因此复摆在空气中振动时受到的阻力很复杂，与具体复摆的大小、形状、运动状态还有支点状态都有关系[2]。设复摆振动时受到的总阻力fr的大小与复摆的质心速度大小v成正比，阻力的方向都与质心速度方向相反，即

上式中χ是与真实复摆及媒质有关的阻力系数，在通常情况下χ的量级为(10-3～10-2)kg·s-1。则刚体受到的力矩为

将式(2)和式(4)代入上式，复摆的运动方程为

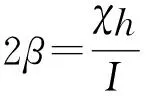
按照微分方程理论，因阻尼较小(β﹤ω0)，由上式可求出复摆的运动方程为

θ=θ0e-βtcos(ωt+φ)

(9)

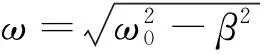
将上式按二项式展开得

上式略去高次项得

(10)

从式(10)可见，复摆在空气中受到复合阻力的周期T大于理想复摆的周期T0.

3　复摆周期普遍修正公式

在任意摆角的复摆周期公式(7)中，如果把空气浮力考虑进去，则式(7)成为

(11)

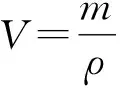
(12)

令

(13)

再考虑复合阻力，这里把式(9)中的ω写为

把复摆的运动周期写为

将式(13)代入上式化简按二项式展开，然后整理、略去高次项得

(14)

即考虑了空气浮力、阻尼、摆角的大小后复摆周期的近似公式为

(15)

4　对影响复摆周期因素的讨论

以下将在普通的大学物理实验条件下对影响复摆周期的因素进行讨论和评估。

4.1角振幅θ0的影响

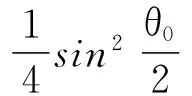
表1　不同角振幅时振动周期的修正量

设复摆的周期为2s，则摆角小于5°时ΔT<0.000 95 s。如果测量时间用的是秒表，精度为0.1 s或0.01 s，则0.01 s比0.000 95(摆角5°时)高2个数量级，若只对周期进行单次测量，则此时由摆角所引起的系统误差可以忽略。如果用的是数字毫秒计时装置，精度为0.000 1 s，此时对复摆周期作单次测量，2°～5°的摆角对周期的影响依然能表现出来，而1°以下的摆角对周期的影响就体现不出来了。

4.2空气浮力的影响

4.3复合阻力的影响

由式(10)知，复合阻力的影响为

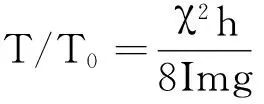
(16)

由式(9)知，复摆作小角振动由于阻力的影响，角振幅随时间的增加按指数方式衰减，规律为

若经过t时间，角振幅从θ0变化到θ1，则阻力系数

把上式代入式(16)得

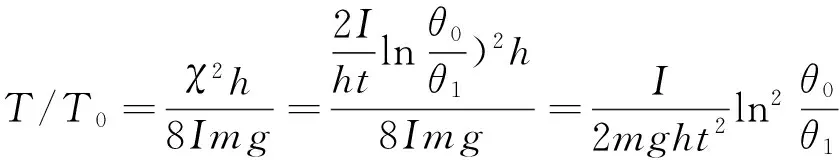
(17)

为算出∆T/T0还必须知道刚体的转动惯量I和角振幅从θ0变化到θ1所用的时间t.

表2　不同支点的复合阻尼修正量

设摆的周期为2 s，从表2知，当悬挂点为第10个时，空气阻尼对复摆周期的影响为∆T/T0=3.04×10-5，则∆T=6.08×10-5s，用数字毫秒计测量得的周期已不能体现出阻尼产生的影响。对比表1和表2的数据可知，其他的悬挂点的阻尼对复摆周期的影响比小摆角和浮力对周期的影响小约2～3个数量级，因此，在实验中一般情况下可忽略不计。而小摆角对复摆周期的影响与空气浮力对周期影响是同一个数量级的，而且其影响能被数字毫秒计时器记录下来，因而在测量精度较高的时候应该对此进行修正，此时，式(15)可简写为

在大学物理实验中，用上式作为复摆的周期公式已能满足较高测量精度的要求。

[1]王梓坤.常用数学公式大全[M].重庆:重庆出版社,1991:465-467.

[2]何松林,黄焱.复合阻力作用下复摆振动的研究[J].西南师范大学学报(自然科学版),2010,35(4):220-223.

[3]何松林,黄焱,戴祖诚．复摆实验修正阻力影响的研究[J].实验室研究与探索,2010,29(7):41-43.

[Abstract]Aiming at the influence of compound pendulum swing angle, air buoyancy and composite resistance on compound pendulum period, this paper puts forward some corresponding periodic correction formula and cycle generally modified formula, and by using the given formula to combine with the experiment practice, carries out a quantitative assessment of the effects of mentioned factors on the measurement of compound pendulum.Analysis found that in college physical experiments, swing angle and air buoyancy’s effects should be taken into account, and impact of composite resistance can be ignored.

[Key words]compound pendulum; experiment; error; correction

[责任编辑刘景平]

Analysis Research on Factors Influencing Compound Pendulum Period Error

XU Min-ming, WANG Ping

(School of Physics and Mechanical & Electronic Engineering, Hechi University,Yizhou, Guangxi 546300, China)

G642；O321

A

1672-9021(2016)02-0111-07

许敏明(1976-)，男，广西宜州人，河池学院物理与机电工程学院讲师，主要研究方向：大学物理、核物理。

广西高校中青年教师基础能力提升项目(KY2016YB385)；河池学院青年科研基金资助项目(XJ2015QN002)；河池学院教学软件资助课题(2015ER07)。

2016-03-01