单峰分布下三段截尾变量期望下界的估计

李 宗 秀

(黑龙江财经学院 基础部 哈尔滨150025)



单峰分布下三段截尾变量期望下界的估计

李 宗 秀

(黑龙江财经学院 基础部 哈尔滨150025)

在假定随机变量X∈[-a,+∞]且为单峰分布的条件下，利用随机变量X若干矩信息，通过对偶理论引入简单变换，最后得出三段线性函数期max(0,X,mX-z)望下界的估计.是三段线性函数期望半参数界的推广，进一步研究了截尾随机变量期望界的问题，为金融经济等研究领域提供了理论依据.

截尾变量；对偶理论；单峰分布；期望

本文的内容属于矩问题中三段线性函数期望的研究，最早追溯到俄国数学家Chebyshev，他的Chebyshev不等式[1]被认为是第一个系统研究矩问题依据，而随机变量函数的期望的半参数界源于Scarf[2]成本控制中的研究，后期，Lo[3]，Grundy[4]，Cox[5]的重要文献也驱动了随机变量函数半参数界的发展.这些研究被广泛应用于收益函数，股票价格和欧式期权中.新加坡学者Natarajan和Zhou[6]于2007年得到三段线性函数的期望Emax(0,S,aS-b)的上界，此结果推广了欧式期权并用最优化的方法得到了完整的结果.单峰分布最早源于Gauss-Winkler不等式[7]，它由Gauss提出的，后来Winkler加以完善.1970 年，多维单峰变量的研究备受关注，Popescue[8]将一维单峰分布的结果推广到多维情形，2007年，双峰分布又得到了广泛的应用[9].在国内，对截尾变量期望的研究有突出贡献的就是李文博教授和刘国庆老师[10]，2010年，张银龙等[11]发表了两类截尾变量的均值与方差的估计一文，对后续的研究起了重要作用.2011至今，刘国庆，李宗秀，吴捷等人对三段截尾变量数字特征上下界的估计也做出了很多的贡献，见参考文献[12-13].

定理 设随机变量X∈[-a,+∞]，且X为单峰分布，众数为Md>0，当随机变量X满足EX=m1，EX2=m2时，三段线性函数H(x)=max(0，x,mx-z),其中m>1,z>0.则

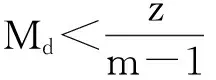
(1)

(2)

证明 1) 构造二次函数Q(y)=ky2+g使其满足Ψ(y)≥Q(x)此二次函数以y=0为对称轴，与Ψ(y)的第一段函数相切于点d.则有 Emax(0,X,mX-z)≥EQ(X)=k(3m2-2m1Md)，当Q(x)满足如下条件

即

解得

(3)

此时

(4)

所以

(5)

令[EQd(X)]′=0，由于d<0，得

(6)

(7)

3) 构造二次函数Q(y)=ky2+g使其满足Ψ(y)≥Q(y)，此二次函数以y=0为对称轴，与Ψ(y)的第一段函数相切于点d则有Emax(0,X,mX-z)≥EQ(Y)=k(3m2-2m1Md)+g ，当Q(x)满足如下条件

(8)

即

解得

此时

(9)

所以

(10)

令[EQd(X)]′=0，由于d<0，得

(11)

将式(11)代入式(10)得

其中

(12)

综上，有

其中

(13)

[1]PRANGERW.Extremepointsofconvexsets[J].Math.Ann., 1973, 205: 299-302.

[2]ARROWKJ,KARLINS,SCARFH.Mathematicaltheoryofinventoryandproduction[M].Stanford:StanfordUniversityPress, 1958.

[3]LOA.Semiparametricupperboundsforoptionpricesandexpectedpayoffs[J].J.Finan.Econom., 1987, 19: 373-388.

[4]GRUNDYB.Optionpricesandtheunderlyingassetsreturndistribution[J].J.Finan., 1991, 46(3): 1045-1069.

[5]COXSH.Boundsonexpectedvaluesofinsurancepaymentsandoptionprices[J].Trans.Soc.Actu., 1991, 43: 231-260.

[6]NATARAJANK,ZHOUYL.Amean-varianceboundforathree-piecelinearfunction[J].ProbabilityintheEngineeringandInformationalSciences, 2007, 21(4): 611-621.

[7]KARLINS,STUDDENW.Chebyshevsystems:withapplicationsinanalysisandstatistics,pureandappliedmathematics[M].NewYork:JohnWileyandSons, 1966.

[8]POPESCUI.AsemidefiniteprogrammingapproachtooptimalmomentboundsforconvexclassesofDistributions[J].Math.Oper.Res., 2005, 30: 632-657.

[9]BLOCKHW,LIY,SAVITTH.Mixturesofnormaldistributions:modalityandfailurerate[J].Stat.Prob.Lett., 2005, 74(3): 253-264.

[10]LIUGQ,LIWV.Momentboundsfortruncatedrandomvariables[J].StatisticsandProbabilityLetters, 2009, 79: 1951-1954.

[11]张银龙, 刘国庆, 王敏慧. 两类截尾变量的均值与方差的估计[J]. 哈尔滨理工大学学报, 2010, 10: 74-77.

[12]李宗秀, 刘国庆. 三段截尾变量概率分布的上界[J]. 高师理科学刊, 2011, 4: 4-6.

[13]李宗秀, 吴捷. 三段截尾变量小值概率上界的估计[J]. 哈尔滨商业大学学报:自然科学版, 2011,27(4): 114-116.

Estimates on lower bounds of mean for three-piece truncated randomvariablesofunimodaldistribution

LI Zong-xiu

(Department of Basic, Heilongjiang Finance and Economy College, Harbin 150025, China)

Thispapersupposedrandomvariablesundertheconditionoftheunimodaldistribution,Introducedthesimpletransformationbasedonthedualtheoryunderseveralmomentconditionsofit.Atlast,gettheestimatesoflowerboundsformeanofatruncatedthree-piecelinearfunctionofthisrandomvariable.Thispaperimprovedthesemiparametricboundsformeanofathree-piecelinearfunctionofarandomvariable,alltheresultsinthispaperastoprovidethetheoryevidenceforfinanceandeconomy.

truncatedvariable;dualtheory;unimodaldistribution;mean

2016-03-20.

黑龙江省教育教改项目(JG2014010930)；黑龙江省教育科学规划课题(GJD1215031)；黑龙江财经学院院级课题(2016YB05)

李宗秀(1980-)，女，硕士，讲师，研究方向：概率论与数理统计.

O211

A

1672-0946(2016)04-0479-03