改进局部均值分解方法及其在往复压缩机轴承故障诊断中的应用
2016-09-01赵海洋王金东邢俊杰
赵海洋,韩 辉,王金东,邢俊杰
(东北石油大学 机械科学与工程学院,黑龙江 大庆 163318)
改进局部均值分解方法及其在往复压缩机轴承故障诊断中的应用
赵海洋,韩辉,王金东,邢俊杰
(东北石油大学 机械科学与工程学院,黑龙江 大庆 163318)
往复压缩机广泛应用于石油、化工生产行业,其滑动轴承常因磨损而出现间隙过大故障。针对往复压缩机振动信号的强非平稳和非线性特性,提出一种改进局部均值分解(LMD)方法,并将其应用于往复压缩机轴承间隙故障诊断。通过在极值点间加入极值对称点,使用单调三次Hermite插值(MPCHI)替代三次样条插值(CSI)构造包络线,提高局部均值与包络估计函数的准确性,以此提出了改进LMD方法的算法与流程。以往复压缩机轴承故障振动信号为对象,通过与不同LMD方法比较,验证改进的LMD方法的优越性,并以PF分量幅值包络频谱实现轴承间隙大故障的准确诊断。
振动与波;往复压缩机;LMD;单调Hermite插值;轴承;故障诊断
往复压缩机因其压力适用范围广和适用性强等特点,已在石油、化工行业广泛应用[1]。传动机构是往复压缩机动力传递以及运动形式转换的重要部件,其连杆与各部件间通常使用滑动轴承连接。运行时间一久,滑动轴承常因磨损而出现间隙过大故障,进而使机体剧烈振动。近些年来,学者开展了大量的轴承故障诊断方法研究。其中,振动信号富含设备状态信息,采集方便,是一种理想的故障状态特征提取信息源[2]。然而,往复压缩机因结构复杂、激励源众多,其振动信号呈强非平稳性、非线性,且故障特征信息耦合于背景噪声之中,经典振动信号故障诊断方法在其故障特征提取过程中存在一定的局限性。
近些年来,信号自适应分解方法已成为故障特征提取领域的新兴研究热点,尤其适合于具有非平稳、非线性特性的信号特征提取。其中,LMD是英国学者Smith提出的一种信号自适应分解方法[3],程军圣等人[4]证明了该方法在降低端点效应、减弱包络不准现象以及保留信息性等方面都比EMD方法具有优势。任达千[5]系统地阐述了LMD的算法和定义,进行了LMD在旋转机械故障特征提取中的应用研究。
局部均值函数和包络估计函数的构造是LMD方法核心步骤,直接关系到分解精度。传统LMD方法所使用的滑动平均法,在多次平滑过程中可能会产生相位误差,从而影响分解精度[4]。受EMD思想启发,浙江大学任达千等人[5]提出了使用三次样条插值(CSI)构造包络线以替代滑动平均法,有效解决了这一问题。但与EMD类似,在包络线构造过程中,因三次样条插值2阶导数连续,包络线在保证光滑性的同时产生了过包络或欠包络现象,且这一现象在强非平稳信号中尤为显著。再者,现有LMD方法仅以信号局部极值点为信息,使用不同插值方法构造包络线,并不能完全反映原始信号的波形特性。因此,进一步挖掘信号初始信息,并提出一种新型包络线构造方法,避免过包络等现象,是增进局部均值函数和包络估计函数准确性进而提高LMD分解精度的一种有效途径。
针对往复压缩机振动信号的强非平稳、非线性特性,提出一种局部均值函数和包络估计函数构造方法,进而提高LMD分解精度。应用改进LMD方法分析往复压缩机振动信号,实现轴承间隙故障的准确诊断。
1 改进LMD方法
1.1单调三次Hermite插值包络(MPCHI)
三次Hermite插值(PCHI)是一种应用广泛的插值算法,其插值曲线形状主要取决于插值点1阶导数。相比于三次样条插值(CSI),既保持了插值曲线的光滑特性,同时又具有优良的保形特性,而且通过合理设置插值点的1阶导数,可以使两点间插值曲线保持单调[6],从而有效避免了CSI方法存在的过包络与欠包络现象,尤其适合于强非平稳信号的包络。
单调三次Hermite插值定义如下:数据(xi,yi,di)中yi与di分别是分划点xi(i=0,…,n)处的函数值和1阶导数值。设hi,∆i,∆yi分别为
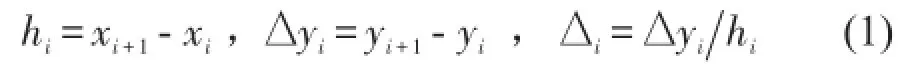
如果数据点是单调的,例如,∆yi≥0∀i或∆yi≤0∀i则
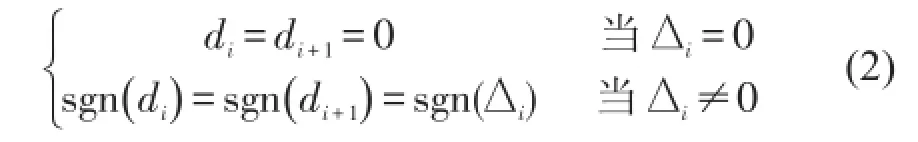
在区间x∈[xi,xi+1]内,对于给定的初始值S(xi)=yi和 S'(xi)=di的单调三次 H ermite插值S(x)∈C1[a, b] 可以定义为
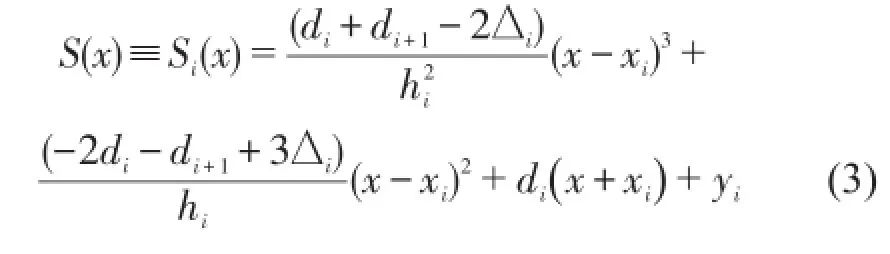
1.2ITD极值对称点
内禀时间尺度分解(ITD)方法是近些年来发展起来的一种新兴的自适应分解方法[7],它能自动将信号分解为一系列旋转分量(PR)。ITD与LMD的差异在于二者使用了不同的基函数构造方法。相比于LMD使用的极值点包络线,ITD是利用基线控制点和线性变换来构造基函数的。
对于确定信号Xt(t≥0)的极值Xk及对应的时刻τk(k=1,2,...M),ITD将其分解为基线Lt与旋转分量Ht之和,即

而在区间(τk,τk+1]内的基线Lt可以通过如下的线性变换得到
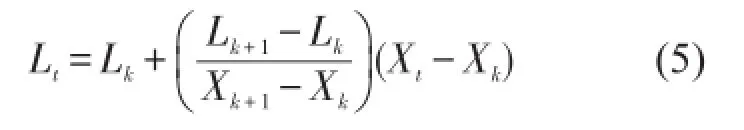
其中
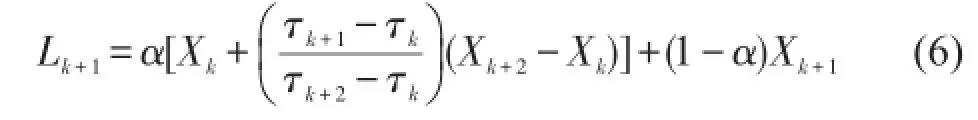
式中α∈(0,1),一般地取α=0.5。
在此定义Ak+1为
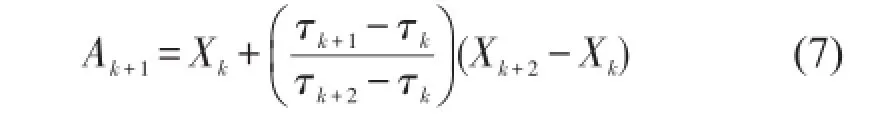
取α=0.5,则公式(6)可表示为
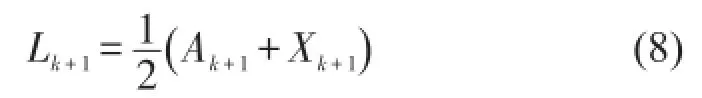
如图1所示,由于Ak+1与极值点Xk+1关于基线控制点Lk+1相互对称,因此,将Ak+1命名为极值对称点。

图1 ITD方法中局部信号基线构造
相比于LMD方法中仅仅依靠极值点Xk构造包络线,ITD利用所特有的极值对称点Ak+1将原始信号中更多的固有信息传递到基线信号中,提高了信号分解精度。因此,借鉴ITD构造基线构造方法,在LMD构造包络线过程中,于相邻两极大(小)值点Xk和Xk+2间插入极值对称点Ak+1,随后再使用MPCHI方法生成包络线,既可避免CSI的过包络与欠包络现象,又可以使原始信号中更多的固有信息传递到了包络线中,是提高LMD局部均值函数与包络估计函数精度的一种有益尝试。
1.3改进LMD算法
在局部均值函数与包络估计函数的上下包络线构造过程中,为避免过包络与欠包络现象,并充分挖掘信号初始信息,于现有极值点间插入极值对称点,并使用MPCHI生成包络线,从而提出一种改进的LMD算法。对于信号x(t),改进LMD算法如下:
(1)设置初始参数:ui(t)=x(t),sij(t)=ui(t),i=0,j=0;
(2)确定信号sij(t)的所有极值序列ni,j,k;
(3)根据式(7)计算所有极值序列ni,j,k所对应的极值对称点序列Ai,j,k;
(4)按照在两相邻的极大(小)值点间插入一个极小(大)值对称点的原则,将极值序列ni,j,k和极值对称点序列Ai,j,k分为最大极值序列n maxi,j,k和最小极值序列n mini,j,k;
(5)根据式(3),分别使用MPCHI计算得出最大极值序列n maxi,j,k所对应的上包络线Euij(t),以及最小极值序列n mini,j,k所对应的下包络线Elij(t);
(6)利用得出的上包络线Euij(t)和下包络线Elij(t)即可计算得出局部均值函数mij(t)与包络估计函数aij(t)分别为
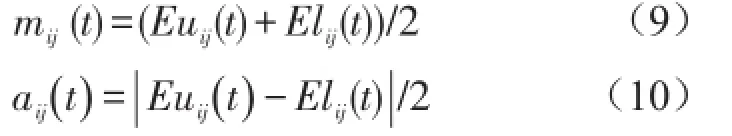
继续执行标准LMD算法的其余步骤,即可将信号x(t)分解为一系列PF分量。改进LMD算法的流程如图2所示。
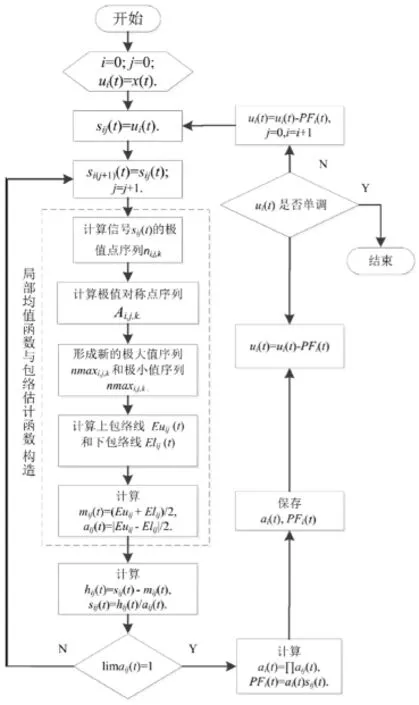
图2 改进LMD方法流程图
2 往复压缩机轴承故障诊断
2D12型往复压缩机是天然气增压输送的常用设备,其电机转速为496 r/min,排气量为70 m3/min,活塞行程为240 mm。故障实验过程中,在压缩机传动机构的一级连杆大头轴承处,利用已磨损的轴瓦,模拟轴承间隙过大故障。经振动传递机理分析,选择曲轴箱旁的十字头滑履下端作为测点,采用加速度型振动传感器、信号放大器和数据采集仪记录故障状态信号。实测信号时域波形如图3所示。
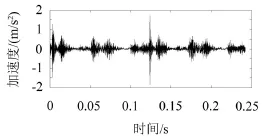
图3 往复压缩机轴承故障状态振动信号
由图3可知,振动信号出现了强烈非平稳的冲击现象,这是因为轴承间隙过大时,轴与轴瓦剧烈碰撞所致。
往复压缩机内部运动部件众多,机体实测振动信号可视为多个内部激励源对机体固有振动频率调制叠加而成,且内部激励多具有时变性。因此,机体振动信号属于强非平稳多分量耦合信号,而LMD方法既能自适应解耦,又适用于非平稳信号,是其理想的分析方法。
为了评价改进LMD方法对强非平稳信号的适应性,应用改进LMD、CSILMD和标准LMD方法对故障信号进行分析。鉴于设备状态信息主要集中于LMD分解结果的前几个PF分量,在此,仅给出分解结果中的前三个PF分量。改进LMD、标准LMD和CSI LMD方法的分解结果分别如图4至图6所示。通过对比可知,CSI LMD方法的PF3分量因过包络与欠包络现象而出现了幅值突变。
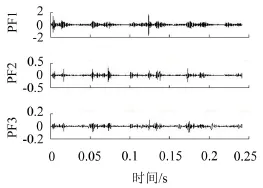
图4 改进LMD振动信号分解结果

图5 标准LMD振动信号分解结果
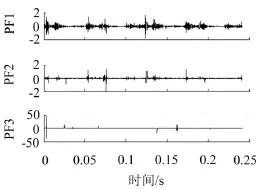
图6 CSI LMD振动信号分解结果
为了定量评价不同方法的分解性能,采用如下指标进行比较:各个PF分量的迭代次数、均值正交指标(Average for Index of Orthogonality,IOave)以及能 量 守 恒 指 标(Index of Energy Conservation,IEC)[8-9]。通常,包络线的拟合越精确,达到迭代终止标准所需包络解调的次数越少,因此,PF分量迭代次数越少说明包络方法精度越高。再者,分解结果中各PF分量理论上应是完全正交的,即正交指标IO=0,但是由于误差的存在,正交性只是相对的,可以正交指标作为分解结果的定量评价标准。在此,具体以正交性均值IOave作为评价标准。此外,信号分解前后应该满足能量守恒定律,若PF分量完全正交,则能量守恒指标IEC=1,从能量角度该指标也可对结果进行评价。IOave与IEC定义如下
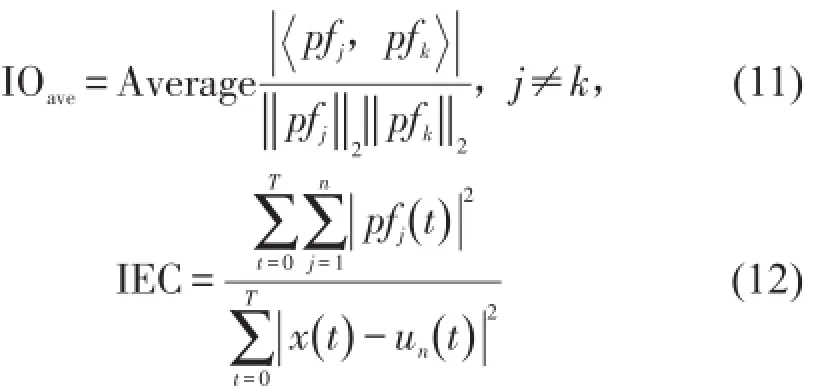
式中x(t)为原始信号,pfj(t)为各个PF分量,un(t)为残余分量。
三种方法前三个PF分量的迭代次数、均值正交指标以及能量守恒指标如表1所示。由表1可知,因CSI LMD方法出现过包络现象,其迭代次数较多,而改进LMD又明显优于标准LMD法,迭代次数最少。在正交性和能量守恒指标方面,改进LMD方法均明显优于其它两种方法,进一步验证了MPCHI插值法对压缩机振动信号的优良拟合逼近性能以及选择极值对称点作为包络线控制的有效性。

表1 不同LMD方法分解结果对比
往复压缩机振动信号中,幅值调制频率是内部激励频率的真实反映。因此,通过对振动信号的包络幅值进行频谱分析可更直观地反映设备的运行状态。首先,对原始信号进行包络频谱分析,结果如图7所示。
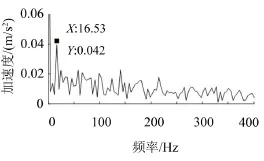
图7 故障状态振动信号包络谱
由图7可知,在16.3 Hz即二倍频处出现了峰值。轴承正常间隙状态时,轴与轴瓦通过油膜连续接触,碰撞激励较小。而间隙增大后,轴与轴瓦在一个往复周期内产生两次分离撞击过程,因此,其故障特征频率为二倍频。随后对PF1分量的瞬时幅值a1(t)进行频谱分析,结果如图8所示,同样出现了二倍频的故障特征频率。但通过对比可知,图7中虽然出现了二倍频的故障特征频率,但相对比于其它频率成分并不十分显著,不利于故障状态的准确判定,而图8在二倍频处幅值十分显著,明显高于其它频率成分,可以准确判定故障状态。对比结果说明原始信号经LMD分解后故障信息更突出了,更能准确地诊断出往复压缩机轴承间隙过大故障。
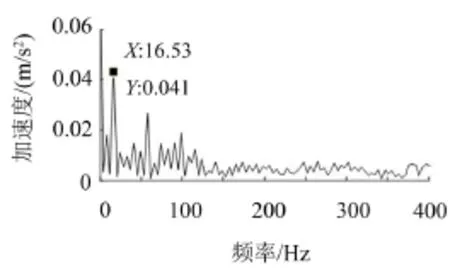
图8 PF1分量瞬时幅值频谱
3 结语
针对往复压缩机振动信号的强非平稳、非线性特性,给出一种局部均值函数和包络估计函数构造方法,进而提出一种改进LMD方法。
(1)提出了通过在极值点间加入极值对称点,使用MPCHI替代CSI的局部均值函数与包络估计函数构造方法,以此改进了LMD方法的算法与流程。
(2)以往复压缩机轴承故障振动信号为对象,通过与不同LMD方法比较,使用PF分量迭代次数、均值正交指标以及能量守恒指标验证改进LMD方法的优越性。
(3)以PF分量幅值包络频谱中特征频率为依据,准确诊断轴承间隙过大故障,进一步验证了改进LMD方法对往复压缩机强非平稳特性振动信号的适用性。
[1]赵海洋,徐敏强,王金东.基于多重分形与奇异值分解的往复压缩机故障特征提取方法研究[J].振动与冲击,2013,32(23):110-114.
[2]邹龙庆,陈桂娟,邢俊杰,等.基于LMD样本熵与SVM的往复压缩机故障诊断方法[J].噪声与振动控制,2014,34(6):174-177.
[3]JONATHAN S SMITH.The local mean decomposition and its application to EEG perception data[J].Journal of the Royal Society Interface,2005,2(5):443-454.
[4]张亢,程军圣,杨宇.基于有理样条函数的局部均值分解方法及其应用[J].振动工程学报,2011,24(1):97-103.
[5]胡劲松,杨世锡,任达千.基于样条的振动信号局域均值分解方法[J].数据采集与处理,2009,24(1):82-86.
[6]张宝琳.逐段单调三次样条插值[J].数值计算与计算机应用,1983(3):157-162.
[7]FREI M G,LVAN O.Intrinsic time-scale decomposition: Time frequwncy energy analysis and real-time filtering of non-stationary signal[C].Proceedings of the Royal Society A:Mathematical,Physical and Engineering Science,2007,463:321-342.
[8]张亢,程军圣,杨宇.局部均值分解方法中乘积函数判据问题研究[J].振动与冲击,2011,30(9):84-89.
[9]王明达,张来斌,梁伟,基于B样条插值的局部均值分解方法研究[J].振动与冲击,2010,29(1):73-78.
Improved Local Mean Decomposition Method and Its Application to Fault Diagnosis of Reciprocating Compressor Bearings
ZHAO Hai-yang,HANHui,WANG Jin-dong,XING Jun-jie
(Mechanical Science and Engineering Institute,Northeast Petroleum University,Daqing 163318,Heilongjiang China)
Reciprocating compressors are widely used in petroleum and chemical industries,but the overlarge clearance faults in the bearings of the compressors occur very often due to wear and tear.In this paper,considering the non-stationary and nonlinearity of the vibration signals of the reciprocating compressors,an improved Local mean decomposition(LMD)method is presented for the fault feature extraction of the reciprocating compressor bearings due to the large bearing clearance.To improve the accuracy of local mean and envelope estimation,a novel envelope-curve construction method is proposed by inserting an extremum symmetrical point between two extremum points and using the Monotonic Piecewise Cubic Hermite Interpolation(MPCHI)instead of Cubic Spline Interpolation(CSI).Algorithm and process of the improved LMD method are given.By comparing the decomposition results of the reciprocating compressor vibration signals with different LMD methods,the superiority of the improved LMD method is proved.Then,the overlarge bearing clearance fault is diagnosed accurately by the frequency spectrum envelope of the first PF component amplitude.
vibration and wave;reciprocating compressor;LMD;monotonic Hermite interpolation;bearing;fault diagnosis
TH212;TH213.3
ADOI编码:10.3969/j.issn.1006-1335.2016.04.028
1006-1355(2016)04-0135-05
2016-01-28
中国博士后科学基金资助项目(2015M581423);黑龙江省自然科学基金资助项目(E2015037);东北石油大学校内培育基金资助项目(XN2014105)
赵海洋(1979-),男,黑龙江省甘南县人,副教授,硕士生导师。现主要从事往复机械设备故障机理与诊断方法研究。
王金东,男,教授,博士生导师。E-mail:wjd327@126.com
