冲击荷载作用下轴向运动层合板非线性动力学响应

杨樟世，秦　营，李映辉

（西南交通大学 力学与工程学院，成都 610031）



冲击荷载作用下轴向运动层合板非线性动力学响应

杨樟世，秦营，李映辉

（西南交通大学 力学与工程学院，成都 610031）

研究轴向运动层合板在冲击荷载作用下的非线性动力学响应。基于单层材料本构关系及大变形理论，考虑几何非线性得到冲击荷载作用下的轴向运动层合板非线性动力学控制方程；通过Galerkin法对控制方程进行离散得到模态方程组，用Runge-Kutta法对模态方程组求解，得到冲击荷载作用下轴向运动层合板的动态响应。讨论了轴向速度、冲击波峰值和相位持续时间对轴向运动层合板动力学响应的影响。

声学；冲击荷载；轴向运动；层合板；几何非线性

层合结构常应用飞行器、空间站、汽车、潜艇等。这类结构有时处于运动状态，并受音爆、爆炸等冲击荷载作用。因此研究这类运动结构在冲击荷载下的非线性动力学行为具有学术理论和工程意义。

关于板在冲击荷载下的力学行为，Aaron等研究了矩形板在冲击荷载下的非线性动力学响应［1］。Zafer等研究了复合材料结构在各种冲击荷载下的非线性动力学响应［2-4］。Schiffer等基于实验和有限元法，讨论了水下冲击荷载下正交各向异性复合材料板的动力学响应［5］。Demet等对冲击荷载下黏弹性夹层板的动力学响应进行分析，并用有限元解和实验结果对其进行验证［6］。曾诚等考虑阻尼非线性特性，研究了非线性橡胶隔振器的冲击响应［7］。关于轴向运动板，刘金堂等研究了轴向运动板的非线性动力学行为［8］。李映辉等研究了轴线运动下黏弹性夹层板非线性动力稳定性［9］。李中华等讨论了轴向运动黏弹性夹层板的多模态耦合横向振动［10］。而目前未见轴向运动板在冲击荷载下的研究内容。

拟通过建立轴向运动层合板在冲击荷载下的非线性动力学方程，研究其非线性动力学响应，分析轴向运动速度、冲击波峰值和相位持续时间等对其动力学响应的影响。

1　控制方程

如图1、图2所示，层合板等效密度为ρ，第k层厚度为zk-zk-1，总厚度为H，长为a，宽为b，以速度νx沿x轴方向运动，受到冲击荷载P（t）的作用，其平衡方程为［10］

其中zk为第k层厚度方向坐标，Mx、My和Mxy为板内截面弯矩（扭矩），Nx、Ny分别为板内沿x方向、y方向的截面面力，Fxy为面内剪切力，w（x，y，t）为层合板的挠度，（·）x和（·）xx分别为对x的1阶和2阶偏导。考虑几何非线性，层合板几何方程为［9-10］

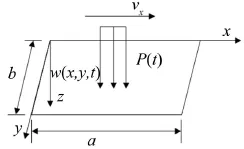
图1　层合板中面模型

图2　层合板截面模型

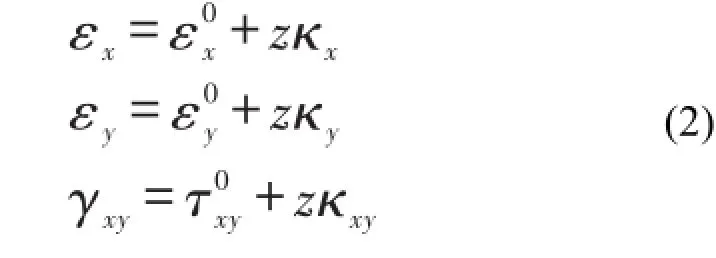
其中

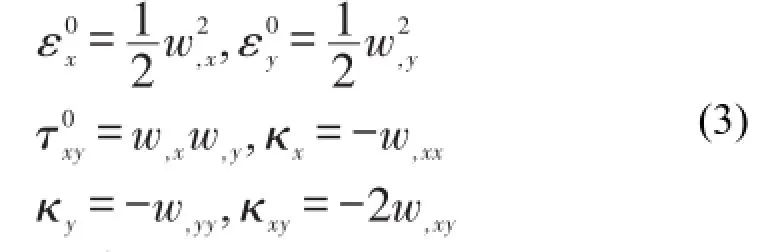
层合板本构方程为［11］

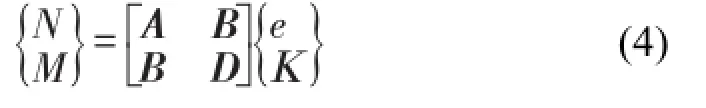
式（4）中

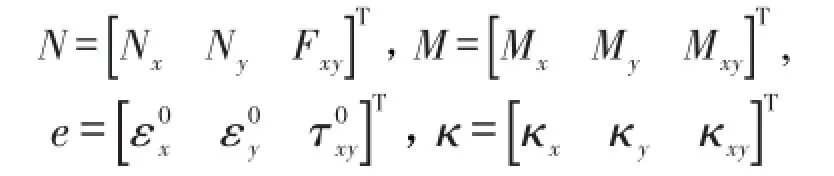
A、B、D分别为拉伸、耦合和弯曲刚度矩阵，其元素为［11］

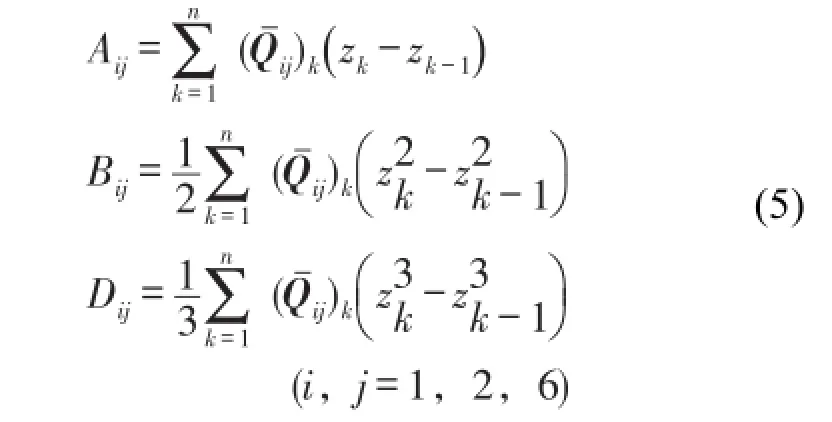
式（6）中

其中sn=sinq，cs=cosq，q为纤维方向角，Q11=E1/（1 -ν12ν21），Q22=E2/（1-ν12ν21），Q66=G12，Q12=ν12E1/（1-ν12ν21），其中E1和E2为主方向弹性模量，ν12和ν21为泊松比。

将式（4）代入式（1），得

式（9）中，冲击荷载P（t）一般形式为［1］

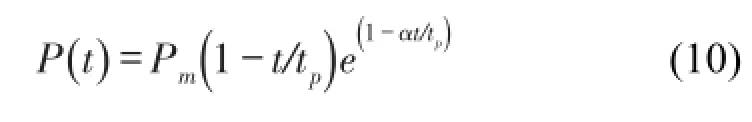
其中Pm为冲击荷载峰值，tp为相位持续时间，α=1.98为修正系数。

2　求解方法

假设式（9）的解为

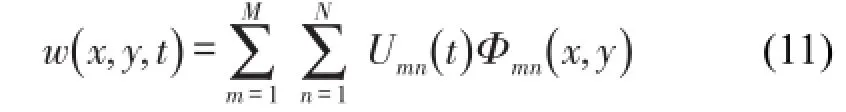
其中Fmn（x，y）是满足边界条件的试函数；M、N为截断阶数，代入方程（9），得到系统残差R（x，y，t），使用Galerkin法，得

对四边简支层合板，其边界条件为

3　数值结果与讨论

考虑两种材料组成的层合板，第一种材料为玻璃钢M300，各向同性，E1=9 140 MPa，ν12=0.326，单层厚度为0.01 m。第二种材料为玻璃钢W600，E1= 21 000 MPa，E2=20 500 MPa，ν12=0.137，G12=2 320 MPa，单层厚度为0.01 m。板长a=1 m，宽b=1 m，总厚度为0.04 m，等效密度ρ=1 680 kg/m3，铺层方式为（M300/W600）s，铺层角为（0°/90°）s，共4层。

3.1收敛性验证

取轴向运动速度νx=200 m/s，冲击荷载峰Pm= 3.447 MPa，相位持续时间tp=0.1 s，试函数［2-4］

取M=1，2，4，8，16，N=1，用Runge-Kutta法对式（12）进行求解，验证M变化时结果的收敛性，图3给出了板在（0.25 a，0.25 b）处的横向位移的峰值随M变化的规律。

图3　横向位移的峰值随M变化的规律（νx=200 m/s， tp=0.1s， Pm=3.447 MPa）

取M=1，N=1，2，4，8，16，验证N变化时结果的收敛性，图4给出了板在（0.25 a，0.25 b）处的横向位移的峰值随M变化的规律。

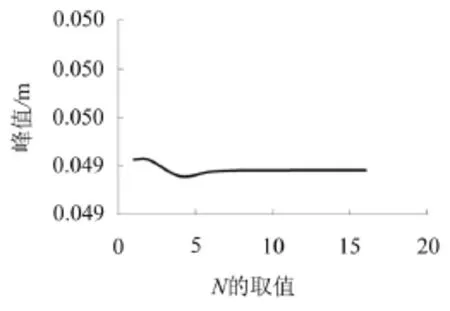
图4　横向位移的峰值随M变化的规律（νx=200 m/s， tp=0.1s， Pm=3.447 MPa）

图3中M=1时的峰值与M=16时的峰值相差16%，图4中N=1时的峰值与N=16时的峰值相差0.04%，可认为没有变化，故M可取16，N取1。有理由推出，不考虑速度项，由图4，可取M=N=1，这与文献［2-4］M和N的取值相同，故无需验证M=2时，N= 1，2，4，8，16和其他类似情况的峰值变化规律。

3.2有限元验证

将M=16、N=1的结果与有限元软件LS-DYNA的结果进行对比。图5给出了板在（0.25a，0.25b）处的横向位移随时间变化的规律，可见二者结果基本一致，说明本方法有效。

3.3轴向速度vx的影响

图6为轴向速度为νx、2νx、4νx时层合板动力学响应。可见，因陀螺效应，产生速度阻尼，所以速度越大，响应的幅值越小。

3.4冲击荷载峰值Pm的影响

图7为冲击荷载峰值为Pm、2Pm、Pm时层合板动力学响应。显而易见，增加峰值使幅值和频率变大。

图5　横向位移的峰值随M变化的规律（νx=200 m/s， tp=0.1s， Pm=3.447 MPa）

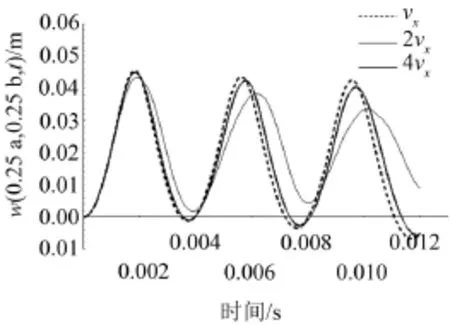
图6　轴向运动速度对板横向位移影响（tp=0.1 s， Pm=3.447 MPa， νx=50 m/s）

图7　冲击荷载峰值对板横向位移的影响（νx=200 m/s， tp=0.1 s， Pm=3.447 MPa）

3.5相位持续时间tp的影响

图8为相位持续时间分别为tp、2tp、4tp时层合板的响应。可见，相位持续时间tp越长，冲击荷载作用的时间越长，从而使幅值越大。

4　结语

基于单层材料本构关系及大变形理论，得到轴向运动层合板非线性动力学方程。用Galerkin法得到层合板动力学响应，结论如下：

因陀螺效应，产生速度阻尼，幅值随着速度增大而增大；冲击荷载峰值越大，响应频率越大，幅值越大；相位持续时间tp越长，冲击荷载作用的时间越长，幅值越大。

图8　相位持续时间对板横向位移的影响（νx=200 m/s， Pm=3.447 MPa， tp=0.005 s）

［1］AARON D G，FREDERICK H G.Dynamic analysis of an explosively loaded hinged rectangular plate［J］.Computer and Structures，1987，26:339-344.

［2］ZAFER K.Nonlinear damped vibrations of a laminated composite plate subjected to blast load［J］.American Institute of Aeronautics and Aastronautics Journal，2006，44:2002-2008.

［3］ZAFER K.Nonlinear dynamic behavior of simply supported laminated composite plates subjected to blast load［J］. Journal of Sound and Vibration，2008，317:883-897.

［4］ ZAFER K.Dynamic response of composite sandwich plates subjected to time-dependent press［J］.International Journal of Non-Linear Mechanics，2011，46:807-817.

［5］SCHIFFER A，TAGARIELLI V L.The dynamic response of composite plates to underwater blast theoretical and numerical modelling［J］.International Journal of Impact Engineering，2014，70:1-13.

［6］DEMET B，ZAHIT M.Nonlinear dynamic behavior of viscoelastic sandwich composite plates under non-uniform blast load:Theory and experiment［J］.International Journal of Impact Engineering，2014，72:85-104.

［7］曾诚，华宏星.非线性橡胶隔振器的冲击响应特性研究［J］.噪声与振动控制，2012，32（4）：20-24.

［8］刘金堂，杨晓东，张宇飞.轴向运动大挠度板的非线性动力学行为［J］.工程力学，2011，28（10）：58-64.

［9］李映辉，吕海炜，李中华.轴向运动黏弹性夹层板非线性动力稳定性分析［J］.重庆理工大学学报，2012，26（12）：16-20.

［10］李中华，李映辉.轴向运动黏弹性夹层板的多模态耦合横向振动［J］.复合材料学报，2012，29（3）：219-225.

［11］沈关林.复合材料力学［M］.北京：清华大学出版社，2006：50-99.

Nonlinear Dynamic Response of Laminated Plates with Axial Motion Subjected to Impact Load

YANG Zhang-shi，QINYing，LI Ying-hui

（School of Mechanics and Engineering，Southwest Jiaotong University，Chengdu 610031，China）

The nonlinear dynamic response of laminated plates with axial motion subjected to impact load is studied.Firstly，based on the constitutive relation of the material of each layer and large deformation theory，the nonlinear dynamical equation of the plates is obtained.Then，the modal equations are gained through Galerkin method and solved by Runge-Kutta method.Finally，the effects of axial motion velocity，the peak reflection pressure，the positive pressure phase duration of the impulse on the nonlinear dynamic response are investigated.

acoustics；impact load；axial motion；laminated plate；geometric nonlinearity

O422.6

ADOI编码：10.3969/j.issn.1006-1335.2016.04.004

1006-1355（2016）04-0021-03+37

2016-01-04

国家自然科学基金资助项目（11372257）

杨樟世（1990-），男，浙江省湖州市人，硕士研究生，研究方向为动力学与控制。E-mail:yinghui.li@swjtu.edu.cn