压电陶瓷在锥形圆筒振动主动控制中的应用

孙龙飞，李维嘉，吴耀中

（华中科技大学 船舶与海洋工程学院，武汉 430074）



压电陶瓷在锥形圆筒振动主动控制中的应用

孙龙飞，李维嘉，吴耀中

（华中科技大学 船舶与海洋工程学院，武汉 430074）

锥形圆筒结构被广泛应用在船舶、航天器等工程系统中，减小其振动具有重要意义。以单端固定的锥形圆筒为研究对象，将压电陶瓷粘贴在圆筒表面分别作为传感器及作动器组成减振装置。通过有限元方法得到结构固有频率及振型信息，并采用模态实验分析对仿真结果进行验证，仿真及实验结果相一致。根据结构的振动特性，设计多模态模糊滑模控制器对锥形圆筒各阶模态振动分别进行主动控制研究，得到时域及频域下实验结果，对比实验结果表明减振方法的可行性。

振动与波；锥形圆筒；压电陶瓷；模态分析；模糊滑模控制；振动控制

锥形圆筒结构被广泛应用在船舶、航天器等工程系统中，如船舶喷水推进导流管、航天器外壳等结构。它的振动具有许多危害，如可能影响船舶内部仪器的正常工作，可能增加噪声影响潜艇的隐身性能等［1］，因此了解它的振动特性并实现减振控制具有重要意义。压电陶瓷具有高频响应良好、小巧轻便等优良特性，在振动主动控制中具有广泛的应用前景。在压电智能结构主动减振控制算法中主要有速度反馈控制、位置反馈控制、最优二次控制、自适应控制等等。如Wu D采用速度反馈方法对柔性悬臂梁不同阶模态分别实现振动控制［2］。Li L设计了一种自适应模糊滑模控制器并成功将其运用在具有不确定性质量的压电悬臂梁结构减振控制之中［3］。Zorić N D设计自适应模糊最优控制器对悬臂梁进行减振控制并与LQR控制的结果进行比较［4］。缑新科采用LQR控制方法对压电层合板进行减振控制并取得良好效果［5］。Sethi V对框架结构进行系统参数辨识并通过极点配置方法设计控制器进行多模态振动控制［6］。Qiu Z对悬臂板上压电陶瓷的布置位置进行了研究并对比了PD及PPF控制方法的控制效果［7］。Sohn J W以圆柱壳为研究对象，分析了压电陶瓷作动器的最优配置位置并采用了LQR的方法对其进行减振控制［8］。LQR控制及极点配置法需预先知道减振对象精确的数学模型，模糊控制会导致系统的动态品质变差，常规滑模控制存在较严重的抖振问题。模糊滑模控制器综合模糊控制及滑模控制优点，减小抖振并具有较好的控制效果和鲁棒性，适合应用于难以获得精确数学模型的工程系统中。

文中以粘贴有压电陶瓷传感器及作动器的锥形圆筒作为研究对象，采用有限元方法得到结构的振型及固有频率特性，同时通过模态实验及系统参数辨识方法对有限元仿真结果进行验证，得到系统的状态空间方程参数。以此为依据设计和实现模糊滑模控制器，对不同的振动模态分别进行控制，实验结果验证控制方法的可行性。

1　锥形圆筒模态分析

1.1理论分析

机械系统振动的运动方程式为［9］

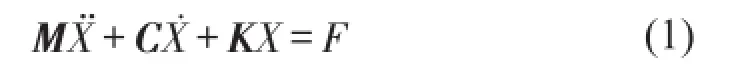
式中M、C、K分别为质量矩阵、阻尼矩阵及刚度矩阵，X为振动位移，F为外力。可以通过模态矩阵Φ将振动位移X转换为模态位移η，如下式所示。

将式（2）代入式（1），同时左乘模态矩阵的转置ΦT可得

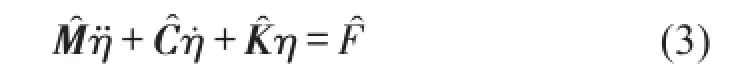
式中

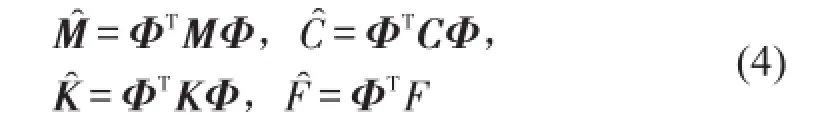
Mˆ、Cˆ、Kˆ分别为模态质量矩阵、模态阻尼矩阵及模态刚度矩阵，Fˆ为模态坐标下的控制力。从而得到模态坐标下振动方程的状态空间方程如式（5）所示。

式中

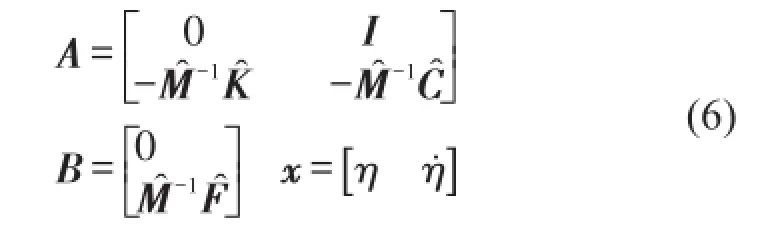
A、B、x、u分别为系统矩阵、输入矩阵、状态向量及控制输入矩阵。对于多模态振动的情况，考虑模态阶数为n，得到系统矩阵A，控制矩阵B及状态向量x如式（7）所示。

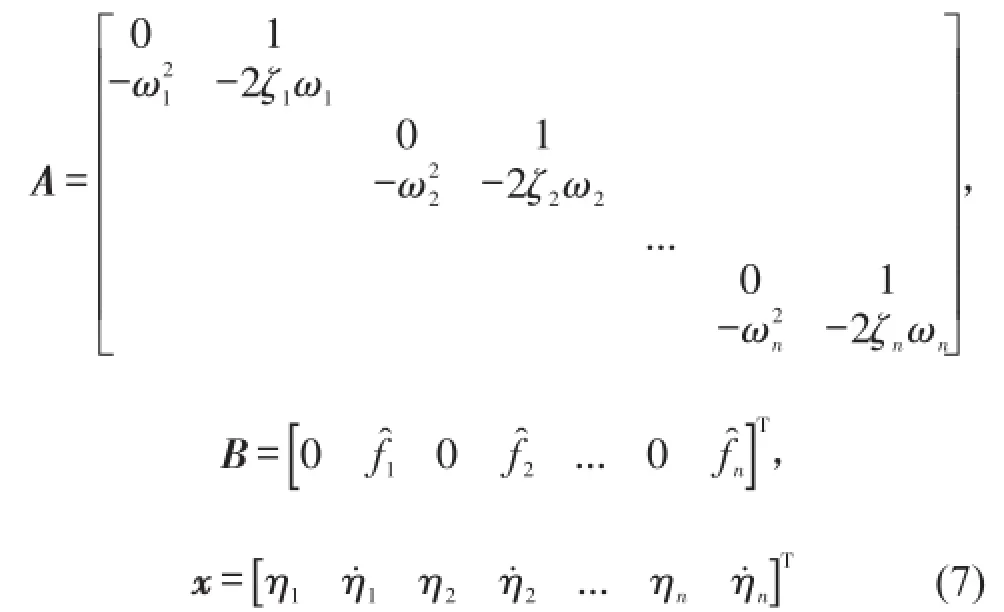
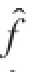
1.2有限元分析

模型结构为一个铝制锥形圆筒，锥形圆筒大端直径为300 mm，小端直径为200 mm，高度为500 mm，厚度为1 mm，模型小端直径固定。两片压电陶瓷器分别作为作动器及激振器对称地贴在锥形圆筒自由端的外表面，长度宽度及厚度分别为61 mm、35 mm、0.5 mm，另有一片陶瓷片作为传感器贴在作动器下面，长度宽度及厚度分别为16 mm、13 mm、0.5 mm。锥形圆筒模型结构如图1所示，铝合金及陶瓷片材料参数如表1所示。

图1　锥形圆筒结构及实验设备图

在不考虑压电陶瓷片对仿真结果影响的前提下，用Ansys对锥形圆筒进行有限元分析得到前4阶固有频率振型，如图2所示。

根据有限元分析结果，得到该结构前4阶固有频率分别为147.17 Hz、197.90 Hz、221.83 Hz、299.69Hz。同时从图2结果中可以发现，第1阶、2阶、4阶模态振型在自由端都有较大的应变，而第3阶模态振型则在固定端具有较大的应变，在自由端的应变几乎为零。因此在该结构中对于前4阶模态来说自由端具有更大的应变，所以文中压电陶瓷片选择贴在如图1所示应变较大的位置即薄壁圆锥筒的自由端。

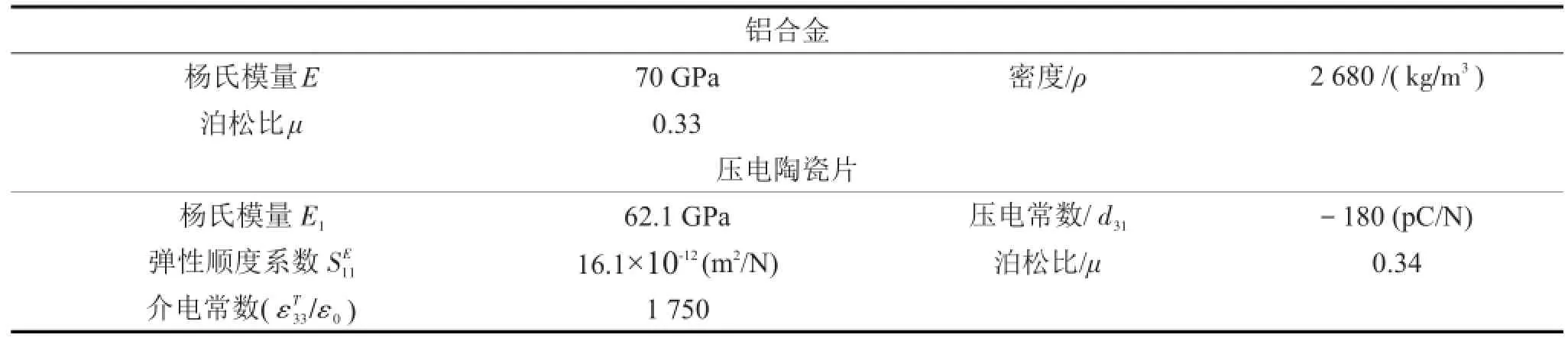
表1　材料参数表

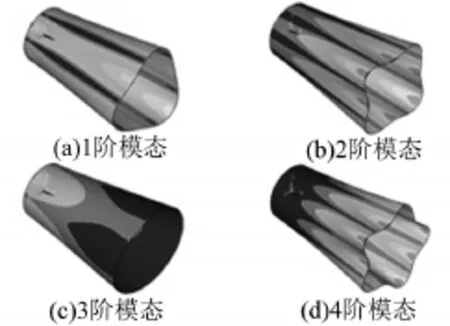
图2　锥形圆筒结构模型前4阶模态振型

1.3模态实验分析

为了验证有限元仿真结果的正确性并对实际模型结构有进一步的了解，进行模态实验［10］及参数辨识。实验设备如图1所示。由上位机产生50 Hz至500 Hz正弦扫频信号，通过工控机上的D/A转换模块及电压放大器将信号输出到压电陶瓷激振器。压电陶瓷传感器检测到振动信号，经由电荷放大器及工控机上的A/D转换模块将振动信号输入给计算机。编写程序对检测到的振动信号进行快速傅立叶变换，可以得到结构频率响应幅频特性曲线，如图3所示。

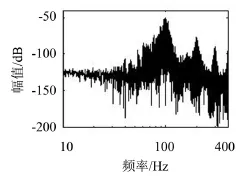
图3　模态实验幅频特性曲线

从幅频特性曲线上可以分析出结构固有频率信息。同时通过谱密度及相关函数对数据进行参数辨识［11-12］，可得到式（7）中各个参数信息。

模态实验所得到模型结构的1阶固有频率为101.5 Hz，2阶固有频率为197.6 Hz，4阶固有频率为301.9 Hz，3阶固有频率辨识结果不明显。根据前面Ansys分析结果知道，压电陶瓷传感器粘贴位置的第3阶模态应变几乎为零，因此也难以在该位置辨识出第3阶模态固有频率。综合Ansys仿真分析及实验结果，两者数据基本吻合，其中第1阶固有频率误差较大，可能是受到模型结构加工精度、陶瓷片粘贴位置等因素的影响。

2　独立模态模糊滑模控制算法

滑模变结构控制对系统的干扰和参数摄动具有完全自适应性，这是滑模变结构系统最突出的优点，具有广泛的实用性。

假设滑模面为

λ为一正常数。根据滑模变结构控制理论，λ的选择必须同时满足滑模存在性和可达性条件［13］，即使ss˙＜0。则滑模控制量ut取值为

式中sgn（）为符号函数。但是滑模运动会产生抖振问题［14］，为解决这一问题需要对控制器进行柔化处理。可以设计模糊控制器作为滑模控制增益以实现对滑模控制器的柔化。

设计模糊控制器［15］首先要选择输入及输出变量。选择模态位移η及模态速度η˙为模糊控制器输入量，控制电压为模糊控制器输出量。粘贴在锥形圆筒表面的压电陶瓷传感器，能够将检测到的振动信号转换为电压信号，电压信号经过模态滤波器处理之后，便可以得到系统的模态位移。取模态位移信号及模态速度信号的量化因子分别为ke和kec，则得到式（10）。

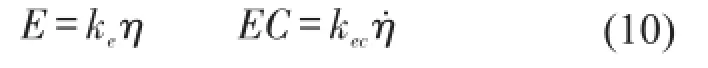
其中E、EC代表模糊集中的误差及误差的导数。

模糊控制器从传感器获取信号值，并通过模糊化转换为语言变量，选取NB、NS、ZE、PS、PB作为语言变量，输入输出隶属度函数设置如图4所示。根据Mamdani法，模糊规则可以写成式（11）所示形式。

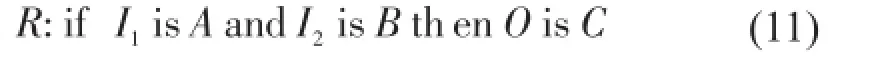
式中I1、I2代表输入变量，O代表输出变量，A、B、C为模糊变量的语言值。设置模糊规则表如表2所示。

由模糊推理得到的结果必须通过去模糊化转换为数值输出。通过这种过程模糊推理的结果能够转换为控制系统中实际应用的数值输出，去模糊的过程能够采用模糊规则表进行描述

其中u代表模糊控制器的输出，这里选择centroid去模糊化方法。同时可以通过输出信号比例因子ku对输出信号进行放缩，得到模糊滑模控制器的输出信号为

由于结构振动具有多阶模态特性，并且不同模态之间不存在耦合关系，这样就可以对不同模态分

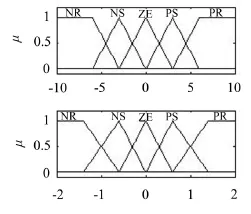
图4　输入（上）及输出（下）函数隶属函数曲线

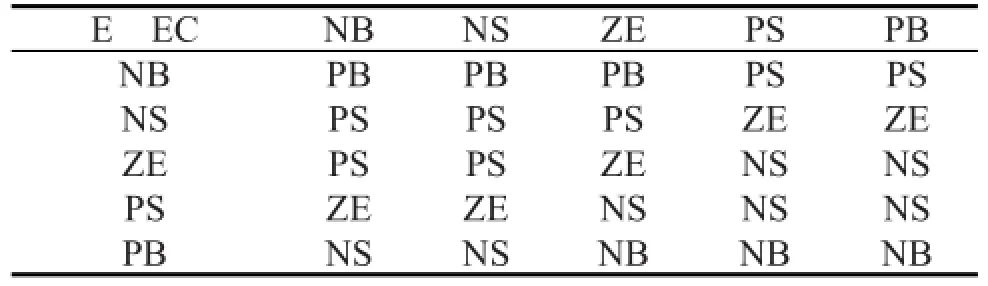
表2　模糊规则表

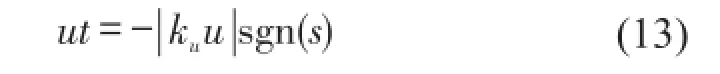
别进行控制，这为控制器的设计带来了便利。多阶模态模糊滑模控制器框图如图5所示：

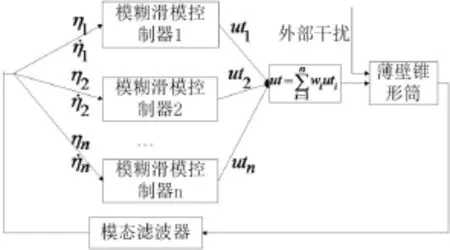
图5　独立模态模糊滑模控制示意图

其中uti为第i阶模态控制输出电压，wi为第i阶控制输出电压权值。将各阶模态的模糊滑模控制器线性叠加得到控制器输出电压。

3　实验结果

为评估主动减振控制算法的有效性，进行减振实验研究。结构振动的激振信号由工控机产生，并经过D/A转换模块及电压放大器传输给压电陶瓷激振器。设计的模糊滑模控制器的输入信号由压电陶瓷传感器检测并经由A/D转换模块传输给工控机。工控机中安装有Linux实时操作系统，并通过安装在上位机的Labview软件编写控制程序，上位机与工控机由以太网连接。在脉冲信号激励下，得到结构在加入控制和无控制情况下的频率响应，如图6所示。根据幅频特性，结构在1阶模态固有频率振动幅值减小约15 dB，2阶模态固有频率幅值振动减小约17 dB，4阶模态固有频率振动幅值减小约14 dB。

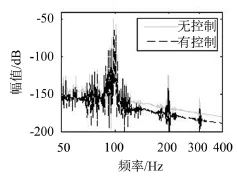
图6　有控制及无控制频率响应曲线

另外还进行了正弦激励实验，使用101.5 Hz的正弦激励信号，观察结构各阶模态振动。1阶模态的振动时域信号及作动器的总控制电压分别如图7及图8所示。

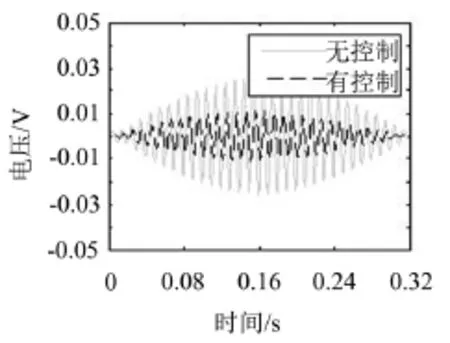
图7　1阶模态振动曲线

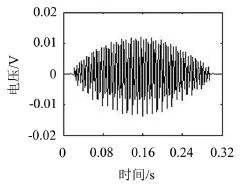
图8　控制电压曲线

可以看到振动信号的最大幅值由0.03 V减小为0.015 V左右，电压值减小约50%，减振效果较为明显。独立模态模糊滑模控制器的设计无需精确的数学模型，是将一个粗略复杂的多阶系统控制器设计转化为多个2阶子系统控制器的设计，这能够极大地简化控制器的设计难度，使控制器结合模糊控制及滑模控制的优点，具有良好的控制效果和鲁棒性，其在具有不确定性主动减振系统中的应用是行之有效的。

4　结语

将压电陶瓷粘贴在结构表面分别作为传感器及作动器，通过Ansys仿真分析及模态实验分析得到结构固有频率及振型等振动特性，为压电陶瓷片的粘贴位置及控制器的设计提供依据。

根据结构振动的非线性特性，设计模糊滑模控制器对振动进行控制。模糊滑模控制器结合了模糊控制及滑模控制两者的优点，具有一定的自适应性。同时由于各阶模态之间不具有耦合关系，针对各阶模态分别设计独立模态模糊滑模控制器进行减振控制，为减振控制带来了灵活性和便利性。从实验结果可以发现加入控制之后压电陶瓷检测到的信号减小，结构振动得到有效抑制。说明这是一个行之有效的控制方法，这为今后的研究提供了参考。

［1］李维嘉，曹青松.船舶振动主动控制的研究进展与评述［J］.中国造船，2007（2）：68-79.

［2］WU D，HUANG L，PAN B，et al.Experimental study and numerical simulation of active vibration control of a highly flexible beam using piezoelectric intelligent material［J］. Aerospace Science and Technology，2014，37:10-19.

［3］LI L，SONG G，OU J.Adaptive fuzzy sliding mode based active vibration control of a smart beam with mass uncertainty［J］.Structural Control and Health Monitoring，2009，18:40-52.

［4］ZORIĆ N D，SIMONOVIĆ A M，MITROVIĆ Z S，et al. Free vibration control of smart composite beams using particle swarm optimized self-tuning fuzzy logic controller［J］. Journal of Sound and Vibration，2014，333（21）:5244-5268.

［5］缑新科，崔明月.压电层合板的振动主动控制［J］.噪声与振动控制，2009，29（5）：50-53.

［6］SETHI V，S G.Multimode vibration control of a smart model frame structure［J］.Smart Materials and Structures，2006，15（2）:473-479.

［7］QIU Z，ZHANG X，WU H，et al.Optimal placement and active vibration control for piezoelectric smart flexible cantilever plate［J］.Journal of Sound and Vibration，2007，301（3-5）:521-543.

［8］SOHN J W，CHOI S，KIM H S.Vibration control of smart hull structure with optimally placed piezoelectric composite actuators［J］.International Journal of Mechanical Scences，2011，53（8）:647-659.

［9］任明章.机械振动的分析与控制及计算方法［M］.北京：机械工业出版社，2011.

［10］杜贵益.基于虚拟仪器的振动测试与模态分析系统研究［D］.长沙：中南大学，2010.

［11］李鹏波，胡德文.系统辨识基础［M］.北京：中国水利水电出版社，2006.

［12］曹青松.新型主动隔振系统的理论与实验研究［D］.武汉：华中科技大学，2007.

［13］陈志梅，王贞艳，张井岗.滑模变结构控制理论及应用［M］.北京：电子工业出版社，2012.

［14］GU H，SONG G，MALKI H.Chattering-free fuzzy adaptive robust sliding-mode vibration control of a smart flexible beam［J］.Smart Materials and Structures，2008，17（3）:4006-4032.

［15］黄卫华，方康玲.模糊控制系统及应用［M］.北京：电子工业出版社，2012.

Active Vibration Control of a Conical Shell Using Piezoelectric Ceramics

SUN Long-fei，LI Wei-jia，WU Yao-zhong

（School of NavalArchitecture&Ocean Engineering，Huazhong University of Science and Technology，Wuhan 430074，China）

Conical shell structures are commonly used in many engineering systems such as marines and spacecraft.Vibration suppression is an important problem in this application.In this study，a conical shell with piezoelectric actuators/sensors is considered in active vibration control.Finite element analysis is performed to get the natural frequencies and mode shapes of the structure.A modal test is carried out to verify the finite element analysis results.Both the results of natural frequencies are consistent.Then，according to the modal characteristics，a multi-modal fuzzy sliding mode controller is designed for the active vibration control test.The test results in time and frequency domains show that this controller is effective.

vibration and wave；conical shell；piezoelectric ceramics；modal analysis；fuzzy sliding mode control；vibration control

O328；TB535

ADOI编码：10.3969/j.issn.1006-1335.2016.04.040

1006-1355（2016）04-0188-05

2016-02-01

孙龙飞（1991-），男，辽宁省锦州市人，硕士研究生，研究方向为机电控制与仿真、振动控制。

李维嘉（1964-），男，教授、博士生导师，研究方向为水下作业系统、机电液智能控制系统、机器人。E-mail:liweijia@hust.edu.cn