新混沌系统的动力学分析及计算机仿真

李海洋,尹社会

(河南工业职业技术学院,河南 南阳　473000)



新混沌系统的动力学分析及计算机仿真

李海洋,尹社会

(河南工业职业技术学院,河南 南阳473000)

构造了一类新的含有包含绝对值的非线性项的三维二次自治混沌系统,根据稳定性理论分析了系统的定性行为,并借助Matlab软件进行了数值模拟,得到了系统的部分动力学特性。通过Lyapunov指数谱讨论了系统参数对系统混沌特性的影响,结果表明随着系统参数的变化,系统的动力学行为也发生了变化。进一步通过分岔图、Poincare截面图以及相图验证了上述结论。

混沌系统;动力学行为;分岔;Poincare映射

Lorenz混沌吸引子是最著名的混沌吸引子,被认为是第一个被发现的耗散系统混沌的实例。在发现了Lorenz混沌吸引子之后,又不断有新的混沌吸引子被发现,这些混沌系统的混沌特性被许多研究者所认识和研究。按照三维自治方程组的动力学行为由其线性部分决定的观点,除了著名的Lorenz系统族(包括Lorenz系统、Chen系统、Lü系统、Liu系统、Bao系统、T系统等)[1-6],还有很多超混沌系统也不断被发现和研究[7-11]。这些新系统的发现一般是利用混沌反控制思想来实现的,也有一些利用计算机模拟来随机构造。

在上述研究的基础上,提出了一个新的混沌系统,利用非线性动力学的方法,不仅通过常用的方法如理论推导、相图、时序波形图,还利用Lyapunov指数谱、Poincare截面图、分岔图和功率谱数值模拟研究了该系统的基本动力学特性,并分析了系统在不同参数时复杂的动力学现象,结果表明,系统在不同参数情况下具有丰富的动力学行为。

1　数学模型及主要结果

一个新构造的三维非线性自治混沌系统的方程为

(1)

其中:(x,y,z)T∈R3为状态变量,a、b、c、d为系统实参数。系统(1)除包含1个二次非线性项xz和1个三次非线性项yz2外,还有1个绝对值非线性项|xy|。这明显区别于Lorenz系统、Lü系统、Chen系统、Liu系统、Bao系统、T系统等,经过数值计算发现,当a=4,b=10,c=3,d=6时系统存在混沌吸引子。

1.1对称性和不变性

在变换P∶(x,y,z)→(-x,-y,-z)下所有的参数具有不变性,即系统(1)关于z轴是对称的。

1.2耗散性和吸引子的存在性

系统(1)的向量场散度为

(2)

根据刘维尔定理,当a-b-c<0时,系统(1)是耗散的,即系统(1)会以指数形式收敛,当t→∞时,包含系统(1)轨线的每个体积元都以指数速率a-b-c收缩到0,所以系统(1)的所有轨线最终都会被限制在一个体积为0的点集上,并且渐进动力学行为被固定在一个吸引子上。当a=4,b=10,c=3,d=6时,系统(1)的轨线的相图如图1所示。

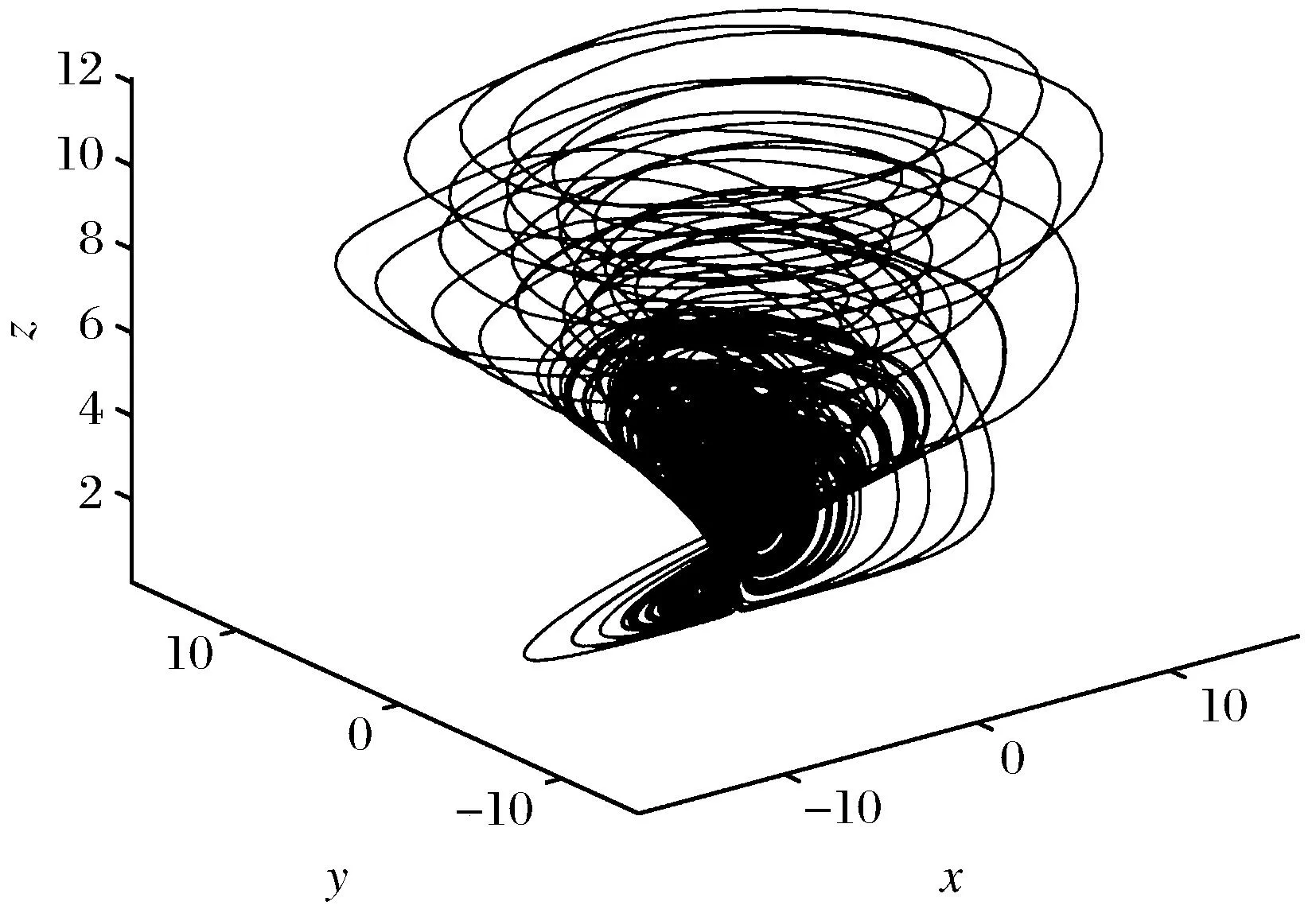
图1　系统(1)在参数a=4,b=10,c=3,d=6下的轨线相图Fig.1　Rajectory phase diagram of system (1) at constant a=4,b=10,c=3 and d=6

从时序波形图(见图2)也能看出,没有出现周期现象,如果初始条件发生微小的扰动,系统的时序波形图将会发生很大的改变,为了清楚表现这一特征,我们采用两个具有微小差别的初始值(只有0.000 01),让两个时间序列相减,得到初始敏感性时序波形图,如图3所示。

1.3平衡点及其稳定性

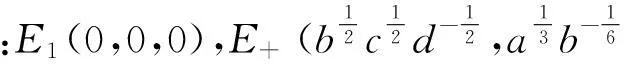
图2　系统(1)在a=4,b=10,c=3,d=6下的时序波形图Fig.2　Time-domain waveform of system (1) of each variable at the above parameters a=4,b=10,c=3 and d=6

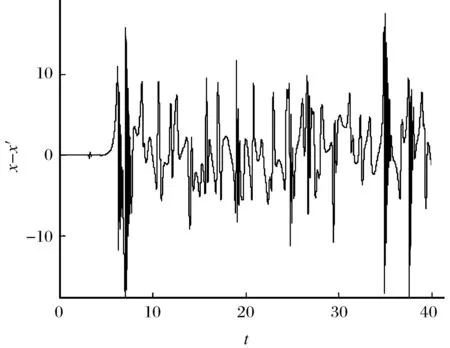
图3　系统(1)在a=4,b=10,c=3,d=6下的初值敏感性Fig.3　Initial value sensitivity of system (1) in the above parameters a=4,b=10,c=3 and d=6

当a=4,b=10,c=3,d=6时,这3个平衡点分别为E1(0,0,0)、E+(2.236,2.525,1.882)、E-(-2.236,-2.525,1.882)。系统(1)在平衡点E1(0,0,0)处线性化后的Jacobi矩阵为

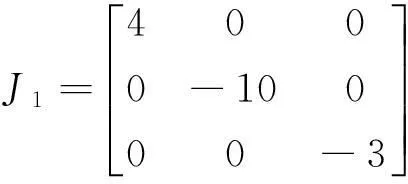
(3)

其对应的特征值为λ1=4,λ2=-10,λ3=-3,其中2个负根表示在这2个方向收缩,1个正根表示在这1个方向扩张。因此平衡点E0(0,0,0)为不稳定鞍点。

由于系统(1)关于z轴是对称的,E+和E-的稳定性相同,这里只讨论E+的情况。系统(1)在平衡点E+(2.236,2.525,1.882)处的线性化后的Jacobi矩阵为

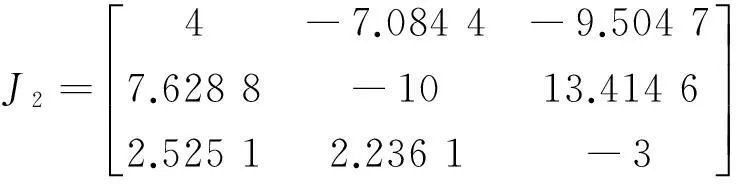
(4)

其对应的特征值为λ1=-12.257 7,λ2=1.628 8+7.912 8i,λ3=1.628 8-7.912 8i,其中1个负根表示在这1个方向收缩,1对共轭负根且实部为正表示在这2个方向螺旋扩张,负根的实部小于实根的绝对值,因此平衡点E+为不稳定指标2的鞍点。同理,平衡点E-也为不稳定指标2的鞍点。

1.4功率谱与Poincare截面

系统(1)在参数a=4,b=10,c=3,d=6下的功率谱表现出连续谱,并且有大量间断峰值出现,说明系统(1)处于混沌状态,如图4所示。Poincare截面是一种通过降低维数来研究问题的有效手段。系统(1)在参数a=4,b=10,c=3,d=6下的Poincare截面如图5所示。由图5可以看出,截面上具有明显的分形结构的密集点,说明系统(1)处于混沌状态。

2　参数对系统的动力学行为的影响

在计算Lyapunov指数谱时采用Wolf方法,其中数值模拟计算微分方程采用Runge-Kutta方法,通过设置合适的初始值和计算步长,可以得到系统(1)关于系统参数改变时的丰富动力学行为。

2.1参数a对系统的动力学行为的影响

固定参数b=10,c=3,d=6不变,改变参数a,a∈[0,7]。当参数a在区间[0,7]内变化时,系统随参数a的Lyapunov指数谱以及对应情况的分岔行为如图6所示。从图6上可以清楚的看出,随着参数a的从小到大a∈[0,4]的变化,系统(1)出现稳定平衡,经周期窗口过渡到混沌状态;从大到小a∈[4,7]由周期窗口反倍周期分岔到混沌状态。其中具体参数区间分布如下:稳定平衡态a∈[0,0.03);周期态a∈[0.03,0.5]∪[6.25,7];混沌态a∈[0.5,6.25]。

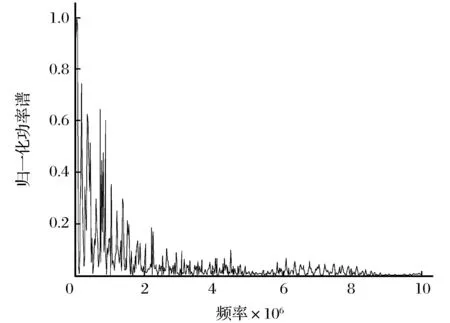
图4　系统(1)在参数a=4,b=10,c=3,d=6下的功率谱图Fig.4　Power spectrum chart of system (1) at the constant a=4,b=10,c=3, and d=6

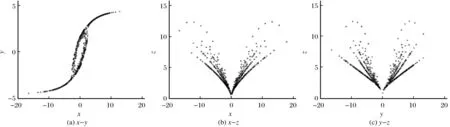
图5　系统(1)在参数a=4,b=10,c=3,d=6下的Poincare截面Fig.5　Poincare cross-section of system (1) at constant a=4,b=10,c=3 and d=6

2.2参数b对系统的动力学行为的影响

固定参数a=4,,c=3,d=6不变,改变参数b,b∈[5,50]。当参数b在区间[7,50]内变化时,系统随参数b的Lyapunov指数谱以及对应情况的分岔行为如图7所示。从图7可以很清楚的看出,随着参数b的改变,系统(1)出现混沌窗口和周期窗口交替出现的现象。

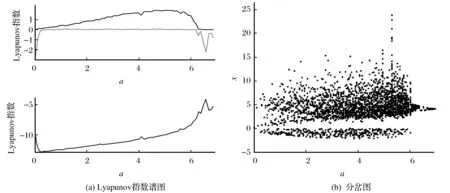
图6　系统(1)在参数b=10,c=3,d=6下的Lyapunov指数谱和分岔图Fig.6　Lyapunov exponent spectrum and bifurcation diagrams of system (1) in the parameter of b=10,c=3,d=6

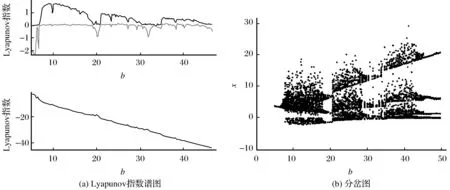
图7　系统(1)在参数a=4,c=3,d=6下的Lyapunov指数谱和分岔图Fig.7　Lyapunov exponent spectrum and bifurcation diagrams of system (1) in the parameter of a=4,c=3,d=6

2.3参数c对系统的动力学行为的影响

固定参数a=4,b=10,d=6不变,改变参数c,当c∈[0,6]时,系统随参数c的Lyapunov指数谱以及对应情况的分岔行为如图8所示。由图8可以看出参数c和参数a对系统的动力学行为的影响非常相似。

图8　系统(1)在参数a=4,b=10,d=6下的Lyapunov指数谱和分岔图Fig.8　Lyapunov exponent spectrum and bifurcation diagrams of system (1) in the parameter of a=4,b=10,d=6

2.4参数d对系统的动力学行为的影响

固定参数a=4,b=10,c=3不变,改变参数d,当d∈[0.1,6]时,系统随参数d的Lyapunov指数谱以及对应情况的分岔行为如图9所示。

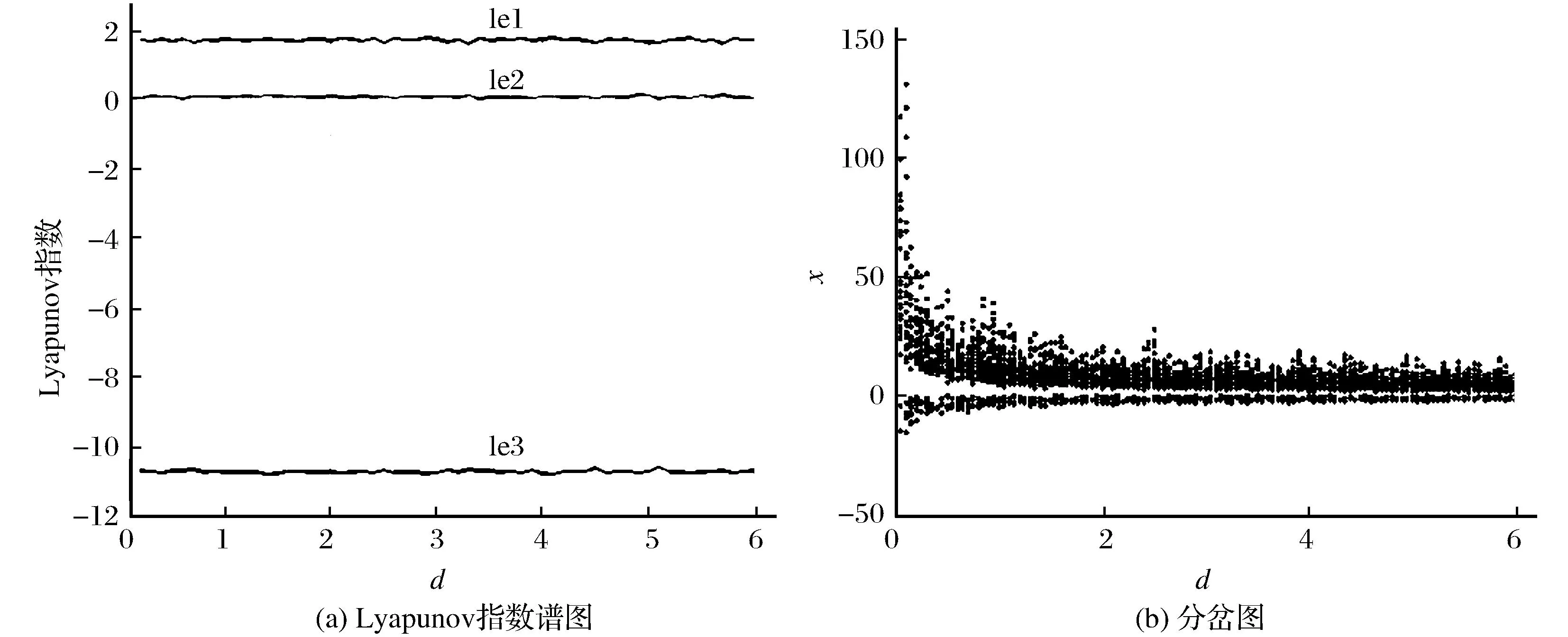
图9　系统(1)在参数a=4,b=10,c=3下的Lyapunov指数谱和分岔图Fig.9　Lyapunov exponent spectrum and bifurcation diagrams of system (1) in the parameter of a=4,b=10,c=3

从图9可以明显地看出,参数d对系统状态几乎没有影响,在所选取参数区间范围内,系统(1)所对应的Lyapunov指数恒定。其原因是,参数d在平衡点的Jacobi矩阵对应的特征方程中没有出现,即对特征值没有影响,所以相应的Lyapunov指数不变。

从上述讨论可以看出,系统参数对系统混沌行为的影响程度不同,其中参数d对系统状态的影响最小,这里从相图的角度给出几组具体参数对应的情况,如图10所示。

图10　系统(1)在不同参数下的相图Fig.10　Phase diagram of system (1) in the different parameters

3　结论

利用非线性动力学的方法并结合相应的计算机仿真,对新构造的三维自治混沌系统在参数变化时的部分动力学行为的变化进行研究。主要利用相图、Lyapunov指数谱图、分岔图、Poincare截面和功率谱等研究了系统的混沌运动,通过改变系统参数,发现该系统在不同参数下具有丰富的动力学行为,可以处于稳定态、周期运动以及混沌状态。由于该系统具有丰富的动力学行为,其中复杂的动力学特性仍待进一步研究和探索。

[1]E N Lorenz.Deterministic Non-periods Flows[J].J.Atoms.Sci.,1963,20(2):130-141.

[2]Chen Guanrong,UETA Tetsushi.Yet Another Chaotic Attractor[J].International Journal of Bifurcation and Chaos,1999,9(7):1 465-1 466.

[3]Lü Jinhu,Chen Guanrong.A New Chaotic Attractor Coined[J].International Journal of Bifurcation and Chaos,2002,12(3):659-661.

[4]Liu Chongxin,Liu Tao,Liu Ling,etal.A New Chaotic Attractor Chaos[J].Chaos,Solitons and Fractals,2004,(22):1 031-1 038.

[5]Bao Bocheng,Liu Zhong,Xu Jianping.New Chaotic System and Its Hyperchaos Generation[J].Journal of Systems Engineering and Electronics,2009,20(6):1 179-1 187.

[6]G H Tigan.Analysis of a Dynamical System Derived from the Lorenz System[J].Science Bull Poli-tehnica University of Timisoara,2005,50(64):61-72.

[7]尹社会,张勇,张付臣,等.基于Lorenz系统的强迫Lorenz混沌系统的动力学研究[J].东北师大学报:自然科学版,2014,46(1):42-47.

[8]尹社会,曹辉.一个4维超混沌类Lorenz系统动力学分析[J].广西物理,2014,35(4):14-19.

[9]高智中.一个新超混沌系统及其线性反馈同步[J].中山大学学报:自然科学版,2012,51(6):30-34.

[10]高智中,韩新风,章毛连.一个新的四维超混沌系统及其电路仿真[J].东北师大学报:自然科学版,2012,44(1):77-83.

[11]尹社会,张勇,皮小力.自治混沌系统的动力学行为及计算机仿真[J].广西物理,2015,36(1):32-37.

Dynamic Analysis of New Chaotic System and Its Computer Simulation

Li Haiyang,Yin Shehui

(Henan Polytechnic Institute,Nanyang 473000,China)

This paper constructs a new nonlinear term three-dimensional quadratic autonomous chaotic system that includes absolute value.And it analyzes the qualitative behavior of the system by stability theory analysis,and uses the Matlab software to make numerical simulation,obtaining the part of the dynamic characteristic of the system.It uses the Lyapunov spectrum to discuss the influence of system parameters on chaotic characteristics,and the results show that the dynamic behavior of the system also changes with the changes of system parameters.

Chaotic system;Dynamic behavior;Bifurcation;Poincare mapping

10.16468/j.cnki.issn1004-0366.2016.04.005.

2015-06-15;

2015-08-04.

南阳市科学技术发展规划项目(2013GG048).

李海洋(1982-),男,河南南阳人,讲师,研究方向为微分方程.E-mail:boblee82@163.com.

O241.84;O29

A

1004-0366(2016)04-0017-06

引用格式:Li Haiyang,Yin Shehui.Dynamic Analysis of New Chaotic System and Its Computer Simulation[J].Journal of Gansu Sciences,2016,28(4):17-22.[李海洋,尹社会.新混沌系统的动力学分析及计算机仿真[J].甘肃科学学报,2016,28(4):17-22.]