非接触感应耦合圆形空心线圈的耦合性能研究
2016-08-31改造者
改造者:吴 萍 罗 成
非接触感应耦合圆形空心线圈的耦合性能研究
改造者:吴 萍 罗 成
针对非接触感应耦合圆形空心线圈进行了计算研究。首先推导出圆形空心线圈的自感和互感公式,根据自感和互感计算出耦合系数。结合Matlab编程计算,分析了气隙、线圈半径、初、次级相同及不同半径下偏移量变化对耦合系数的影响。结果表明:耦合系数随气隙增大而减小;当初、次级线圈半径相同时,随着其半径的同时增大,耦合系数先增大后减小;当初、次线圈半径不同时,耦合系数随着初级线圈半径变化而减小,只当初、次级线圈半径相同时耦合系数最大;当初、次级线圈半径相同时,耦合系数随着初、次线圈偏移量的增大而减小;当初、次级线圈半径不同时,初、次级边缘正对位置耦合系数最大,随着偏移量的继续变化,耦合系数减小。
自从电磁感应原理于1931年被法拉第发现以来,电能传输在很长一段时间内都是靠导线接触式传输。十九世纪末,著名物理学家和电气工程师尼古拉斯拉开始研究无线传输并成为了研究该领域的鼻祖。但因为缺乏资金、技术落后等问题使无线能量传输在较长时间内发展缓慢。随着技术的发展以及无线传输电能越来越受到人们的重视,二十世纪后期,无线能量传输取得了迅速的发展。现如今很多领域已经应用了无线电能传输技术,如手机无线充电、城轨交通无线供电等。
非接触感应耦合电能传输技术是传统变压器在初、次级间形成一个气隙,通过初、次级间的感应耦合实现电能的无线传输,如图1所示。为了克服铁心重量和成本问题,初、次级采用空心线圈。但空心线圈耦合性能不强,为了提高能量传输效率,对于空心线圈的耦合性能的研究就显得非常重要。
本文针对圆形空心线圈耦合性能进行了计算分析,首先对圆形空心线圈的自感、互感公式进行了计算,主要探讨了初、次线圈半径、气隙、偏移量对耦合系数的影响。
圆形空心线圈耦合计算
圆形空心线圈自感计算
线圈自感为:

式中:Le为线圈外自感,Li为线圈内自感。
如图2所示,r1为线圈平均半径,r2为导线内半径,l1为导线中心线,l2为导线内侧边线,θ为r2的角度,Φ 为r2和r1之间的夹角。
线圈内自感公式为:

根据聂以曼公式,线圈外自感公式为:

推出外自感公式为:

圆形空心线圈互感计算

图1 分离变压器模型

图2 单匝圆形线圈自感计算

图3 单匝圆形线圈相对位置示意图
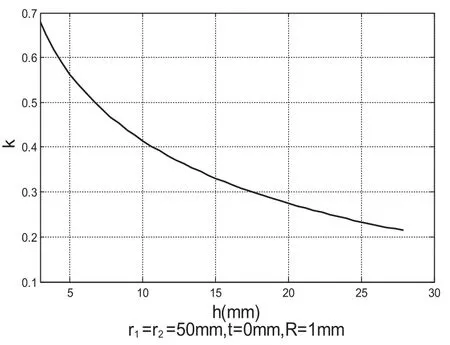
图4 耦合系数随气隙变化曲线

图5 耦合系数随线圈半径的变化曲线

图6 耦合系数随初级线圈半径变化曲线
如图3所示,t为初、次级线圈偏移量,h为初、次级线圈气隙,r1、r2为初、次级线圈半径,l1、l2为初、次级线圈1匝的长度。
根据聂以曼公式,线圈互感公式为:

推出互感公式为:
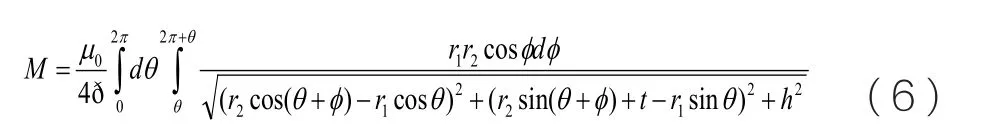
圆形空心线圈耦合系数的计算分析
耦合系数计算公式为:

由公式(1)~(7)可以得出圆形空心线圈的耦合系数。
耦合系数随初、次级气隙的变化
设圆形空心线圈初、次级线圈半径r1=r2=50mm,线圈导线半径R=1mm,初、次级偏移量t=0mm,则可以得到圆形线圈耦合系数随气隙变化的曲线如图4所示。
由图可以看出,耦合系数随初、次级气隙增大而迅速减小。
耦合系数随初、次级线圈半径的变化
设初、次级线圈半径r1=r2=r,线圈导线半径R=1mm,初、次级偏移量t=0mm,初、次级气隙h=3mm,如图5所示为耦合系数随线圈半径变化曲线。
由图可得,线圈半径在100mm以内时,耦合系数随着线圈半径的增大而增大较快;当半径在100mm与150mm之间时,耦合系数变化逐渐趋于平缓。当线圈半径大于150mm时,耦合系数随着线圈半径的增大而减小。当线圈半径r取100mm和150mm时,耦合系数分别为0.7279和0.7357。
耦合系数随初级线圈半径的变化
设初、次级线圈半径r2=50mm,线圈导线半径R=1mm,初、次级偏移量t=0mm,初、次级气隙h=3mm,如图6所示为耦合系数随初级线圈半径变化曲线。
由图可以得出,当初、次级线圈半径一样时,耦合系数取得最大值。当初、次级线圈半径相差越大,耦合系数就越小。
初、次级相同线圈半径下耦合系数随偏移量的变化
设线圈导线半径R=1mm,气隙h=3mm,如图7所示为初、次级相同线圈半径下耦合系数随初、次级偏移量的变化曲线。
从图中可以看出,变化趋势基本相同,三条曲线近似平行,随着偏移量的增大,耦合系数迅速减小。

图7 初、次级相同线圈半径下耦合系数随偏移量变化曲线

图8 初、次级不同线圈半径下耦合系数随偏移量变化曲线
初、次级不同线圈半径下耦合系数随偏移量的变化
当初、次级线圈长度不一样长时,设线圈导线R=1mm,气隙h=3mm,次级线圈半径r2=50mm,初、次级不同线圈半径下耦合系数随偏移量的变化曲线如图8所示。
由图可以看出,耦合系数随着初级线圈半径的增大而减小。在初、次级线圈半径比等于2条件下,当t/2r1=0.25时,耦合系数取得最大,即耦合系数在次级线圈边缘移动到和初级线圈边缘正对时取得最大。偏移量再增大时,耦合系数随之减小。
结语
本文对非接触感应耦合的核心部分圆形空心线圈进行了计算分析,推导出自感和互感计算公式,探讨了初、次级气隙、偏移量、线圈半径对耦合系数的影响。结果表明:
(1)耦合系数随初、次级气隙增大而减小。
(2)当初、次级线圈半径相同,取参数为线圈导线半径R=1mm,偏移量t=0mm,气隙h=3mm时,当其线圈半径小于150mm时,耦合系数随着线圈半径增大而增大;当线圈半径大于150mm时,耦合系数随着线圈半径的增大而减小。当初、次级线圈半径不同时,初、次级线圈半径相差越大,耦合系数就越小,当初、次级线圈半径一样时,耦合系数取得最大值。
(3)初、次级线圈半径相同时,耦合系数随着偏移量的增大而减小。初、次级线圈半径不同时,耦合系数在次级线圈边缘移动到和初级线圈边缘正对时取得最大值;偏移量再增大时,耦合系数随之减小。
DOI:10.3969/j.issn.1001-8972.2016.06.021
