装配式结构位移法分析中半刚性约束杆单元

韩明岚，陈建林，王　燕，王　慧

( 1.青岛理工大学理学院，山东青岛266033； 2.青岛理工大学土木工程学院， 山东青岛266033)



装配式结构位移法分析中半刚性约束杆单元

韩明岚1，陈建林1，王燕2，王慧2

( 1.青岛理工大学理学院，山东青岛266033； 2.青岛理工大学土木工程学院， 山东青岛266033)

为研究装配式半刚性钢框架结构的内力和变形，在各类理想约束杆转角位移方程和固端力计算公式基础上，根据半刚性节点刚度进行修正，得到各种半刚性约束等截面杆的转角位移方程、固端力计算公式、杆端转动刚度和传递系数等，并通过算例对半刚性钢框架结构进行计算，计算结果表明：节点刚度对结构内力和变形有着较大的影响，当半刚性节点刚度和柱线刚度比达到一定数值后，计算结果趋于平稳，说明当半刚性达到一定范围后可按照全刚性进行计算。

钢框架结构；半刚性；位移法；转角位移方程；固端弯矩；内力分析

0　引　言

位移法是一种基本且重要的结构力学计算方法，要顺利采用位移法对结构进行计算，一个重要的前提就是杆件的转角位移方程，无论是位移法基本方程还是典型方程，转角位移方程都是核心。在传统的结构中，理想的外部支座有固定端，固定铰支座，可动铰支座，定向支座等四种主要形式，内部节点简化为铰接或刚接，利用先拆后搭的思路，首先从结构中拆除杆件，即把结构中的构件全部拆成单跨杆件，杆件的约束取决于内部节点或外部支座。

随着绿色建筑技术的发展，呈现出越来越多的装配式建筑体系，各国专家也开展了装配式结构受力性能等方面的一些研究[1-3]，对一些集成的构件或模块进行现场安装，具有快速、方便、节省人力、施工受外界环境因素影响小等优点，装配式建筑技术是现代建筑工业技术发展的一种趋势和典型代表，对于装配式结构中梁柱节点，如图1所示，它不同于传统节点，也不同于新型延性耗能节点[4]，现场安装的特点很难保证节点是完全刚性的，所以装配式结构中多数节点均介于刚性和柔性之间，即为半刚性[5-6]，弹性范围内不同形式梁柱节点弯矩—转角关系见图2[7]，可见半刚接变形介于铰接和刚接之间，完全用刚接来取代是不合适的。因此探讨半刚性约束超静定等截面杆件的转角位移方程是很有必要的[8]，对解决简单装配式平面框架结构的内力分析及变形计算是很有帮助的。

1　理想约束单跨杆单元

图1　装配式节点Fig.1　Fabricated node

忽略轴力变形的影响，等截面杆单元变形见图3，杆长为l，刚度和线刚度分别为EI和i，杆两端节点转角分别为θA和θB，杆端弯矩分别用MAB和MBA表示，转角和弯矩以顺时针方向为正，两端相对竖向线位移为Δ，杆端剪力分别用FQAB和FQBA表示，位移和剪力均以顺时针转动趋势为正。

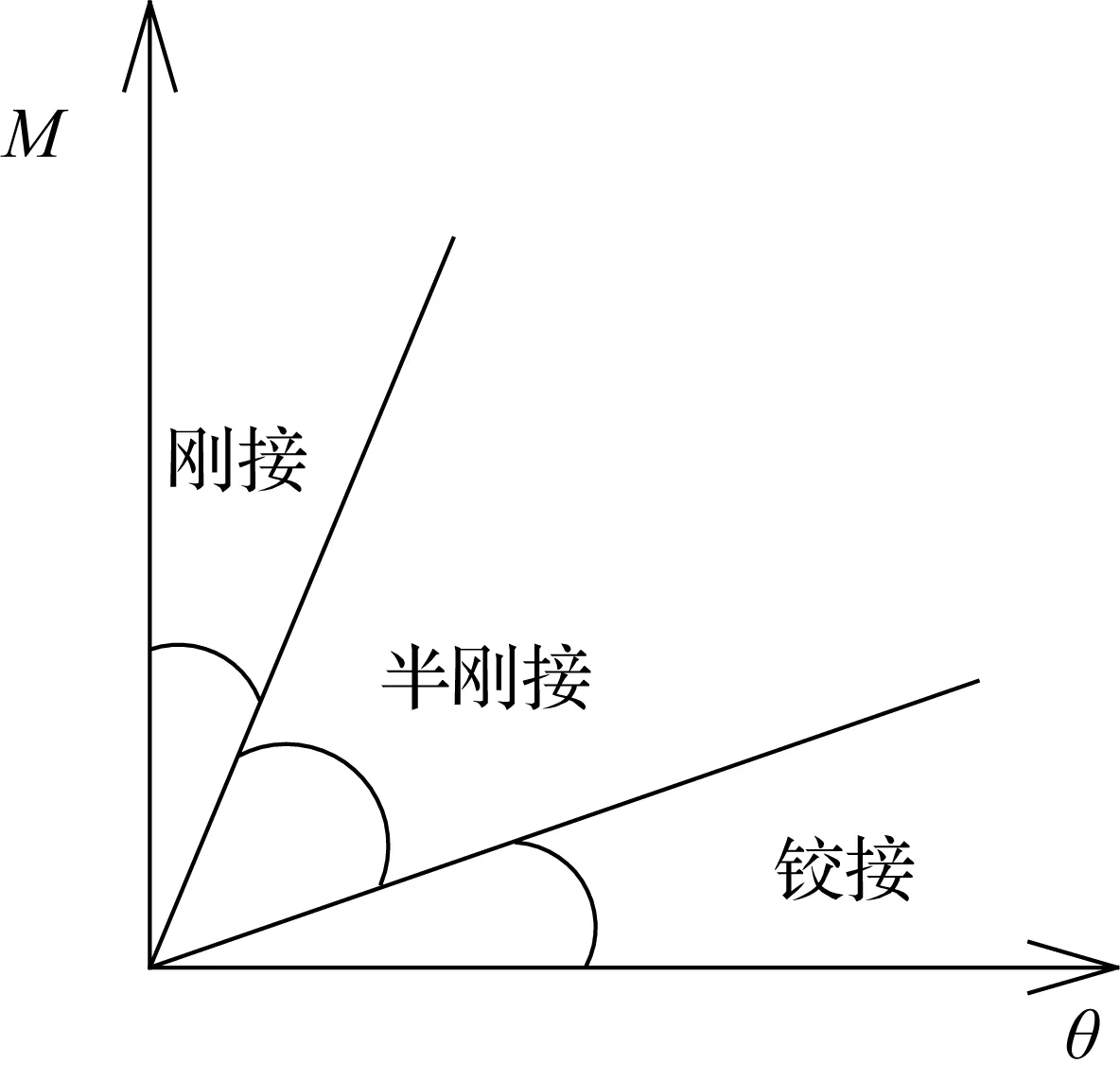
图2弯矩—转角关系

Fig.2Relationship of moment and rotation

图3杆单元

Fig.3Bar element

传统刚架中拆分的理想约束单跨超静定杆单元主要形式及对应的转角位移方程见表1，忽略杆件轴线变形，部分杆件形式可以进行合并。

表1　理想约束杆分类及其转角位移方程Tab.1　Classification of bar with ideal constraint and slope-deflection equation

2　装配式结构中半刚性约束杆单元

对于半刚性节点框架结构进行内力及变形计算，理想约束杆单元的转角位移方程就不适用了，需要对其进行调整或修正[9-10]，忽略杆件轴向变形，半刚性约束杆单元的主要形式见图4，用转动弹簧来模拟节点的半刚性。

(a) beam-1(b) beam-2(c) beam-3

(d) beam-4(e) beam-5(f) beam-6

若得到上述几种半刚性约束杆单元的转角位移方程和固端力，就可以利用位移法对半刚性节点框架结构进行内力和变形等方面的计算。

3　转角位移方程

由于杆端属于半刚性约束，当支座有主动位移时，杆端相对于支座就会产生被动角位移，因此杆端角位移就包含支座主动角位移和杆端相对于支座的被动角位移两部分，以下各杆单元中，杆长度均为l，杆两端主动角位移分别用θA和θB表示，主动竖向相对线位移用Δ表示，被动角位移用θA′和θB′表示，支座处转动刚度分别用KA和KB表示。不同类型约束杆单元对应着不同的转角位移方程。

3.1beam-1杆转角位移方程

若beam-1杆两端支座处均出现主动角位移时，变形见图5(a)，若beam-1杆两端有竖向相对线位移Δ时，变形见图5(b)。

(a) 两端主动角位移

(b) 两端相对竖向线位移

图5beam-1变形图

Fig.5Beam-1 deformation

图5(a)对应的杆端弯矩为：

(1)

其中：K=4(KA+3i)(KB+3i)-KAKB。

图5(b)对应的杆端弯矩为：

(2)

叠加式(1)和式(2)得到beam-1杆两端有主动角位移和主动竖向相对位移所对应的杆端弯矩：

(3)

3.2beam-2杆转角位移方程

当KB→∞时，beam-1转化为beam-2形式，调整式(3)得到beam-2杆单元的转角位移方程为：

(4)

3.3beam-3杆转角位移方程

beam-2杆当Δ不作为位移基本条件，且MAB=-MBA，对应beam-3杆形式，调整式(4)得到beam-3杆端对应的弯矩为：

(5)

当KA→∞时，MAB=-MBA=iθA-iθB，此时与beam 3形式一致。

3.4beam-4杆转角位移方程

beam-1杆当Δ不作为位移基本条件，且MAB=-MBA，对应beam-4杆形式，调整式(3)得到beam-4杆端对应的弯矩为：

(6)

当KB→∞时，beam-4杆形式转化为beam-3杆形式，杆端弯矩对应式(5)。

3.5beam-5杆转角位移方程

beam-1杆若KB→0，且θB不作为基本位移条件，此时与杆beam-5形式一致，调整式(1)得到beam-5杆端对应的弯矩为：

(7)

3.6beam-6杆转角位移方程

beam-6杆右侧拉压弹簧刚度定义为KB，由力法导出杆端弯矩：

(8)

通过beam-1～beam-6杆单元转角位移方程的推导，并进行彼此验证，说明公式推导是正确的，只要知道约束处的刚度，根据对应的杆单元形式就可以利用转角位移方程进行计算。

4　转动刚度及传递系数

根据各种半刚性杆的转角位移方程，可以得到杆端转动刚度和传递系数，见表2，杆端转动刚度和传递系数是力矩分配法计算的基础。

表2　杆端转动刚度及传递系数Tab.2　Rotational stiffness of bar end and carry-over factor

通过表2可以看出：半刚性约束杆转动刚度均比理想约束杆转动刚度降低，约束减弱，转动刚度自然降低。beam-1杆A端由于半刚性，其转动刚度介于0～4i，而B端为固定端，但受A端半刚性约束的影响，其转动刚度介于3i～4i，传递系数介于0～0.5；beam-2杆转动刚度介于3i～4i，传递系数介于0～0.5；beam-3杆和beam-4杆转动刚度均介于0～i；beam-5和beam-6杆转动刚度均小于3i。

5　固端弯矩

在位移法进行计算的过程中，除转角位移方程还需要知道固端力，应用力法对beam-1～beam-6杆在常见外部荷载作用下的固端弯矩进行计算(计算过程略)，分别对全杆作用均布荷载，荷载集度为q，以及跨中作用集中力P两种工况进行分析，固端弯矩计算结果见表3。通过表3可以看出：半刚性约束减弱，杆端的承载力较刚性约束杆端承载力相应降低。

表3　杆固端弯矩Tab.3　Bar fix-end moment

6　算例分析

利用本文推导的转角位移方程和固端弯矩对半刚性框架结构进行计算，结构见图6，假设图6(a)和图6(b)中B节点和C节点均为半刚性，刚度分别为KB和KC，且KB=KC，梁柱刚度均为EI，则两个框架均为对称结构，利用对称性取半结构进行计算，半结构见图6(c)和图6(d)，柱线刚度用i表示，则半结构中梁线刚度为2i。

(a) 均布荷载作用半刚性框架

(b) 侧向力作用半刚性框架

(c) 均布荷载作用半结构

(d) 侧向力作用半结构

图6半刚性钢框架结构

Fig.6Semi-rigid steel frame structures

图6(c)中，基本位移未知量为θB，AB杆对应beam-2形式，BE杆对应beam-3形式，利用对应的转角位移方程和固端弯矩进行计算杆端弯矩：

利用B节点弯矩平衡可以得到：

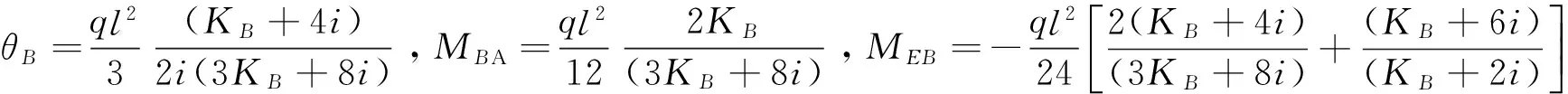
用MATLAB数值语言描述E处和B处截面弯矩数值与KB/i的关系，见图7。从图7中可以看出：节点刚度对跨中弯矩及梁端弯矩有着较明显的影响，随着节点刚度的增加梁端弯矩值增加，跨中弯矩值减小，当KB/i值小于10时影响较明显，当KB/i值大于20时，趋于平稳，逐渐逼近全刚接框架内力值。

图6(d)中BE杆对应beam-5形式，基本位移未知量为θB和侧移Δ，见图6(d)，则对应的杆端弯矩分别为：

计算后得到B端转角，侧向位移△和梁端弯矩MBA分别为：

刚架侧移量Δ和梁端弯矩与B节点刚度关系见图8和图9，从图8和图9中可以看出B节点刚度与框架侧移以及梁端弯矩成非线性关系，侧移量随刚度的增加而减小，梁端弯矩随刚度增加而增加，当KB/i值小于10时影响较明显，当KB/i值约大于20时，趋于平稳，逐渐逼近全刚接框架计算结果。

图7梁端、跨中弯矩值与B节点刚度关系

Fig.7Relationship of beam end moment, middle-span moment andBnode stiffness

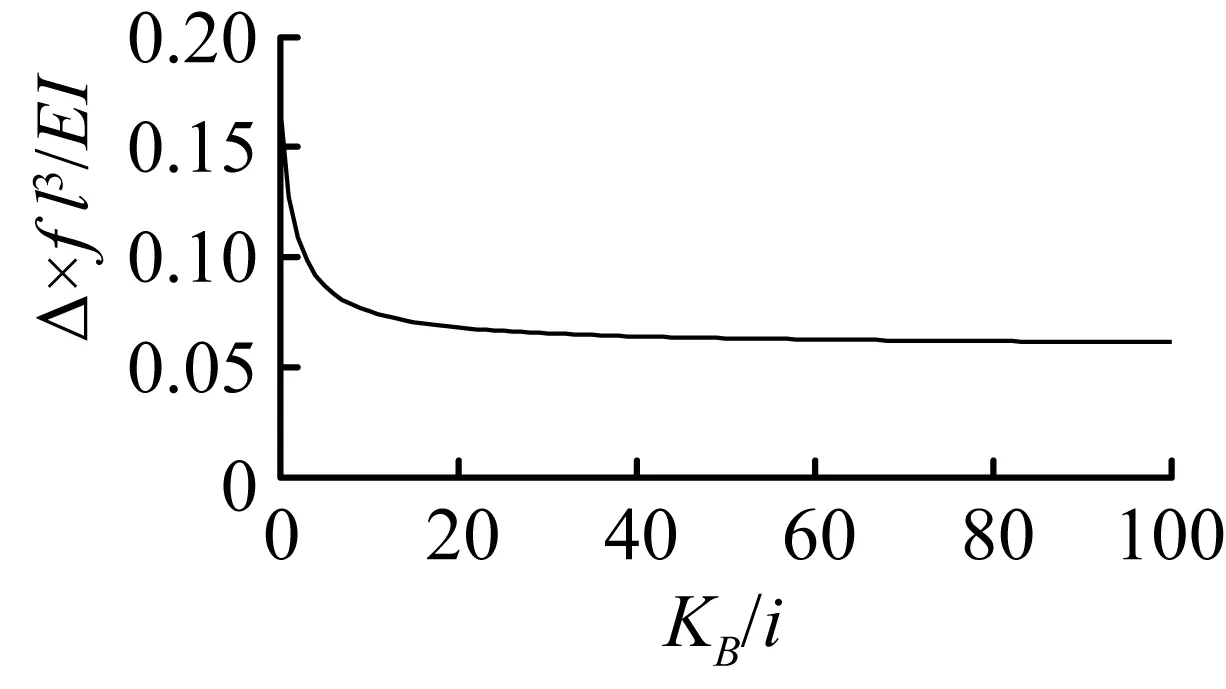
图8侧移Δ与B节点刚度之间的关系

Fig.8Relationship of lateral sway Δ and B node stiffness

图9梁端弯矩值与B节点刚度关系

Fig.9Relationship of beam end moment andBnode stiffness

7　结　语

针对装配式半刚性钢框架结构进行内力和变形分析，通过理论推导并进行计算得到结论：

①通过对半刚性约束杆单元进行分析，得到等截面直杆的转角位移方程、杆端转动刚度，传递系数以及固端弯矩等量，为半刚性约束钢框架结构进行内力及变形分析提供方便，只要获取节点的初始刚度，可以借助有限元或实验方法获取节点刚度，就可以对简单框架套用本文推导出来的公式进行计算，或者将本文推导公式程序化，这样对半刚性框架结构进行计算时只需要输入外部荷载，外部约束以及内部节点的刚度就可以进行内力和变形的分析。

②分析表明半刚性约束较理想刚接约束，其刚度降低，杆端承载力降低，杆端转动刚度及传递系数也相应下降，理想约束和半刚性约束条件不同，因此在实际工程中，尤其是装配式结构中，考虑节点的半刚性是很有必要的，若按照理想约束进行计算，将高估节点的承载能力。

③计算表明当节点刚度与柱的线刚度比超过一定值后，计算结果趋于平稳，说明当节点并非全刚性，但刚度相对比较大时，其计算结果与全刚性差别不大。

[1]刘学春, 林娜, 张爱林,等.梁柱螺栓连接节点刚度对装配式斜支撑钢框架结构受力性能影响研究[J]. 建筑结构学报, 2016,37(2):65-72.

[2]ANNAN C D, YOUSSEF M A, NAGGAR M H. Seismic vulnerability assessment of modular steel buildings[J]. Journal of Earthquake Engineering, 2009, 13(8)：1065-1088.

[3]HONG S G, CHO B H. Behavior of framed modular building system with double skin steel panels[J]. Journal of Constructional Steel Research, 2011, 67(6): 936-946.

[4]李泽深,谭达威, 张克实,等.不同构造T形钢连接节点受力性能分析[J]. 广西大学学报(自然科学版), 2016,41(1):74-82.

[5]王燕.钢结构半刚性连接设计理论及其工程应用[M]. 北京: 中国建筑工业出版社, 2011.

[6]李黎明, 陈以一, 李宁,等.外套管式梁柱节点弯矩—转角关系控制参数研究[J]. 工程力学, 2010, 27(7): 126-130.

[7]HASAN R, KISHI N, CHEN W F. A new nonlinear connection classification[J]. Journal of Constructional Steel Research, 1998, 47:119-140.

[8]王燕, 厉建芬.半刚性框架的内力分析[J]. 力学与实践, 2003, 25(2):35-38.

[9]王书报, 张红光,单俊虹.一类非理想杆端约束下的转角位移方程[J]. 工程力学, 2004, 21(3): 201-203.

[10]何剑平, 陈卫忠.弹性支座分析及其应用[J]. 力学与实践, 2011, 33(4): 17-22.

(责任编辑唐汉民梁碧芬)

Semi-rigid constraint bar in displacement method analysis of fabricated structure

HAN Ming-lan1, CHEN Jian-lin1，WANG Yan2, WANG Hui2

(1.School of Science, Qingdao University of Technology, Qingdao 266033, China;2.Department of Civil Engineering, Qingdao University of Technology, Qingdao 266033, China)

To analyze the internal force and displacement of fabricated semi-rigid steel frame structures, based on the slope-deflection equation and fixed-end moment formulation of bars with ideal constraints, the slope-deflection equation, fixed-end moment formulation, rotational stiffness and transfer coefficient of semi-rigidly constrained bar are deduced according to node stiffness, and a semi-rigid steel frame structure is analyzed. The results show that node stiffness has great effect on the internal force and displacement of the structure. However, calculated results are steady when the ratio of semi-rigid stiffness to column linear stiffness is up to certain value, which indicates that it can be calculated under the condition of full rigid when semi-rigid reaches a certain range.

steel frame structure; semi-rigid；displacement method；slope-deflection equation；fixed-end moment；internal force analysis

2016-02-25；

2016-04-01

山东省自然科学基金资助项目(ZR2012EEL26)；青岛市建设科技计划项目(JK2014-08)；青岛理工大学名校工程建设教学改革子项目(MX4-009)

韩明岚(1974—)，女，山东日照人，青岛理工大学副教授，博士;E-mail:zihanc@163.com。

10.13624/j.cnki.issn.1001-7445.2016.1037

TU391;TU311

A

1001-7445(2016)04-1037-08

引文格式：韩明岚，陈建林，王燕,等.装配式结构位移法分析中半刚性约束杆单元[J].广西大学学报(自然科学版)，2016，41(4)：1037-1044.