建筑物对屋顶风场的影响
2016-08-30李正农
李正农,耿 燕
(湖南大学建筑安全与节能教育部重点实验室, 湖南长沙410082)
建筑物对屋顶风场的影响
李正农,耿燕
(湖南大学建筑安全与节能教育部重点实验室, 湖南长沙410082)
目前,高层建筑台风风场实测的主要方法是在其顶部上架设风速仪获得相关数据,但高层建筑物顶部的风场将受到其本身的影响,而且其影响程度会随着风速仪架设的位置和来流方向的不同而发生变化。通过数值模拟和风洞试验模拟实测时的边界层风场,分析高层建筑对周边风场的影响,对比风向角变化时建筑物顶面风场在两种方式的吻合情况。研究得出建筑物顶面的风速随高度增加影响逐渐减小,确定了高层建筑风场实测时风速仪架设的高度和最佳位置。通过谱合成法生成入口条件,进行大涡模拟并研究了高层建筑对于本身风场的影响及与未受干扰的来流风场之间差别,为相似建筑的现场实测提供参考。
高层建筑;风场;风洞试验;数值模拟
0 引 言
在我国东南沿海区域,强台风登陆常常造成人员伤亡和很大的财产经济损失。但是,关于沿海区域不同的地貌类型、测点高度上的大气边界层风场特征的实测数据资料还不太完善,特别是强台风特征的实测还有些缺少。近年来,随着结构风工程研究的深化,大气边界层的风场特性的实测研究也受到更多的重视[1-3]。目前,对于台风风场现场实测比较理想的方法是在建筑物附近设立独立桅杆,再通过桅杆上安装的相应风速、风向测量仪器获得建筑物附近的来流风场信息[2]。然而,要在建筑前面建立与建筑物有相当高度的独立桅杆显然难以实现。目前高层建筑风场实测,主要通过在高层建筑物顶部上架设的风速仪采集,虽然其实测的风场数据基本上没有受到周围环境的影响,但不可否认的是其测得的风场数据将受到其建筑物本身的干扰,而风速仪在建筑顶面架设的位置和高度及来流方向的不同会对风场数据的准确采集产生一定程度的影响。
实测表明,高层建筑附近的边界层风场为非定常的,建筑本身的阻流作用增加了来流的脉动效应,大尺度脉动特征与钝体结构的建筑外形有关,比如流体在建筑物边缘的分离、附着、停滞以及漩涡等。常用的数值模拟方法[4-6]是模拟定常的大气边界层,分析建筑的平均风速风压特性,无法确定脉动风速和脉动风压特性;风洞实验和现场测试的数据[5-9]说明,建筑物周围的脉动风压的极值可能是平均风压值的几倍。因此,采用大涡模拟(LES)研究绕流风场的脉动信息对于建筑物抗风有重要意义。在建筑物流场非定常模拟中,常用的脉动入口的合成方法分别为预前模拟法[10]、旋涡法和谱合成法[11-13]。
本文通过使用挡板、粗糙元和格栅的设置,在HD-3风洞实验室中模拟大气边界层风场的平均风速度剖面、湍流强度剖面和脉动风特征,并通过计算流体力学(CFD)数值模拟方法进行稳态流场和非稳态流场下的大气边界层风场特性分析。研究了建筑物顶面的风速随测点高度变化规律,确定了高层建筑风场实测时风速仪架设的最小高度和最佳位置,并分析了高层建筑屋顶架设的风速仪采集的风场信息与未受干扰的来流之间差异,为相似建筑的现场实测提供参考。本课题组开展了某高层建筑的台风风场和风致响应的研究,故本次将以某高层建筑来进行风洞试验和数值模拟[1]的研究工作。

图1 平均风速剖面和湍流强度Fig.1 Vertical value of wind speed and turbulence intensity
1 风洞试验
1.1试验设备及试验模型
风洞实验是在湖南大学的HD-3大气边界层风洞实验室操作,风洞试验段的长度为12 m、宽度为3.5 m,高度为2.5 m,试验段的平均风速0~20 m/s 连续可调。考虑到建筑的尺寸和风洞试验段尺寸,试验以某高层建筑为中心进行,其尺寸为30.4 m×61.28 m×146.7 m,模型几何缩尺比为1∶200,截面尺寸为310 mm×154 mm×750 mm。分析高层建筑所处的位置,属于A类地貌,取α=0.12。选用劈尖、粗糙元的设模拟高层建筑所处的大气边界层,测得平均风速剖面和湍流强度如图1。
选用指数律形式的表达式描述平均风速剖面为:

(1)

依据我国现行建筑荷载规范,湍流强度随高度的分布规律采用式(2)和式(3)计算:

(2)

(3)
式中,Iu(z)为z高度处的湍流度;I10为距离地面10 m高度的名义湍流度,此时A类地面粗糙度指数选用 0.12;z为离地高度;α为地面粗糙度指数,同式(1)。
1.2试验工况定义
现场实测时风速仪架设在建筑顶面东面位置A处,如图2所示。实验时用眼镜蛇测量模型位置A处实际距建筑顶面4、8、14和20 m高度处的风速值。采用顺时针方向增量定义风向角,每15°采集一次相应数值,总共进行了风向角为0°~180°的风洞试验(图3)。
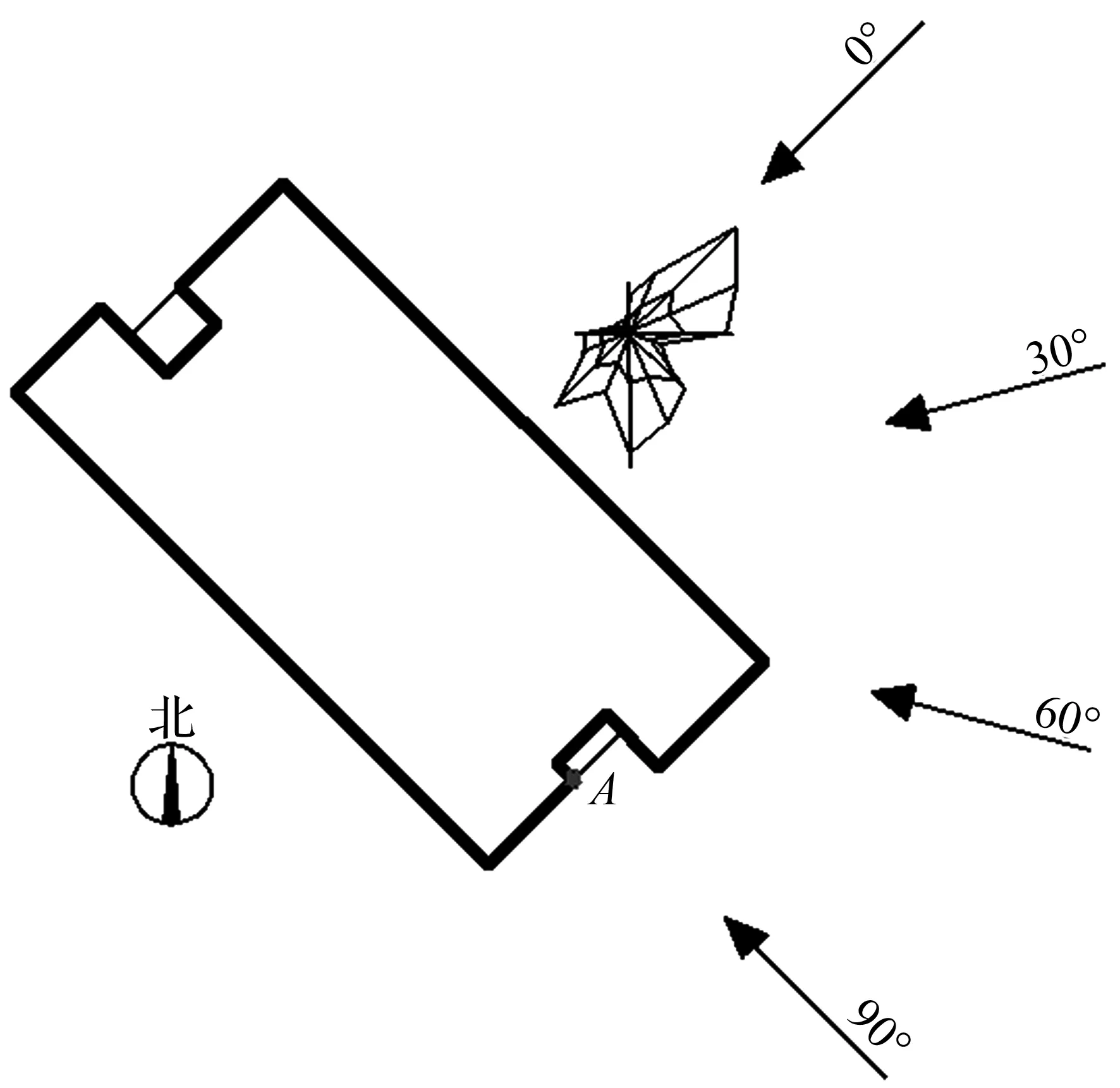
图2风洞试验的风向角
Fig.2Wind direction angles in the wind tunnel test

图3风洞试验模型
Fig.3Wind tunnel test model
2 数值模型
2.1控制方程
模拟建筑物周围流场时,可将选用不可压缩的粘性牛顿流体,钝体绕流的控制方程为粘性不可压连续方程和Navier-Stokes方程,RANS方法的连续性方程和动量方程为:
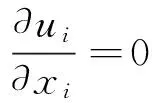
(4)
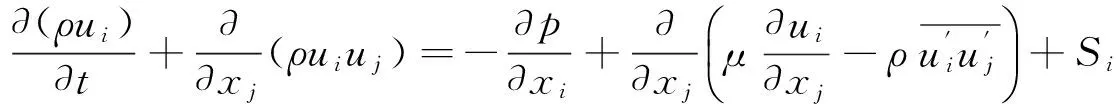
(5)
式中:ui为流体微元体速度场在i方向的分量值;ρ为流体密度;p为风压;Si为ui的源项。
而对于非定常风场,需要采用大涡模拟(LES)。大涡模拟是通过直接模拟大尺度脉动的湍流情况,对于受流动边界的影响较小的小尺度脉动湍流情况,采用亚格子模型描述其动量和能量传递对大尺度湍流脉动的作用。相对于RANS方法,LES模拟中没有对时间取平均,因此能够真实描述随时间变化的瞬时流场的详细特征。
2.2计算模型及网格划分
某高层建筑尺寸为30.4 m×61.28 m×146.7 m,采用足尺建模,计算流域为1 070 m(长) ×600 m(宽) ×450 m(高),模型放于入口50 m处,数值模拟时流场满足阻塞率小于3%。
划分网格时,为达到高效且不影响计算精确性要求,决定采用混合离散网格划分方式。计算域总体选用六面体网格,建筑物周围的小片区域选用四面体网格,在离建筑物较远的边缘区域选用较为稀疏的网格,减小网格数量。由于流体易在建筑物细部形状的拐角区处产生分离,对计算结果影响较大,为了正确模拟拐角部位分离特性,在建筑物表面采用10层正交网格从而准确的描述建筑物的复杂边界。不同风向角下划分的网格的最小尺寸是0.1 m,网格数量总数约为200万左右。0°风向对应的计算域网格分块见图4和图5。

图4外部流场网格
Fig.4Grid distributions of wind field

图5建筑附近网格
Fig.5Grid distributions near the building surfaces
2.3边界条件的设定
首先分析高层建筑在定常边界条件下的风场特性,选用雷诺平均数值模拟方法(RANS)进行数值模拟。

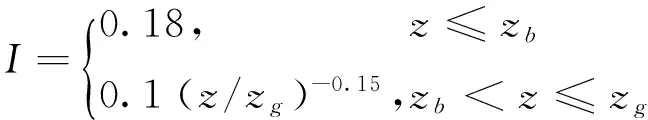
(6)
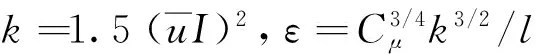
②出口条件:选取充分发展出流边界条件。
③流域顶部及两侧:选用自由滑移的壁面。
④建筑物表面和地面:选用无滑移的壁面条件。
非定常数值模拟入口采用谱合成(Spectral Synthesizer)法,在考虑脉动风场的功率谱、相关性、风剖面等参数的前提下,生成满足目标风场湍流特性的随机序列数,准确的模拟大涡模拟入口处的脉动信息。风速谱合成法[14]是先对目标谱做傅里叶变换(FFT)后求和来模拟点的脉动风速。脉动风速的公式:
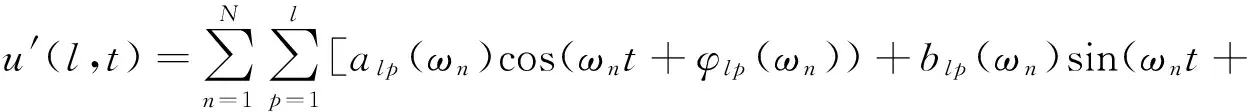
(7)

入口风速时程的平均风速剖面采用指数分布风剖面公式,与定常数值模拟的参数一致。将平均风速条件和脉动风速相加即为非定常风速入口。
u(y,t)=U(y)+u′(y,t),
(8)
其中:u为风速,U是平均风速,u′为脉动风速。
采用大涡模拟A类风场,在计算域进口处沿高度方向设置监控点,平均风速度剖面和湍流强度剖面见图6。
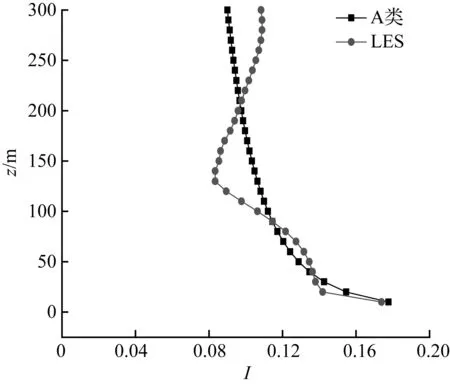

图6 入口风速、湍流强度剖面
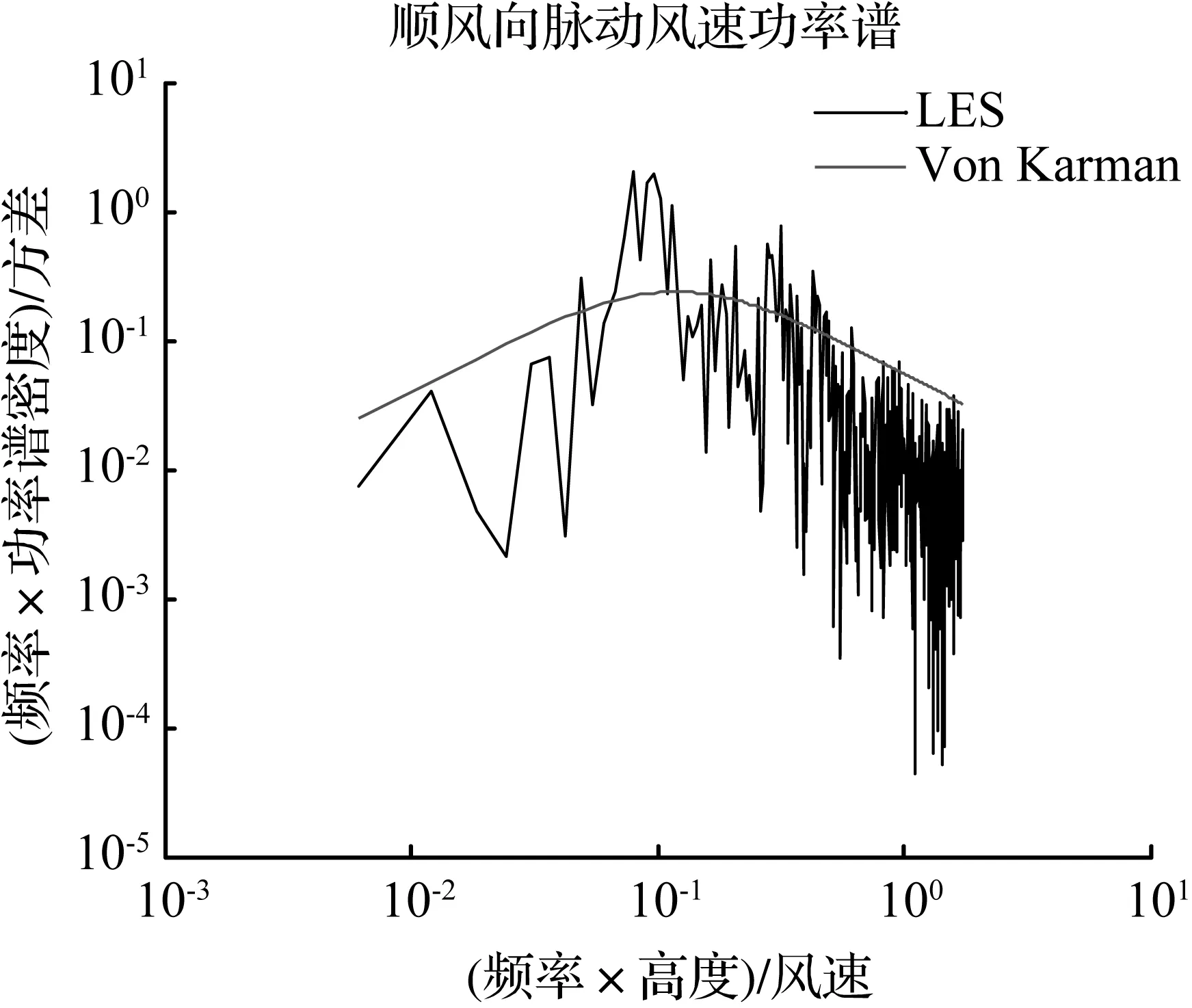
图7 大涡模拟的风速功率谱Fig.7 Spectrum generated by LES
大涡模拟的风速谱及Von Karman谱见图7,可知大涡模拟的风速谱和Von Karman谱基本吻合,即入口边界处的湍流脉动特性能够真实地模拟大气边界层的脉动特性。
在大涡模拟中,亚格子模型选用Smagorinsky-Lilly模型,近壁面的绕流特征选择非平衡壁面函数模拟。选用3D单精度、分离式求解器, 气体模型采用不可压缩的常密度空气,选择二阶迎风格式模拟对流项的离散, 选择SIMPLEC 算法求解速度和压力场。初场计算选取RANS湍流模型的定常计算结果,并且进行瞬态化处理,选取的非定常的计算时间步长为0.005 s,全部控制方程的相对迭代残差值都小于1×10-4, 并且建筑物表面的压力系数不再发生改变时,可认定为流场达到了稳态,迭代计算完成。
3 数值模拟结果及其同风洞试验结果的比较与分析
3.1数值模拟获得的建筑物顶面流速及流线
图8为0°和90°时的流线图的风速仪所在的ZX平面的风速矢量图,由图8发现,流线在建筑顶部和两侧都出现了明显的分离绕流现象,由于绕流,建筑顶面都出现的局部风速较来流增大的情况。同时可以看出由于绕流,在距离建筑顶面较低的位置风速明显会下降,即在距离建筑顶面较低区域处于绕流的下部,风速会较来流明显减小。

(a) 0°风向角

(b) 90°风向角
图8风速矢量图
Fig.8Figure of streamline and velocity contour
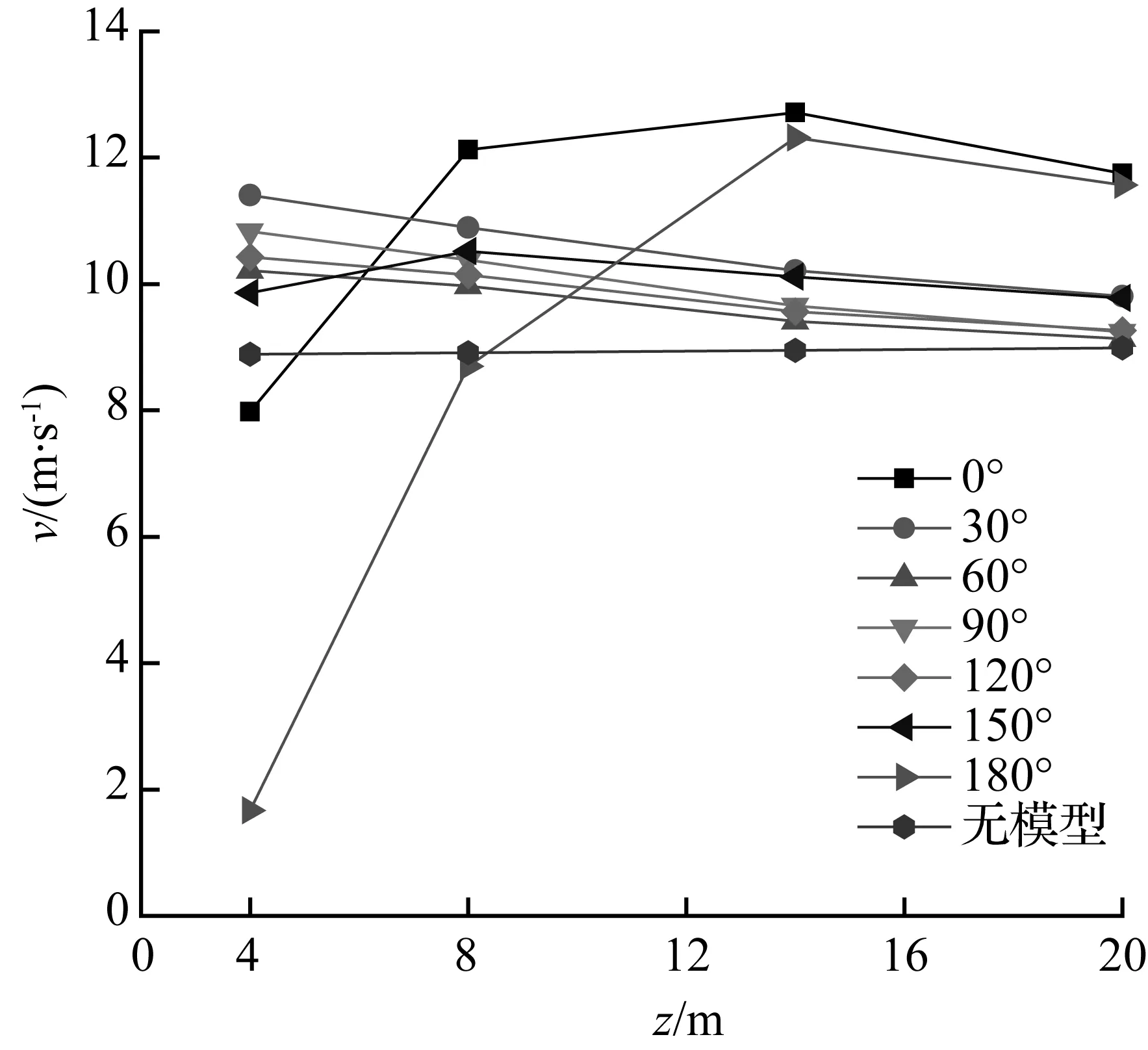
图9 各风向角下测点不同高度的风速值Fig.9 Measuring point velocity value at vary wind angle
由图9可以发现,当风速仪位于来流方向离建筑边缘较近的部位时,如风向角为60°、90°、120°时,数值模拟下的风速值接近理论值,绕流的影响较小;当风速仪位于来流方向离建筑边缘较远的部位时,如风向角为0°、180°时,风速随高度变化较大,绕流的影响较大,此时风速仪应架设在较高部位。
3.2数值模拟结果与风洞试验结果的对比
风洞试验将风场调试好后先测量出有模型时其位置A处实际为4、8、14和20 m高度处的风速。然后测量位置A处相应高度无模型,即未受建筑影响的来流相应高度风速,下文中的高度为风速仪实际距离建筑顶面的高度。选取了离建筑物顶面14 m和20 m处的不同风向角下风洞试验和数值模拟的风速值分析,从图10和图11中得知随着风向角的增大,数值模拟下的风速有先减小后逐渐增大的趋势,而且与风洞试验随风向角的变化一致;并随着高度增加两种情况下风速差值减小,可以认为数值模拟和风洞试验吻合较好,都能反应来流受建筑本身影响后屋顶风场的扰动情况。
由图11可以看出,在离建筑物顶面20 m高度处,当风速仪位于来流方向离建筑边缘较远的部位时,如风向角为60°、90°、120°时,数值模拟和风洞试验的风速值都与无模型工况的风速值接近,绕流的影响较小;当风速仪位于来流方向离建筑边缘较远的部位时,如风向角为0°、180°时,风速随高度变化较大,绕流的影响较大,开展实测研究时风速仪应架设在较高部位。

图10屋顶14 m处风洞试验和数值模拟的风速
Fig.10The velocity of wind tunnel test and numerical simulation at 14 m

图11屋顶20 m处风洞试验和数值模拟的风速
Fig.11The velocity of wind tunnel test and numerical simulation at 20 m
3.3建筑物自身影响
为了方便风洞试验和数值模拟对比,采用受建筑模型影响后相应高度风速与来流相应高度处风速增大系数C表示,具体计算公式如下;

(9)

图12 风洞试验的C值Fig.12 C value of wind tunnel test
其中v为受建筑模型影响时相应高度的风速,v0为无模型时的相应高度的风速即未受建筑影响的来流风速。由图12可知,在4 m到20 m这段范围内,其增大系数C都出现了先增大后减小的情况,这可能是来流受建筑影响出现绕流引起的。值得注意的是风洞试验系数C在高度较低时出现了负值,说明屋顶风场在离建筑物顶面附近处风速出现了比来流小的情况。任何角度下,随着距离建筑顶面的距离的增大,位置A处的风速将会逐渐与来流风速接近,即随着距离的增大,建筑对来流的影响会下降。
系数C的数值上看,在60°到120°风向角范围内,系数C的绝对值都不会大于5%,说明在这种风向角范围内,该位置处建筑顶面风速与来流不会产生较大的差异;而在0°和180°时,风速仪距离来流方向建筑边缘较远,系数C的绝对值基本在10%以上,即使在距离建筑顶面20 m时,系数C也在10%左右,所以在架设风速仪时应注意来流风向,减少测量过程中建筑物的阻扰对来流风速的影响。
3.4大涡模拟分析屋顶风场
在建筑顶部实测点A处沿高度方向布置40个测点,共监测建筑顶面至40 m高度的风速时程。对比图13和图14可知,由于建筑物自身的干扰作用,距离建筑顶部高度较近处平均风速较小;随高度逐渐增加测点的平均风速值先变大后减小。当距建筑顶面的高度大于30 m时,建筑物自身对来流的平均风速值的影响较小。风向角为0°和180°时,由于建筑局部外形影响,距离建筑顶部高度较近处风速变化较大,随着高度增加风速变化逐渐减小;定常模拟结果和大涡模拟的平均风速计算结果一致。
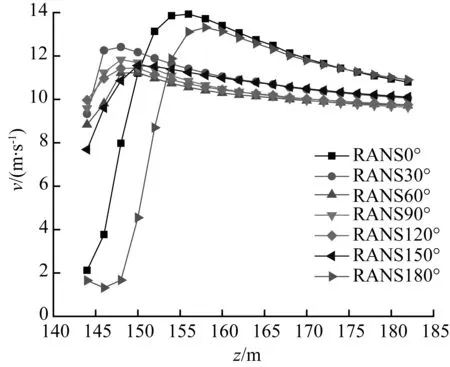
图13定常模拟A点平均风速
Fig.13Mean wind velocity of steady state simulation at pointA
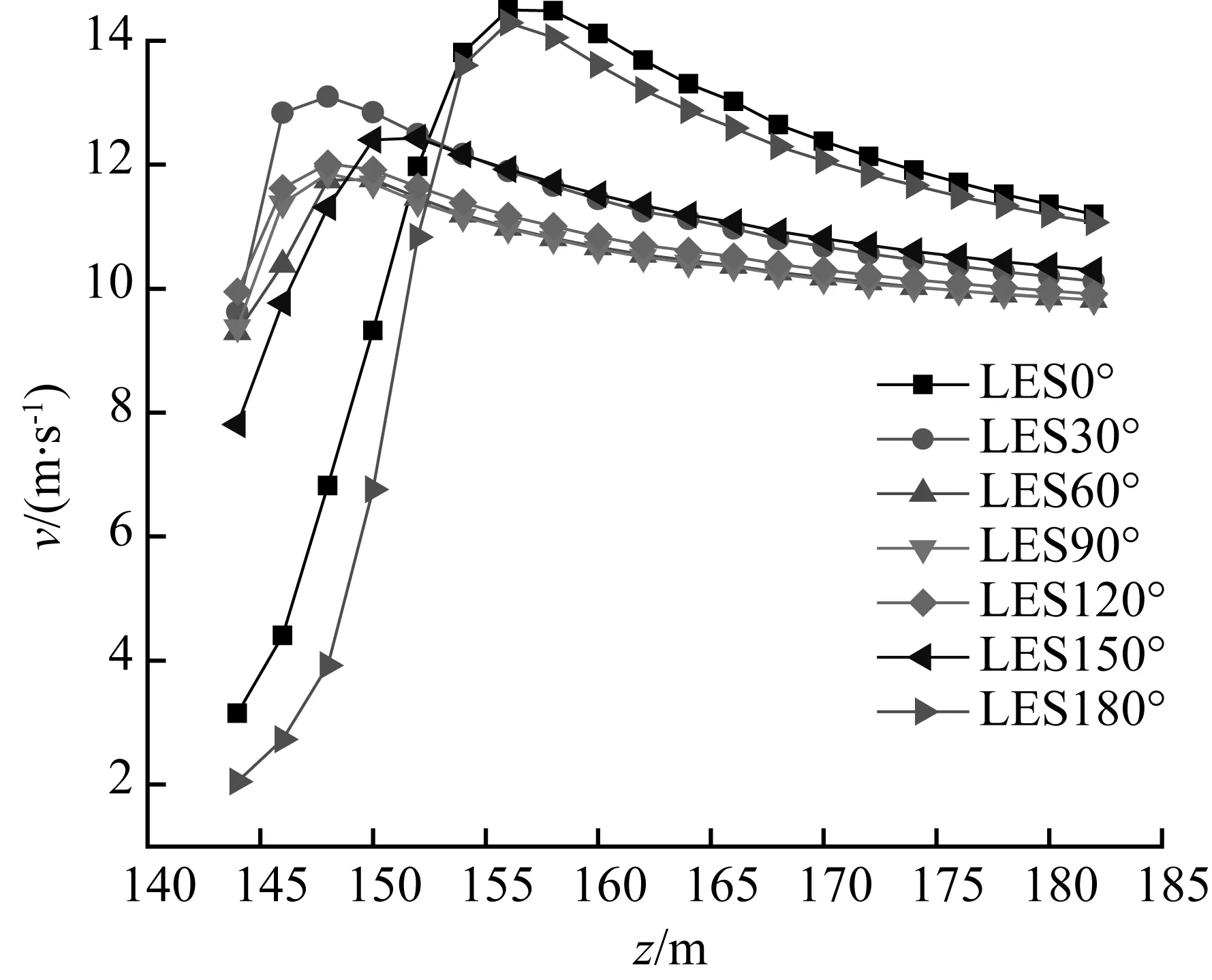
图14大涡模拟A点平均风速
Fig.14Mean wind velocity by LES at pointA
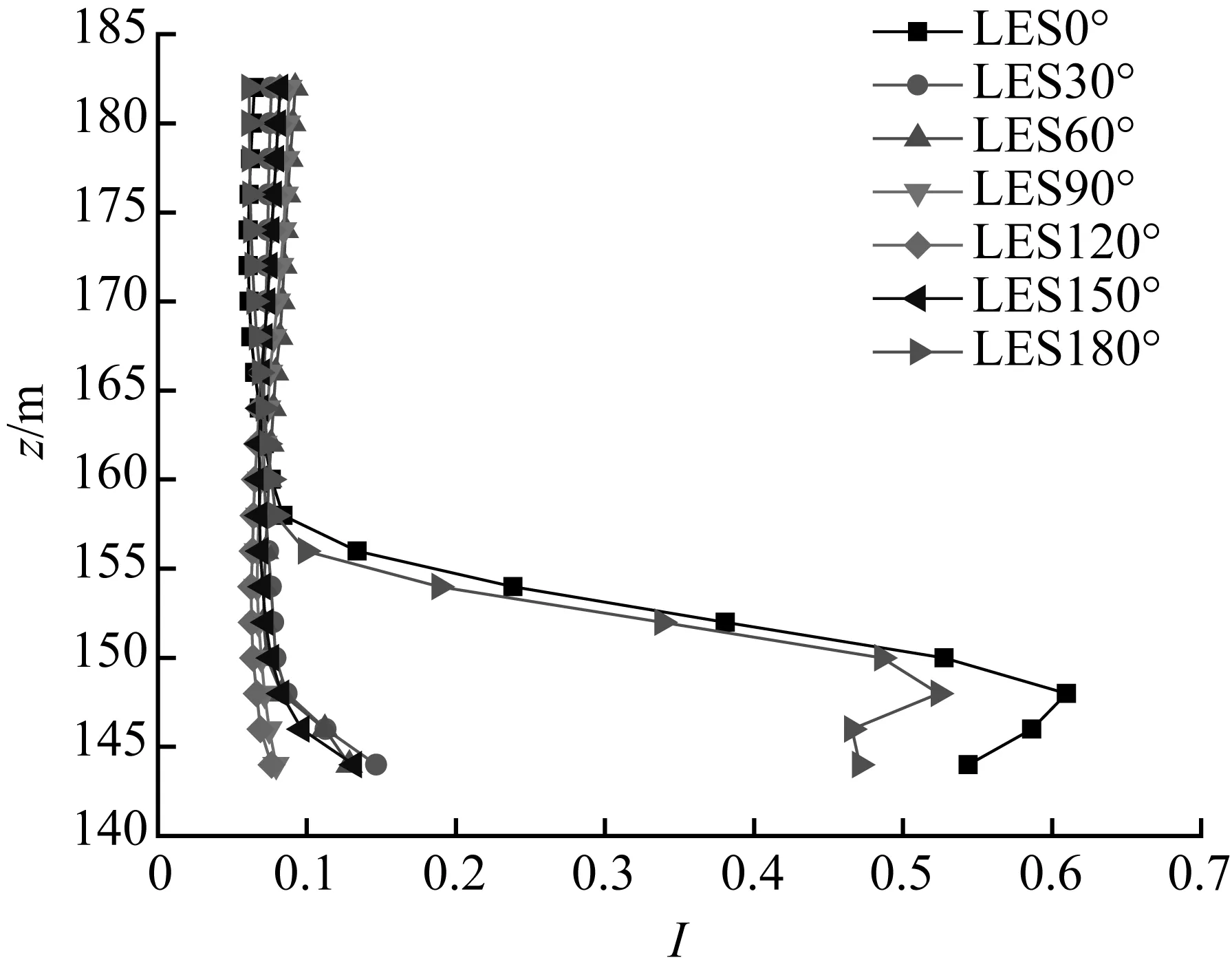
图15 建筑顶部A点湍流强度Fig.15 Turbulence intensity at point A
由图15可看出,距离建筑顶部高度较近处湍流强度较大;随高度增加,湍流强度逐渐减小。风向角为0°和180°时,由于建筑局部高度的影响,距离建筑顶部高度较近处湍流强度较大,随高度增加,湍流强度逐渐减小。
4 结 语
本文通过数值模拟和风洞试验来找到高层建筑风场实测时风速仪架设的最佳位置和高度,并期待为相似建筑的现场实测提供参考,主要得出了以下结论:
①数值模拟和风洞试验的结果能够较好的吻合,说明数值模拟和风洞试验都能用于研究建筑屋顶部风场受其本身影响。
②当风速仪安装位置位于来流方向建筑边缘处时,只要将风速仪安装在距离建筑顶面14 m以上,就能获得与来流相同高度较为接近的风速。
③当风速仪安装位置距离来流风向建筑边缘较远时,受建筑物自身影响,测得的风速与来流风速有较大的差异。应考虑来流风向角的影响,在风向角为60°到120°范围内,可以降低建筑物自身对来流的作用,减少对屋顶风场的影响。
④由于建筑物顶部测点高度增大,顶部风场的平均风速值先变大后减小;而湍流强度在建筑物顶部附近较大,随高度增加逐渐减小,建筑物对风场的影响逐渐减弱。
[1]李正农, 罗叠峰, 史文海,等.台风“鲇鱼”作用下厦门沿海某超高层建筑风压特性的风洞试验与现场实测对比研究[J]. 建筑结构学报, 2012, 33(1):10-17.
[2]罗叠峰,李正农,回忆.海边三栋相邻高层建筑顶部台风风场实测分析[J]. 建筑结构学报, 2014,35(12):133-139.
[3]申建红,李春祥.强风作用下超高层建筑风场特性的实测研究[J]. 振动与冲击, 2010, 29(5):62-68.
[4]李正农,王尚雨.某体育馆屋盖结构风致响应及风振系数研究[J]. 广西大学学报(自然科学版), 2016,41(1):29-35.
[5]HE WK, YUAN W B. Numerical simulation of wind field characteristics around two adjacent high-rise buildings[C]//Proceedings of the 3rd Conference on Computational Mechannics (CCM 2014). Beijing: Engineering Information Institute、 Open Access Library、 Scientific Research Publishing,2014.
[6]GUIRGUIS N M, HASSAN M A, SHAALAN M R, et al.Construction and testing of a wind tunnel for in-door investigation of environmental effects on buildings[J]. Renewable Energy, 1996, 8(1-4):186-189.
[7]聂少锋,周绪红,周天华,等.CAARC标准高层建筑三维钝体绕流风场数值模拟[J]. 土木建筑与环境工程, 2009, 31(6):40-46.
[8]张冬兵,梁枢果,陈寅,等.高层建筑风场的数值模拟和风洞试验结果比较[J]. 武汉理工大学学报, 2011,33(4):104-108.
[9]顾明,赵雅丽,黄强,等.低层房屋屋面平均风压的风洞试验和数值模拟[J]. 空气动力学学报, 2010, 28(1):82-87.
[10]杨伟,顾明.高层建筑三维定常风场数值模拟[J]. 同济大学学报(自然科学版), 2003, 31(6):647-651.
[11]HUANG S H, LI Q S, WU J R.A general inflow turbulence generator for large eddy simulation[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2010, 10(10-11):600-617.
[12]卢春玲,李秋胜,黄生洪,等.大跨度复杂屋盖结构风荷载的大涡模拟[J]. 土木工程学报,2011(1):1-10.
[13]朱伟亮.基于大涡模拟的CFD入口条件及脉动风压模拟研究[D]. 北京:北京交通大学, 2011.
[14]沈炼,韩艳,蔡春声,等.基于谐波合成法的大涡模拟脉动风场生成方法研究[J]. 湖南大学学报(自然科学版),2015,42(11):64-71.
(责任编辑唐汉民梁碧芬)
Influence of building roof on its wind field
LI Zheng-nong, GENG Yan
(Key Laboratory of Building Safety and Energy Efficiency of the China Ministry of Education, Hunan University,Changsha 410082, China)
Currently, typhoon fields of high-rise buildings are mainly measured by the anemometers erected on the roofs of the buildings. However, the wind field on the roof of high-rise building is affected by the building itself, and the influence changes when the location of anemometer or the direction of incoming flow are different. Numerical simulation and wind tunnel test are used to simulate the wind filed of atmospheric boundary layer in site and to analyze nearby wind field influenced by the building itself, and the agreement of the wind fields on the building’s roof obtained by the two means hereinbefore are also analyzed. It is concluded that the effect of wind speed on the roof of high-rise buildings is gradually decreased with the height. The height and best location of the anemometer are confirmed. By the means of spectrum synthesis method which aims at creating an entrance condition, large eddy simulation (LES) is carried out to explore the effect of high-rise building on its own wind field and compare the differences with and without incoming wind flow, which acts as a reference for similar buildings in the aspect of field measurement.
high-rise buildings; wind field; wind tunnel test; numerical simulation
2016-04-20;
2016-05-25
国家自然科学基金资助项目(91215302,51478179)
李正农(1962—),男,湖北武汉人,湖南大学教授,博士生导师;E-mail:zhn88@263.net。
10.13624/j.cnki.issn.1001-7445.2016.0930
TU317
A
1001-7445(2016)04-0930-09
引文格式:李正农,耿燕.建筑物对屋顶风场的影响[J].广西大学学报(自然科学版),2016,41(4):930-938.
