基础隔震框架结构动力时程分析的精细积分法
2016-08-30胡启平王丽娟
胡启平,王丽娟
(1.河北工程大学土木工程学院, 河北邯郸056038; 2.河北旅游职业学院, 河北承德067000)
基础隔震框架结构动力时程分析的精细积分法
胡启平1,王丽娟2
(1.河北工程大学土木工程学院, 河北邯郸056038; 2.河北旅游职业学院, 河北承德067000)
为了求得基础隔震框架结构抗震性能的高精度数值解,基于层剪切模型建立了结构的动力方程。引入对偶变量,导出动力时程分析的哈密顿正则方程,应用初值问题的精细积分法求得数值解;最后应用MATLAB语言编制程序对一应用橡胶垫基础的6层框架结构进行多遇地震作用下的动力时程分析。计算结果表明,在相同的地震波作用下,相对于传统抗震结构,基础隔震结构的层间位移减少了60%,速度和加速度减少了30%,顶层最大位移减少了15%。由此可见,基础隔震结构具有优良的抗震性能。该方法是求解基础隔震框架结构动力时程分析的新方法,计算数据精度高、可靠性好。
哈密顿正则方程;精细积分法;基础隔震;MATLAB语言;动力时程分析
地震是不可预测的自然灾害,给人类生命和财产安全带来严重威胁。传统的弹塑性抗震设计方法利用结构构件的强度和弹塑性变形,在保证人身安全的同时并不能充分满足工程的实际需要。在这种背景下,基础隔震技术[1-4]迅速发展起来。其主要减震原理是在基础顶部与结构底部之间设置隔震层,使上部结构与基础隔离开来[5]。这样,在地震动过程当中,隔震层的变形吸收和消耗了大量的地震能量,同时延长结构体系的自振周期[6]、增大阻尼,从而有效的减少了地震反应。
经过国内外学者的不断努力,基础隔震技术在实验研究与工程应用中都取得了很大的进步。Jenn等[7]对基础隔震结构进行了振动台实验,程晓杰、方咏[8]和徐丽佳[9]利用有限元分析软件SAP2000对基础隔震结构进行了分析,结果表明基础隔震结构减震效果明显。至今为止,我国已经建成隔震结构近400栋,覆盖了大部分抗震设防区。本文建立了基础隔震框架结构动力时程分析的哈密顿对偶求解体系,应用初值问题的精细积分法进行数值计算,给出了一套基础隔震结构动力时程分析的新方法。

图1 动力模型Fig.1 Dynamic model
1 基本理论
对于多层现绕钢筋混凝土框架隔震结构,其上部各层的层间刚度比较小,当地震来临时,应将其视为多质点结构进行计算分析。本文基于层剪切模型,各层质点的质量采用集中质量法计算,并将其集中于楼层标高处。隔震层的水平刚度为所有隔震垫水平刚度的总和。橡胶垫产生的水平恢复力与水平位移成正比,认为其竖向刚度远远大于其水平刚度,故在地震动过程中只考虑水平变形。这种多质点平动体系的动力模型如图1所示。在分析过程中忽略隔震层顶部楼板的变形,考虑刚性楼板将各平面抗侧力结构连接在一起共同承受侧向水平荷载。假定地震水平合力作用线通过框架结构的刚度中心,因此不考虑结构在水平荷载作用下绕竖轴的扭转。
设框架结构共有n层,第i层的层间刚度为kj。将框架结构沿高度按楼层分为若干单元,记每层单元刚度矩阵[10]为:
(1)
应用有限元法由单元刚度矩阵集成上部框架结构整体刚度矩阵K*:

(2)
本文采用多质点模型,每层质量取上下半层之和,并将各层质量集中于楼层标高处,得上部框架结构的质量矩阵为:
M*=diag(M1,M2,…,MN)。
(3)
上部框架结构阻尼采用瑞雷阻尼,其计算公式为:
C*=a0M*+a1K*,
(4)
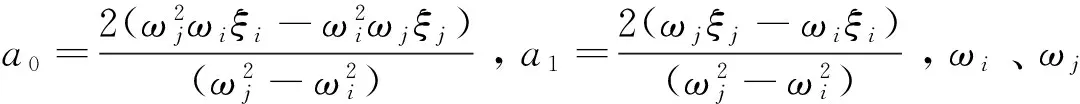
隔震层及上部框架结构运动方程分别为:

(5)
式中,x=[x1,x2,…,xi,…,xn]T为上部结构相对结构底层水平位移;M*,C*,K*分别为上部框架结构的质量矩阵、阻尼矩阵和刚度矩阵;M0,C0,K0分别为隔震层的质量、阻尼和刚度[11-12];Mi为框架结构第i层集中质量;Xg为地面地震位移;X0为结构底层与基础面之间的水平相对位移;I=[1,1,…,1]T为单位向量。
2 运动方程的整合
由式(5)隔震结构体系的运动方程,并令Xi=X0+xi(i=1,2,3,…,N),将公式整理合并得整体结构的运动方程为:

(6)

M=diag(M0,M1,M2,…,MN),
(7)
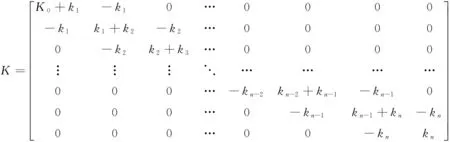
(8)

(9)
3 哈密顿正则方程
基础隔震结构整体动力方程表达式为:

(10)

(11)

精细积分法是求解线性定常微分方程的一种高精度数值解法,矩阵H为哈密顿矩阵,它是一个辛矩阵。哈密顿正则方程采用了状态空间的描述,引入对偶变量将二阶常微分方程组降为一阶常微分方程组。因此,本文采用精细积分法(即直接积分法)来求解动力方程式。
取地震波时间间隔η,并将荷载作用时间按η分成若干段,即:
tk=kη,tk=tk-1+η,k=1,2,…,n
(12)
(13)
综上可得,式(11)的解可以表示为:
(14)

4 计算实例

图2 框架结构平面图Fig.2 Plan view of the frame structure
工程实例为一栋6层钢筋混凝土框架结构办公楼,其结构平面图如图2所示。楼高21.6 m,层高均为3.6 m,框架柱、主梁、次梁和楼板的截面尺寸分别为450 mm×450 mm、300 mm×600 mm、250 mm×500 mm、120 mm,选用C30混凝土。设防烈度为7度,设计抗震分组为第一组,场地类别为三类。每根柱子下设置一个叠层橡胶支座,选用型号GZY300并根据《建筑抗震设计规范》(GB50011-2010)选取,其参数如表1所示。
地震波采用后14 s南北向天津波,间隔为0.01 s,加速度峰值为145.8 mm/s2,并将加速度幅值调整到0.35 m/s2,在多遇地震下对结构进行分析。

表1 隔震支座参数Tab.1 Parameters of the laminated
对上述钢筋混凝土框架结构应用本文编制的MATLAB程序进行动力时程分析,得层间位移、速度、加速度值如表2所示。结构顶层速度、位移和加速度时程图如图3、图4、图5所示。

表2 时程分析计算结果Tab.2 The calculation results of time-procedure analysis
由表1可见:应用基础隔震结构的层间位移相对传统抗震结构减小明显,减小率在58%~62%之间,层间位移的大幅度减小可以有效的降低结构在地震过程中的损伤,从而增强了结构的抗震性能,可以更好的保证生命和财产的安全。应用基础隔震结构的速度和加速度相对于传统抗震结构大幅减少,减小率在30%左右,而且层数越高,减小率越大。这是因为在地震动过程中,隔震结构的柔性隔震层在吸收了大量的地震能量的同时,也阻隔了地震能量向上部结构的传递。
从顶层速度、位移和加速度时程曲线(如图3、图4、图5)可以看出,基础隔震结构相对于传统抗震结构的顶层最大速度、最大位移和最大加速度值分别由原来的0.46 m/s、0.07 m、2.31 m/s2降低到了0.31 m/s、0.06 m、1.40 m/s2,结构顶层的地震反应值的降低充分说明了基础隔震结构对结构的抗震性能有所提高。在地震动过程中可以更好的保证生命和财产的安全。

图3顶层速度时程曲线
Fig.3Top floor speed curve

图4顶层位移时程曲线
Fig.4Top floor displacement curve

图5 顶层加速度时程曲线
5 结 论
本文针对基础隔震框架结构在多遇地震下的动力时程分析问题给出了一套新的求解方法。应用哈密顿正则方程和精细积分法并编制相应的MATLAB语言程序对一栋6层钢筋混凝土结构进行了动力时程分析,计算结果表明:基础隔震结构相对于传统抗震结构的层间位移减少了60%,速度和加速度减少了30%,同时顶层的最大位移减少了15%,可见减震效果明显。这样在保证结构安全的同时,可以适当的降低钢筋混凝土框架结构的抗震要求,从而降低工程造价,并起到改善房屋使用功能的作用。
[1]文佳,魏世宏,朱浪涛.隔震技术原理及存在问题分析[J]. 重庆科技学院学报,2007,9(2):29-33.
[2]干洪,杨一振.建筑结构基础隔震应用研究[J]. 安徽工程大学学报,2011,26(1):1-4.
[3]黄东梅,李创第,陈俊忠.基础隔震结构基于反应谱的地震作用取值[J]. 西安建筑科技大学学报,2007,39(4):504-511.
[4]李创第,陈欧阳,葛新广.多层隔震结构近似实空间解耦及地震作用取值[J]. 广西大学学报(自然科学版),2013,38(4):787-794.
[5]岳宏亮,姚维盛,罗献燕.简析结构隔震技术的特点及适用性[J]. 广西大学学报(自然科学版),2007,32(3):80-82.
[6]衡敏涛,吴垠龙,董万慧.采用基础隔震技术的框架结构抗震性能分析[J]. 建筑结构,2012(S1):524-527.
[7]JENN S H, TING Y H.Experimental study of isolated building under triaxial ground excitations[J]. Journal of Structural Engineering, 2000,126:879-826.
[8]程晓杰,方咏.采用基础隔震的框架—剪力墙结构抗震性能分析[J]. 安徽建筑工业学院学报,2011,19(6):6-10.
[9]徐丽佳.采用基础隔震装置的钢筋混凝土框架结构的抗震性能分析[D]. 成都:西南交通大学,2013.
[10]胡启平,王倩倩.Timoshenko悬臂梁自振特性分析的新方法[J]. 河北工程大学学报,2013,30(4):1-3.
[11]MATSAGAR V A, JANGID R S.Influence of isolator characteristics on the response of base-isolated structures[J]. Engineering Structures,2004,6:1735-1749.
[12]CALIO I,MARLETTA M,VINCIPROVA F.Seismic response of multi-story building base-isolated by friction devices with restoring properties[J]. Computers and Structures,2003,81:2589-2599.
[13]胡启平,王颖.框剪结构动力时程分析的精细积分法[J]. 河北工程大学学报,2011,28(1):1-9.
[14]胡启平,王颖.筒中筒结构动力时程分析的精细积分法[J]. 湘潭大学自然科学学报,2011,33(2):38-41.
[15]汪梦浦,周锡元.结构动力方程的高斯精细时程积分法[J]. 工程力学,2004,21(4):13-16.
(责任编辑唐汉民梁健)
Precise integration method for dynamic time history analysis of base-isolation frame structures
HU Qi-ping1, WANG Li-juan2
(1.College of Civil Engineering, Hebei University of Engineering, Handan 056038, China;2.Hebei Tourism Vocational College, Chengde 067000,China)
Based on the story shear model, a dynamic equation of base-isolation frame structure is established for high-precision numerical solution of its seismic performance. Dual variables are introduced to derive the Hamiltonian canonical equation for the dynamic time history analysis. The precise integration method of initial value problems is applied to obtain the numerical solution. The MATLAB program is used to carry out the dynamic time history analysis of a rubber-base 6-story frame structure under earthquake excitation. According to the calculated results, under the same earthquake wave, compared with traditional seismic structures, the story displacement of the base-isolation structure is reduced by 60%, speed and accelerated speed are both reduced by 30%, and the maximum displacement of top story is reduced by 15%. Therefore, the base-isolation structure has excellent seismicity. It is a new method to solve the dynamic time history problem of isolation frame structures. And the data is precise and reliable.
Hamiltonian canonical equation;precise integration method; base isolation;MATLAB program;dynamic time history analysis
2016-03-21;
2016-06-06
河北省自然科学基金资助项目(E2011402057)
胡启平(1963-),男,安徽六安人,河北工程大学教授;E-mail:huqiping@hebeu.edu.cn。
10.13624/j.cnki.issn.1001-7445.2016.0939
TU352.1
A
1001-7445(2016)04-0939-06
引文格式:胡启平,王丽娟.基础隔震框架结构动力时程分析的精细积分法[J].广西大学学报(自然科学版),2016,41(4):939-944.
