方案设计题常见解法
2016-08-26汪国刚
文/汪国刚
方案设计题常见解法
文/汪国刚
方案设计题考查数学的应用意识,命题的背景材料广泛,考生施展才华的空间大.下面以2015年的中考题为例,把中考设计类题归类分析,供你复习时参考.
类型1 利用一次方程进行方案设计
例1(2015年齐齐哈尔卷)为了开展阳光体育活动,某班计划购买毽子和长绳两种体育用品,共花费35元,毽子单价3元,长绳单价5元,购买方案有().
A.1种B.2种C.3种D.4种
解析:设毽子买x个,长绳买y根,依据题意得3x+5y=35,
类型2 利用一元一次不等式进行方案设计

图1
例2(2015年台湾卷)图1为某餐厅的价目表,今日每份餐点价格均为价目表价格的九折.若恂恂今日在此餐厅点了橙汁鸡丁饭后想再点第二份餐点,且两份餐点的总花费不超过200元,则她的第二份餐点最多有几种选择?()
A.5B.7
C.9D.11
解析:设第二份餐点价格为x元,由题意,得(120+x)×0.9≤200,
故满足条件的餐点价有60元,70元,…,100元共9种选择.选C.
类型3 利用函数进行方案设计
例3(2015年北京卷)一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:

会员年卡类型A 类_ _ _ _ _ _ _ B 类_ _ _ _ _ _ _ C类办卡费用(元)5 0 2 0 0 4 0 0每次游泳收费(元)2 5 2 0 _ _ _ _ _ _ _ _ _ 1 5 _ _ _ _ _ _ _ _ _
例如,购买A类会员卡,一年内游泳20次,消费50+25×20=550元,若一年内在该游泳馆游泳的次数介于45~55次之间,则最省钱的方式为().
A.购买A类会员年卡B.购买B类会员年卡
C.购买C类会员年卡D.不购买会员年卡
解析:设一年内在该游泳馆游泳x(次),所花的费用为y(元).购买会员年卡三种消费情况分别是:yA=25x+50;yB=20x+200;yC=15x+400.
由于45<x<55,当x=50时,yA=25×50+50=1300,yB=20×50+200=1200,yC=15×50+400 =1150,不购买会员年卡,需花费50×30=1500元,
∴1500>1300>1200>1150,选C.
类型4 方程、不等式、函数与方案设计
例4(2015年泸州卷)某小区为了绿化环境,计划分两次购进A、B两种花草,第一次分别购进A、B两种花草30棵和15棵,共花费675元;第二次分别购进A、B两种花草12棵和5棵.两次共花费940元(两次购进的A、B两种花草价格均分别相同).
(1)A、B两种花草每棵的价格分别是多少元?
(2)若购买A、B两种花草共31棵,且B种花草的数量少于A种花草的数量的2倍,请你给出一种费用最省的方案,并求出该方案所需费用.

∴A种花草每棵的价格是20元,B种花草每棵的价格是5元.
(2)设购买A种花草的数量为m株,则B种花草的数量为(31-m)株,
∵B种花草的数量少于A种花草的数量的2倍,
∵m是正整数,∴m最小值=11.
设购买花草总费用为W,则W=20m+5(31-m)=15m+155,
∵k>0,∴W随m的减小而减小,
当m=11时,W最小值=15×11+155=320(元).
答:购进A种花草11株、B种20株,费用最省,最省费用是320元.
类型5 几何问题的方案设计
例5(2015年洛阳卷)某校七年级学生到野外活动,为了测量一池塘两端A、B的距离,甲、乙、丙三位同学分别设计如下几种方案:
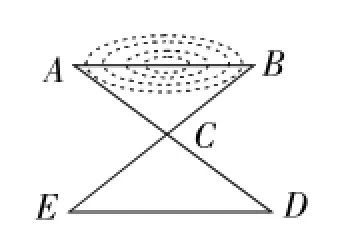
图1

图2

图3
甲:如图1,在平地取一个可直接到达A、B两点的C,连接AC、BC,并分别延长AC到D,BC到E,使DC=AC,EC=BC,最后测得DE的长即为A、B的距离;
乙:如图2,过点B作AB的垂线BF,在BF上取C、D两点,使BC=CD,过点D作BD的垂线DE,交AC的延长线于点E,测得DE的长即为A、B的距离;
丙:如图3,过点B作BD⊥AB,在AB的延长线上取一点C,使∠BDC=∠BDA,这时只要测出BC的长即为A、B的距离.
(1)以上三位同学的设计方案,可行的有_____;
(2)请你选择一种可行方案,并说明可行的理由.
解:(1)甲、乙、丙.
(2)答案不唯一,如选甲的方案.
理由是:∵DC=AC,EC=BC,∠ACB=∠DCE,
∴△ABC≅△DEC,所以AB=ED.
类型6 统计与概率的方案设计
例6(2015年宜宾卷)为进一步增强学生体质,我市从2016年起,中考体育测试将进行改革,实行必测项目和选测项目相结合的方式.必测项目有三项:立定跳远、坐位体前屈、跑步;选测项目:在篮球(记为X1)、排球(记为X2)、足球(记为X3)中任选一项.
(1)每位考生将有______种选择方案;
(2)用树状图或列表的方法求小颖和小华选择同种方案的概率.
解:(1)3.
(2)用树状图表示如下:
共有9种可能情况,同种方案的有3种,