多解问题归类解答
2016-08-26丁洁
文/丁洁
多解问题归类解答
文/丁洁

在中考试题中,多解问题是一类常见而重要的问题,解决这类问题要多角度、全方位、深层次地去思考.下面以2015年中考试题为例,对常见的多解问题加以归类解析,供你复习时参考.
一、由高的位置不同引起的多解
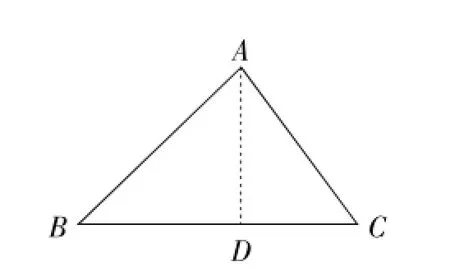
图1
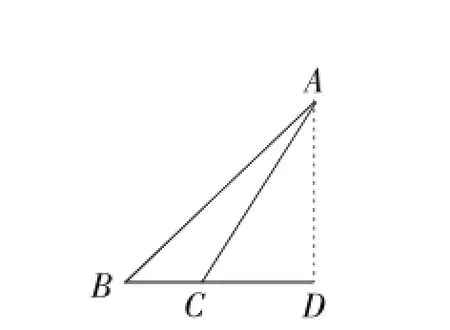
图2
A.7B.8C.8或17D.7或17
作AD⊥BC于点D,如图1.
(1)当高AD在△ABC内时,
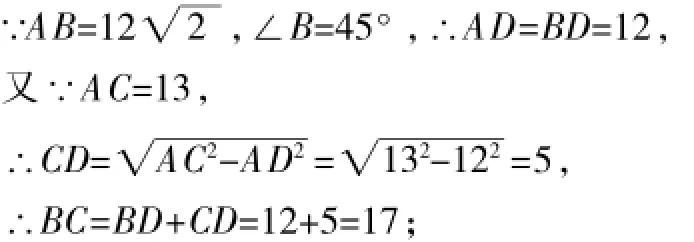
(2)当高AD在△ABC外时,如图2,BC=BD-CD=12-5=7.综合(1)、(2)可知,选D.
温馨小提示:三角形的高可在三角形内,也可在三角形上或三角形外,对于没有明确三角形高的位置的“涉高”问题,要注意分类讨论,谨防漏解.
二、由弦所对的弧引起的多解
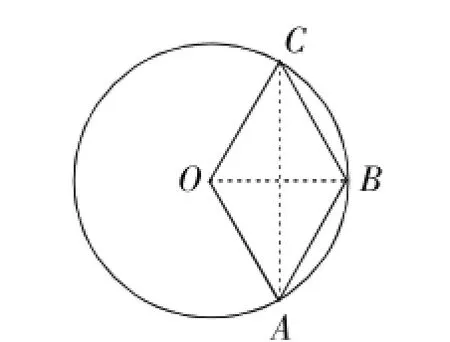
图3
例2(2015年泉州卷)在以O为圆心,3cm为半径的圆周上,依次有A、B、C三个点,若四边形OABC为菱形,则该菱形的边长等于______cm;弦AC所对的弧长等于_____cm.
解析:如图3,连接OB、AC,
∵四边形OABC为菱形,∴OA=AB=BC=OC.
∵⊙O的半径为3cm,∴OA=OC=3cm.
∵OA=OB=AB,∴△OAB为等边三角形,
∴∠AOB=60°,∴∠AOC=120°.
因此该菱形的边长等于3cm,弦AC所对的弧长等于2π或4πcm.
温馨小提示:在圆中,非直径的弦所对的弧有劣弧和优弧,要注意分类求解.
三、由绝对值的性质引起的多解
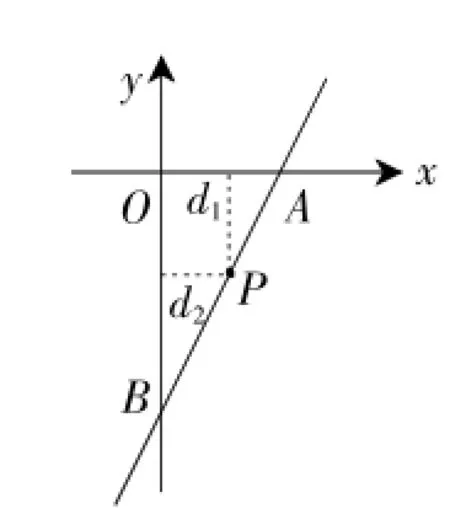
图4
例3(2015年泰州卷)已知一次函数y=2x-4的图像与x轴、y轴分别相交于点A、B,点P在该函数图像上,P到x轴、y轴的距离分别为d1、d2.
(1)当P为线段AB的中点时,求d1+d2的值;
(2)直接写出d1+d2的范围,并求当d1+d2=3时点P的坐标;
(3)若在线段AB上存在无数个P点,使d1+ad2=4(a为常数),求a的值.
解析:(1)令x=0得,y=-4,令y=0得,x=2,
所以OA=2,OB=4,故d1+d2=3.
(2)设P(m,2m-4),则d1+d2=|m|+|2m-4|.
当m>2时,d1+d2=m+2m-4=3,解得m=,此时P(1,);
当0≤m≤2时,d1+d2=m+4-2m=4-m=3,解得m=1,此时P(21,-2);
当m<0时,d1+d2=-m+4-2m=4-3m=3,解得m=,舍去.
(3)由已知得,|2m-4|+a|m|=4,当a=2,0≤m≤2时,都符合要求,故a=2.
温馨小提示:遇到含有绝对值的问题,需去掉绝对值符号,这就要根据绝对值的性质进行分类求解,从而得到多解.
四、由等腰三角形腰的不确定引起的多解
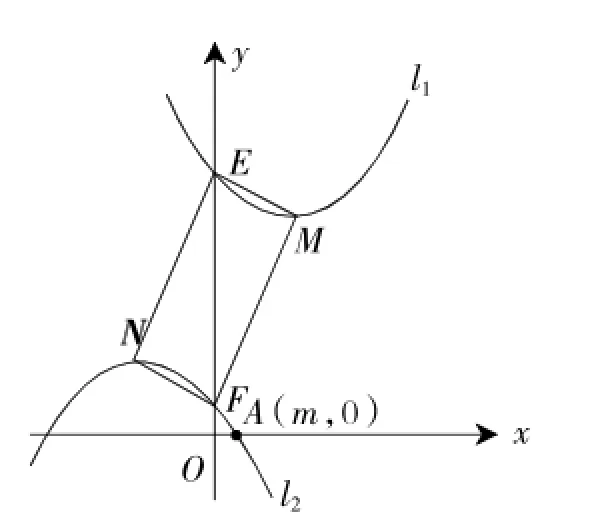
图5
例 4 (2015年南昌卷)如图5,已知二次函数l1:y= ax2-2ax+a+3(a>0)和二次函数l2:y=-a(x+1)2+1(a>0)图像的顶点分别为M、N,与y轴分别交于点E、F.
(1)函数:y=ax2-2ax+a+3(a>0)的最小值为______;当二次函数l1,l2的y的值都随着x的增大而减小时,x的取值范围是_____;
(2)当EF=MN时,求a的值,并判断四边形ENFM的形状(直接写出结论,不必证明);
(3)若二次函数l2的图像与x轴的右交点为A(m,0),当△AMN为等腰三角形时,求方程-a(x+1)2+1=0的解.
解析:(1)3;-1<x<1.
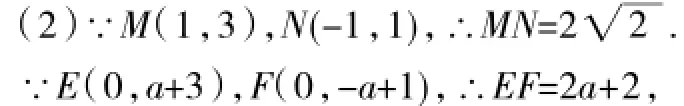
∴m1=-1,m2=--1(舍去);
∵抛物线y=-a(x+1)2+1的对称轴为x=-1,
∴方程-a(x+1)2+1=0的解为x1=2,x2=-4,x3=-1,x4=--1.
温馨小提示:在等腰三角形中,腰与底的不确定引起的多解是中考命题的热点,要求出所有答案,需要确定分类标准.
五、由对称性引起的多解
例5(2015年扬州卷)如图6,已知⊙O的直径AB=12,AC是⊙O的弦,过点C作⊙O的切线交BA的延长线于点P,连接BC.
(1)求证:∠PCA=∠B;
(2)已知∠P=40°,点Q在优弧ABC上,从点A开始逆时针运动到点C停止(点Q与点C不重合),当△ABQ与△ABC的面积相等时,求动点Q所经过的弧长.
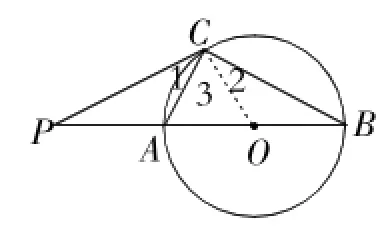
图6
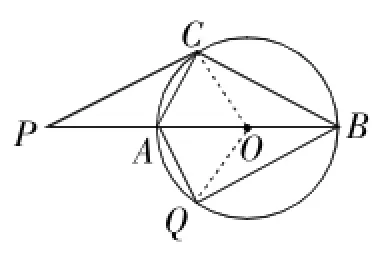
图7
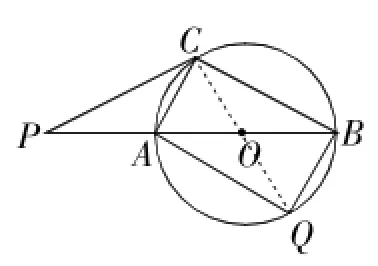
图8
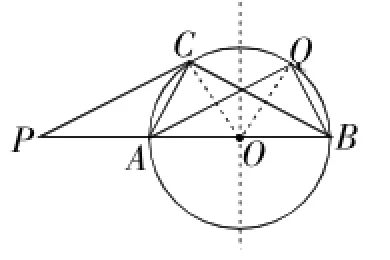
图9
解析:(1)如图6,连接OC.
∵AB是⊙O的直径,∴∠ACB=∠2+∠3=90°.
∵PC是⊙O的切线,∴OC⊥PC,
∴∠PCO=∠1+∠3=90°,∴∠1=∠2.
∵OC=OB,∴∠2=∠B,
∴∠1=∠B,即∠PCA=∠B.
(2)∵∠P=40°,∴∠POC=50°.
∵AB=12,∴AO=6.
当△ABQ与△ABC的面积相等时,动点Q在优弧ABC上有三个位置:
①如图7,点C关于AB的对称点,由轴对称性知,∠AOQ=∠POC=50°,
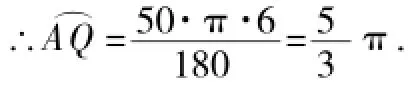
于如图8,点C关于点O的对称点,由中心对称性知,∠BOQ=∠POC=50°,
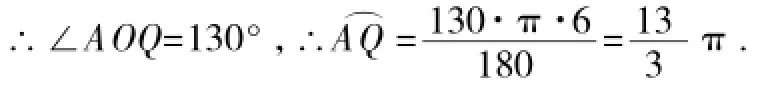
∴∠BOQ=∠POC=50°,∴∠AOQ=230°.
温馨小提示:由运动引起的多解是最常见的问题,若已知图形不完整需画出符合题意的所有图形,根据不同图形分别求解,得到所有的结论.
六、由操作过程的不确定引起的多解
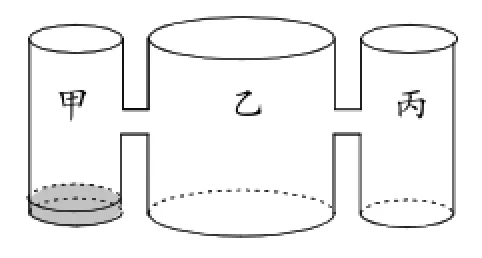
图10
例6(2015年绍兴卷)实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1∶2∶1,用两个相同管子在容器5cm高度处连通(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图10所示.若每分钟同时向乙和丙注入相同量的水,注水1分钟,乙的水位上升cm,则注入_____分钟的水量后,甲与乙的水位差是0.5cm.
解析:设注入t分钟的水量后,甲与乙的水位差是0.5cm,有三种情况:①当乙的水位低于甲的水位时;于甲的水位低于乙的水位,而甲的水位高1cm;③当甲的水位低于乙的水位时,乙的水位到达连通管的底部,甲的水位上升.
∵三个圆柱形的底面半径之比为1:2:1,
∴所以对应的底面圆的面积之比为1:4:1,
设注入t分钟的水量后,甲与乙的水位差是0.5cm.
③当甲的水位低于乙的水位时,乙的水位不断上升,到达连通管的底部后,乙的水流向甲,甲的水位开始上升,
温馨小提示:这是一道填空题的压轴题,有一定的难度.读懂题意,弄清甲与乙的水位差是0.5cm的所有情形,找出每一种情形下的等量关系,分别列出对应的一元一次方程求解.
