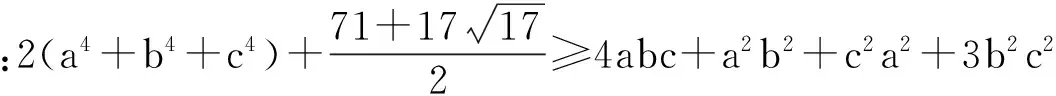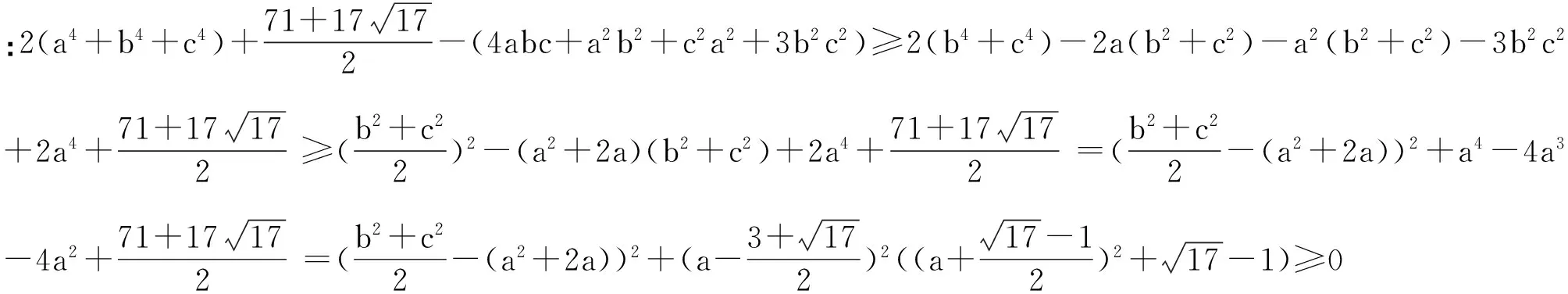恒等变形在不等式证明中的作用不容忽视——几道2016年国际数学奥林匹克不等式题的研讨

浙江省宁波市宁波外国语学校　(315121)

罗文静



恒等变形在不等式证明中的作用不容忽视
——几道2016年国际数学奥林匹克不等式题的研讨

浙江省宁波市宁波外国语学校(315121)

罗文静

在高中数学教学中，不少老师都认为不等式证明很难，难在哪呢？其实，不等式证明与代数式(当然还有三角式)的变形息息相关.当然，等式证明有目标，而不等式证明中对代数式朝什么方向变形以及怎样变形更多地依赖于解题者的观察、联想、分析、探索、判断和经验.在本文中，笔者借助于几道新近出炉的国际数学奥林匹克试题现身说法.

例1(2016年美国OMO数学奥林匹克)已知a,b,c,d是满足a+b+c+d=20和ab+bc+cd+da=16的实数，求abc+bcd+cda+dab的最大值.

注：本题求解中，代数式ab+bc+cd+da=(a+b)(c+d)，abc+bcd+cda+dab=ac(b+d)+bd(a+c)的恒等变形至关重要.

利用类似思想可解，已知 a,b,c,d 是满足 a+b+c+d=6和a2+b2+c2+d2=12的实数，求 abcd 的最大值.

注： 分分合合，整个解题就是不断的恒等变形；另外就是通过放缩实现消去b，剑指目标 6(c-a).

例3(2016年韩国数学奥林匹克)已知 x,y,z 是满足 x2+y2+z2=1 的实数，求 (x2-yz)(y2-zx)(z2-xy) 的最大值.

注：8(x2-yz)(y2-zx)(z2-xy)=4(xy+yz+zx)2-4(x+y+z)2(x2y2+y2z2+z2x2) ， 4(xy+yz+zx)2-(x+y+z)2(xy+yz+zx)2=1-(x+y+z)2(xy+yz+zx-1)2，这两个等式的证明成为本题求解的主干.

类似的竞赛题还有：已知x,y,z 是满足 x≥yz2,y≥zx2,z≥xy2的正数，求 (x-yz2)(y-zx2)(z-xy2) 的最大值.

例4(2016年IMO中国国家队选拔考试试题)求最小的正实数λ，使得对任意三个复数z1,z2,z3∈{z∈C||z|<1} ，若 z1+z2+z3=0 ，则|z1z2+z2z3+z3z1|2+|z1z2z3|2<λ.

注：此题看起来是不等式问题，其实不等式证明的技术用得微乎其微，繁复的恒等变形成为推理的主导。